Материал для подготовки к уроку по теме Повторение. Треугольники

УРОК 65.

Тема: Повторение. Треугольники.

Площадь треугольника.

,

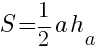здесь - произвольная сторона треугольника, - высота, опущенная на эту сторону.

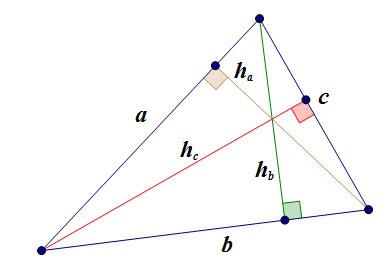рис. 1

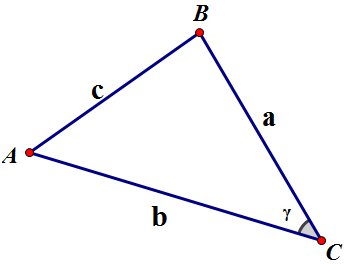рис. 2

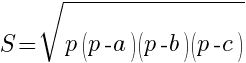
- формула Герона. Здесь - длины сторон треугольника, - полупериметр треугольника,

,

здесь - полупериметр треугольника, - радиус вписанной окружности.

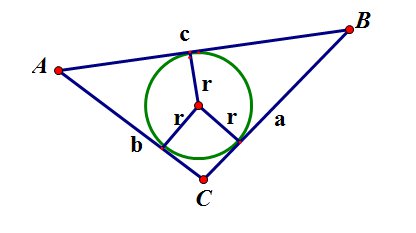рис. 3

,

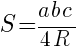здесь - длины сторон треугольника, - радиус описанной окружности.

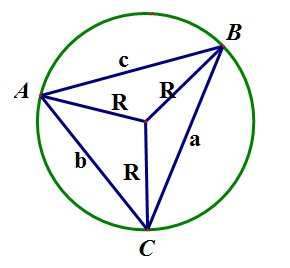рис. 4

Если на стороне треугольника взята точка, которая делит эту сторону в отношении m:n, то отрезок, соединяющий эту точку с вершиной противолежащего угла делит треугольник на два треугольника, площади которых относятся как m:n:

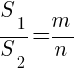
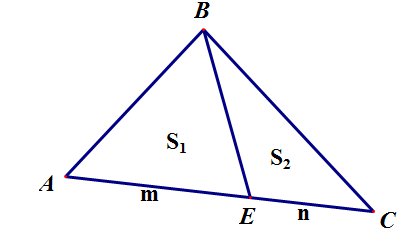рис. 5

Теорема. Отношение площадей подобных треугольников равно квадрату коэффициента подобия.

Медиана треугольника

- это отрезок, соединяющий вершину треугольника с серединой противоположной стороны.

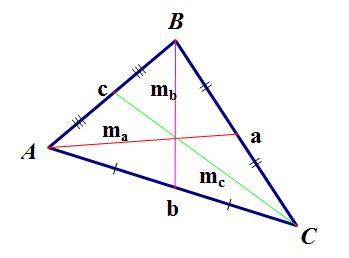рис. 6

Медианы треугольника пересекаются в одной точке и делятся точкой пересечения в отношении 2:1, считая от вершины.

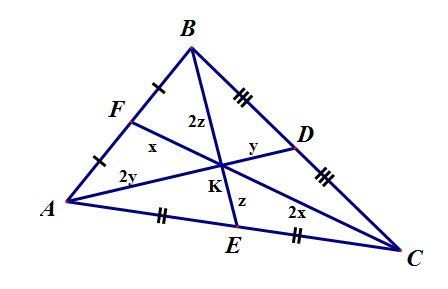рис. 7

Точка пересечения медиан правильного треугольника делит медиану на два отрезка, меньший из которых равен радиусу вписанной окружности, а больший - радиусу описанной окружности.

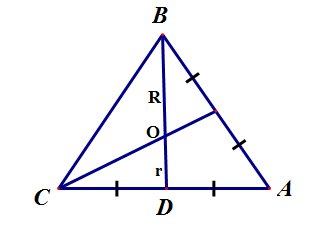рис.8

Длина медианы произвольного треугольника вычисляется по формуле:

,

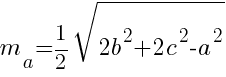здесь - медиана, проведенная к стороне , - длины сторон треугольника.

Биссектриса треугольника

- это отрезок биссектрисы любого угла треугольника, соединяющий вершину этого угла с противоположной стороной.

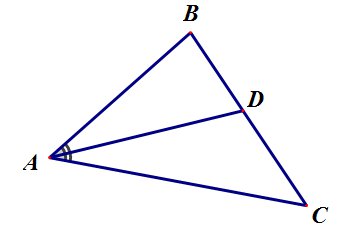рис.10

Биссектриса треугольника делит сторону на отрезки, пропорциональные прилежащим сторонам:

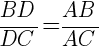
Биссектрисы треугольника пересекаются в одной точке, которая является центром вписанной окружности.

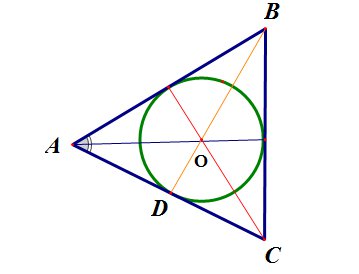рис. 11

Все точки биссектрисы угла равноудалены от сторон угла.

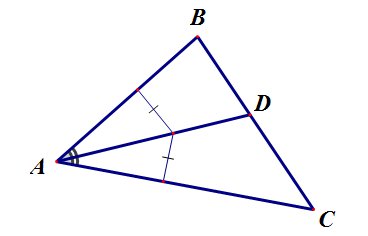рис.12

Высота треугольника

- это отрезок перпендикуляра, опущенный из вершины треугольника на противоположную сторону, или ее продолжение. В тупоугольном треугольнике высота, проведенная из вершины острого угла лежит вне треугольника.

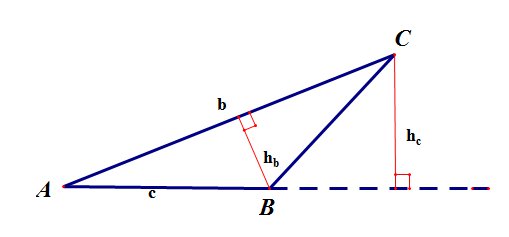рис. 13

Высоты треугольника пересекаются в одной точке, которая называется ортоцентром треугольника.

Чтобы найти высоту треугольника, проведенную к стороне , нужно любым доступным способом найти его площадь, а затем воспользоваться формулой:

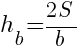
Центр окружности, описанной около треугольника, лежит в точке пересечения серединных перпендикуляров, проведенных к сторонам треугольника.

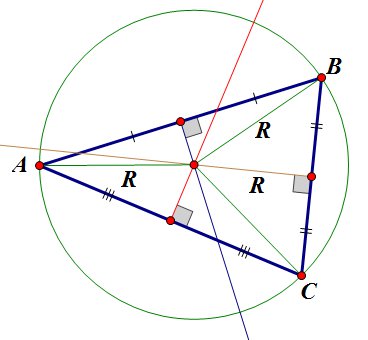рис.14

Радиус описанной окружности треугольника можно найти по таким формулам:

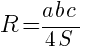
- здесь - длины сторон треугольника, - площадь треугольника.

,

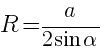где - длина стороны треугольника, - противолежащий угол. (Эта формула вытекает из теоремы синусов).

Неравенство треугольника

Каждая сторона треугольника меньше суммы и больше разности двух других.

Сумма длин любых двух сторон всегда больше длины третьей стороны:

Прямоугольный треугольник - это треугольник, один из углов которого равен 90°.

Сумма острых углов прямоугольного треугольника равна 90°.

Гипотенуза - это сторона, которая лежит против угла 90°. Гипотенуза является наибольшей стороной.

Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов:

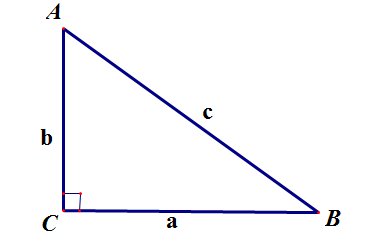рис. 15

Радиус окружности, вписанной в прямоугольный треугольник, равен

,

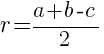здесь - радиус вписанной окружности, - катеты, - гипотенуза:

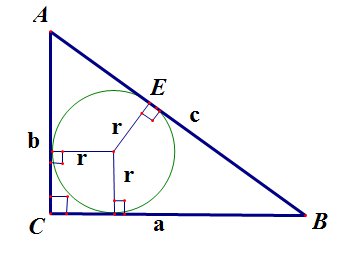рис.16

Центр окружности, описанной около прямоугольного треугольника лежит в середине гипотенузы:

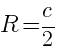
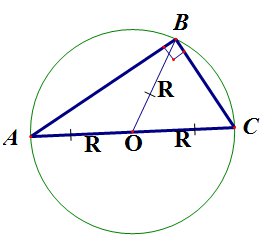рис.17

Медиана прямоугольного треугольника, проведенная к гипотенузе, равна половине гипотенузы.

Катет, лежащий против угла равен половине гипотенузы:

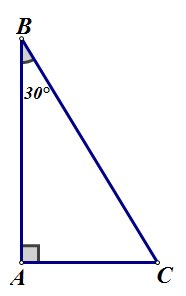
рис.18

Равнобедренный треугольник.

Биссектриса равнобедренного треугольника, проведенная к основанию является медианой и высотой.

В равнобедренном треугольнике углы при основании равны.

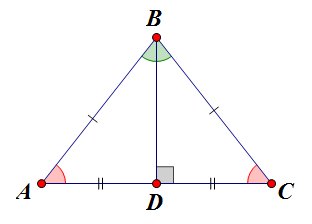рис. 19

- угол при вершине.

и - боковые стороны,

и - углы при основании.

- высота, биссектриса и медиана.

Внимание! Высота, биссектриса и медиана, проведенные к боковой стороне не совпадают.

Правильный треугольник (или равносторонний треугольник) - это треугольник, все стороны и углы которого равны между собой.

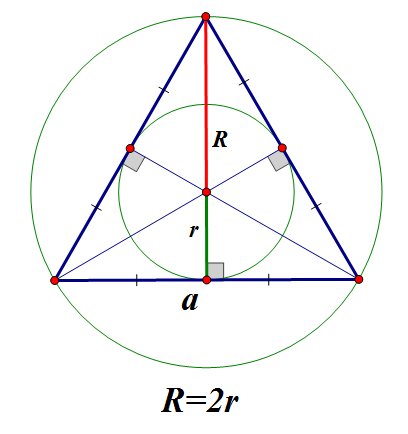рис. 19

Площадь правильного треугольника равна

,

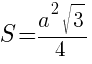где - длина стороны треугольника.

Центр окружности, вписанной в правильный треугольник, совпадает с центром окружности, описанной около правильного треугольника и лежит в точке пересечения медиан.

Точка пересечения медиан правильного треугольника делит медиану на два отрезка, меньший из которых равен радиусу вписанной окружности, а больший - радиусу описанной окружности.

Если один из углов равнобедренного треугольника равен 60°, то этот треугольник правильный.

Средняя линия треугольника - это отрезок, соединяющий середины двух сторон.

Средняя линия треугольника параллельна третьей стороне и равна ее половине: DE||AC, AC=2DE

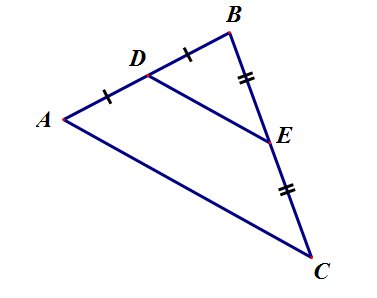рис. 20

Внешний угол треугольника - это угол, смежный какому либо углу треугольника.

Внешний угол треугольника равен сумме двух углов, не смежных с ним.

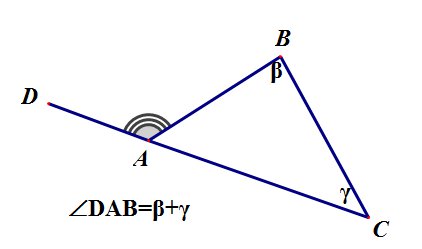рис. 21

Признаки равенства треугольников:

1. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

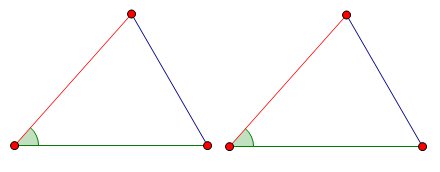рис. 22

2. Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

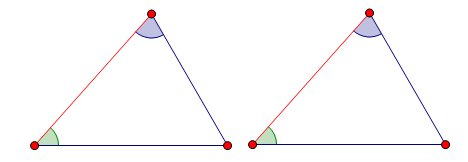рис.23

3 Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.

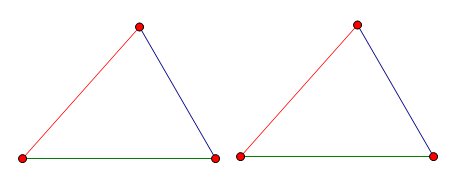рис.24

Важно: поскольку в прямоугольном треугольнике два угла заведомо равны, то для равенства двух прямоугольных треугольников требуется равенство всего двух элементов: двух сторон, или стороны и острого угла.

Признаки подобия треугольников:

1. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, и углы, заключенные между этими сторонами равны, то эти треугольники подобны.

2. Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то эти треугольники подобны.

3. Если два угла одного треугольника равны двум углам другого треугольника, то эти треугольники подобны.

Важно: в подобных треугольниках сходственные стороны лежат против равных углов.

Теорема Менелая

Пусть прямая пересекает треугольник , причем - точка ее пересечения со стороной , - точка ее пересечения со стороной , и - точка ее пересечения с продолжением стороны . Тогда

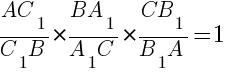
Выполните задания.