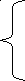
Министерство образования и науки Российской Федерации

Комитет образования и науки Курской области

ОБОУ СПО «Железногорский техникум сервиса и коммерции»

МЕТОДИЧЕСКАЯ РАЗРАБОТКА

ОТКРЫТОГО УРОКА ПО МАТЕМАТИКЕ

Тема:«Иррациональные уравнения»

Автор: Бурлыкина Эльвера Суфияновна,

Преподаватель математики ОБО СПО

«Железногорский техникум сервиса и коммерции»

г. Железногорск-2012 год

Пояснительная записка

к уроку математики по теме «Иррациональные уравнения».

Урок проводится для обучающихся II курса по программе для профессий социально - экономического профиля, владеющих основными методами решения уравнений, содержащих переменную под знаком корня. На изучение данной темы отводится 4 часа из 23 часов в разделе «Уравнения и неравенства». Решение таких уравнений всегда вызывают затруднения, в том числе и при выполнении экзаменационной работы. Актуальность выбранной темы заключается в том, что для получения удовлетворительной оценки достаточно выполнить обязательную часть письменной экзаменационной работы, которая содержит иррациональное уравнение и требует описания полного решения и ответа. На уроке много внимания уделено на повторение методов решения иррациональных уравнений, умению делать выборку корней с учетом ОДЗ, с оговоркой о потере и приобретении посторонних корней. Домашнее задание соответствует нормативным требованиям, дифференцировано, дано с комментарием.

ТЕМА УРОКА: «Иррациональные уравнения».

ЦЕЛИ УРОКА:

Образовательные: - обеспечить повторение, обобщение и систематизацию материала темы,

- расширить представление обучающихся о методах решения иррациональных уравнений.

Развивающие:

- способствовать развитию математического кругозора, мышления, речи, памяти.

Воспитательные:

- содействовать воспитанию интереса к математике, умению работать в команде, воспитывать чувство ответственности за собственную деятельность и деятельность всей группы.

ТИП УРОКА: учебное занятие по комплексному применению знаний и способов деятельности.

ВИД УРОКА: урок-практикум с интерактивным обеспечением.

ОБОРУДОВАНИЕ: интерактивная приставка «Mimio Teach», маркерная доска, карточки с кроссвордом, мультимедийный проектор, ноутбук, карточка «Таблица самооценки».

Этапы урока:

I. Организационный этап.

II. Определение темы урока.

III. Постановка цели урока. . IV. Актуализация ранее полученных знаний и умений. . V. Историческая справка о происхождении арифметического корня. . VI. Математическая эстафета. .VII. Решение иррациональных уравнений. VIII. Самостоятельная работа. . IX . Рефлексия.

Ход урока:

I. Организационный этап.

- проверка готовности группы к уроку;

- объявление порядка заполнения обучающимися «Таблицы самооценки».

II.Определение темы урока.

Преподаватель: Великий математик Блез Паскаль сказал: «Предмет математики настолько серьезен , что полезно не упускать случая сделать его немного занимательным». Я воспользуюсь таким случаем и объявление темы урока предоставлю вам. Для этого необходимо ответить на вопросы математического кроссворда. Тема урока состоит из словосочетания(из двух слов) . Ваша задача выделить это словосочетание.

(Обучающиеся самостоятельно решают математический кроссворд , затем коллективно формулируют тему урока ( Тема :«Иррациональные уравнения»),записывают в тетради. На экран проецируется слайд с названием темы).

III.Постановка цели урока.

Преподаватель: ( обращает внимание обучающихся на эпиграф урока):

Эпиграфом к сегодняшнему уроку я взяла высказывания великих людей, которые достигли высот и в математике тоже. И. Ньютон сказал: «При изучении наук примеры не менее поучительны , нежели теория», а

М. Ломоносов утверждал, что «примеры учат больше , чем теория».

Я думаю , мы согласимся с великими и перейдем к практике.

Преподаватель ставит перед обучающимися проблему : найти оптимальный

способ решения задачи (оптимальный способ решения задачи заключается

в составлении иррационального уравнения).

Задача: Строителям нужно изготовить рекламный щит прямоугольной

формы. Вычислите длину сторон прямоугольника, если длина его

диагонали равна 25 м, а периметр - 70 м. Найдите оптимальный

способ решения этой задачи.

Обучающиеся устно находят способы решения задачи.

Преподаватель: Перед вами стояла проблема: найти оптимальный способ

решения задачи. Вы предложили несколько способов. Но более оптимальный

- это решение с помощью иррационального уравнения.

Ваше домашнее задание:

а)решение задачи выполните разными способами, объясните устно, что решение задачи с помощью иррационального уравнения более оптимальное;

б)подберите из разных источников иррациональные уравнения, решаемые различными методами. Прошу обратить внимание на метод замены переменной.

Преподаватель: Определим цели нашей совместной работы, и каждый

поставит перед собой цель своей индивидуальной учебной деятельности на уроке.

Учащиеся обозначают цели учебной деятельности на уроке: - углубить знания об алгоритме решения иррациональных уравнений; - совершенствовать умения решения иррациональных уравнений; - рассмотреть типовые задачи из экзаменационных материалов; - проконтролировать и оценить свои знания по теме.

IV. Актуализация ранее полученных знаний и умений.

Преподаватель: 1.Сформулируйте определение иррациональных уравнений. ( Уравнения, содержащие переменную под знаком корня называются иррациональными.) 2.Озвучьте определение корня уравнения. (Корень уравнения - это значение переменной , при подстановке которого в уравнение получаем верное равенство.) 3.Вспомните алгоритм и методы решения иррациональных уравнений:

g(x) ≥ 0

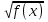=g (x)

f(x) = g² (x), (без проверки)

метод возведения обеих частей уравнения в одну и ту же степень;

сделав проверку, убеждаемся, являются ли они его корнями.

V. Историческая справка о происхождении арифметического корня.

Арифметический корень произошел от латинского слова radix - корень, radicalis - коренной. Начиная с 13 века,итальянские и другие европейские математики обозначали корень латинским словом radix ( сокращенно r). В 1525 г. в книге Х.Рудольфа "Быстрый и красивый счет при помощи искусных правил алгебры, обычно называемых Косс" появилось обозначение V - для квадратного корня, а V V V - обозначался кубический корень . В 1626 г. голландский математик А. Жирар ввел обозначения V, VV, VVV и т. д., которые вскоре вытеснил знак r, при этом над подкоренным выражением ставилась горизонтальная черта. Современное обозначение корня в виде впервые появилось в книге Рене Декарта "Геометрия", изданной в 1637 году.

VI. Математическая эстафета. Группа делится на две команды. Задания для эстафеты представлены на интерактивной доске.

Задание №1.

Составьте два иррациональных уравнения, из следующих составляющих:

для 1 команды- х,х², х^½,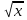 , ,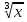36, 8, 93,+,=,+,-,-,=. . для 2 команды-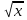 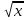, х^¾, х ,х³,3, 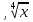,10, +,=,+,-,-,=. . Задание №2.

Какое из чисел является корнем уравнения:

для 1 команды- 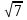= 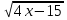, х=1, х = 0, х=6; для 2 команды- 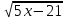= х-3 ,х=3, х=4, х=1. (Ответ: №1. Проверяем по определению, важно , чтобы переменная была под знаком корня или в дробной степени. №2. 1команда: Х=6-корень уравнения, 2 команда: х=1-корень уравнения).

VII. Решение иррациональных уравнений.

Задание. Решите иррациональные уравнения.

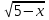1. = 4 - х 2) =

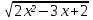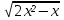
3) 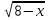= х - 1 4) 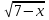= х

Четверо обучающихся решают иррациональные уравнения у доски , затем комментируют свои решения. Ответы заносят в таблицу . Если уравнения решены верно, то складывается зашифрованное слово «знания» (идет трансляция через вебкамеру). Это ключевое слово для перехода к следующему этапу урока, а остальные в это время решают уравнение из звуковой презентации.

VIII. Самостоятельная работа. Преподаватель: Итак, предыдущий этап показал , что вы готовы к самостоятельной работе с самопроверкой. Внимание на слайд. Проецируется проверочная работа на слайде, на два варианта.

№1.Какие из следующих уравнений являются иррациональными:

ӏ- вариант: а) х +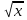 = 2; б) у² - 3у 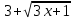= 4;

ӏӏ- вариант: а) х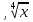 = 1+х; б) у + 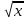+9 = 2.

№2. Является ли число корнем уравнения:

ӏ- вариант: х=4, ,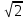

ӏӏ- вариант: х=2, .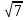

№3.Решите уравнение:

ӏ- вариант: 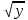= 2х + 1,

ӏӏ- вариант: х - 4 = .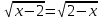

Ответы:

№1.Какие из следующих уравнений являются иррациональными:

ӏ- вариант: а). ӏӏ- вариант: б).

№2. Является ли число корнем уравнения:

ӏ- вариант:

х=4 - не является корнем уравнения, т.к. ,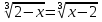

ӏӏ- вариант:

х=2-является корнем уравнения, т.к. , .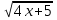

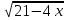
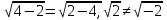№3.Решите уравнение:

ӏ- вариант: х₁= -1-посторонний корень, х₂=1. Ответ : 1.

ӏӏ- вариант: х₁= -1-посторонний корень, х=5. Ответ : 5.

Преподаватель: А теперь давайте оценим ваши знания. Поднимите руку у кого на счету за урок от 20 до 23 баллов ? вы , ребята , отлично потрудились на уроке и получаете отметку «5». Поднимите у кого на счету от 14 до 19 баллов? Я благодарю вас за хорошую работу на уроке, вы хорошо потрудились и получаете отметку «4». А кому же у нас не получилось набрать и 9 баллов ? Я сожалею , ребята , и прошу вас еще раз проработать материал дома , и тогда хорошие оценки непременно ждут вас на следующем уроке.

IX .Рефлексия. Обучающиеся оценивают успешность своей деятельности, отыскивают причины, приведшие к успеху и неудачам. На один и тот же вопрос отвечают несколько учащихся. Преподаватель наравне с учащимися высказывает своё мнение. Обучающиеся по очереди высказываются одним предложением, выбирая начало фразы из рефлексивного экрана:

1. Сегодня я узнал(а)…
2. Было интересно…
3. Было трудно…
4. Я выполнял(а) задания…
5. Я понял(а), что…
6. Теперь я могу…
7. Я почувствовал(а), что…
8. Я приобрел(а)…
9. Я научился(лась)…
10. У меня получилось …
11. Я смог(ла)…
12. Я попробую…
13. Меня удивило…
14. Урок дал мне для жизни…
15. Мне захотелось…

Преподаватель: Я думаю, для окончания нашего урока подходят

слова Ян Амос Коменского: "Учиться нелегко, но интересно".