- Учителю
- Урок по теме: ' Простейшие логарифмические неравенства' (10 класс)
Урок по теме: ' Простейшие логарифмические неравенства' (10 класс)
-
 Муниципальное бюджетное образовательное учреждение «Добровская школа-гимназия имени Я.М. Слонимского» Симферопольского района Республики Крым
Муниципальное бюджетное образовательное учреждение «Добровская школа-гимназия имени Я.М. Слонимского» Симферопольского района Республики Крым
-
Ступина Валентина Васильевна
-
Методическая разработка по теме
Простейшие логарифмические неравенства
по алгебре и началам математического анализа
для учащихся 10 классов
Симферополь, 2015 г.
Аннотация
Разработанные методические рекомендации включают 2 урока для 10 класса по алгебре и началам математического анализа по теме «Простейшие логарифмические неравенства». Данные рекомендации разработаны для использования школьными учителями на урока с использованием интерактивных технологий.
Данное методическое пособие разработано с учетом потребностей современного образовательного процесса на базе собственного многолетнего опыта преподавания с использованием интерактивных технологий с целью оптимизации учебно-воспитательного процесса.
Интерактивное обучение позволяет решать одновременно несколько задач, главной из которых является развитие коммуникативных умений и навыков, оно помогает установлению эмоциональных контактов между учащимися, обеспечивает воспитательную задачу, поскольку приучает работать в команде, прислушиваться к мнению своих товарищей, обеспечивает высокую мотивацию, прочность знаний, творчество и фантазию, коммуникабельность, активную жизненную позицию, ценность индивидуальности, свободу самовыражения, акцент на деятельность, взаимоуважение и демократичность. Использование интерактивных форм в процессе обучения, как показывает практика, снимает нервную нагрузку обучающихся (то есть присутствует элемент здоровьесбережения) дает возможность менять формы их деятельности, переключать внимание на узловые вопросы темы занятий.
Введение
Основная задача современной системы образования - обеспечить интеллектуальную грамотность и социальную адаптацию учащихся на основе приобретения ими положительного опыта в сфере обучения, познания, личностного развития и творчества.
Введение ФГОС определило требования к результатам обучения:
личностные, включающие готовность и способность обучающихся к саморазвитию, сформированность мотивации к обучению и познанию, ценностно-смысловые установки обучающихся, отражающие их индивидуально-личностные позиции, социальные компетенции, личностные качества; сформированность основ гражданской идентичности;
метапредметные, включающие освоение обучающимися универсальных учебных действий (познавательных, регулятивных и коммуникативных), обеспечивающих овладение ключевыми компетенциями, составляющими основу умения учиться, и межпредметными понятиями;
предметных, включающих освоенный обучающимися в ходе изучения учебного предмета опыт специфической для данной предметной области деятельности по получению нового знания, его преобразованию и применению, а также систему основополагающих элементов научного знания, лежащих в основе современной научной картины мира.
Методическая разработка соответствует следующим критериям: она актуальна, способна заинтересовать детей, соответствует рабочей учебной программе, учебнику, по которому изучается предмет, возрасту и психологическому состоянию детей, федеральным государственным образовательным стандартам и федеральным государственным образовательным требования.
Цель: создание методической разработки по алгебре и началам математического анализа для учащихся 10 классов по теме «Простейшие логарифмические неравенства».
Задачи:
-
Проанализировать различные источники знаний: учебники, рабочие учебные программы.
-
Связать данную тему с темой, изучаемой на предыдущем уроке («Простейшие показательные неравенства», учить находить аналогию в рассуждениях, научить делать выводы, аналогичные уже сделанным).
-
Подобрать практические задания к уроку по обеим темам.
-
Разработать систему контроля знаний.
Объектом исследования является преподавание темы «Простейшие логарифмические неравенства» в старшей школе.
Предмет исследования - оптимизация процесса обучения алгебре и началам математического анализа на школьных уроках с использованием интерактивных технологий.
Тема. Простейшие логарифмические неравенства (1-й урок по теме)
Цели:
1.Сформировать понятие логарифмического неравенства, сформулировать алгоритм решения простейшего логарифмического неравенства, первичные умения решения простейших логарифмических неравенств, представление о математике, как средстве моделирования явлений и процессов.
2.Развивать: абстрактное логическое мышление, математическую речевую грамотность, алгоритмическую культуру, навык к самостоятельной деятельности, навыки работы с различными источниками информации.
3. Воспитывать: культуру умственного труда: здоровье сберегающую компетентность, коммуникативные умения (умение работать в группе, умение сотрудничать), бережное отношение к школьному имуществу, в том числе к учебнику, воспитывать гражданина РК как субъекта РФ.
Оборудование: таблицы: «Свойства логарифмов», «Алгоритм решения простейшего логарифмического неравенства» (таблицы показывать в виде презентации, если позволяет оборудование кабинета).
Ход урока:
-
Организационный момент:
-
Повторение ранее изученного:
1.Проверка домашнего задания:
2.Математический мини-диктант:
Задание. Решить простейшие показательные неравенства.
Цель задания - проверка усвоения алгоритма решения простейшего показательного неравенства (сформированность предметной компетентности).
1 ученик («сильный») пишет на доске на развороте (с обратной стороны) и затем комментирует.
-
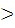 2)
2) 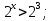 3)
3) 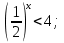 5;
5;
Проверка в парах с оцениванием.
Ответы: 1) х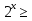 функция возрастающая на всей области определения (21), то по определению возрастающей функции: функцию f (х), определённую на некотором промежутке Х, называют возрастающей на этом промежутке, если для любой пары чисел
функция возрастающая на всей области определения (21), то по определению возрастающей функции: функцию f (х), определённую на некотором промежутке Х, называют возрастающей на этом промежутке, если для любой пары чисел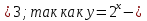 и
и 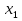
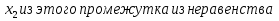 следует неравенство f
следует неравенство f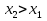 ;
;
-
х-2, так как функция
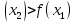 убывающая на всей области определения (0
убывающая на всей области определения (0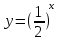 ) и, по определению убывающей функции: функцию f (х), определённую на некотором промежутке Х, называют убывающей на этом промежутке, если для любой пары чисел
) и, по определению убывающей функции: функцию f (х), определённую на некотором промежутке Х, называют убывающей на этом промежутке, если для любой пары чисел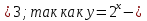 и
и 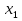 а
а 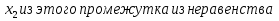 следует неравенство f
следует неравенство f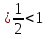 ;
;
3) 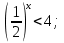 5,
5, 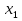 , х
, х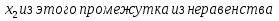 функция возрастающая на всей области определения (21), то по определению возрастающей функции: функцию f (х), определённую на некотором промежутке Х, называют возрастающей на этом промежутке, если для любой пары чисел
функция возрастающая на всей области определения (21), то по определению возрастающей функции: функцию f (х), определённую на некотором промежутке Х, называют возрастающей на этом промежутке, если для любой пары чисел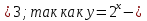 и
и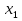
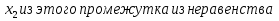
следует неравенство f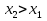 ;
;
III.Сообщение темы урока.
IV. Целеполагание (учащиеся формулируют чему они хотят научиться на этом уроке)
V.Мотивация учебной деятельности.
При изучении темы «Логарифмы» мы уже говорили о том для чего нужно изучать логарифмы: чтобы уметь строить и исследовать простейшие математические модели при решении прикладных задач, применять математические методы к исследованию процессов и явлений в природе. Примеры логарифмических спиралей: фотосъёмка из космоса природных явлений: штормы, ураганы, в астрономии - это галактики, в природе среди животных - раковины моллюсков, рост рогов у ряда животных и т.д.
VI. Актуализация опорных знаний.
Как уже было сказано ранее мы изучали функцию у =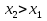 , где рассматривали два случая: 1) а
, где рассматривали два случая: 1) а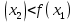 ; и 2) 0
; и 2) 0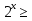
Делимся на 2 группы (правая и левая) и дальше работаем в группах, т.е. советуемся, помогаем друг другу, высказываем своё мнение, работаем со всеми возможными источниками информации (учебники, конспекты, справочный материал, интернет).
Задание: вспомнить свойства и вид графика функции у =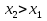
1 группа - при а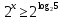 группа - при 0
группа - при 0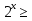
Время работы 2 минуты. Помним, что с учебником нужно обращаться аккуратно, т.к. по ним предстоит учиться младшим школьным товарищам ещё 5 лет, они присланы нам за счет бюджета РФ и являются собственностью школы.
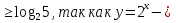 y
y
(a > 1)
0 1 x 0 1 x
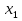
(0<a<1)
Спикеры от каждой группы выступают: дают характеристики функциям.
VII. Изучение нового материала.
Работа учащихся с учебником (с.178 , п.6.5) в группах по плану:
План:
1. Определение простейшего логарифмического неравенства.
2. Примеры простейших логарифмических неравенств.
I группа - 3. Решение логарифмических неравенств 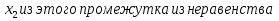 ,
,
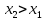 , при а
, при а 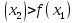 1.
1.
II группа 4. Решение логарифмических неравенств 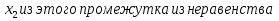 ,
,
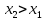 , при 0
, при 0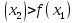 а
а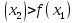 1.
1.
Выступают спикеры групп.
Таким образом, делаем вывод - алгоритм решения простейшего логарифмического неравенства:
Алгоритм:
1.Сравниваем значения логарифмических функций с равными основаниями.
2.Определяем свойство логарифмической функции (возрастающая или убывающая).
3.Применяем определение возрастающей/убывающей функции на промежутке, сравниваем аргументы.
4.Записываем ответ, не забывая учитывать область определения логарифмической функции.
Обратить внимание на ошибку, которую часто допускают учащиеся: не учитывают, что областью определения логарифмической функции является интервал (0;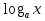 ).
).
VIII. Физкультурная минутка (Сан ПиН 2.4.2.2821-10).
Физкультминутка для улучшения мозгового кровообращения:
1.Исходное положение - сидя на стуле. 1 - 2 - отвести голову назад и плавно наклонить назад, 3 - 4 - голову наклонить вперёд, плечи не поднимать. Повторить 4-6 раз. Темп медленный.
2. Исходное положение сидя, руки на поясе. 1 - поворот головы направо, 2 - исходное положение, 3 - поворот головы налево, 4 - исходное положение. Повторить 6-8 раз. Темп медленный.
3.Исходное положение - стоя или сидя, руки на поясе. 1 - махом левую руку занести через правое плечо, голову повернуть налево, 2 - исходное положение, 3 - 4 - то же правой рукой. Повторить 4 - 6 раз. Темп медленный.
Физкультминутка для снятия утомления с плечевого пояса и рук.
1.Исходное положение стоя или сидя, руки на поясе. 1 - правую руку вперед, левую вверх. 2 - переменить положение рук. Повторить 3 - 3 раза, затем расслабленно опустить вниз потрясти кистями, голову наклонить вперёд. Темп средний.
2.Исходное положение - стоя или сидя, кисти тыльной стороны на поясе. 1 - 2 - свести локти вперёд, голову наклонить вперёд. 3 - 4 - локти назад, прогнуться. Повторить 6 -8 раз, затем руки вниз и потрясти расслабленно. Темп медленный.
3. Исходное положение - сидя, руки вверх. 1 - сжать кисти в кулак, 2 - разжать кисти. Повторить 6 - 8 раз, затем руки расслабленно опустить вниз и потрясти кистями. Темп средний.
IX. Первичное закрепление учебного материала:
1)Учитель показывает на доске, весь класс работает в тетрадях.
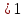 0
0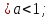 , (так как функция у=
, (так как функция у=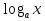 возрастающая, 5>1, областью определения логарифмической функции является интервал (0;
возрастающая, 5>1, областью определения логарифмической функции является интервал (0;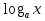 )).
)).
2)1 ученик работает у доски, все остальные ученики - в тетрадях.
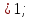 , (так как функция у =
, (так как функция у =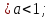 убывающая,
убывающая, 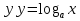 , областью определения логарифмической функции является интервал (0;
, областью определения логарифмической функции является интервал (0;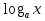 )).
)).
Ответ: 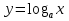
X. Формирование умений и навыков учащихся.
Работа в группах. Учебник с.177
I группа: №6.39(а), № 6.40(г), № 6.41 (а)
II группа: №6.39(б), №6.40 (в), №6.41(в)
Учащиеся из каждой группы выходят к доске, записывают и комментируют решения данных неравенств.
Ответы: №6.39(а) (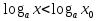 ), № 6.40(г) (0
), № 6.40(г) (0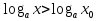 ), № 6.41 (а) (х
), № 6.41 (а) (х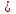 ).
).
№6.39(б) (х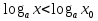 ), №6.40 (в) (х
), №6.40 (в) (х 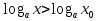 ), №6.41(в) (х
), №6.41(в) (х 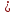 )
)
XI. Оценивание.
XII. Рефлексия: что мы узнали нового, чему научились, для чего это нужно знать человеку, в каких специальностях используются эти знания?
XIII. Домашнее задание (дифференцированное).
Основное:  читать, разобрать примеры из текста учебника, выучить алгоритм решения простейших логарифмических неравенств, №6.39(в,г), №6.40(д,е).
читать, разобрать примеры из текста учебника, выучить алгоритм решения простейших логарифмических неравенств, №6.39(в,г), №6.40(д,е).
Дополнительно (в соответствии с индивидуальной образовательной программой): №6.41(б,г),
Тема. Простейшие логарифмические неравенства (2-й урок по теме).
Цели:
1. Закрепить понятие логарифмического неравенства, формировать умения применения алгоритма решения простейшего логарифмического неравенства при решении неравенств.
2.Развивать: абстрактное логическое мышление, математическую речевую грамотность, алгоритмическую культуру, навык к самостоятельной деятельности, навыки работы с различными источниками информации.
3. Воспитывать: культуру умственного труда: здоровье сберегающую компетентность, коммуникативность (умение работать в группе, умение сотрудничать), бережное отношение к школьному имуществу, в том числе к учебнику, воспитывать гражданина РК как субъекта РФ.
Оборудование: таблицы: «Свойства логарифмов», «Алгоритм решения простейшего логарифмического неравенства» (таблицы показывать в виде презентации, если позволяет оборудование кабинета).
Ход урока:
-
Организационный момент:
-
Повторение ранее изученного:
1.Проверка домашнего задания:(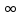 ) у доски 6 человек
) у доски 6 человек
№6.39(в) (Ответ: 0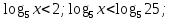 )- 1 ученик, №6.39(г) (Ответ: 0
)- 1 ученик, №6.39(г) (Ответ: 0 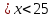 ) - 2 ученик, №6.40(д) (Ответ: 0
) - 2 ученик, №6.40(д) (Ответ: 0 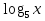 ) - 3 ученик, №6.40(е) (Ответ: х
) - 3 ученик, №6.40(е) (Ответ: х 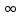 )- 4 ученик, №6.41(б) (Ответ: х
)- 4 ученик, №6.41(б) (Ответ: х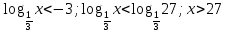 ) - 5 ученик, №6.41(г) (Ответ: 0
) - 5 ученик, №6.41(г) (Ответ: 0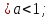 ) - 6 ученик.
) - 6 ученик.
2.Интерактивная игра: 3 команды (учащиеся, сидящие на 3-х рядах). Члены команд задают друг другу вопросы по теоретическому материалу, актуальному на данном уроке «Свойства логарифмов», алгоритм решения неравенства, определение возрастающей, убывающей функции.
3.Ответы учащихся у доски.
III.Сообщение темы.
IV.Целеполагание.
V.Мотивация учебной деятельности.
VI. Формирование умений и навыков:
1.Работа по учебнику:§6, п. 6.5., с 181 №6.41(а,в)
а) 5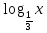 ОДЗ: х
ОДЗ: х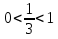
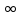
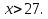
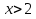
в) 3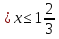 ОДЗ: х
ОДЗ: х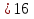
№6.42(а)
а) 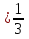 ОДЗ: х
ОДЗ: х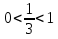
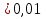
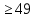
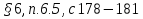
(1+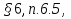 )
)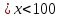 1,75
1,75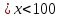
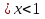
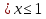 х
х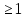 (областью определения функции у =
(областью определения функции у =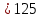 является интервал (0;
является интервал (0;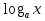 ), функция у =
), функция у =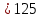 возрастающая,
возрастающая, 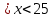 )
)
Ответ: х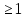
2.Физкультминутка
3.Самостоятельная работа (дифференцированно):
-Для учащихся базового уровня задания: №6.42 (б), 6.43(а)
№6.42(б)
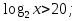 +
+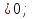 +
+ 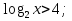
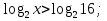
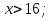 (1
(1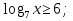 )
)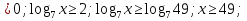
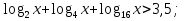 ;
;
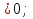
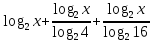 (областью определения функции у =
(областью определения функции у =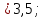 является интервал (0;
является интервал (0;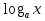 ), функция у =
), функция у =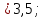 возрастающая,
возрастающая, 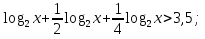 ).
).
Ответ: 0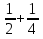
№6.43 (а)
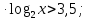 ;
;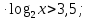
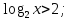 3
3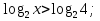
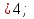
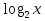
х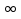 (областью определения функции у =
(областью определения функции у =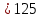 является интервал (0;
является интервал (0;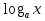 ), функция у =
), функция у =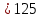 возрастающая,
возрастающая, 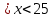 ).
).
Ответ: х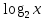
-Для учащихся, с более высокой подготовкой (профильный уровень):№6.44(а,б)
а) 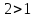
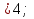
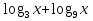
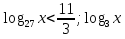 0
0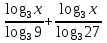 (областью определения функции у =
(областью определения функции у =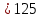 является интервал (0;
является интервал (0;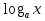 ), функция у =
), функция у =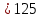 возрастающая,
возрастающая, 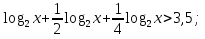 ).
).
Ответ: 0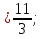
б) 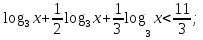 ;
; 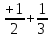
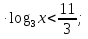
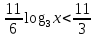 х
х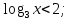 (областью определения функции у =
(областью определения функции у =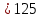 является интервал (0;
является интервал (0;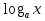 ), функция у =
), функция у =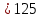 возрастающая,
возрастающая, 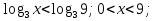 ).
).
Ответ: х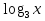
Тетради сдать на проверку.
VII.Рефлексия: что мы узнали нового, чему научились?
VIII.Домашнее задание (дифференцированное).
Основное: 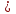 читать, повторять свойства логарифмов, алгоритм решения простейших логарифмических неравенств, №6.43 (б,в)
читать, повторять свойства логарифмов, алгоритм решения простейших логарифмических неравенств, №6.43 (б,в)
Дополнительно (в соответствии с индивидуальной образовательной программой): №6.44(в).