Урок по математике на тему 'Путешествие по стране логарифмов' (11 класс)

Урок по алгебре и началам анализа в 11 классе.

Тема урока: «Путешествие по стране логарифмов».

Форма проведения: урок обобщения и систематизации знаний.

Цели урока:

• Обобщение, закрепление и контроль знаний по теме «Логарифм и его свойства, логарифмические уравнения и неравенства».

• Воспитание внимательности, активности, ответственности, толерантности.

• Развитие навыка самооценки работы на уроке.

Оборудование: доска, отпечатанный раздаточный материал.

Эпиграф: «Учиться можно только весело... Чтобы переварить знания, надо поглощать их с аппетитом».

Анатоль Франс.

Класс разбивается на команды по 5 человек. Каждая команда выбирает капитана.

I этап. Разминка.

На этом этапе идёт проверка знания теории. Капитан каждой команды выбирает по 4 карточки с вопросами по теории. Команда совещается 1 минуту, а затем даёт ответы на вопросы. Участник команды, правильно ответивший на вопрос, получает зачётный балл. Если команда затрудняется ответить, то это может сделать любой ученик из другой команды и получить зачётный балл. (Приложение 1)

II этап. Примени свойства логарифмов.

Каждый ученик получает карточку с заданиями по свойствам логарифмов. Задания на карточке разноуровневые. Выполнение задач проверяется учителем после урока. (Приложение 2)

III этап. В мире логарифмических уравнений.

Каждый учащийся получает карточку с заданием. Наиболее подготовленным ученикам предлагаются более сложные задания, которые они решают у доски. Работы проверяются учителем после урока. (Приложение 3)

IV этап. Устный счёт: отдых для ума.

(Приложение 4)

V этап. Логарифмические неравенства на ЕГЭ.

Учащиеся выполняют задания по карточкам. Наиболее подготовленные работают у доски. Работы проверяются учителем после урока. (Приложение 5)

Подведение итогов проводится в конце урока.

Приложение 1.

1. Дайте определение логарифма числа.

2. Запишите основное логарифмическое тождество.

3. Запишите формулу логарифм произведения.

4. Запишите формулу логарифм частного.

5. Запишите формулу логарифм степени.

6. Запишите формулу логарифмического перехода от одного основания к другому.

7. Когда логарифм равен 1, 0?

8. Какие логарифмы называются десятичными, натуральными и как они обозначаются?

9. Дайте определение логарифмической функции.

10. Какие область определения и область значений логарифмической функции?

11. В каком случае функция y=log_ax является убывающей, в каком - возрастающей?

12. При каких значениях х функция y=log_ax принимает положительные значения, при каких отрицательные?

Приложение 2.

К-1

Вычислите:

3. Во сколько раз объём куба с ребром больше объёма куба с ребром ?

К-2

Вычислите:

3. Найдите площадь круга, если длина его радиуса равна значению выражения

К-3

Вычислите:

1. 

2. .

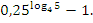
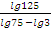3.Найдите длину окружности, если длина радиуса численно равна значению выражения :.

К-4

Вычислите:

1. 

2. .

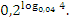
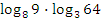3.Найдите объём куба, если длина его ребра численно равна значению выражения: ).

К-5

Вычислите:

3.Найдите площадь квадрата, если длина его стороны численно равна значению выражения:

Ответы на задания II этапа

№карточки

№задания

1

2

3

4

5

1

6

-3

-0,8

2

2

2

6

125

1,5

4

0,5

3

1

16

Приложение 3.

К-1

Решите уравнения:

1. log₃(x - 2) = 2;

2. log₃(2x - 4) =l og₃(x + 7);

3. 3log₈²x + 5log₈x = 2;

4. x^lgx = 10000x².

К-2

Решите уравнения:

1. log₂(x - 3) = 2;

2. log₄(2x - 1) = log₄(3x - 3);

3. 2log₉²x = 2 - 3log₉x;

4. x^{lgx - 2} = 1000.

К-3

Решите уравнения:

1. log₅(x + 6) = 1;

2. log₇(4x + 3) = log₇(x + 6);

3. 3lg²x - 10lgx + 3 = 0;

4. (x + 7)^{lg(x + 7)} = 10.

К-4

Решите уравнения:

1. log₁₃(x - 4) = 1;

2. log₅(2x + 3) = log₅(x + 5);

3. 2log₄²x + 5log₄x - 3 = 0;

4. x^log₃^{x - 4} = .

К-5

Решите уравнения:

1. log₂(x + 1) = 3;

2. log₂(3x + 4) = log₂(x + 6);

3. 3log_1\8²x + 5log_1\8x - 2 = 0;

4. x^log₂^{x +2} = 256.

К-1

Решите уравнение:

.

К-2

Решите уравнение:

.

К-3

Решите уравнение:

.

К-4

Решите уравнение:

.

К-5

Решите уравнение:

.

К-6

Решите уравнение:

.

Приложение 4.

Даны выражения:

1. 

2. 

3. 

4. 

5. 

6. 

7. 

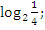
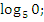
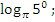
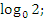
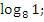
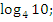
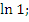
8. lg10;

9. 

10. 

11. 

12. 

13. 

14. 

15. .

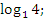
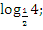
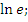
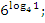
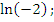
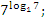
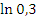Выберите те, которые:

1. не имеют смысла;

2. равны 0;

3. равны 1;

4. отрицательные;

5. не являются целыми.

Приложение 5.

К - 1

1. Решите неравенство:

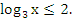
2. Найдите область определения функции: .

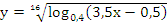3. Найдите число целых решений неравенства:.

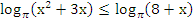К - 2

1. Решите неравенство:

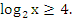
2. Найдите область определения функции :.

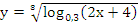3. Найдите число целых решений неравенства:.

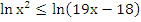К- 3

1. Решите неравенство:

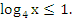
2. Найдите область определения функции: .

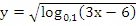3. Найдите число натуральных решений неравенства:.

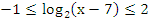К- 4

1. Решите неравенство:

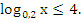
2. Найдите область определения функции: .

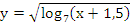3. Сколько натуральных решений имеет неравенства:?

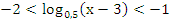К - 5

1. Решите неравенство: .

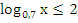2. Найдите область определения функции: .

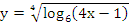3. Сколько натуральных чисел являются решениями неравенства: ?

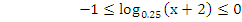К - 6

Найдите все значения х, для которых точки графика функции лежат выше соответствующих точек графика функции .

К - 7

Найдите все значения х, для которых точки графика функции лежат ниже соответствующих точек графика функции .

К - 8

Найдите все значения х, для которых точки графика функции лежат не выше соответствующих точек графика функции .