Календарно - тематическое планирование уроков на 2014-2015 уч. год

Алгебра -7

Учитель Обласова Юлия Абдуварисовна

Классы : 7 А

Программы: Алгебра 7-9 классы авт-сост. И.И. Зубарева, А.Г. Мордкович - М.: Мнемозина, 2010.- 63с.

Учебные материалы:

а) учебник Мордкович А.Г. «Алгебра часть 1. Учебник», «Алгебра часть 2. Задачник»- М.: Мнемозина, 2011

б) Дидактические материалы:

1. Алгебра и геометрия, самостоятельные и контрольные работы, А.П. Ершова, Москва, Илекса, 2009г.

2. Алгебра, тренажер. Тематические тесты и итоговые работы 7-8 класс, под ред. Ф.Ф.Лысенко,Ростов - на - Дону, Легион, 2013

3. М.А. Попов «Контрольные и самостоятельные работы по алгебре к учебнику А.Г. Мордковича. 7 класс». Москва «Экзамен » 2014.

4. Методическое обеспечение: А.Н. Рурукин «Поурочные разработки по алгебре к УМК А.Г.Мордковича» Москва. ВАКО.2010г,

Количество часов по программе : 105 (3 ч. в неделю)

Форма контроля: контрольные работы: 8. Добавлена контрольная работа по теме у = х².

Пояснительная записка

Статус документа

Настоящая программа по математике для основной общеобразовательной школы 7 класса составлена на основе федерального компонента государственного стандарта основного общего образования (приказ МОиН РФ от 05.03.2004г. № 1089), примерных программ по алгебре и геометрии (письмо Департамента государственной политики в образовании Минобрнауки России от 07.07.2005г. № 03-1263), «Временных требований к минимуму содержания основного общего образования» (приказ МО РФ от 19.05.98. № 1236), сборник "Программы для общеобразовательных школ" . Алгебра 7 кл. / Сост. Мордкович, Геометрия 7-9кл./Сост.Атанасян

Примерная программа конкретизирует содержание предметных тем образовательного стандарта и даёт примерное распределение учебных часов по разделам курса.

Цели изучения:

• овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования;

• интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе: ясность и точность мысли, критичность мышления, интуиция, логическое мышление, элементы алгоритмической культуры, пространственных представлений, способность к преодолению трудностей;

• формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;

• воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, понимание значимости математики для научно-технического прогресса.

• систематическое развитие понятия числа;

• выработка умений выполнять устно и письменно арифметические действия над числами, переводить практические задачи на язык математики;

Общая характеристика учебного предмета

Математическое образование в основной школе складывается из следующих содержательных компонентов (точные названия блоков): арифметика; алгебра; геометрия; элементы комбинаторики, теории вероятностей, статистики и логики. В своей совокупности они отражают богатый опыт обучения математике в нашей стране, учитывают современные тенденции отечественной и зарубежной школы и позволяют реализовать поставленные перед школьным образованием цели на информационно емком и практически значимом материале. Эти содержательные компоненты, развиваясь на протяжении всех лет обучения, естественным образом переплетаются и взаимодействуют в учебных курсах.

Арифметика призвана способствовать приобретению практических навыков, необходимых для повседневной жизни. Она служит базой для всего дальнейшего изучения математики, способствует логическому развитию и формированию умения пользоваться алгоритмами.

Алгебра Изучение алгебры нацелено на формирование математического аппарата для решения задач из математики, смежных предметов, окружающей реальности. Язык алгебры подчеркивает значение математики как языка для построения математических моделей, процессов и явлений реального мира (одной из основных задач изучения алгебры является развитие алгоритмического мышления, необходимого, в частности, для освоения курса информатики; овладение навыками дедуктивных рассуждений. Преобразование символических форм вносит свой специфический вклад в развитие воображения, способностей к математическому творчеству. Другой важной задачей изучения алгебры является получение школьниками конкретных знаний о функциях как важнейшей математической модели для описания и исследования разнообразных процессов (равномерных, равноускоренных, экспоненциальных, периодических и др.), для формирования у обучающихся представлений о роли математики в развитии цивилизации и культуры.

Геометрия - один из важнейших компонентов математического образования, необходимый для приобретения конкретных знаний о пространстве и практически значимых умений, формирования языка описания объектов окружающего мира, для развития пространственного воображения и интуиции, математической культуры, для эстетического воспитания обучающихся. Изучение геометрии вносит вклад в развитие логического мышления, в формирование понятия доказательства.

Элементы логики, комбинаторики, статистики и теории вероятностей становятся обязательным компонентом школьного образования, усиливающим его прикладное и практическое значение. Этот материал необходим, прежде всего, для формирования функциональной грамотности - умений воспринимать и анализировать информацию, представленную в различных формах, понимать вероятностный характер многих реальных зависимостей, производить простейшие вероятностные расчёты. Изучение основ комбинаторики позволит учащемуся осуществлять рассмотрение случаев, перебор и подсчёт числа вариантов, в том числе в простейших прикладных задачах.

При изучении статистики и теории вероятностей обогащаются представления о современной картине мира и методах его исследования, формируется понимание роли статистики как источника социально значимой информации и закладываются основы вероятностного мышления.

Таким образом, в ходе освоения содержания курса учащиеся получают возможность:

• развить представление о числе и роли вычислений в человеческой практике; сформировать практические навыки выполнения устных, письменных, инструментальных вычислений, развить вычислительную культуру;

• овладеть символическим языком алгебры, выработать формально-оперативные алгебраические умения и научиться применять их к решению математических и нематематических задач;

• изучить свойства и графики элементарных функций, научиться использовать функционально-графические представления для описания и анализа реальных зависимостей;

• развить пространственные представления и изобразительные умения, освоить основные факты и методы планиметрии, познакомиться с простейшими пространственными телами и их свойствами;

• получить представления о статистических закономерностях в реальном мире и о различных способах их изучения, об особенностях выводов и прогнозов, носящих вероятностный характер;

• развить логическое мышление и речь - умения логически обосновывать суждения, проводить несложные систематизации, приводить примеры и контрпримеры, использовать различные языки математики (словесный, символический, графический) для иллюстрации, интерпретации, аргументации и доказательства;

• сформировать представления об изучаемых понятиях и методах как важнейших средствах математического моделирования реальных процессов и явлений.

Курс алгебры построен в соответствии с традиционными содержательно-методическими линиями: числовой, функциональной, алгоритмической, уравнений и неравенств, алгебраических преобразований. В курсе алгебры 7-го класса продолжается систематизация сведений о преобразовании выражений и решении уравнений с одним неизвестным. Специальное внимание уделяется новым вопросам: употреблению знаков 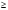или 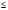, записи и чтению двойных неравенств, понятиям тождества, тождественного преобразования, линейного уравнения с одним неизвестным, равносильных уравнений. Формируется понятие функции, что является начальным этапом в обеспечении систематической функциональной подготовки учащихся. Продолжается изучение степени с натуральным показателем. Изучаются свойства функци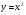й и 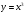, и особенности расположения их графиков в координатной плоскости. Главное место занимают алгоритмы действий с многочленами - сложение, вычитание и умножение. Особое внимание уделяется разложению многочленов на множители с помощью вынесения за скобки общего множителя и с помощью группировки. Вырабатываются умения применять формулы сокращенного умножения как для преобразования произведения в многочлен, так и для разложения на множители. Даются первые знания по решению систем линейных уравнений с двумя переменными, что позволяет значительно расширить круг текстовых задач. Серьезное внимание уделяется формированию умений рассуждать, делать простые доказательства, давать обоснования выполняемых действий.

Программой отводится на изучение алгебры 3 часа в неделю, что составляет 105 часов в учебный год.

Данное планирование определяет достаточный объем учебного времени для повышения математических знаний учащихся в среднем звене школы, улучшения усвоения других учебных предметов.

Промежуточная аттестация проводится в форме тестов, самостоятельных, проверочных работ и математических диктантов (по 10 - 15 минут) в конце логически законченных блоков учебного материала.

В курсе геометрии 7-го класса расширяются сведения о геометрических фигурах. На начальном этапе основное внимание уделяется двум аспектам: понятию равенства геометрических фигур (отрезков и углов) и свойствами измерения отрезков и углов. Главное место занимают признаки равенства треугольников. Формируются умения выделять равенство трех соответствующих элементов данных треугольников и делать ссылки на изученные признаки. Особое внимание уделяется доказательству параллельности прямых с использованием соответствующих признаков. Теорема о сумме углов треугольника позволяет получить важные следствия, что существенно расширяет класс решаемых задач. Серьезное внимание уделяется формированию умений рассуждать, делать простые доказательства, давать обоснования выполняемых действий.

Программой отводится на изучение геометрии по 2 урока в неделю, что составляет 70 часа в учебный год.

Данное планирование определяет достаточный объем учебного времени для повышения геометрических знаний учащихся в среднем звене школы, улучшения усвоения других учебных предметов.

Промежуточная аттестация проводится в форме тестов, самостоятельных, проверочных работ и математических диктантов (по 10 - 15 минут) в конце логически законченных блоков учебного материала.

Требования к уровню подготовки учащихся.

В результате изучения курса алгебры 7-го класса учащиеся должны уметь:

• бегло и уверенно выполнять арифметические действия с рациональными числами; осуществлять в выражениях и формулах числовые подстановки и выполнять соответствующие вычисления;

• выполнять тождественные преобразования выражений: приведение подобных слагаемых, раскрытие скобок со знаком «плюс» или «минус» пред скобками;

• решать уравнения с одним неизвестным и применять уравнения к решению текстовых задач; решать системы линейных уравнений;

• строить графики функций 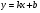, (b≠0), 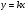; понимать как влияет знак коэффициента k на расположение в координатной плоскости графика функции 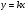, где k≠0, как зависит от значений k и b взаимное расположение графиков двух функций вида 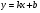; видеть эту зависимость.

• выполнять основные действия со степенями с натуральным показателем, с многочленами; выполнять разложение многочленов на множители;

• понимать графическую интерпретацию решения уравнений и систем уравнений;

• понимать содержательный смысл важнейших свойств функции; по графику функции отвечать на вопросы, касающиеся её свойств; строить графики функций - линейной, квадратичной функции и функции ;

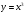• использовать приобретенные знания, умения, навыки в практической деятельности и повседневной жизни для:

  • решения несложных практических расчетных задач, в том числе с использованием при необходимости справочной литературы, калькулятора, компьютера;

  • устной прикидки, и оценки результата вычислений, проверки результата вычислений выполнением обратных действий;

  • моделирования практических ситуаций и исследовании построенных моделей с использованием аппарата алгебры;

  • интерпретации графиков реальных зависимостей между величинами.

В результате изучения курса геометрии 7-го класса учащиеся должны уметь:

• пользоваться геометрическим языком для описания предметов окружающего мира;

• распознавать на чертежах и моделях геометрические фигуры (отрезки, углы, треугольники и их частные виды), различать их взаимное расположение;

• изображать геометрические фигуры; выполнять чертежи по условию задач; осуществлять преобразование фигур;

• вычислять значения геометрических величин (длин отрезков, градусную меру углов);

• решать геометрические задания, опираясь на изученные свойства фигур и отношений между ними, применяя дополнительные построения, алгебраический аппарат;

• проводить доказательные рассуждения при решении задач, используя известные теоремы, обнаруживая возможности для их использования;

• решать простейшие планиметрические задачи в пространстве.

• использовать приобретенные знания, умения, навыки в практической деятельности и повседневной жизни для:

  • описания реальных ситуаций на языке геометрии;

  • решения практических задач;

  • построений геометрическими инструментами (линейка, угольник, циркуль, транспортир).

Учебно-тематический план

Алгебра

№п/п

Название раздела

Количество часов

Теория

Контрольные работы

Всего

повторение

3

1

4

Математический язык. Математическая модель.

11

1

12

Линейная функция

10

1

11

Системы двух линейных уравнений с двумя переменными

12

1

13

Степень с натуральным показателем и ее свойства

6

6

Одночлены. Арифметические операции над одночленами

7

1

8

Многочлены. Арифметические операции над многочленами

14

1

15

Разложение многочлена на множители

17

1

18

Функция .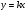

8

1

9

Итоговое повторение

10

1

10

Всего:

96

9

105

Геометрия

№п/п

Название раздела

Количество часов

Теория

Контрольные работы

Всего

Начальные геометрические сведения

9

1

10

Треугольники

16

1

17

Параллельные прямые

12

1

13

Соотношение между сторонами и углами треугольника

17

2

19

Итоговое повторение

9

-

9

Итоговая контрольная работа

1

1

2

Всего:

64

6

70

Критерии и нормы оценки знаний, умений и навыков обучающихся по математике.

1. Оценка письменных контрольных работ обучающихся по математике.

Ответ оценивается отметкой «5», если:

• работа выполнена полностью;

• в логических рассуждениях и обосновании решения нет пробелов и ошибок;

• в решении нет математических ошибок (возможна одна неточность, описка, которая не является следствием незнания или непонимания учебного материала).

Отметка «4» ставится в следующих случаях:

• работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);

• допущены одна ошибка или есть два - три недочёта в выкладках, рисунках, чертежах или графиках (если эти виды работ не являлись специальным объектом проверки).

Отметка «3» ставится, если:

• допущено более одной ошибки или более двух - трех недочетов в выкладках, чертежах или графиках, но обучающийся обладает обязательными умениями по проверяемой теме.

Отметка «2» ставится, если:

• допущены существенные ошибки, показавшие, что обучающийся не обладает обязательными умениями по данной теме в полной мере.

Учитель может повысить отметку за оригинальный ответ на вопрос или оригинальное решение задачи, которые свидетельствуют о высоком математическом развитии обучающегося; за решение более сложной задачи или ответ на более сложный вопрос, предложенные обучающемуся дополнительно после выполнения им каких-либо других заданий.

2. Оценка устных ответов обучающихся по математике

Ответ оценивается отметкой «5», если ученик:

• полно раскрыл содержание материала в объеме, предусмотренном программой и учебником;

• изложил материал грамотным языком, точно используя математическую терминологию и символику, в определенной логической последовательности;

• правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;

• показал умение иллюстрировать теорию конкретными примерами, применять ее в новой ситуации при выполнении практического задания;

• продемонстрировал знание теории ранее изученных сопутствующих тем, сформированность и устойчивость используемых при ответе умений и навыков;

• отвечал самостоятельно, без наводящих вопросов учителя;

• возможны одна - две неточности при освещении второстепенных вопросов или в выкладках, которые ученик легко исправил после замечания учителя.

Ответ оценивается отметкой «4», если удовлетворяет в основном требованиям на оценку «5», но при этом имеет один из недостатков:

• в изложении допущены небольшие пробелы, не исказившее математическое содержание ответа;

• допущены один - два недочета при освещении основного содержания ответа, исправленные после замечания учителя;

• допущены ошибка или более двух недочетов при освещении второстепенных вопросов или в выкладках, легко исправленные после замечания учителя.

Отметка «3» ставится в следующих случаях:

• неполно раскрыто содержание материала (содержание изложено фрагментарно, не всегда последовательно), но показано общее понимание вопроса и продемонстрированы умения, достаточные для усвоения программного материала (определены «Требованиями к математической подготовке обучающихся» в настоящей программе по математике);

• имелись затруднения или допущены ошибки в определении математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов учителя;

• ученик не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме;

• при достаточном знании теоретического материала выявлена недостаточная сформированность основных умений и навыков.

Отметка «2» ставится в следующих случаях:

• не раскрыто основное содержание учебного материала;

• обнаружено незнание учеником большей или наиболее важной части учебного материала;

• допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов учителя.

Общая классификация ошибок.

При оценке знаний, умений и навыков обучающихся следует учитывать все ошибки (грубые и негрубые) и недочёты.

Грубыми считаются ошибки:

• • незнание определения основных понятий, законов, правил, основных положений теории, незнание формул, общепринятых символов обозначений величин, единиц их измерения;

  • незнание наименований единиц измерения;

  • неумение выделить в ответе главное;

  • неумение применять знания, алгоритмы для решения задач;

  • неумение делать выводы и обобщения;

  • неумение читать и строить графики;

  • неумение пользоваться первоисточниками, учебником и справочниками;

  • потеря корня или сохранение постороннего корня;

  • отбрасывание без объяснений одного из них;

  • равнозначные им ошибки;

  • вычислительные ошибки, если они не являются опиской;

  • логические ошибки.

К негрубым ошибкам следует отнести:

• • неточность формулировок, определений, понятий, теорий, вызванная неполнотой охвата основных признаков определяемого понятия или заменой одного - двух из этих признаков второстепенными;

  • неточность графика;

  • нерациональный метод решения задачи или недостаточно продуманный план ответа (нарушение логики, подмена отдельных основных вопросов второстепенными);

  • нерациональные методы работы со справочной и другой литературой;

  • неумение решать задачи, выполнять задания в общем виде.

Недочетами являются:

• • нерациональные приемы вычислений и преобразований;

  • небрежное выполнение записей, чертежей, схем, графиков.

УМК включает в себя:

1. Мордкович А.Г., Алгебра, 7 класс. Учебник, задачник для учащихся общеобразовательных учреждений. М.; Мнемозина. 2011.

2. Программы. Математика. 5-6 классы. Алгебра. 7-9 классы. Алгебра и начала математического анализа. 10-11 классы. Авт.-сост.: И.И. Зубарева, А.Г. Мордкович

3. Александрова Л.А., Алгебра-7. Контрольные работы./Под ред. Мордковича А.Г. М.; Мнемозина. 2009.

4. Александрова Л.А., Алгебра-7.Самостоятельные работы./Под ред. Мордковича А.Г. М.; Мнемозина. 2009.

5. Мордкович А. Г. Алгебра. 7 класс : методическое пособие для учителя / А. Г. Мордкович. - М.: Мнемозина, 2008

6. Мордкович А.Г. Алгебра. 7-9 классы. Тесты для учащихся общеобразовательных учреждений / А. Г. Мордкович, Е. Е. Тульчинская. - 7-е изд., перераб. - М.: Мнемозина, 2008.

7. Тульчинская Б. Е. Алгебра. 7 класс. Блицпрос : пособие для учащихся общеобразоват. учреждений / Е. Е. Тульчинская. - 4-е изд., испр. и доп. - М. : Мнемозина, 2008.

8. Попов, М.А. Контрольные и самостоятельные работы по алгебре: 7 класс: к учебнику А.Г Мордковича «Алгебра. 7 класс» / М.А. Попов. - 4-е изд., перераб и доп. - М.: Издательство «Экзамен», 2010.

1. Геометрия, 7 - 9: Учеб. для общеобразоват. учреждений/ Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. - М.: Просвещение, 2014.

2. Программы для общеобразовательных учреждений Геометрия 7-9 Автор состав. Т.А.Бурмистрова - М.: Просвещение, 2008.

3. Л. С. Атанасян, В. Ф. Бутузов, Ю. А. Глазков, И. И. Юдина Геометрия: Рабочая тетрадь. 7 класс: пособие для учащихся общеобразовательных учреждений. - 13-е изд. - - М.: Просвещение, 2010.

4. Зив Б. Г. Геометрия. Дидактические материалы. 7 класс / Б. Г. Зив, В. М. Мейлер. - 16-е изд. - М. : Просвещение, 2010.

5. Изучение геометрии в 7-9 классах. Пособие для учителей/Атанасян Л.С., Бутузов В.Ф., Глазков Ю.А. и др.. - 7-е изд. -М., Просвещение, 2009,

6. Мельникова, Н.Б. Контрольные работы по геометрии: 7 класс: к учебнику Л.С. Атанасяна, В.Ф. Бутуэова, СБ. Кадомцева и др. «Геометрия. 7-9» / Н.Б. Мельникова. - М.: Издательство «Экзамен», 2009.

7. Фарков, А.В. Тесты по геометрии: 7 класс: к учебнику Л.С, Атанасяна и др. «Геометрия. 7-9» / А.В. Фарков. - М.: Издательство «Экзамен», 2009.

Интернет-ресурсы:

Вся элементарная математика: Средняя математическая интернет-школа

http://www.bymath.net

Графики функций

http://graphfunk.narod.ru

Задачник для подготовки к олимпиадам по математике

http://tasks.ceemat.ru

Занимательная математика - школьникам (олимпиады, игры, конкурсы по математике)

http://www.math-on-line.com

Интернет-проект «Задачи»

http://www.problems.ru

Математические этюды

http://www.etudes.ru

Математические олимпиады и олимпиадные задачи

http://www.zaba.ru

Международный математический конкурс «Кенгуру»

http://www.kenguru.sp.ru

Методика преподавания математики

http://methmath.chat.ru

Московская математическая олимпиада школьников

Газета «Математика» Издательского дома «Первое сентября»

http://mat.1september.ru

Математика в Открытом колледже

http://www.mathematics.ru

Math.ru: Математика и образование

http://www.math.ru

Московский центр непрерывного математического образования (МЦНМО)

http://www.mccme.ru

Allmath.ru - вся математика в одном месте

http://www.allmath.ru

Тема, кол-во часов

Дата

Тип урока

Планируемые результаты

Форма орг. деят.

Формы контроля

Оборудование

Примечание

планируемая

фактическая

Знать/ понимать

Уметь/ применять

Повторение курса

6 класса

1

Совместные действия над обыкновенными и десятичными дробями.

1.9

Закрепление практических умений

Действия над обыкновенными и десятичными дробями

фронтальная

Устный опрос по теории

Задания для индивидуальной работы

2

Отношения. Пропорции.

3.9

Закрепление практических умений

Понятия: отношения, пропорции

фронтальная

Задания для индивидуальной работы

3

Решение задач с помощью уравнений.

4.9

Закрепление практических умений

Умение решению задач с помощью уравнений.

фронтальная

Задания для индивидуальной работы

4

Самостоятельная работа по теме: «Входящий контроль»

8.9

Контроль полученных ЗУН

-обобщать и систематизировать знания по основным темам курса математики 6 класса;

-предвидеть возможные последствия своих действий

индивидуальная

тестирование

Глава 1

Математический язык. Математическая модель 12 часов

5

Числовые и алгебраические выражения

10.9

Изучение нового материала

понятия: числовое выражение, алгебраическое выражение, значение выражения, переменная, допустимое и недопустимое значение переменной.

излагать информацию, интерпретируя факты, разъясняя значение и смысл теории

групповая

презентация

6

Числовые и алгебраические выражения

11.9

Изучение нового материала

Понятие алгебраического выражения

находить значение алгебраическо-

го выражения при заданных значениях переменных; - воспринимать устную речь, проводить информационно-смысловой анализ текста и лекции, приводить и разбирать примеры

при которых имеет смысл выражение; - участвовать в диалоге, отражать в письменной форме свои решения, работать с математическим справочником, выполнять и оформлять тестовые задания

индивидуальная

фронтальная

7

Числовые и алгебраические выражения

15.9

Закрепление полученных знаний

Значение числового выражения и их доп. значений

индивидуальная

фронтальная

Устный опрос по теории, с/р

8

Что такое математический язык

17.9

Изучение нового материала

Математическое буквенное выражение, математические утверждения, математический язык

- осуществлять «перевод» выражений с математического языка на обычный язык и обратно; давать оценку информации, фактам, процессам, определять их актуальность

групповая

презентация

9

Что такое математический язык.

18.9

Закрепление

изученного

материала

понятие математической

модели.

составлять математическую модель реальной ситуации, используя математический язык;

- искать несколько способов решения -аргументировать рациональный способ, проводить доказательные рассуждения

практическая работа

Самостоятельная работа

Задания для индивидуальной работы

10

Что такое математическая модель

22.9

Изучение нового материала

Понятие «математическое моделирование»

- решать текстовые

задачи, выделяя три этапа математического моделирования; адекватно воспринимать устную речь, проводить информационно-смысловой анализ текста, приводить прим.

индивидуальная

фронтальная

Устный опрос по теории

презентация

11

Что такое математическая модель

24.9

Закрепление нов. материала + контроль ЗУН

Составление графической модели

семинар

Проверочная работа

Индивидуальные карточки

12

Линейное уравнение с одной переменной

25.9

Изучение нового материала

Систематизация обобщение сведений о решении уравнений с одним неизвестным, Формировать умения решать уравнения с одним неизвестным и применять уравнения к решению задач;

Уметь решать линейные уравнения с одной переменной.

лекция

индивидуальная

фронтальная

презентация

13

Линейное уравнение с одной переменной

29.9

Закрепление

изученного

материала

Линейное уравнение с одной переменной, переменная, корни уравнения.

Уметь решать линейные уравнения с одной переменной.

индивидуальная

фронтальная

Тест

Презентация

14

Координатная прямая

1.10

Изучение нового материала

Понятие геометрическая модель. Термины: числовые промежутки, луч, открытый луч, интервал, отрезок, полуинтервал

Уметь связывать геометрическую и аналитическую модели числового промежутка, выбирать обозначение и символическую запись

индивидуальная

семинар

15

Координатная прямая.

2.10

Закрепление

изученного

материала

Координатная прямая, координата точки, числовой промежуток, интервал, полуинтервал, отрезок, открытый луч, луч

практическая работа

Устный опрос по теории Самостоятельная работа

Презентация

16

Контрольная работа №1

6.10

Контроль ЗУН

Уметь обобщать и систематизировать знания по теме

индивидуальная

Контрольная работа

Задания для индивидуальной работы

II.

Линейная функция 11 часов

Задания для индивидуальной работы

18

Координатная плоскость

8.10

Изучение нового материала +

Практическое

занятие

Понятия: прямоугольная система координат, абсцисса и ордината точки, ось абсцисс, ось ординат

Строить на координатной плоскости точки и фигуры по заданным координатам; определять координаты точек. Определять, является ли пара чисел решением данного уравнения с двумя переменными; приводить примеры решений уравнений с двумя переменными;

индивидуальная

фронтальная

19

Координатная плоскость

9.10

Применение ЗУН

групповая

Самостоятельная работа

Презентация

20

Линейное уравнение с двумя переменными

13.10

Изучение нового материала.

Понятия линейного уравнения с двумя переменными, его решения.

решать задачи, алгебраической моделью которых является уравнение с двумя переменными; находить целые решения путем перебора.

Строить графики линейных уравнений с двумя переменными.

индивидуальная

фронтальная

Устный опрос по теории

21

Линейное уравнение с двумя переменными и его график

15.10

Закрепление полученных знаний

Нахождение решений линейного уравнения с двумя переменными

практическая работа

Презентация

22

Линейное уравнение с двумя переменными и его график

16.10

Практическое занятие

Контроль полученных ЗУН

Построение графика линейного уравнения с двумя переменными

индивидуальная

фронтальная

Проверочная работа

23

Линейная функция и ее график

20.10

Изучение нового материала.

Понятия

наибольшее и

наименьшее

значение

функции, символ

принадлежности

строить графики уравнения с двумя переменными и линейной функции, находить значение функции, заданной формулой, таблицей, графиком по её аргументу, находить значение аргумента по значению функции, заданной графиком или таблицей.

- понимать функцию как важнейшую математическую модель для описания процессов и явлений окружающего мира.

Лекция

индивидуальная

Презентация Задания для индивидуальной работы

24

Линейная функция и ее график

22.10

Закрепление полученных знаний

семинар

фронтальная

Презентация

25

Линейная функция и ее график

23.10

Систематизация и обобщение

индивидуальная

фронтальная

Проверочная работа

26

Линейная функция у= kx

5.11

Изучение нового материала.

Прямая пропорциональность, прямопропорциональные

величины

Уметь строить и читать график функции у=кх

индивидуальная

семинар

Задания для индивидуальной работы

27

Взаимное расположение графиков линейных функций

6.11

Изучение нового материала.

Закрепление полученных знаний

Автоматизм распознавания графиков линейной функции

ax+by=c, где а≠0 или b≠0, при различных а, b,с.

Строить график линейной функции, описывать ее свойства на основе графических представлений. Показывать схематически положение на координатной плоскости графиков функций y=kx, y=kx+b, в зависимости от значений коэффициентов.

Групповая

практическая работа

Презентация Таблица

28

Контрольная работа №2

10.11

Контроль ЗУН

линейная функция, график линейной функции, наибольшее значение линейной функции, наименьшее значение линейной функции, возрастание, убывание, угловой коэффициент.

индивидуальная

Контрольная работа

Презентация Таблица

III.

Системы двух линейных уравнений с двумя переменными

12 часов

Задания для индивидуальной работы

29

Основные понятия

12.11

Изучение нового материала.

Понятия: решение системы; несовместная система; неопределенная система

индивидуальная

фронтальная

30

Основные понятия

13.11

Закрепление полученных знаний

Решать системы двух линейных уравнений с двумя переменными графически, методом подстановки, методом алгебраического сложения.

Решать текстовые задачи алгебраическим способом: переходить от словесной формулировки условия задачи к алгебраической модели путем составления системы уравнений; решать составленную систему уравнений; интерпретировать результат.

Исследовать системы уравнений с двумя переменными, содержащие буквенные коэффициенты.

Конструировать эквивалентные речевые высказывания с использованием алгебраического и геометрического языков.

Использовать функционально-графические представления для решения и исследования систем уравнений.

групповая

Самостоятельная работа

Презентация

31

Метод подстановки

17.11

Изучение нового материала.

Алгоритм решения системы двух уравнений с двумя переменными методом подстановки

индивидуальная

фронтальная

32

Метод подстановки

19.11

Закрепление полученных знаний

практическая работа

Презентация

33

Метод подстановки

20.11

Закрепление практических умений

индивидуальная

фронтальная

Самостоятельная работа

Задания для индивидуальной работы

34

Метод алгебраического сложения

24.11

Изучение нового материала.

Алгоритм решения системы двух уравнений с двумя переменными методом сложения

лекция

семинар

Устный опрос по теории

Задания для

индивидуальной работы

35

Метод алгебраического сложения

26.11

Закрепление полученных знаний

индивидуальная

фронтальная

Устный опрос по теории

Презентация

36

Метод алгебраического сложения

27.11

Контроль изученного материала

индивидуальная

фронтальная

Самостоятельная работа

37

Системы двух линейных уравнений с двумя переменными как математические модули реальных ситуаций

1.12

Изучение нового материала.

Выработать умение решать системы уравнений и применять их при решении текстовых задач;

индивидуальная

семинар

Задания для индивидуальной работы

38

Системы двух линейных уравнений с двумя переменными как математические модули реальных ситуаций.

Закрепление.

3.12

Закрепление полученных знаний

практическая работа

Презентация

39

Системы двух линейных уравнений с двумя переменными как математические модули реальных ситуаций.

4.12

Закрепление полученных знаний

индивидуальная

Самостоятельная работа

40

Системы двух линейных уравнений с двумя переменными как математические модули реальных ситуаций.

8.12

Обобщение и систематизация знаний

групповая

Самостоятельная работа

Презентация

41

Контрольная работа №3

10.12

Контроль ЗУН

Методы решения систем двух линейных уравнений с двумя переменными и уметь применять их для решения задач

решать системы двух линейных уравнений с двумя переменными тремя способами (графическим, подстановкой, сложением),

Применять при решении текстовых задач

индивидуальная

Контрольная работа

Задания для индивидуальной работы

IV

Степень с натуральным показателем 6 часов

Задания для индивидуальной работы

42

Что такое степень с натуральным показателем

11.12

Изучение нового материала.

понятия: степень, основание степени, показатель степени.

- возводить числа в степень; -заполнять и оформлять таблицы, отвечать на вопросы с помощью таблиц

индивидуальная

фронтальная

Устный опрос по теории

43

Таблицы основных степеней

15.12

Изучение нового материала.

Закрепление изученного материала

Степени числа 2, степени числа 3, степени числа 5, степени числа 7, степени составных чисел

- пользоваться таблицей степеней при выполнении вычислений со степенями;

- участвовать в диалоге, понимать точку зрения собеседника, подбирать аргументы для ответа на поставленный вопрос, приводить примеры

групповая

Таблица степеней чисел 2 и 3.

Опорный конспект

44

Свойства степени с натуральным показателем

17.12

Изучение нового материала.

Свойства степени с натуральным показателем; теоремы 1-3 и их доказательства.

Уметь осуществлять проверку выводов, положений, закономерностей, теорем

практическая работа

Задания для индивидуальной работы

45

Свойства степени с натуральным показателем

18.12

Закрепление изученного материала

• применять св-ва степеней для упрощения числовых и алгебраических выражений;

• аргументировано отвечать на поставленные вопросы, осмыслить ошибки и устранить их;

-развернуто обосновывать суждение

индивидуальная

фронтальная

Самостоятельная работа

Презентация Таблица степеней чисел

46

Умножение и деление степеней с одинаковыми показателями

22.12

Изучение нового материала.

Закрепление изученного материала

правила умножения и деления степеней с одинаковыми показателями; как применять эти правила при вычислениях, для преобразования алгебраических выражений.

определять понятия, приводить доказательства

применять правила умножения и деления степеней с одинаковыми показателями для упрощения числоэых и алгебраических выражений; - пользоваться энциклопедией, математическим справочником, записанными правилами

индивидуальная

фронтальная

Таблица степеней чисел

47

Степень с нулевым показателем

24.12

Изучение нового материала.

Правила действий над степенями с одинаковыми показателями

- находить степень с натуральным показателем;

- находить степень с нулевым показателем;

- работать по за-

данному алгорит-

му, доказывать

правильность ре-

шения с помощью

аргументов

семинар

Самостоятельная работа

Презентация Задания для индивидуальной работы

V

Одночлены. Арифметические операции над одночленами

8 часов

Таблица степеней чисел

48

Понятие одночлена. Стандартный вид одночлена

25.12

Изучение нового материала.

Закрепление изученного материала

Понятие одночлена. Его коэффициент, буквенная часть, стандартный вид..

находить значение одночлена при указанных значениях переменных; вступать в речевое общение, участвовать в диалоге

индивидуальная

фронтальная

49

50

Сложение и вычитание одночленов

12.1

Изучение нового материала.

Закрепление изученного материала

Определение подобных одночленов. Алгоритм сложения и вычитания одночленов

воспроизводить прочитанную информацию с заданной степенью свернутости, правильно оформлять решения, выбрать из данной информации нужную

индивидуальная

семинар

Презентация Задания для индивидуальной работы

Презентация Задания для индивидуальной работы

Презентация

практическая работа

индивидуальная

Самостоятельная работа

14.1

51

Умножение одночленов. Возведение одночлена в натуральную степень

15.1

Изучение нового материала.

Основные определения и правила умножения многочленов.

проводить информационно-смысловой анализ прочитанного текста, составлять конспект, участвовать в диалоге

индивидуальная

фронтальная

Устный опрос по теории

52

Умножение одночленов. Возведение одночлена в натуральную степень

19.1

Закрепление изученного материала

- применять правила умножения одночленов, возведения одночлена в степень для упрощения выражений; - воспроизводить изученную информацию с заданной степенью свернутости, подбирать аргументы, соответствующие решению, правильно оформлять работу

групповая

Устный опрос по теории

Презентация

53

Деление одночлена на одночлен

21.1

Изучение нового материала.

Основные определения и правила деления

многочленов.

- выполнять деление одночленов по алгоритму;

- применять правило деления одночленов для упрощения алгебраических дробей;

- аргументированно отвечать на поставленные вопросы, осмысливать ошибки и устранять их

практическая работа

54

Деление одночлена на одночлен.

22.1

Закрепление изученного материала

- применять правило деления одночленов для упрощения алгебраических дробей;

индивидуальная

фронтальная

Самостоятельная работа

Задания для индивидуальной работы

55

Контрольная работа №4

26.1

Контроль ЗУН

Основные определения и правила сложения, вычитания, умножения и деления многочленов.

-расширять

и обобщать знания

об арифметических

операциях над одночленами;

- предвидеть возможные последствия своих действий

индивидуальная

контрольная работа

VI

Многочлены. Арифметические операции над многочленами

15 часов

Презентация

56

Основные понятия

28.1

Понятие многочлена, его старшего члена и степени

Отработка умений и навыков

Умения выполнять операции с многочленами . Иметь представле-

ние о многочлене,

о действии приведения подобных членов многочлена, о стандартном виде многочлена, о полиноме.

выбрать и выполнить задание по своим силам и знаниям, применить знания для решения практических задач

лекция

индивидуальная

фронтальная

Презентация

57

Сложение и вычитание многочленов

29.1

Изучение нового материала.

Правила сложения и вычитания многочленов

- выполнять сложение и вычитание многочленов; воспринимать устную речь, проводить информационно-смысловой анализ лекции, приводить и разбирать примеры, участвовать в диалоге

индивидуальная

фронтальная

Матем. диктант

Задания для индивидуальной работы

58

Сложение и вычитание многочленов

2.2

Закрепление изученного материала

индивидуальная

семинар

Самостоятельная работа

Презентация

59

Умножение многочлена на одночлен

4.2

Изучение нового материала.

Правила умножения многочлена на одночлен

- выполнять умножение многочлена на одночлен, выносить за скобки одночленный множитель.

- отражать в письменной форме свои решения, формировать умения рассуждать, выступать с решением проблемы

в письменной форме свои решения,

рассуждать и обобщать, участвовать в диалоге, выступать с решением проблемы

практическая работа

60

Умножение многочлена на одночлен

5.2

Закрепление изученного

индивидуальная

Самостоятельная работа

Презентация

61

Умножение многочлена на многочлен

9.2

Изучение нового материала.

Правила умножения многочлена на многочлен

- выполнять умно-

жение многочленов; - воспринимать устную речь, участвовать в диалоге, аргументированно рассуждать и обобщать, приводить примеры

индивидуальная

фронтальная

62

Умножение многочлена на многочлен.

11.2

Закрепление изученного материала

- решать текстовые

задачи, математическая модель которых содержит произведение мно-

гочленов;

- рассуждать и обобщать, подбирать аргументы, соответствующие решению, участвовать в диалоге

групповая

Задания для индивидуальной работы

63

Умножение многочлена на многочлен.

12.2

Закрепление практических умений

практическая работа

Тест

Презентация

64

Формулы сокращенного умножения

16.2

Изучение нового материала.

Иметь представле-

ние о формулах

квадрата суммы

и разности, разно-

сти квадратов

и кубов, суммы

кубов; о геометри-

ческом обоснова-

нии этих формул.

воспроизводить прослушанную

и прочитанную

информацию

с заданной степенью

свернутости

индивидуальная

фронтальная

Задания для индивидуальной работы

65

Формулы сокращенного умножения

18.2

Изучение нового материала.

Формула квадрата разности и квадрата суммы. Знать, как выпол-

нять преобразова-

ния многочленов,

вычисления по

формулам

проводить

анализ данного за-

дания, аргументи-

ровать решение,

презентовать

решения

индивидуальная

фронтальная

Диктант

Задания для индивидуальной работы

66

Формулы сокращенного умножения

19.2

Изучение нового материала.

Закрепление практических умений

Формула разности квадратов

- выполнять преобразования многочленов, вычисления по формулам квадрата суммы и разности, разности квадратов и кубов, суммы кубов;

- подбирать аргументы, соответствующие решению, формировать умения работать по заданному алгоритму, сопоставлять

семинар

Самостоятельная работа

Презентация

67

Формулы сокращенного умножения

25.2

Изучение нового материала.

Формула разности кубов и суммы кубов

лекция

индивидуальная

фронтальная

Задания для индивидуальной работы

68

Формулы сокращенного умножения

26.2

Закрепление практических умений

Формула разности кубов и суммы кубов

применять формулы сокращённого умножения для упрощения выражений, решения уравнений; - использовать данные правила и формулы, аргументировать решение, правильно оформлять работу

индивидуальная

фронтальная

Зачет

Презентация

69

Деление многочлена на одночлен

2.3

Изучение нового материала.

Закрепление практических умений

Правила деления многочлена на одночлен

- использовать правило деления многочлена на одночлен для упрощения выражений, решения уравнений;

-отражать в письменной форме свои решения, применять знания предмета в жизненных ситуациях, выступать с решением проблемы

индивидуальная

семинар

Тест

Задания для индивидуальной работы

70

Контрольная работа №5

4.3

Контроль ЗУН

ФСУ

- расширять и обобщать знания о сложении, вычитании, умножении и делении многочленов, вывода и применения формул сокращенного умножения;

-владеть навыками контроля и оценки своей деятельности

индивидуальная работа

контрольная работа

VII

Разложение многочленов на множители 18 часов

Презентация

71

Что такое разложение многочленов на множители и зачем оно нужно?

5.3

Изучение нового материала.

Необходимость умения раскладывать многочлен на множители для решения уравнений и других задач математики

Иметь представление о корнях уравнения, о сокращении дробей, о разложении многочлена на множители.

Уметь подбирать аргументы для доказательства своей точки зрения.

индивидуальная

фронтальная

Презентация

72

Вынесение общего множителя за скобки

11.3

Изучение нового материала.

Закрепление изученного материала

Алгоритм разложения многочлена на множители путем вынесения за скобки общего множителя

Уметь выполнять вынесение общего множителя за скобки по алгоритму, рассуждать, обобщать.

групповая

Задания для индивидуальной работы

73

Вынесение общего множителя за скобки

12.3

Закрепление практических умений

Уметь применять приём вынесения общего множителя за скобки для упрощения вычислений, решения уравнений; рассуждать, обобщать, находить несколько решений одной задачи.

практическая работа

Самостоятельная работа

Презентация

74

Способ группировки

16.3

Изучение нового материала.

Закрепление изученного материала

Метод разложения многочлена на множители способом группировки

Применять алгоритм разложения многочлена на множители способом группировки.

Уметь аргументировано рассуждать, обобщать.

индивидуальная

фронтальная

Задания для индивидуальной работы

75

Способ группировки.

18.3

Закрепление изученного материала

Уметь выполнять разложение многочлена на множители способом группировки по алгоритму.

индивидуальная

фронтальная

Самостоятельная работа

Презентация

76,

77

Разложение многочлена на множители с помощью формул сокращенного умножения. (Квадрат разности и квадрат суммы)

19.3

Изучение нового материала.

Закрепление изученного материала

Метод разложения

многочлена на

множители с

помощью формул

сокращенного

умножения

Уметь применять приём разложения многочлена на множители с помощью формул сокращённого умножения для упрощения вычислений и решения уравнений.

Воспринимать устную речь, проводить информационно-смысловой анализ. Уметь воспроизводить полученную информацию с заданной степенью точности и свёрнутости.

лекция

индивидуальная

Задания для индивидуальной работы

Задания для индивидуальной работы

Задания для индивидуальной работы

30.3

фронтальная

индивидуальная

Самостоятельная работа

78

Разложение многочлена на множители с помощью формул сокращенного умножения.( Разность квадратов)

1.4

Изучение нового материала.

Закрепление изученного материала

индивидуальная

семинар

Презентация

79

Разложение многочлена на множители с помощью формул сокращенного умножения. (Разность кубов и сумма кубов)

2.4

Изучение нового материала.

Закрепление изученного материала

практическая работа

Самостоятельная работа

80

Разложение многочлена на множители с помощью формул сокращенного умножения.

6.4

Обобщение и систематизация полученных навыков

индивидуальная

Самостоятельная работа

Задания для индивидуальной работы

81

Разложение многочленов на множители с помощью комбинации различных приёмов

8.4

Изучение нового материала.

Обработка практических умений и навыков

Комбинирован

ные приемы для разложения многочлены на множители

Уметь выполнять разложение многочлена на множители с помощью комбинированных приёмов: вынесение за скобки общего множителя, формулы сокращённого умножения, способ группировки, метод выделения полного

индивидуальная

фронтальная

Устный опрос по теории

Презентация

82

Разложение многочленов на множители с помощью комбинации различных приёмов

9.4

Закрепление практических умений

Комбинирован

ные приемы для разложения многочлены на множители

групповая

83

Разложение многочленов на множители с помощью комбинации различных приёмов

13.4

Обработка практических умений и навыков

Комбинированные приемы для разложения многочлены на множители

практическая работа

84

Сокращение алгебраических дробей

15.4

Изучение нового материала.

Понятие алгебраической дроби. Иметь представление об алгебраической дроби, числителе и знаменателе алгебраической дроби, о сокращении алгебраических дробей.

Уметь рассуждать, обобщать, систематизировать.

индивидуальная

фронтальная

85

Сокращение алгебраических дробей.

16.4

Закрепление изученного материала

Понятие алгебраической дроби. Возможность сокращения алгебраических дробей

Уметь сокращать алгебраические дроби, раскладывая выражения на множители, применяя формулы

индивидуальная

фронтальная

Задания для индивидуальной работы

86

Сокращение алгебраических дробей.

20.4

Закрепление практических умений

Понятие алгебраической дроби. сокращение алгебраических дробей

Уметь применять различные способы разложения многочлена на множители при сокращении алг. дробей.

семинар

87

Тождества

22.4

Изучение нового материала.

Закрепление практических умений

Понятия: тождество, тождественно равные выражения, тождественное преобразование, допустимые значения переменной

Уметь пользоваться основными алгоритмическими приемами доказательства тождества - научиться выполнять многошаговые преобразования рациональных выражений, применяя широкий набор способов и приемов;

- применять тождественные преобразования для решения задач из различных разделов курса.

лекция

индивидуальная

фронтальная

Самостоятельная работа

Презентация.

Таблица с графиками

у = х²

88

Контрольная работа №6

23.4

Контроль ЗУН

Уметь пользоваться основными алгоритмическими приемами доказательства тождества и сокращения дробей

индивидуальная

фронтальная

Контрольная работа

Таблица с графиками

у = х²

VIII

Функция у = х²

Таблица с графиками

у = х²

89

Функция у = х² и ее график

27.4

Изучение нового материала.

Квадратичная функция у = х²

Уметь строить и читать график функцииу=х²

практическая работа

Самостоятельная работа

Презентация.

Таблица с графиками

у = х²

90

Функция у = х² и ее график

29.4

Закрепление практических умений

индивидуальная

Устный опрос по теории

Таблица с графиками

у = х²

91

Функция у = х² и ее график

30.4

Закрепление практических умений

индивидуальная

фронтальная

Таблица с графиками

у = f(х)

92

Графическое решение уравнений

4.5

Изучение нового материала.

Закрепление

Алгоритм графического решения уравнений

Уметь решать уравнения графическим способом

групповая

Таблица с графиками

у = f(х)

93

Графическое решение уравнений

6.5

Закрепление практических умений

Уметь решать уравнения графическим способом

практическая работа

Самостоятельная работа

Задания для индивидуальной работы

94

Что означает в математике запись

у = f(х)

7.5

Изучение нового материала.

Понятия: функция у = f(х), независимая переменная х и зависимая переменная у, значение функции, область определения функции

Знать функциональную символику, читать графики

индивидуальная

фронтальная

95, 96

Что означает в математике запись

у = f(х)

11.5

Закрепление практических умений

Понятия: функция у = f(х), независимая переменная х и зависимая переменная у, значение функции, область определения функции

индивидуальная

фронтальная

семинар

Устный опрос по теории

Тест

Задания для индивидуальной работы

13.5

97

Контрольная работа №7

14.5

Контроль ЗУН

работать с графическими моделями,

читать и строить график функции у=х²

индивидуальная

Контрольная работа

IX

Итоговое повторение

Задания для индивидуальной работы

98

Решение задач

18.5

Закрепление практических умений

индивидуальная

фронтальная

99

Линейная функция

20.5

Закрепление практических умений

практическая работа

Задания для индивидуальной работы

100

Системы линейных уравнений. Решение задач.

21.5

Закрепление практических умений

индивидуальная

Самостоятельная работа

101

Степень с натуральным показателем. Одночлены, действия с одночленами.

25.5

Закрепление практических умений

индивидуальная

фронтальная

Задания для индивидуальной работы

102

Многочлены . Операции над многочленами.

27.5

Закрепление практических умений

групповая

103

Формулы сокращенного умножения.

28.5

Закрепление практических умений

практическая работа

Самостоятельная работа

104

Разложение многочленов на множители.

Закрепление практических умений

индивидуальная

фронтальная

105

Итоговая контрольная работа (экзамен)

Контроль ЗУН

индивидуальная

контрольная работа