Использование частично-поискового метода при формировании навыков прикладного использования аппарата производной.

Тема урока Применение производной при исследовании функций..

Тип урока: урок сообщения новых знаний.

Форма урока: урок - практикум.

Оборудование: компьютер, проектор, экран, интерактивная доска.

Цели и задачи урока:

Учебная цель.

Обобщение, систематизация и углубление знаний о производной. Формирование навыков прикладного использования аппарата производной. Овладение умениями и навыками нахождения промежутков возрастания и убывания, экстремумов функции.

Развивающая цель.

Развитие умений в применении знаний в конкретной ситуации; самостоятельной деятельности учащихся.

Развитие мыслительных способностей, обеспечивающих анализ ситуации и разработку адекватных способов действия (анализ, синтез, сравнение).

Воспитательная цель.

Воспитывать такие качества личности, как познавательная активность, самостоятельность, упорство в достижении цели. Побуждать учащихся ко взаимоконтролю, самоанализу своей деятельности.

Задачи.

• организовать деятельность учащихся по применению достаточных условий возрастания и убывания функции к нахождению промежутков монотонности функции;

• организовать частично-поисковую деятельность учащихся при формулировании необходимого и достаточного признака экстремума функции;

• научить применять производную для реализации схемы исследования функции.

План

1. Организационный этап (вступительное слово преподавателя)….3 мин

2. Устные упражнения. Актуализация ранее изученного……..….. 15 мин

3. Сообщение темы урока…………………………….……….……….5 мин

4. Объяснение нового материала……………………………………..20 мин

5. Первичное закрепление…….……………………………………….15 мин

6. Самостоятельное решение задач..…………………………………..15 мин

7. Подведение итогов……………………………………………………5 мин

8. Этап рефлексии…………………………………………………..….. 2 мин

1. Организационный момент

Цель деятельности педагога: проверить готовность к занятию, настроить на выполнение учебных задач.

Цель деятельности учащегося: настроиться на учебный процесс, проверить свою готовность к занятию.

Вступительное слово преподавателя: Сегодня мы продолжаем изучать приложение производной и рассмотрим вопрос о её применении к исследованию функций.

Производная применяется при описании различных, в частности экономических процессов. Чтобы изучить любой процесс необходимо пройти следующие этапы:

1. Этап построения математической модели. Одну изучаемую величину (прибыль, расходы на производство и т.п.) обозначают у; другую величину (цену товара, величину спроса, объём производства и т.п.) считают независимой переменной и обозначают х. Исходя из конкретных условий задачи, выражаю у через х.

2. Этап исследования модели. Для полученной функции находят максимум (минимум) на промежутке реального изменения х.

3. Этап интерпретации результата.

2. Актуализация ранее изученного.

Цель деятельности педагога: актуализировать знания, необходимые для изучения темы, развивать позитивный интерес к предмету.

Цель деятельности учащегося: поверить в свои силы, оказавшись в ситуации успеха при решении известных задач.

Слово преподавателя: Сегодня на уроке мы рассмотрим элемент работы второго этапа изучения процесса, исследование одного из свойств функции - определение промежутков монотонности и экстремумов функции.

Для решения поставленной задачи, нам необходимо вспомнить некоторые вопросы, рассмотренные ранее.

Проводится фронтальный опрос (рисунки на слайдах).

1. Что называется функцией?

2. Какая функция называется возрастающей на промежутке?

3. Какая функция называется убывающей на промежутке?

4. Укажите на рисунке промежутки возрастания (убывания) функции.

5. В чём заключается геометрический смысл производной?

6. На рисунке изображены график функции 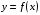и касательная к нему в точке с абсциссой 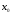. Найдите значение производной функции 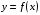в точке .

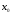7. Укажите, из каких отмеченных точек 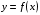, 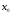и

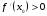
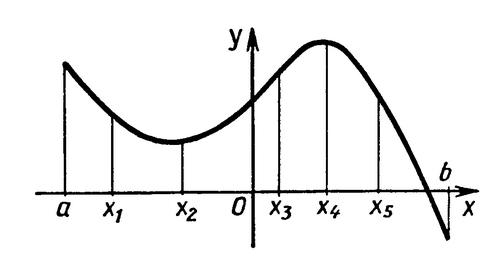
3. Сообщение темы урока.

Цель деятельности педагога: поставить конкретную учебную цель перед учащимися; поместить учащихся в ситуацию успеха, показав, что они сами «открыли» то, с чем должны познакомиться на уроке.

Цель деятельности учащегося: поверить в свои силы, оказавшись в ситуации успеха при решении известных задач.

Слово преподавателя: Попробуем теперь применить имеющиеся у нас знания для определения промежутков возрастания и убывания функции.

4. Объяснение нового материала.

у

х

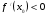
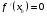
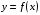
- На рисунке изображён график функции . В произвольных точках интервала 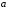проведём касательные к графику этой функции. Обратите внимание на угол, который образуют касательные с положительным направлением оси ОХ. Какой вывод можно сделать о знаке углового коэффициента касательной, а значит и производной?

Примерные ответы учеников: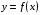

-

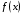
х

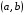
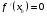
у

Рассмотрим теперь график убывающей функции.

Какой вывод можно сделать о знаке углового коэффициента касательной, а значит и производной?

Примерные ответы учеников: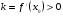

- Какая связь между знаком производной и поведением функции выявлена на примере этих заданий?

Примерные ответы учеников: Если на промежутке 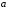производная функции , то функция возрастает, если 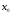, то функция убывает.

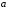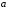- Можно ли сформулировать вывод «наоборот» - если функция возрастает на промежутке , то для всех точек интервала и, если функция убывает на промежутке , то 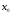для всех точек интервала.

Ответы учеников могут быть различны.

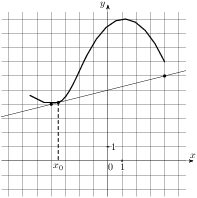
х₀

х

у

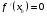
Учитель: обратное - неверно. Посмотрите на график функции на рисунке. На всём интервале 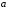функция возрастает, но в точке х₀ производная 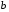(касательная в этой точке параллельна оси ОХ), а значит нельзя сказать, что на всём интервале производная положительна. Поэтому признак, который мы сформулировали - достаточный.

Запишем в тетрадь:

Достаточный признак возрастания (убывания) функции:

Если в каждой точке интервала I, то функция 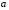возрастает на I.

Если 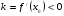в каждой точке интервала I, то функция 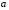убывает на I.

Мы рассмотрели поведение функции на промежутках, где и 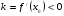. А что же будет в точках, где производная равна нулю или не существует?

Примерные ответы учеников: в этих точках будут экстремумы, т.к. в экстремумах касательная параллельна оси Ох.

Слово преподавателя: Эти точки могут быть точками экстремума, поэтому их называют критическими или подозреваемыми на экстремум. Равенство нулю производной - необходимое условие экстремума.

Запись в тетради:

Необходимое условие экстремума. Если точка х₀ является точкой экстремума функции 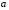и в этой точке существует производная, то она равна нулю, .

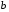Учащиеся получают раздаточный материал - незаполненные таблицы с графиками функций. Работая в парах, заполняют пустые клетки.

Знак 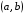на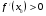

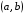
в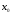

Знак 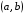на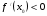

Вывод

о точке

1

х₀

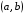
у

х

-

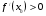
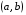
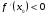
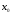точка

максимума

2

х₀

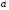
х

у

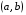
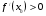
не существует

-

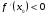
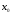точка

максимума

3

х

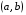
х₀

у

-

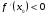
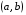
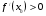
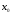точка

минимума

4

х₀

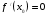
х

у

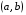
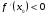
не существует

-

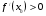
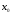точка

минимума

5

х₀

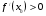
х

у

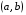
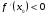
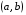
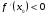
нет

экстремума

6

х₀

х

у

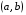
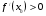
не существует

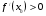
нет

экстремума

Слово преподавателя: Проанализируем поведение функции в точке х₀. Какое же условие должно выполняться, чтобы точка была точкой экстремума?

Примерные ответы учеников: нужно, чтобы производная меняла свой знак при переходе через х₀.

Признак максимума функции: Если функция f непрерывна в точке х₀ и производная при переходе через эту точку меняет знак с «+» на «-», то точка х₀ является точкой максимума функции.

Признак минимума функции: Если функция f непрерывна в точке х₀ и производная при переходе через эту точку меняет знак с «-» на «+», то точка х₀ является точкой минимума функции.

Алгоритм нахождения промежутков монотонности и экстремумов.

1. Найти производную функции .

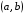2. Найти критические точки функции 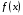(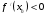или не существует).

3. Отметить критические точки на числовой прямой и определить знаки производной на получившихся промежутках.

4. Сделать выводы о промежутках возрастания и убывания функции.

5. Сделать вывод о точках экстремума.

5. Первичное закрепление.

Пример 1. Найдите промежутки возрастания и убывания функции .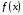

Решение: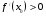

-

-

+

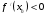
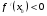
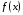
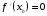
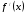
- 1

2

min

max

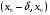
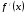
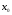
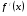
Пример 2. Найдите промежутки возрастания и убывания функции .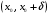

6. Самостоятельное решение задач.

Учащиеся работают в парах, решение записывают в тетрадях. Двое работают у доски.

а) ;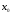

б) ;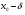

а)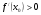

б)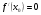

7. Подведение итогов.

Цель деятельности педагога: анализ реализации поставленной цели и задач.

Цель деятельности учащегося: провести анализ своего вклада в работу группы по решению поставленных задач; оценить свою работу и работу товарищей.

Слово преподавателя: Ребята, сегодня мы научились строить сечения. Как? Покажут результаты самостоятельной работы. Вы сами сможете оценить себя. Полученные умения помогут в дальнейшем решать различные геометрические задачи.

Проверка самостоятельной работы учащимися (правильные решения на слайдах). Студенты подсчитывают количество ошибок и выставляют себе оценку за работу на уроке согласно представленным критериям:

«5» - нет ошибок;

«4» - одна-две ошибки;

«3» - более двух ошибок.

8. Рефлексия урока.

Цель деятельности педагога: создание условий для саморазвития, самопознания школьника.

Цель деятельности учащегося: воспроизведение полученных в ходе занятия знаний; осознание собственной деятельности.

Слово преподавателя:

1. Какими навыками, умениями вы овладели на сегодняшнем уроке?

2. Что было непонятно?

3. Решение каких задач показалось вам сложным?

4. Какие задания вам понравились?

5. Что удивило вас?