Урок математики в 11 классе по теме 'Методы решения показательных уравнений'

Конспект открытого урока по математике в 11 классе по технологии деятельного подхода.

Тема урока «Методы решения показательных уравнений»

Учитель математики Шагдарова Дулма Гончиковна, МОУ «М СОШ № 3».

Эпиграф: Ум человеческий имеет три ключа, все открывающих: знание, мысль, воображение»

В.Гюго.

Тип урока: изучение нового материала

Оборудование: проектор, компьютер, карточки, лист контроля.

Формы работы: индивидуальная, работа в группах, коллективная.

Цель урока: развитие ключевых компетентностей учащихся посредством самостоятельного приобретения знаний путём творческого поиска и решения проблемных вопросов и ситуаций.

Задачи:

1. Образовательная: продолжить работу над формированием алгоритмов решения показательных уравнений; обеспечить повторение свойств степени, необходимых для их решения.

2. Развивающая: способствовать формированию умений применять различные приёмы: сравнение, выделение главного, переноса знаний в новую ситуацию, также развитию математического кругозора, логического мышления, устной речи и внимания.

3. Воспитательная: содействовать развитию мотиваций и самосовершенствования личности учащегося.

Ход урока:1.Самоопределение к деятельности.

2.Актуализация знаний и фиксация затруднений в деятельности.

3.Постановка учебной задачи.

4. Построение проекта выхода из затруднения детьми.

5.Первичное закрепление во внешней речи.

6.Самостоятельная работа с самопроверкой .

7.Включение в систему знаний и повторение.

8.Рефлексия деятельности.

1.Цель этапа: Слайд-1. знание

Эпиграф: Ум человеческий имеет три ключа, все открывающих: мысль

воображение»

В.Гюго.

а) настроить учащихся на учебную деятельность.

б) напомнить правила поведения в группе.

2.Актуализация знаний:

Цель этапа:

а) актуализировать знания, необходимые для восприятия нового материала.

б) консультантам в группе зафиксировать индивидуальные затруднения в деятельности у товарищей.

Слайд-2 Игра «Подумай- победи»

Участвуют все группы, выигрывает группа, решившая все примеры правильно.

Ответы : показатель

Слайд-3 Задание 2 . Решить уравнения.

Что общего в этих уравнениях?

Сформулируйте определение показательных уравнений.

Цель этапа: а) организовать взаимодействие в группах для обсуждения и построения нового способа действия, устраняющего причину выявленного затруднения.

б) зафиксировать новый способ действия в знаковой, вербальной форме.

Вернуться к уравнениям второго задания назвать методы решения показательных уравнений.

Слайд-4: Данные уравнения попробуйте классифицировать по методу решения.

1. ;(1б) 11. ;(3б)

2. ; (1б) 12. ;(2б)

3. ( (2б) 13. ;(2б)

4. ; (2б) 14. ;(1б)

5. ;(1б) 15. ;(2б)

6. (1б) 16. ;(1б)

7. (1б) 17. (1б)

8. (2б) 18. ;(2б)

9. 3*; (3б) 19. ;(1б)

10. ; (1б) 20. ;(3б)

Слайд-5.

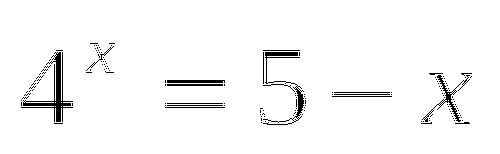
• Учащиеся проверяют результаты групповой работы. Разбираем, примеры, где есть разногласия, согласовываем результаты.

• Затем каждая группа вытягивает карточку с названием метода и стараются составить на свой метод алгоритм решения показательного уравнения, для защиты один представитель от группы через решение уравнения раскрывает алгоритм метода решения уравнения (приложение 3).

Самостоятельная работа.

• Ученики выбирают из данных уравнений по 2-3 примера,

Решают, самоконтроль, проверят через готовые ответы, оценивают свои результаты.

Слайд-6.

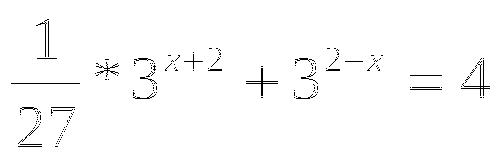
Цель этапа: проверить умение применять новое учебное содержание в типовых условиях.

Рефлексия: а) оценить работу в группе.

б) отметить наиболее активных членов группы.

в) оценить собственную деятельность на уроке (приложение-2).

Слайд-7.

Приложение-1

Показательные уравнения

1. ;(1б) 11. ;(3б)

2. ; (1б) 12. ;(2б)

3. (2б) 13. ;(2б)

4. ; (2б) 14. ;(1б)

5. ;(1б) 15. ;(2б)

6. (1б) 16. ;(1б)

7. (1б) 17. (1б)

8. (2б) 18. ;(2б)

9. 3*; (3б) 19. ;(1б)

10. ; (1б) 20. ;(3б)

Приложение-2

Приложение №3.

Алгоритм графического метода:

1.Каждую часть уравнения рассматривать как функцию.

2.Выяснить монотонность функции.

3.Построить графики данных функций в одной координатной плоскости.

4.Абсцисса точки пересечения графиков - решение уравнения.

Алгоритм метода уравнивания показателей:

1.Левую и правую часть уравнения записываем с одинаковым основанием (алгебраические преобразования, свойства степени).

2.По теореме приравниваем показатели и решаем полученное уравнение.

Алгоритм метода введения новой переменной:

1.Если нужно делаем преобразования, получаем в показателе 2х и х.

2.Заменить выражение, содержащее переменную в показателе на новую переменную.

3. Решить полученное квадратное уравнение.

4.Найденные корни приравниваем к выражениям, находим корни показательных уравнений.

Литература:

1.А.Г.Мордкович Алгебра и начала математического анализа. 11 класс.(профильный уровень).Москва,2010.Издательство «Мнемозина»

2.А.Н.Рурукин Контрольно-измерительные материалы.Москва,2011. ВАКО.

3.Л.А.Александрова Самостоятельные работы по алгебре 11 класс.Москва,2011Издательство «Мнемозина»

4.Материалы ЕГЭ с 2004-2012 годы.