- Учителю
- Конспект урока по теме: «Решение систем неравенств с одной переменной» (8 класс)
Конспект урока по теме: «Решение систем неравенств с одной переменной» (8 класс)
Конспект урока по теме: «Решение систем неравенств с одной переменной»
Класс: 8.
Тип урока: усвоение новых знаний.
Цели:
-
Образовательные:
-
Рассмотреть понятие системы неравенств с одной переменной.
-
Дать определение решения системы неравенств с одной переменной.
-
Определить, что значит решить систему неравенств.
-
Научить решать системы неравенств с одной переменной.
-
Воспитательные:
-
Воспитание дисциплинированности.
-
Воспитание интереса к изучению материала.
-
Воспитание культуры общения.
-
Развивающие:
-
Развитие внимания, логического мышления, сообразительности.
-
Развитие математической речи учащихся.
-
Развитие памяти, элементов творческой деятельности.
Структура урока:
-
Организационный момент (1 мин).
-
Постановка целей и задач на урок (1 мин).
-
Анализ самостоятельной работы (7 мин).
-
Формирование новых знаний и умений (15 мин).
-
Закрепление новых знаний и умений (15 мин).
-
Задание на дом (2 мин).
-
Подведение итогов (5 мин).
Литература: Алгебра 8 класс, Макарычев Ю.Н. и др.
-
Этапы
Деятельность учителя
Деятельность учащихся
Вид доски
Организационный момент
Здравствуйте, присаживайтесь!
Присаживаются.
Постановка целей и задач на урок
Сегодня мы с вами в начале урока проведем анализ самостоятельной работы, которую вы писали на прошлом уроке, разберем некоторые ваши ошибки. Затем у нас сегодня изучение новой темы и решение задач по новой теме.
Слушают учителя.
Анализ самостоятельной работы
Итак. Самостоятельную работу, в принципе, написали неплохо, но многие из вас сделали ошибки в последнем задании. Сейчас мы его разберем. задание было следующим: при каких значения переменной имеет смысл выражение :
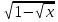 .
. Это выражение имеет смысл, если подкоренное выражение неотрицательно, т.к. арифметический квадратный корень определен только для неотрицательных чисел. То есть
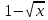
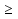 0, и еще должно выполняться одно условие x
0, и еще должно выполняться одно условие x 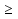 0.
0. Теперь решаем первое неравенство, сначала переносим единицу в право с противоположным знаком, затем умножаем обе части неравенства на минус единицу и меняем знак неравенства на противоположный и возводим обе части неравенства в квадрат. Изображаем на координатной прямой множество решений данных неравенств и записываем ответ. Надеюсь, теперь вам понятно, в чем была ваша ошибка. Если у кого - то есть вопросы по самостоятельной работе, задайте их. Вопросов нет.
Внимательно слушают учителя.
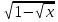
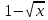
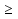 0
0 x
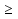 0
0 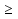
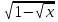 │*(-1)
│*(-1) 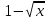 │^2
│^2 x
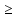 1 и x
1 и x 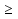 0
0 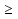
Ответ: x
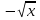 [0; 1].
[0; 1].
Формирование новых знаний и умений
Сейчас мы переходим к изучению новой темы. Открываем тетради, записываем число 15.02.2010 и тему сегодняшнего урока «Решение систем неравенств с одной переменной».
Давайте для начала разберем такую задачу:
Турист вышел из турбазы по направлению к станции, расположенной на расстоянии 20 км. Если турист увеличит скорость на 1 км/ч, то за 4 ч он пройдет расстояние, большее 20 км. Если он уменьшит скорость на 1 км/ч, то даже за 5 ч не успеет дойти до станции. Какова скорость туриста?
Пусть скорость туриста равна x км/ч. Если турист будет идти со скоростью (x+1) км/ч, то за 4 ч он пройдет 4(x+1) км. По условию задачи 4(x+1) > 20. Если турист будет идти со скоростью (x-1) км/ч, то за 5 ч он пройдет 5(x-1) км. По условию задачи 5(x-1) < 20.
Требуется найти те значения x , при которых верно как неравенство 4(x+1) > 20, так и неравенство 5(x-1) < 20, т.е.найти общее решение этих неравенств. В таких случаях говорят, что надо решить систему неравенств, и используют запись
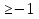
Заменив каждое неравенство системы равносильным ему неравенством, получим систему
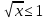
Значит, значение
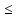 должно удовлетворять условию
должно удовлетворять условию 4 < x < 5.
Ответ: скорость туриста больше 4 км/ч, но меньше 5 км/ч.
Итак. Решением системы неравенств с одной переменной называется значение переменной, при котором верно каждое из неравенств системы.
Решить неравенство - значит найти все его решения или доказать, что решений нет.
Давайте сейчас рассмотрим, как нужно решать системы неравенств с одной переменной.
Пример1: решим систему неравенств
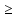
Имеем:
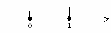
Отсюда
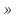
Решениями системы являются значения x , удовлетворяющие каждому их неравенств
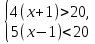 и
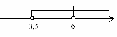
и 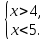 . Изобразив на координатной прямой множество чисел, удовлетворяющих неравенству
. Изобразив на координатной прямой множество чисел, удовлетворяющих неравенству 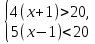 , и множество чисел, удовлетворяющих неравенству
, и множество чисел, удовлетворяющих неравенству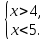 , найдем, что оба неравенства верны при
, найдем, что оба неравенства верны при
15.02.2010 Решение систем неравенств с одной переменной
Пусть скорость туриста равна x км/ч
(x+1)
4(x+1)
4(x+1) > 20
(x-1)
5(x-1) < 20
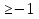
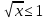
Ответ: скорость туриста больше 4 км/ч, но меньше 5 км/ч.
Пример1
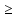
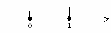
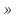
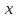
Ответ : x
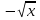 (3,5; 6)
(3,5; 6)
Решение систем неравенств с одной переменной
Пусть скорость туриста равна x км/ч
(x+1)
4(x+1)
4(x+1) > 20
(x-1)
5(x-1) < 20
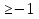
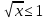
Ответ: скорость туриста больше 4 км/ч, но меньше 5 км/ч.
Пример1
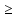
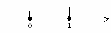
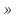
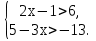
Ответ : x
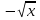 (3,5; 6)
(3,5; 6)
3,5 < x < 6. Множество решений системы есть промежуток (3,5; 6). Ответ можно записать в виде промежутка (3,5; 6) или в виде двойного неравенства 3,5 < x < 6, задающего этот промежуток.
Пример2:решим систему неравенств
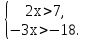
Имеем:
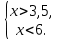
Изобразим на координатной прямой множества решений каждого из неравенств. Оба неравенства верны при
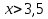 . Ответ можно записать в виде неравенства
. Ответ можно записать в виде неравенства 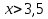 или в виде числового промежутка (9; +
или в виде числового промежутка (9; +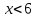 ), задаваемого этим неравенством.
), задаваемого этим неравенством. Пример3: решим систему неравенств
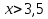
Имеем:
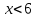
Используя координатную прямую, найдем, что множество чисел, удовлетворяющих неравенству
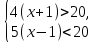 , и множество чисел, удовлетворяющих неравенству
, и множество чисел, удовлетворяющих неравенству 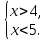 , не имеют общих элементов, т.е. их пересечение пусто. Данная система неравенств не имеет решений.
, не имеют общих элементов, т.е. их пересечение пусто. Данная система неравенств не имеет решений. Ответ: решений нет.
А теперь перейдем к задачам из учебника. открываем учебники на странице187, №874, работаем устно.
Итак, задание следующее: является ли число 3 решением системы неравенств:
а)
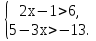
Влад, ответь на этот вопрос.
Правильно, молодец.
б)
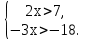
Валера, ответь мне на этот вопрос.
Правильно, молодец.
в)
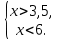
Вика, ответь на этот вопрос.
Правильно, молодец.
Следующий номе это №877, выполняем письменно, кто-то у доски.
Юра, к доске, остальные выполняем в тетради.
Нужно решить систему неравенств.
Молодец, все правильно, присаживайся.
Пример2
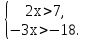
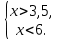
Ответ: x
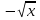 (9; +
(9; +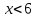 )
) Пример3
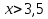
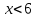
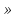
Ответ: решений нет.
Влад: «число 3 является решением системы неравенств, так как при подстановке в данную систему числа 3 мы получаем верное неравенство».
Валера: «число 3 является решением системы неравенств, так как при подстановке в данную систему числа 3 мы получаем верное неравенство».
Вика: «число 3 не является решением системы неравенств, так как при подстановке в данную систему числа 3 мы получаем неравенство, не являющееся верным».
№ 877
а)
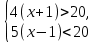
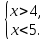
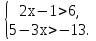
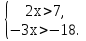
Ответ: решений нет
б)
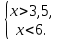
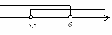
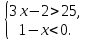
Ответ: x
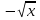 (-
(-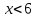 ; -1)
; -1) Пример2
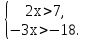
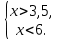
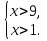
Ответ: x
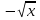 (9; +
(9; +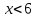 )
) Пример3
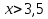
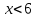
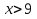
Ответ: решений нет.
№ 877
а)
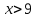
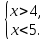
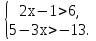
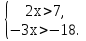 Ответ: решений нет
Ответ: решений нет б)
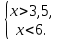

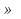
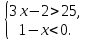 Ответ: x
Ответ: x 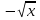 (-
(-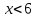 ; -1)
; -1) Задание на дом
А теперь запишем задание на дом: пункт 35, знать все определения, №880, №881. Все внимательно посмотрели на эти номера и прочитали задание. Нужно решить систему неравенств, делаем точно так же, как сегодня решали на уроке. У кого-то есть вопросы по домашнему заданию?
Вопросов нет.
П.35, №880, №881
Подведение итогов
Итак, сегодня на уроке мы с вами познакомились с понятием системы неравенств с одной переменной, дали определение решению системы неравенств с одной переменной и разъяснили, что значит решить систему. На этом наш урок окончен, спасибо за внимание, до свидания.
Домашнее задание.
№ 880 решите систему неравенств:
а) 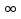
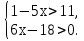
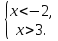
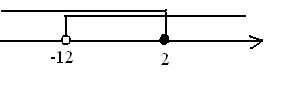
Ответ: x 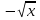 (-12; 2]
(-12; 2]
б) 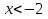
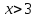
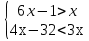
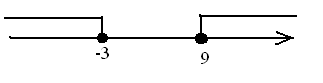
Ответ: решений нет.
в) 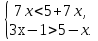
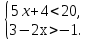
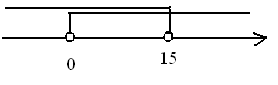
Ответ: x 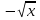 (0; 15)
(0; 15)
г)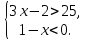
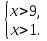
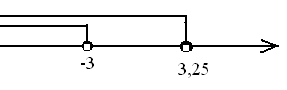
Ответ: : x 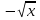 (-
(-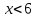 ; -3)
; -3)
№881 решите систему неравенств
а) 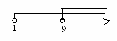
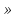
Ответ: x 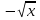 (-2; 0,8)
(-2; 0,8)
б) 
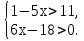
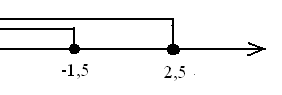 Ответ: x
Ответ: x 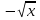 (-
(-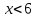 ;-1,5)
;-1,5)
в) 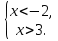
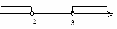
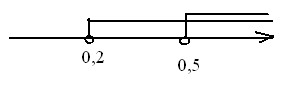
Ответ: x 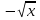 (0,5; +
(0,5; +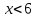 ).
).