Конспект урока Графики 9 класс

Учитель математики

МБОУ «Тыллыминская СОШ

имени С.З. Борисова»

Ксенофонтова Е.Н.

Тема урока: КАК ПОСТРОИТЬ ГРАФИК ФУНКЦИИ y = f( x + l ) + m, ЕСЛИ ИЗВЕСТЕН ГРАФИК ФНУКЦИИ y = f(x)

Цель: 1) в направлении личностного развития:

• развитие логического и критического мышления, куль­туры речи, способности к умственному эксперименту;

• формирование интеллектуальной честности и объектив­ности, способности к преодолению мыслительных стереоти­пов, вытекающих из обыденного опыта;

• воспитание качеств личности, обеспечивающих соци­альную мобильность, способность принимать самостоятель­ные решения;

• формирование качеств мышления, необходимых для адаптации в современном информационном обществе;

• развитие интереса к математическому творчеству и ма­тематических способностей;

2) в метапредметном направлении:

• развитие представлений о математике как форме опи­сания и методе познания действительности, создание условий для приобретения первоначального опыта математического моделирования;

• формирование общих способов интеллектуальной дея­тельности, характерных для математики и являющихся осно­вой познавательной культуры, значимой для различных сфер человеческой деятельности;

3) в предметном направлении:

• овладение математическими знаниями и умениями, не­обходимыми для продолжения образования, изучения смеж­ных дисциплин, применения в повседневной жизни;

• создание фундамента для математического развития, формирования механизмов мышления, характерных для мате­матической деятельности.

Характеристика основных видов деятельности

Вычислять значения функций, заданных формулами; со­ставлять таблицы значений функций.

Строить по точкам графики функций. Описывать свойства функции на основе ее графического представ­ления.

Моделировать реальные зависимости формулами и графиками. Читать графики реальных зависимостей.

Использовать функциональную символику для запи­си разнообразных фактов, связанных с рассматриваемы­ми функциями, обогащая опыт выполнения знаково-символических действий. Строить речевые конструкции с использованием функциональной терминологии.

Использовать компьютерные программы для по­строения графиков функций, для исследования положе­ния на координатной плоскости графиков функций в за­висимости от значений коэффициентов, входящих в формулу.

Распознавать виды изучаемых функций. Показывать схематически положение на координатной плоскости гра­фиков функций вида y = f( x); y = f( x + l ) + m в зависимости от значений коэффициентов, входящих в формулы.

Строить графики изучаемых функций; описывать их свойства

1. Организационный момент

«Математику, который привык быть экономичным в своих действиях, некоторые решение задач не очень нравятся, хотя оно абсолютно правильно. Математик спросит: зачем мне строить три графика, когда я могу обойтись построением только одного графика?»

2. Актуализация знаний

Вспомним функции , ,

Пример1: Построить график функции

Решение:y

-3

-2

-4

-5

-1

-6

-0

x

0

1

1

4

4

9

9

Пример2: Построить график функции

Решение:

3. Проблемное объяснение нового знания

Пример3: Постройте график функции

Решение: осуществим решение по этапам

Первый этап. Построим график функции (см.)

Второй этап. Сдвинув параболу на 2 единицы в право, получим график функции

(см.)

Третий этап. Сдвинув параболу на 3 единицы вниз, получим график функции

(см).</</u>

4. Первичное закрепление во внешней речи

Математик решит эту задачу так: Ведь фактически графиком функции является парабола, что служила графиком функции , только вершина параболы переместилась из начала координат в точку (2; -3). Поэтому продолжит математик, я сделаю так: перейдя к вспомогательной системе координат с началом (2; -3). Для этого постою (пунктиром) прямые и (см.). В этой вспомогательной системе координат воспользуюсь шаблоном параболы и получу в итоге требуемый график (см.).

5. Самостоятельная работа с самопроверкой

Пример4: Постройте график функции

Прмер5: Постройте график функции

Пример6: Постройте график функции

6. Включение нового знания в систему знаний и повторений

Алгоритм1:

1. Постройте график функции

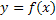
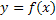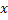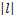2. Осуществить параллельный перенос графика вдоль оси на единиц масштаба влево, если 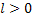, и вправо, если .

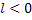3. Осуществить параллельный перенос полученного на втором шаге графика вдоль осу
   
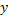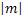   на единиц масштаба вверх, если 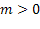, и вниз, если .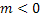

Алгоритм2:

1. Перейти к вспомогательной системе координат, проведя (пунктиром) вспомогательные прямые 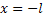, , 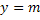т.е. выбрав начало новый системы координат точку .

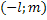2. К новой системе координат привязать график функции .

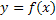Пример7: Постройте график функции .

7. Итог урока

1. Повторить алгоритмы

2. Домашнее задание.