Урок математики 'Сказочная карта' в 6 классе по теме 'Линейная функция'

Тандура О. Б.

Учитель математики 1 категории,

СОШ № 32, г. Уральск, ЗКО

Урок «Сказочная карта»

тема «Линейная функция», 6 класс, урок обобщения

Цели: способствовать формированию

- знаний - ученик должен знать:

- термины: график, абсцисса, ордината, координата, функция

- определение линейной функции, прямой пропорциональности

- умений - ученик должен уметь:

- определять, принадлежит ли точка графику

- задавать формулой линейную функцию, график которой параллелен, пересекает данную функцию

- определять положение графика на координатной плоскости

- определять взаимное расположение графиков двух линейных функций.

- Способствовать обучению школьников умению отвечать на вопросы учителя по изученному материалу.

- Способствовать формированию познавательного интереса к предмету,

логического мышления.

Содержание урока.

На доске карта сказочного леса.

1. Поляна «Теоретическая»

Играют несколько команд. На экране 16 вопросов. Каждая команда выбирает вопрос и отвечает: если правильно, то очки плюсуются, если неправильно, то вычитаются.

Вопросы:

1. Что такое функция?

2. Что называют графиком функции?

3. Как найти координаты точки пересечения двух прямых?

4. В каком случае графики двух линейных функций пересекаются?

5. Какую функцию называют линейной? (вопрос - аукцион)

6. Какую функцию называют прямой пропорциональностью?

7. В каком случае графики двух линейных функций являются параллельными прямыми?

8. В древности термина «функция» не было. Его ввел в 18 веке немецкий математик. Кто это?

9. В каком случае графики двух линейных функций пересекаются?

10. Что называют аргументом функции?

11. Груша тяжелее, чем яблоко, а яблоко тяжелее персика. Что тяжелее груша или персик?

12. Расшифруйте слова и назовите лишнее: д и р а у с, я у н ф к ц и, а т ч о к, я м а я п р

13. График некоторой линейной функции вида y=kx+1 параллелен графику функции y=-0,4x. Найдите значение k

14. Найдите закономерность и закончите числовой ряд: 0, 3, 8, 15, ? (кот в мешке)

15. График линейной функции - прямая, параллельная оси абсцисс и проходящая через точку M(5;8). Задайте эту функцию формулой

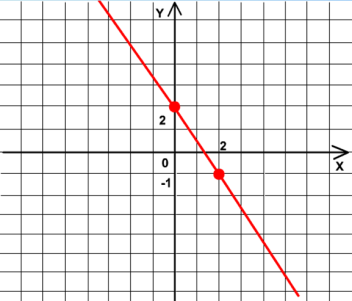
16. Каким уравнением задается эта функция?

2. Озеро «Графическое»

«Примеры учат больше, чем теория»

М.В. Ломоносов

На экране пять графиков.

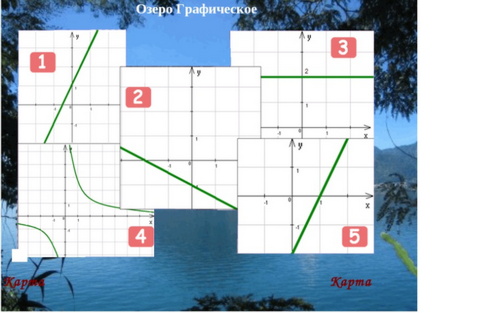
Вопросы:

1. На каком рисунке изображен график прямой пропорциональности?

2. У какой линейной функции угловой коэффициент отрицательный?

3. Найдите графики линейных функций с одинаковым угловым коэффициентом

4. Найдите график возрастающей линейной функции

5. Найдите график линейной функции

За правильный ответ - дополнительные баллы.

Ответы учащиеся дают с помощью сигнальных карточек .

3. Переправа знаний

На переправе организуется соревнование по рядам. Для этого нужно выполнить следующие задания (задания выполняются в тетради):

1. Дана функция y=-0,5x+1

Выясните, какие точки принадлежат графику этой функции.

2) При каком значении х значение функции равно 5

y=-0.5x+1 y=2x+1 y=4x+5

3) Постройте графики функции (три графика)

Проверку может осуществить соседний ряд.

4) Задайте формулой линейную функцию, график которой параллелен прямой y=-8x+11 и проходит через начало координат

4. Лес «Загадочный»

Выполнив тест, мы должны получить имя ученого, который ввел определение «функция»

1. Принадлежит ли точка А(4;2) графику функции, заданной формулой y=2x-6?

Э. Да В. Нет

2. Среди формул

а) y=12x-10

б) y=4-0,5x

в) y=15x

г) y=x(1-x)

д) y=x

укажите те, которые задают линейную функцию

К. в,г,д Л. б,г,д Й. а,б,в

3. Какой из графиков, представленных на рисунке, является графиком функции y=2x-6?

А. 1

В. 3

Л. 2

С. 4

4. При каком значении c график уравнения y=3x-c проходит через точку М(-3;1)?

К. -8 Е. -10 С. -6 М. среди ответов нет правильных

5. Какова формула линейной функции, график которой проходит через точку А (1;2), В (-1;-2)?

Р. y=2х

М. y=-2х

Д. y=-0,5х

К. среди ответов нет правильного

Код правильного ответа - ЭЙЛЕР.

Историческая справка

Окончательную формулировку определения функции с аналитической точки зрения сделал в 1748 году ученик Бернулли Эйлер: "Функция переменного количества есть аналитическое выражение, составленное каким-либо образом из этого количества и чисел или постоянных количеств". Так понимали функцию на протяжении почти всего 18 века

5. Опушка «Стихотворная»

Лучшее стихотворение, посвященное «Линейной функции»

Среди многих функций
Есть одна нужнейшая
Важная, старейшая.
Зовем ее линейная.(это слово закрыто, нужно отгадать)

Графиком которой
Является прямая,
Строгая, красивая,
Бесконечная такая.

Если k1 равно k2,
Прямые параллельные тогда.
А при этом b1 равно b2,
То прямые совпадут тогда.

При k1, не равном k2,
Прямые пересекаются всегда,
А при этом b1 равно b2,
Точка пересечения известна нам тогда.

И каков же тут итог,
Если наш учитель строг?
Любой ответ по «месту жительства» прямых
Найдем мы при условиях любых.

Можно организовать инсценирование этого стихотворения по четверостишиям, если позволяет время.

График учета настроения учащихся

На доске - графики линейной функции у=х; у=5; х=3. Каждый ученик приклеивает изображение настроения на график.