Пояснительная записка

Статус документа.

Рабочая программа учебного курса математики для 8-го класса составлена на основе:

федерального компонента государственного стандарта основного общего образования,

примерной программы по математике основного общего образования,

программ общеобразовательных учреждений (Алгебра. Ю.Н.Макарычев, Н.Г.Миндюк, К.И.Нешков, С.Б.Суворова.М. «Просвещение»2008г; Геометрия.Л.С.Атанасян, В.Ф.Бутузов, С.Б.Кадомцев. М., «Просвещение»,2009г.),

положения МБОУ «Подгорнобайларская ООШ» о рабочей программе учебного предмета, курса, дисциплины в образовательной организации общего образования, утвержденного приказом №168 от 23.08.2014 года.

Цели программы обучения математике в общеобразовательной школе определяются ее ролью в развитии общества в целом и формировании личности каждого отдельного человека. Математика нацелена на формирование математического аппарата для решения задач из математики и смежных предметов (физика, химия, основы информатики и вычислительной техники и др.), овладение системой математических знаний и умений, необходимых для применения практической деятельности изучения смежных дисциплин, продолжения образования; на достижение следующих целей:

• интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе: ясность и точность мысли, критичность мышления, интуиция, логическое мышление, элементы алгоритмической культуры, пространственных представлений;

• формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;

• воспитание культуры личности, отношения к математике как части общечеловеческой культуры, понимание значимости математики для научно технического прогресса;

• развитие представлений о полной картине мира, о взаимосвязи математики с другими предметами.

Задачи обучения математике:

• овладение системой математических знаний и умений, необходимых для применения практической деятельности изучения смежных дисциплин, продолжения образования;

• овладение навыками дедуктивных рассуждений;

• интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе: ясность и точность мысли, критичность мышления, интуиция, логическое мышление, элементы алгоритмической культуры, необходимой, в частности, для освоения курса информатики;

• формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;

• получение школьниками конкретных знаний о функциях как важнейшей математической модели для описания и исследования разнообразных процессов (равномерных, равноускоренных, экспоненциальных, периодических и т.д.);

• воспитание культуры личности, отношения к математике как части общечеловеческой культуры, понимание значимости математики для научно технического прогресса;

• развитие представлений о полной картине мира, о взаимосвязи математики с другими предметами.

Место учебного предмета. В соответствии с учебным планом на 2014/2015 учебный год на изучение курса математики в 8 классе на базовом уровне составляет 175 часов, по 5 часов в неделю.

Рабочая программа ориентирована на использование учебников: « Алгебра.8 кл. » Учебник для общеобразовательных учреждений, Ю.Макарычев,Н.Г.Миндюк,К.И.Нешков,С.Б.Суворова;под редакцией С.А.Теляковского.-15-е издание, доработанное.Москва.Просвещение,2008г, «Геометрия.7-9» Учебник для общеобразовательных учреждений, Л.С.Атанасян, В.Ф.Бутузов, С.Б.Кадомцев и др. -14-е издание. Москва. Просвещение. 2009.

Учебники включены в федеральный перечень учебников, утвержденный приказом МО и Н РФ от 31.03.2014 №253.

Характеристика предмета.

Математическое образование в основной школе складывается из следующих содержательных компонентов: арифметика; алгебра; геометрия; элементы комбинаторики, теории вероятностей, статистики и логики. В своей совокупности они отражают богатый опыт обучения математике в России, учитывают современные тенденции отечественной и зарубежной школы и позволяют реализовать поставленные перед школьным образованием цели на информационно емком и практически значимом материале. Эти содержательно значимые компоненты, развиваясь на протяжении всех лет обучения, естественным образом переплетаются и взаимодействуют в учебных курсах.

Содержание рабочей программы

Распределение учебного времени по математике

Наименование разделов и тем

8 класс

Арифметика

16

Натуральные числа

Дроби

Рациональные числа

Действительные числа

16

Текстовые задачи

Измерения, приближения, оценки

Алгебра

75

Алгебраические выражения

34

Уравнения и неравенства

41

Числовые последовательности

Числовые функции

Координаты

Геометрия

64

Начальные понятия и теоремы геометрии

Треугольник

20

Четырехугольник

18

Многоугольники

Окружность и круг

17

Измерение геометрических величин

7

Векторы

Геометрические преобразования

Построения с помощью циркуля и линейки

2

Элементы логики, комбинаторики, статистики и теории вероятностей.

7

Доказательства

Множества и комбинаторика

Статистические данные

4

Вероятность

3

Повторение

13

Итого

175

Рациональные дроби (23ч)

Рациональная дробь. Основное свойство дроби, сокращение дробей. Тождественные преобразования рациональных выражений. Функция у = к/х и ее график.

Понятия дробного выражения, рациональной дроби. Основное свойство дроби. Правило об изменении знака перед дробью. Правила сложения, вычитания дробей с одинаковыми и с разными знаменателями. Правила умножения, деления дробей, возведения дроби в степень. Понятие тождества, тождественно равных выражений, тождественных преобразований выражения. Рациональные выражения и их преобразования. Свойства и график функции

у = при k > 0; при k < 0.

Четырехугольники (14 ч).

Параллелограмм, его свойства и признаки. Прямоугольник, квадрат, ромб, их свойства и признаки. Трапеция, средняя линия трапеции; равнобедренная трапеция.

Квадратные корни (19 ч)

Понятие об иррациональных числах. Общие сведения о действительных числах. Квадратный корень. Понятие о нахождении приближенного значения квадратного корня. Свойства квадратных корней. Преобразования выражений, содержащих квадратные корни. Функция ее свойства и график.

Понятие рационального, иррационального, действительно числа, определение арифметического корня, теоремы о квадратном корне из произведения, из дроби, тождество = |x|.

Площадь (14 ч).

Площадь прямоугольника. Площадь параллелограмма, треугольника и трапеции (основные формулы

Теорема Пифагора. Признаки равенства прямоугольных треугольников. Синус, косинус, тангенс, котангенс острого угла прямоугольного треугольника и углов от 0° до 180°; приведение к острому углу. Решение прямоугольных треугольников.

Квадратные уравнения (20 ч)

Квадратное уравнение. Формула корней квадратного уравнения. Решение рациональных уравнений. Решение задач, приводящих к квадратным уравнениям и простейшим рациональным уравнениям.

Подобные треугольники (19 ч).

Признаки подобия треугольников.

Соотношения между сторонами и углами прямоугольного треугольника (5 ч). Основное тригонометрическое тождество. Формулы, связывающие синус, косинус, тангенс, котангенс одного и того же угла. Теорема косинусов и теорема синусов; примеры их применения для вычисления элементов треугольника.

Неравенства (20 ч)

Числовые неравенства и их свойства. Почленное сложение и умножение числовых неравенств. Погрешность и точность приближения. Линейные неравенства с одной переменной и их системы.

Окружность (17 ч).

Центр, радиус, диаметр. Дуга, хорда. Центральный, вписанный угол; величина вписанного угла. Взаимное расположение прямой и окружности, двух окружностей. Касательная и секущая к окружности; равенство касательных, проведенных из одной точки. Метрические соотношения в окружности: свойства секущих, касательных, хорд.

Окружность, вписанная в треугольник, и окружность, описанная около треугольника. Вписанные и описанные четырехугольники. Вписанные и описанные окружности правильного многоугольника.

Степень с целым показателем. Элементы статистики (10 ч.)

Степень с целым показателем и ее свойства. Стандартный вид числа. Приближенный вычисления.

Повторение (19 ч)

Требования к уровню подготовки учащихся.

В результате изучения курса математики 8-го класса учащиеся должны уметь:

• систематизировать сведения о рациональных и получить первоначальные представления об иррациональных числах;

• бегло и уверенно выполнять арифметические действия с рациональными числами; вычислять значения числовых выражений, содержащих степени и корни; научиться рационализировать вычисления;

• применять определение и свойства арифметических квадратных корней для вычисления значений числовых выражений и преобразования алгебраических выражений, содержащих квадратные корни;

• решать квадратные уравнения и уравнения, сводящиеся к ним, используя приемы и формулы для решения различных видов квадратных уравнений, графический способ решения уравнений; задачи, сводящиеся к решению квадратных уравнений;

• решать линейные неравенства с одной переменной, используя понятие числового промежутка и свойства числовых неравенств, системы линейных неравенств, задачи, сводящиеся к ним;

• понимать графическую интерпретацию решения уравнений и систем уравнений, неравенств;

• понимать содержательный смысл важнейших свойств функции; по графику функции отвечать на вопросы, касающиеся её свойств; строить графики функций - линейной, прямой и обратной пропорциональностей, квадратичной функции и функции ;

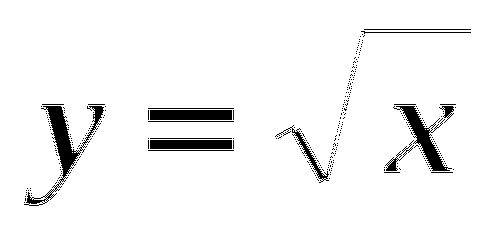• использовать приобретенные знания, умения, навыки в практической деятельности и повседневной жизни для:

• решения несложных практических расчетных задач, в том числе с использованием при необходимости справочной литературы, калькулятора, компьютера;

• устной прикидки, и оценки результата вычислений, проверки результата вычислений выполнением обратных действий;

• пользоваться геометрическим языком для описания предметов окружающего мира;

• распознавать геометрические фигуры, различать их взаимное расположение;

• изображать геометрические фигуры; выполнять чертежи по условию задач; осуществлять преобразование фигур;

• вычислять значения геометрических величин (длин, углов, площадей), в том числе: определять значение тригонометрических функций по заданным значениям углов; находить значения тригонометрических функций по значению одной из них; находить стороны, углы и площади треугольников, дуг окружности, площадей основных геометрических фигур и фигур, составленных из них;

• решать геометрические задания, опираясь на изученные свойства фигур и отношений между ними, применяя дополнительные построения, алгебраический и тригонометрический аппарат, соображения симметрии;

• проводить доказательные рассуждения при решении задач, используя известные теоремы, обнаруживая возможности для их использования.

Система оценивания

Для осуществления текущего контроля и промежуточной аттестации применяют следующие формы: контрольные работы, устные ответы, тесты (комплектация оценочно- методических работ прилагается).

Работы учащихся оцениваются в соответствии с положением об оценке качества общеобразовательной подготовки учащихся 5-9 классов МБОУ «Подгорнобайларская ООШ», утвержденным приказом №168 от 23.08.2014 года.

КРИТЕРИИ И НОРМЫ ОЦЕНКИ ЗНАНИЙ, УМЕНИЙ И НАВЫКОВ УЧАЩИХСЯ ПО МАТЕМАТИКЕ

1. Оценка письменных контрольных работ учащихся по математике.

Ответ оценивается отметкой «5», если:

• работа выполнена полностью;

• в логических рассуждениях и обосновании решения нет пробелов и ошибок;

• в решении нет математических ошибок (возможна одна неточность, описка,

которая не является следствием незнания или непонимания учебного

материала).

Отметка «4» ставится в следующих случаях:

• работа выполнена полностью, но обоснования шагов решения недостаточны

(если умение обосновывать рассуждения не являлось специальным объектом

проверки);

• допущены одна ошибка или есть два - три недочёта в выкладках, рисунках,

чертежах или графиках (если эти виды работ не являлись специальным

объектом проверки).

Отметка «3» ставится, если:

• допущено более одной ошибки или более двух - трех недочетов в выкладках,

чертежах или графиках, но обучающийся обладает обязательными умениями

по проверяемой теме.

Отметка «2» ставится, если:

• допущены существенные ошибки, показавшие, что обучающийся не обладает

обязательными умениями по данной теме в полной мере.

Отметка «1» ставится, если:

• работа показала полное отсутствие у обучающегося обязательных знаний и

умений по проверяемой теме или значительная часть работы выполнена не

самостоятельно.

Учитель может повысить отметку за оригинальный ответ на вопрос или оригинальное решение задачи, которые свидетельствуют о высоком математическом развитии обучающегося; за решение более сложной задачи или ответ на более сложный вопрос, предложенные обучающемуся дополнительно после выполнения им каких-либо других заданий.

2.Оценка устных ответов обучающихся по математике

Ответ оценивается отметкой «5», если ученик:

• полно раскрыл содержание материала в объеме, предусмотренном программой

и учебником;

• изложил материал грамотным языком, точно используя математическую

терминологию и символику, в определенной логической последовательности;

• правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;

• показал умение иллюстрировать теорию конкретными примерами, применять

ее в новой ситуации при выполнении практического задания;

• продемонстрировал знание теории ранее изученных сопутствующих тем,

сформированность и устойчивость используемых при ответе умений и

навыков;

• отвечал самостоятельно, без наводящих вопросов учителя;

• возможны одна - две неточности при освещение второстепенных вопросов

или в выкладках, которые ученик легко исправил после замечания учителя.

Ответ оценивается отметкой «4», если удовлетворяет в основном требованиям на оценку «5», но при этом имеет один из недостатков:

• в изложении допущены небольшие пробелы, не исказившее математическое

содержание ответа;

• допущены один - два недочета при освещении основного содержания ответа,

исправленные после замечания учителя;

• допущены ошибка или более двух недочетов при освещении второстепенных

вопросов или в выкладках, легко исправленные после замечания учителя.

Отметка «3» ставится в следующих случаях:

• неполно раскрыто содержание материала (содержание изложено

фрагментарно, не всегда последовательно), но показано общее понимание

вопроса и продемонстрированы умения, достаточные для усвоения

программного материала (определены «Требованиями к математической

подготовке обучающихся» в настоящей программе по математике);

• имелись затруднения или допущены ошибки в определении математической

терминологии, чертежах, выкладках, исправленные после нескольких

наводящих вопросов учителя;

• ученик не справился с применением теории в новой ситуации при выполнении

практического задания, но выполнил задания обязательного уровня сложности

по данной теме;

• при достаточном знании теоретического материала выявлена недостаточная

сформированность основных умений и навыков.

Отметка «2» ставится в следующих случаях:

• не раскрыто основное содержание учебного материала;

• обнаружено незнание учеником большей или наиболее важной части учебного

материала;

• допущены ошибки в определении понятий, при использовании математической

терминологии, в рисунках, чертежах или графиках, в выкладках, которые не

исправлены после нескольких наводящих вопросов учителя.

Отметка «1» ставится, если:

• ученик обнаружил полное незнание и непонимание изучаемого учебного

материала или не смог ответить ни на один из поставленных вопросов по

изученному материалу.

3.Оценка тестирования учащихся

«5»: 91-100% от общего числа баллов

«4»: 71-90% от общего числа баллов

«3»: 51-70% от общего числа баллов

«2»: 0-50% от общего числа баллов

Общая классификация ошибок.

При оценке знаний, умений и навыков обучающихся следует учитывать все ошибки (грубые и негрубые) и недочёты.

3.1. Грубыми считаются ошибки:

• незнание определения основных понятий, законов, правил, основных положений

теории, незнание формул, общепринятых символов обозначений величин, единиц

их измерения;

• незнание наименований единиц измерения;

• неумение выделить в ответе главное;

• неумение применять знания, алгоритмы для решения задач;

• неумение делать выводы и обобщения;

• неумение читать и строить графики;

• неумение пользоваться первоисточниками, учебником и справочниками;

• потеря корня или сохранение постороннего корня;

• отбрасывание без объяснений одного из них;

• равнозначные им ошибки;

• вычислительные ошибки, если они не являются опиской;

• логические ошибки.

3.2. К негрубым ошибкам следует отнести:

• неточность формулировок, определений, понятий, теорий, вызванная неполнотой

охвата основных признаков определяемого понятия или заменой одного - двух из

этих признаков второстепенными;

• неточность графика;

• нерациональный метод решения задачи или недостаточно продуманный план

ответа (нарушение логики, подмена отдельных основных вопросов

второстепенными);

• нерациональные методы работы со справочной и другой литературой;

• неумение решать задачи, выполнять задания в общем виде.

3.3. Недочетами являются:

• нерациональные приемы вычислений и преобразований;

• небрежное выполнение записей, чертежей, схем, графиков.

Перечень используемой оценочно-методической литературы

1. Дидактические материалы по алгебре для 8 класса. Ю.Н.Макарычев, Н.Г.Миндюк, К.И.Нешков, С.Б.Суворова. М: «Просвещение»,2007

2. Дидактические материалы по алгебре, Жохов В. И., Макарычкв Ю. Н., Миндюк Н. Г. 8 класс. - М.: Просвещение, 2007.

3. Разноуровневый контроль качества знаний по математике. 5-11 классы. М.П.Нечаев. М: «5за знания»,2006.

4. Промежуточная аттестация 7-8, Ф.Ф.Лысенко.М. Илекса, 2009.

5. Контрольные и проверочные по алгебре 7-9 классы. Звавич А. И., Шляпочкин Л. Я. М.: Просвещение, 2003.

6. Государственная итоговая аттестация. Математика. Типовые экзаменационные варианты под редакцией А.Л.Семенова,И.В.Ященко.30вариантов.Издательство «Национальное образование».Москва,2013.

7. Алгебра 7-8класс. Тесты для промежуточной аттестации. Под редакцией . Ф.Ф.Лысенко.Ростов-на-Дону. «Легион -М» 2010.

8. ГИА 3000задач с ответами.Математика. Три модуля: «Алгебра», «Геометрия», «Реальная математика». Под редакцией А.Л.Семеновой, И.В.Ященко. Москва, «Экзамен», 2014.

Учебно-методическое обеспечение

1. Алгебра.8 класс. Поурочные планы по учебнику Ю.Н.Макарычева, Н.Г.Миндюка, К.И.Нешкова, С.Б.Суворовой. Волгоград «Учитель»,2007.

2. Поурочные разработки по геометрии. 8 класс. Н.Ф.Гаврилова. М: «ВАКО»,2007.

3. Настольная книга учителя математики. М: ООО «Издательство АСТ», 2004.

4. Изучение геометрии в 7-9 классах. Атанасян Л.С. М. Просвещение 2003.

5. Учимся решать олимпиадные задачи. Геометрия. 5-11 классы. А.Ф.Фарков. М: «Айрис-пресс». 2006.

6. Подготовка к итоговой аттестации2013. Ф.Ф.Лысенко. Ростов- на- Дону. 2012.

Электронные ресурсы

Материально-техническое обеспечение

• Классная доска с набором приспособлений для крепления таблиц, картинок.

• Мультимейдийный проектор

• Ноутбук. Компьютер.

• Интерактивная доска

Календарно-тематическое планирование

по математике

Класс 8

Учитель Гимадиева Венера Камилевна

Количество часов

Всего 175 часов; в неделю 5 часов

Плановых контрольных уроков 15_, тестов ;

Административных контрольных уроков 2 ч.

Планирование составлено на основе Программы общеобразовательных учреждений под редакцией Т.А.Бурмистровой. Москва, «Просвещение», 2008г.

Учебник

« Алгебра.8 кл. » Учебник для общеобразовательных учреждений, Ю.Макарычев,Н.Г.Миндюк,К.И.Нешков,С.Б.Суворова;под редакцией С.А.Теляковского.-15-е издание, доработанное.Москва.Просвещение,2008г.

«Геометрия.7-9» Учебник для общеобразовательных учреждений, Л.С.Атанасян,В.Ф.Бутузов,С.Б.Кадомцев и др.-14-е издание.Москва.Просвещение.2009.

Дополнительная литература

1. Алгебра.8 класс.Поурочные планы по учебнику Ю.Н.Макарычева и др. Волгоград.Учитель,2007.

2.Дидактические материалы по алгебре для 8класса.Ю.Н.Макарычев,Н.Г.Миндюк и др. Москва.Просвещение.2007.

3.Поурочные разработки по геометрии.8класс.Н.Ф.Гаврилова.Москва.ВАКО,2007.

4.Самостоятельные и контрольные работы по алгебре и геометрии для 8 класса.А.П.Ершова и др.Москва.Илекса,2001.

5.Олимпиадные задания по математике.9-11классы.В.А.Шеховцев.Волгоград.Учитель,2007.

6.ГИА2009.Тематические тренировочные задания:9класс.Л.В.Кузнецова.Москва.Эксмо,2009.

7.Алгебра.9класс.Подготовка к итоговой аттестации 2012.Ф.Ф.Лысенко Ростов-на-Дону,2011.

8.Алгебра.Сборник заданий для подготовки к итоговой аттестации в 9классе. Л.В.Кузнецова. Москва.Просвещение,2008.

9.Разноуровневый контроль качества знаний по математике.5-11классы.М.П.Нечаев.Москва.

«5за знания».2006.

10.Настольная книга учителя математики.Москва.ООО «Издательство АСТ»,2004.

11.Алгебра 7-8класс. Тесты для промежуточной аттестации. Под редакцией . Ф.Ф.Лысенко.Ростов-на-Дону. «Легион -М» 2010.

12.ГИА 3000задач с ответами.Математика. Три модуля: «Алгебра», «Геометрия», «Реальная математика». Под редакцией А.Л.Семеновой, И.В.Ященко. Москва, «Экзамен», 2014.

13.Государственная итоговая аттестация. Математика. Типовые экзаменационные варианты под редакцией А.Л.Семенова,И.В.Ященко.30вариантов.Издательство «Национальное образование».Москва,2013.

Календарно-тематическое планирование

№

Тема урока и элементы содержания

Кол-во часов

Тип урока

Характеристика деятельности учащихся или виды учебной деятельности

Планируемые результаты освоения материала

Вид кон-троля, измерители

Дата проведения урока

план

факт

I

Блок 1. АЛГЕБРА. АЛГЕБРАИЧЕСКИЕ ВЫРАЖЕНИЯ.

Глава 1 .Рациональные дроби ( 23 ч.)

1

2

3

Рациональные выражения. Алгебраическая дробь. Рациональные выражения.

Допустимые значения переменных

Числовое значение буквенных выражений. Область определения.

1

1

1

КУ

УПЗУ

УОНМ

целые и дробные выражения, рациональные выражения, допустимые значения переменной

-уметь отличать целые и дробные выражения;

-уметь находить допустимые значения переменной

ФО [1], стр.4

ИРД

1.09

2.09.

3.09.

4

5

6

Основное свойство дроби. Сокращение дробей.

Тождественные преобразования выражений

1

1

1

КУ УПЗУ

УЗИМ

основное свойство дроби, сокращение дробей, тождественные преобразования, формулы сокращенного умножения (ФСУ)

-уметь применять ФСУ;

-уметь сокращать дроби после разложения на множители числителя и знаменателя

ФО

[1], стр.8

ПР [3], С-4 (1, 2)

4.09

5.09

8.09.

7

8

Действия с алгебраическими дробями. Сложение и вычитание дробей с одинаковыми знаменателями.

Упрощение выражений

1

1

УОНМ

КУ

сложение и вычитание дробей с одинаковыми знаменателями

-знать правило сложения и вычитания дробей с одинаковыми знаменателями;

-уметь пользоваться этим правилом при упрощении выражений

ФО [1], стр.16

ИРД

9.09

10.09

9

10

11

Сложение и вычитание дробей с разными знаменателями.

Преобразование в дробь выражений

Решение задач на повторение

1

1

1

УПЗУ

КУ

УЗИМ

сложение и вычитание дробей с разными знаменателями

-знать правило сложения и вычитания дробей с разными знаменателями;

-уметь пользоваться этим правилом при упрощении выражений

ФО [1], стр.19

ИРД

СР [3], С-7

11.09

12.09

15.09

12

Контрольная работа №1

«Сложение и вычитание дробей»

1

КЗУ

-уметь сокращать дроби после разложения на множители числителя и знаменателя;

-знать правило сложения и вычитания дробей с одинаковыми и разными знаменателями

[4], КР-1

16.09

13

14

Умножение дробей.

Возведение дроби в степень.

1

1

УОНМ

УЗИМ

числитель, знаменатель, сокращение дробей, ФСУ, правило умножения, возведение в степень

-знать правило умножения дробей;

-знать правило возведения в степень;

-уметь умножать дроби и возводить их в степень

ФО [1], стр.28

ИРД

17.09

18.09

15

16

Деление дробей.

Упрощение выражений

1

1

УОНМ

УПЗУ

правило деления дробей

-знать правило деления дробей;

-уметь делить дробь на дробь;

-уметь делить дробь на многочлен

ФО [1], стр.32

ИРД

СР [3],

С-9, 10

19.09

22.09

17

18

19

20

Рациональные выражения и их преобразования.

Упрощение выражений

Доказательство тождеств

Решение задач на повторение

1

1

1

1

УОНМ

УПЗУ

КУ

УЗИМ

рациональная дробь, сложение, вычитание, умножение, деление рациональных дробей

-уметь упрощать рациональные выражения, используя арифметические действия с рациональными дробями

ФО[1],

стр.36

СР [3], С-11

23.09

24.09

25.09

26.09

21

22

Функция и её график. Гипербола.

Построение графиков функций. График функции: модуль.

1

1

УОНМ

УПЗУ

обратно пропорциональные функции, график функции, гипербола

-уметь определять обратно пропорциональную функцию;

-уметь строить график функции;

-уметь определять знак числа k, зная расположение графика функции

ФО [1], стр.43

ИРД

29.09

30.09

23

Контрольная работа №2.

«Умножение и деление дробей.»

1

КЗУ

-уметь упрощать рациональные выражения, используя арифметические действия с рациональными дробями;

-уметь строить и работать с графиком функции

[4], КР-2

1.10

ГЕОМЕТРИЯ. ЧЕТЫРЕХУГОЛЬНИК.

Блок 2. Геометрия. Глава 5. Четырехугольники. ( 14 ч.)

24

Многоугольники. Длина ломаной, периметр многоугольника. Выпуклые многоугольники. Сумма углов выпуклого многоугольника.

1

УОНМ

1)Многоугольники.

2)Выпуклые многоугольники.

3) Сумма углов выпуклого многоугольника

Знать: определение многоугольника, формулу суммы углов выпуклого многоугольника.

Уметь: распознавать на чертежах многоугольники и выпуклые многоугольники, используя определение

УО

2.10

25

Решение задач.

Многоугольники

1

УПЗУ

1)Многоугольники.

2)Элементы многоугольника

Знать: формулу суммы углов многоугольника.

Уметь: применять формулу суммы углов выпуклого многоугольника при нахождении элементов многоугольника

СР№1

ДМ (15 мин)

3.10

26

Параллелограмм

1

УОНМ

Параллелограмм, его свойства

Знать: определение параллелограмма и его свойства.

Уметь: распознавать на чертежах среди четырехугольников

Индивидуальные карточки

6.10

27

Параллелограмм, его свойства и признаки.

1

КУ

Признаки параллелограмма

Знать: формулировки свойств и признаков параллелограмма. Уметь: доказывать,

ФО

7.10

28

Решение задач по теме «Параллелограмм»

1

УПЗУ

Параллелограмм, его свойства и признаки

Знать: определение, признаки и свойства параллелограмма. Уметь: выполнять чертежи по условию задачи, находить углы и стороны параллелограмма, используя свойства углов и сторон

СР№2

ДМ

(15 мин)

8.10

29

Трапеция. Равнобедренная трапеция.

1

КУ

1) Трапеция.

2) Средняя линия трапеции.

3) Равнобедренная трапеция, ее свойства

Знать: определение трапеции, свойства равнобедренной трапеции. Уметь: распознавать трапецию, ее элементы, виды на чертежах, находить углы и стороны равнобедренной трапеции, используя ее свойства

УО

9.10

30

Теорема Фалеса

1

УОНМ

Теорема Фалеса

Знать: формулировку теоремы Фалеса и основные этапы ее доказательства.

Уметь: применять теорему в процессе решения задач

Решение задач по готовым чертежам

10.10

31

Задачи на построение

1

КУ

Задачи на построение

Знать: основные типы задач на построение. Уметь: делить отрезок на п равных частей, выполнять необходимые построения

СР№4

ДМ (15 мин)

13.10

32

Прямоугольник

1

УОНМ

Прямоугольник, его элементы, свойства

Знать: определение прямоугольника, его элементы, свойства и признаки.

Уметь: распознавать на чертежах, находить стороны, используя свойства углов и диагоналей

УО

14.10

33

Ромб, квадрат

1

КУ

1) Понятие ромба, квадрата.

2) Свойства и признаки

Знать: определение ромба, квадрата как частных видов параллелограмма.

Уметь: распознавать и изображать ромб, квадрат, находить стороны и углы, используя свойства

Проверка домашнего задания

15.10

34

Осевая и центральная симметрия

1

КУ

Осевая и центральная симметрия как свойство геометрических фигур

Знать: виды симметрии в многоугольниках. Уметь: строить симметричные точки и распознавать фигуры, обладающие осевой и центральной симметрией

ФО

16.10

35

Решение задач.

Прямоугольник, квадрат, ромб, их свойства и признаки.

1

УПЗУ

1) Прямоугольник, ромб, квадрат.

2) Свойства признаки

Знать: определение, свойства и признаки прямоугольника, ромба, квадрата.

Уметь: выполнять чертеж по условию задачи, применять признаки при решении задач

СР№7

ДМ

(15 мин)

17.10

36

Решение задач. Осевая и центральная симметрия

1

УОСЗ

Четырехугольники: элементы,

Знать: формулировки определений, свойств и признаков

Теоретическая

20.10.

37

Контрольная работа № 3.

«Четырехугольники»

1

УКЗУ

Свойства и признаки прямоугольника, трапеции, ромба, параллелограмма

Уметь: находить в прямоугольнике угол между диагоналями, используя свойство диагоналей, углы в прямоугольной или равнобедренной трапеции, используя свойства трапеции

КР№3

ДМ (40 мин

21.10

Блок 3. Алгебра. Глава 2 . Квадратные корни (19 ч)

АРИФМЕТИКА. ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА.

38

Рациональные числа. Понятие об иррациональном числе. Иррациональность числа.

1

КУ

целые и дробные числа, рациональные числа

-четко знать определение рационального числа;

-уметь представлять рациональное число в виде бесконечной десятичной дроби;

-уметь сравнивать рациональные числа

ФО [1], стр.58

ИРД

22.10

39

Действительные числа как бесконечные десятичные дроби. Сравнение действительных чисел, арифметические действия над ними. Множество. Элемент множества, подмножество. Этапы развития представления о числе.

1

КУ

действительные числа, иррациональные числа

-уметь приводить примеры иррационального числа;

-уметь находить приближенное значение;

-знать, что множество действительных чисел состоит из рациональных и иррациональных чисел

ФО [1], стр.65

ИРД

23.10

40

41

Квадратный корень из числа Арифметический квадратный корень.

1

1

КУ УПЗУ

квадратный корень, арифметический квадратный корень, подкоренное выражение

-знать таблицу квадратов чисел от 1 до 25;

-уметь извлекать арифметический квадратный корень;

-знать в каком случае выражение имеет смысл;

-уметь выполнять преобразования с арифметическим квадратным корнем

ФО [1], стр.67

ИРК,

ИРД

МД [2],

Д-2.2

24.10

27.10

42

Уравнение .

1

УОНМ

корень уравнения, график функции

-знать когда уравнение не имеет корней, имеет один корень, имеет два корня;

-уметь строить график функции ;

-уметь решать уравнение графически

ФО [1], стр.71

ИРД

МД [2],

Д-2.2,

СР [3], С-15

28.10

43

Десятичные приближения иррациональных чисел. Нахождение приближенных значения корня с помощью калькулятора.

1

КУ

приближенные значения

-уметь находить приближенные значения арифметического квадратного корня с любой точностью

ФО [1], стр.74

ИРД,

29.10

44

График функции: корень квадратный. Функция и её график.

1

КУ

функция и её свойства, график функции

-уметь строить график функции ;

-уметь по графику находить значения x и y;

-уметь сравнивать числа, используя свойства функции

ФО [1], стр.78

ИРД

30.10

АЛГЕБРА. АЛГЕБРАИЧЕСКИЕ ВЫРАЖЕНИЯ.

45

Квадратный корень из произведения и дроби.

1

КУ

квадратный корень, корень из произведения, корень из дроби

-уметь пользоваться теоремой о корне из произведения и дроби;

-уметь находить значение выражений

ФО [1], стр.82

ИРД

31.10

46

47

Квадратный корень из степени.

Решение задач. Квадратный корень из степени

1

1

КУ

УПЗУ

квадратный корень, корень из степени, правило возведения степени в степень

-уметь пользоваться тождеством при нахождении значений выражений

ФО [1], стр.86

ИРД,

СР [3], С-18-20

10.11

11.11

48

Вынесение множителя из-под знака корня.

1

КУ

квадратный корень, вынесение множителя из-под знака корня

-уметь раскладывать подкоренное выражение на множители;

-уметь извлекать квадратный корень из числа -

ФО [1], стр.89

ИРД

12.11

49

50

Контрольная работа №4

«Квадратные корни.»

Сравнение значений выражений

1

1

КЗУ

УПЗУ

уметь представлять рациональное число в виде бесконечной десятичной дроби;

-уметь применять теоремы о квадратном корне из произведения, дроби и степени;

-уметь строить графики функций и

[4], КР-4

13.11

14.11

51

52

Внесение множителя под знак корня.

Решение задач на повторение

1

1

КУ

УПЗУ

квадратный корень, внесение множителя под знак корня

-уметь вносить множитель под знак корня

ФО [1], стр.90

СР [3], С-21

17.11

18.11

53

54

55

Свойства квадратных корней и их применение в вычислениях.

Сокращение дробей

Освобождение от иррациональности в знаменателе дроби

1

1

1

УОСЗ

КУ

КУ

корни из произведения, дроби и степени, умножение и деление корней, вынесение множителя из-под знака корня, внесение множителя под знак корня

-уметь применять все тождественные преобразования выражений, содержащих квадратные корни, в комплексе;

-уметь освобождаться от иррациональности в знаменателе

ФО [1], стр.93

СР [3], С-22

ИРД

19.11

20.11

21.11

56

Контрольная работа №5

«Преобразование выражений, содержащих квадратные корни.»

1

КЗУ

-уметь применять все тождественные преобразования выражений, содержащих квадратные корни, в комплексе

[4], КР-5

24.11

ГЕОМЕТРИЯ. ИЗМЕРЕНИЕ ГЕОМЕТРИЧЕСКИХ ФИГУР.

Блок 4. Геометрия. Глава 6 . Площадь (14 ч)

57

58

Анализ контрольной работы. Площадь многоугольника. Понятие о площади плоских фигур. Равносоставленные и равновеликие фигуры.

Площадь квадрата

1

1

УОНМ

УПЗУ

1) Понятие площади.

2) Равносоставленные и равно великие фигуры.

3)Свойства площадей

Знать: представление о способе измерения площади многоугольника, свойства площадей. Уметь: вычислять площадь квадрата

ФО

25.11

26.11

59

Площадь прямоугольника

1

КУ

Площадь прямоугольника

Знать: формулу площади прямоугольника. Уметь: находить площадь прямоугольника, используя формулу

Проверка дом. зад. Индив. карточки

27.11

60

Площадь параллелограмма

1

УОНМ

Площадь параллелограмма

Знать: формулу вычисления площади параллелограмма

УО

28.11

61

Площадь треугольника

1

КУ

Формула площади треугольника1) Площадь треугольника.

2) Теорема об отношении площадей треугольников, имеющих по равному углу

Знать: формулу площади треугольника. Уметь: доказывать теорему о площади треугольника, вычислять площадь треугольника, используя формулу

УО

1.12

62

Площадь трапеции

1

КУ

Теорема о площади трапеции

Знать: формулировку теоремы о площади трапеции и этапы ее доказательства. Уметь: находить площадь трапеции, используя формулу

УО

2.12

63

Решение задач .Площадь параллелограмма, треугольника и трапеции (основные формулы).

1

УОСЗ

Формулы площадей: прямоугольника, треугольника, параллелограмма, трапеции

Знать и уметь: применять формулы площадей при решении задач

Проверка задач самостоят, решения

3.12

64

Теорема Пифагора

1

УОНМ

Теорема Пифагора

Знать: формулировку теоремы Пифагора, основные этапы ее доказательства.

Уметь: находить стороны треугольника, используя теорему Пифагора

ФО

4.12

65

Теорема, обратная теореме Пифагора

1

КУ

Теорема, обратная теореме Пифагора

Знать: формулировку теоремы, обратной теореме Пифагора. Уметь: доказывать и применять при решении задач теорему, обратную теореме Пифагора

Индивидуальный опрос

5.12

66

Решение задач.

Площадь. Теорема Пифагора.

1

УПЗУ

Применение теоремы Пифагора и теоремы, обратной теореме Пифагора, при решении задач

Знать: формулировки теоремы Пифагора и ей обратной.

Уметь: выполнять чертеж по условию задачи, находить элементы треугольника, используя теорему Пифагора, определять вид треугольника, используя теорему, обратную теореме Пифагора

СР№13

ДМ (15 мин)

8.12

67

Повторение материала 1,2,3 блока

1

УОСЗ

уметь применять все тождественные преобразования выражений, содержащих квадратные корни, в комплексе

Текущий

9.12

68

Повторение материала 1,2,3 блока

1

УОСЗ

Индив. карточки

10.12

69

Контрольная работа №6

1

УКЗУ

1) Формулы вычисления площадей параллелограмма, трапеции

Уметь: находить площадь треугольника по известной стороне и высоте, проведенной к ней

КР№6

ДМ

(40 мин)

11.12

70

Контрольная работа №6

1

УКЗУ

1) Формулы вычисления площадей параллелограмма, трапеции

Уметь: находить площадь треугольника по известной стороне и высоте, проведенной к ней

КР№6

ДМ

(40 мин)

12.12

Блок 5. АЛГЕБРА. УРАВНЕНИЯ И НЕРАВЕНСТВА.

Глава 3 . Квадратные уравнения.( 20ч.)

71

72

Определение квадратного уравнения.

Неполные квадратные уравнения.

1

1

УОНМ

УЗИМ

квадратное уравнение, коэффициенты квадратного уравнения, неполное квадратное уравнение

-уметь распознавать квадратные уравнения по их виду;

-уметь решать неполные квадратные уравнения

ФО [1], стр.107

МД[2],Д-3.1

ИРД

15.12

16.12

73

Решение квадратных уравнений выделением квадрата двучлена.

1

КУ

квадратное уравнение, приведенное квадратное уравнение, выделение квадрата двучлена, ФСУ

-уметь выделять полный квадрат;

-уметь решать неполные квадратные уравнения

ФО [1], стр.111

ИРД

17.12

74

75

76

Квадратное уравнение: формула корней квадратного уравнения.

Нахождение корней уравнения по формуле 2.

Решение квадратных уравнений.

1

1

1

УПЗУ

УОНМ

УЗИМ

квадратное уравнение, формула дискриминанта квадратного уравнения, формула корней квадратного уравнения

-знать алгоритм нахождения корней квадратного уравнения;

-определять сколько корней имеет данное квадратное уравнение;

-уметь находить корни квадратного уравнения

ФО [1], стр.115

ИРД

СР [3], С-26

18.12

19.12

22.12

77

Решение задач с помощью квадратных уравнений.

1

КУ

квадратное уравнение, формула дискриминанта квадратного уравнения, формула корней квадратного уравнения, решение текстовых задач

-уметь составлять уравнение по условию задачи;

-уметь правильно решить квадратное уравнение по формуле

ФО [1], стр.119

ИРД

23.12

78

Теорема Виета. Соотношения между коэффициентами и корнями

1

УОНМ

приведенное квадратное уравнение, теорема Виета

-уметь с помощью теоремы Виета находить корни в простых квадратных уравнениях

ФО [1], стр.124

ИРД

24.12

79

Контрольная работа №7

«Квадратные уравнения» (директорская)

1

КЗУ

-уметь решать квадратное уравнение по формуле;

-уметь применять теорему Виета при нахождении корней в простых квадратных уравнениях;

-уметь решать задачи

[4], КР-7

25.12

80

Решение уравнений с параметрами

1

УПЗУ

МД[2] Д-3.2

26.12

81

82

83

84

Решение рациональных уравнений.

Нахождение корней уравнения

Решение уравнений

Решение уравнений

1

1

1

1

КУ

УОНМ

УОСЗ

УЗИМ

рациональное уравнение, целое и дробное рациональное уравнение, алгоритм решения дробных уравнений

-уметь распознавать рациональные уравнения по их виду;

-уметь решать дробные рациональные уравнения, используя алгоритм решения

ФО [1], стр.127

ИРД

СР [3], С-30

12.01

13.01

14.01

15.01

85

86

87

Решение текстовых задач с помощью рациональных уравнений.

Решение задач с помощью рациональных уравнений

Решение текстовых задач

1

1

1

КУ

УПЗУ

УЗИМ

рациональное уравнение, решение задач

-уметь решать текстовые задачи с использованием рациональных уравнений

ФО [1], стр.130

ИРД

МД[2] Д-4.1

16.01

19.01

20.01

88

89

Графический способ решения уравнений.

Графический способ решения уравнений

1

1

УОСЗ

УПЗУ

график функции, графический способ решения уравнений

-уметь строить графики функций;

-уметь по графику определять корни уравнения

ФО [1], стр.133

21.01

22.01

90

Контрольная работа №8

«Рациональные уравнения»

1

КЗУ

-уметь использовать алгоритм при решении дробных уравнений;

-уметь решать задачи;

-уметь графически решать уравнения

[4], КР-8

23.01

ГЕОМЕТРИЯ. ТРЕУГОЛЬНИК

Блок 6. Геометрия. Глава 7. Подобные треугольники.( 19ч.)

91

Анализ контрольной работы. Подобие треугольников. Коэффициент подобия.

1

УОНМ

1) Подобие треугольников.

2) Коэффициент подобия

Знать: определение пропорциональных отрезков подобных треугольников, свойство биссектрисы треугольника.

Уметь: находить элементы треугольника, используя свойство биссектрисы о делении противоположной стороны

УО

26.01

92

Связь между площадями подобных фигур.

1

КУ

Связь между площадями подобных фигур

Знать: формулировку теоремы об отношении площадей подобных треугольников. Уметь: находить отношения площадей, составлять уравнения, исходя из условия задачи

СР№16

ДМ (15 мин)

27.01

93

Первый признак подобия треугольников

1

УОНМ

Первый признак подобия треугольников

Знать: формулировку первого признака подобия треугольников, основные этапы его доказательства.

Уметь: доказывать и применять при решении задач первый признак подобия треугольников, выполнять чертеж по условию задачи

ФО

28.01

94

Второй признак подобия треугольников

1

УЗИМ

Второй признак подобия треугольников

Знать: формулировку второго признака подобия треугольников, основные этапы его доказательства.

Уметь: доказывать и применять при решении задач второго признака подобия треугольников, выполнять чертеж по условию задачи

УО

29.01

95

Третий признак подобия треугольников

1

УОНМ

Второй и третий признаки подобия треугольников

Знать: формулировки второго и третьего признаков подобия треугольников. Уметь: проводить доказательства признаков, применять их при решении задач

Знать: формулировки второго и третьего признака

30.01

96

Решение задач по теме: «Признаки подобия треугольников»

1

УОСЗ

Применение признаков подобия при решении задач

Уметь: доказывать подобия треугольников и находить элементы треугольника, используя признаки подобия

Проверка задач самостоят, решения

2.02

97

Контрольная работа № 9

«Признаки подобия треугольников»

1

УКЗУ

Признаки подобия треугольников

Уметь: находить стороны, углы, отношения сторон, отношение периметров и площадей подобных треугольников, используя признаки подобия. Доказывать подобия треугольников, используя наиболее эффективные признаки подобия

КР№9

ДМ

(40 мин)

3.02

98

Анализ контрольной работы. Средняя линия треугольника

1

УОНМ

Средняя линия треугольника

Знать: формулировку теоремы о средней линии треугольника. Уметь: проводить доказательство теоремы о средней линии треугольника, находить среднюю линию треугольника

УО

4.02

99

Свойство медиан треугольника

1

КУ

Свойство медиан треугольника

Знать: формулировку свойства медиан треугольника

Уметь: находить элементы треугольника, используя свойство медианы

СР № 19

ДМ (15 мин)

5.02

100

Пропорциональные отрезки

1

КУ

Среднее пропорциональное

Знать: понятие среднего пропорционального, свойство высоты прямоугольного треугольника, проведенной из вершины прямого угла.

Уметь: находить элементы прямоугольного треугольника, используя свойство высоты

Индивидуальные карточки

6.02

101

Пропорциональные отрезки в прямоугольном треугольнике

1

УПЗУ

Пропорциональные отрезки в прямоугольном треугольнике

Знать: теоремы о пропорциональности отрезков в прямоугольном треугольнике. Уметь: использовать теоремы при решении задач

ФО

9.02

102

Измерительные работы на местности

1

УПЗУ

Применение подобия треугольников в измерительных работах на местности

Знать: как находить расстояние до недоступной точки. Уметь: использовать подобие треугольников в измерительных работах на местности, описывать реальные ситуации на языке геометрии

СР № 20

ДМ (15 мин)

10.02

103

Задачи на построение

1

УОСЗ

Задачи на построение

Знать: этапы построений.

Уметь: строить биссектрису, высоту, медиану треугольника; угол, равный данному; прямую, параллельную данной

УО

11.02

104

Задачи на построение методом подобных треугольников

1

УПЗУ

Метод подобия

Знать: метод подобия.

Уметь: применять метод подобия при решении задач на построение

Текущий

12.02

105

Синус, косинус, тангенс, котангенс острого угла прямоугольного треугольника и углов от 0° до 180°; приведение к острому углу.

1

УОНМ

1)Понятие синуса, косинуса, тангенса острого угла прямоугольного треугольника. 2) Основное тригонометрическое тождество

Знать: понятие синуса, косинуса, тангенса острого угла прямоугольного треугольника. Основное тригонометрическое тождество. Уметь: находить значения одной из тригонометрических функций по значению другой

ФО

13.02

106

Значения синуса, косинуса, тангенса для углов 30°, 45°, 60°, 90°

1

КУ

Синус, косинус и тангенс углов 30°, 45°, 60°, 90°

Знать: значения синуса, косинуса и тангенса для углов 30°, 45°, 60°, 90°.

Уметь: определять значения синуса, косинуса, тангенса по заданному значению углов

УО

16.02

107

Решение прямоугольных треугольников

1

УОНМ

Решение прямоугольных треугольников

Знать: соотношения между сторонами и углами прямоугольного треугольника. Уметь: решать прямоугольные треугольники, используя определение синуса, косинуса, тангенса острого угла

Проверка домашнего задания

СР № 23 ДМ

(15 мин)

17.02

108

Решение задач. Соотношения между сторонами и углами прямоугольного треугольника

1

УОСЗ

Задачи на применение теории подобия треугольников и соотношений между сторонами

Знать и уметь: применять теорию подобия треугольников, соотношения между сторонами и углами прямоугольного треугольника при решении задач.

Уметь: выполнять чертеж по условию задачи, решать геометрические задачи с использованием тригонометрии

Проверка задач самостоят, решения

18.02

109

Контрольная работа

№ 10 по теме: «Применение подобия треугольников, соотношения между сторонами и углами прямоугольного треугольника»

1

УПЗУ

Средняя линия треугольника. Свойство медиан треугольника. Соотношения между сторонами и углами прямоугольного треугольника

Уметь: находить стороны треугольника по отношению средних линий и периметру. Решать прямоугольный треугольник, используя соотношения между сторонами и углами. Находить стороны треугольника, используя свойство точки пересечения медиан

КР№10

ДМ (40 мин)

19.02

Блок 7. АЛГЕБРА. УРАВНЕНИЯ И НЕРАВЕНСТВА.

Глава 4 . Неравенства.( 20ч.)

110

111

112

Числовые неравенства.

Числовые неравенства и их свойства.

Доказательство числовых и алгебраических неравенств.

1

1

1

КУ УПЗУ

УОНМ

числовые неравенства, свойства числовых неравенств

-уметь доказывать неравенства, используя определение числового неравенства;

-знать все свойства и применять их к оценке значения выражений

ФО [1], стр.149

ИРД

СР [3], С-34

20.02

24.02

25.02

113

114

115

116

117

Оценивание значений выражений

Сложение числовых неравенств.

Умножение числовых неравенств.

Оценивание значений выражений

Урок обобщения и систематизации знаний по теме " Числовые неравенства"

1

1

1

1

1

КУ

УПЗУ

УПЗУ

УПЗУ

УПЗУ

числовые неравенства, свойства числовых неравенств, теоремы о почленном сложении и умножении числовых неравенств

-уметь почленно складывать неравенства;

-уметь почленно умножать неравенства;

-уметь оценивать сумму, разность, произведение

ФО[1],

стр. 152

ИРД

ИРК

26.02

27.02

2.03

3.03

4.03

118

Контрольная работа №11

«Числовые неравенства»

1

КЗУ

-уметь почленно складывать и умножать неравенства;

-уметь применять свойства к оценке значения выражений

[4], КР-11

5.03

119

120

Множество. Пересечение и объединение множеств. Числовые промежутки: интервал, отрезок, луч.

Работа с числовыми промежутками

1

1

УОНМ

УПЗУ

числовой промежуток, изображение на координатной прямой

-уметь изображать числовые промежутки на координатной прямой, удовлетворяющих неравенству;

-уметь изображать пересечение и объединение множеств

ФО [1], стр.156

ИРД

6.03

10.03

121

122

123

124

Неравенство с одной переменной. Решение неравенства.

Решение упражнений по теме" Неравенства с одной переменной"

Решение задач по теме "Неравенства с одной переменной"

Решение задач по теме "Неравенства с одной переменной"

1

1

1

1

УОНМ

УОСЗ

УПЗУ

УПЗУ

линейные неравенства с одной переменной, равносильные неравенства, числовой промежуток, свойства неравенств

-уметь решать неравенства с одной переменной;

-уметь изображать множество решений неравенства на числовой прямой;

-уметь решать простейшие неравенства вида , , при ;

-знать в каком случае неравенства либо не имеют решений, либо их решением является любое число

ФО [1], стр.161

ИРД,

ИРК

МД [2], стр.73, Д-1.1

ПР[3], С-40

11.03

12.03

13.03

16.03

125

126

127

128

Линейные неравенства с одной переменной и их системы.

Решение упражнений по теме " Системы неравенств"

Решение двойных неравенств

Контрольная работа №12

"Неравенства с одной переменной"

1

1

1

1

КУ

УПЗУ

УОНМ

КЗУ

система линейных неравенств с одной переменной, числовой промежуток

-знать, что значит «решить систему»;

-уметь решать систему линейных неравенств с одной переменной;

-уметь изображать множество решений системы на числовой прямой

ФО [1], стр.168

ИРД

СР [3], С-41

[4],

КР-12

17.03

18.03

19.03

20.03

129

Решение систем нескольких неравенств.

1

УЗИМ

-уметь решать неравенства с одной переменной и изображать множество решений неравенства на числовой прямой;

-уметь решать систему линейных неравенств с одной переменной и изображать множество решений системы на числовой прямой

1.04

ГЕОМЕТРИЯ. ОКРУЖНОСТЬ И КРУГ.

Блок 8. Геометрия. Глава 8 . Окружность ( 17ч.)

130

Анализ контрольной работы. Взаимное расположение прямой и окружности, двух окружностей.

1

УОНМ

Взаимное расположение прямой и окружности

Знать: случаи взаимного расположения прямой и окружности. Уметь: определять взаимное расположение прямой и окружности, выполнять чертеж по условию задачи

ФО

2.04

131

Касательная и секущая к окружности. Равенство касательных, проведенных из одной точки.

1

КУ

1) Касательная секущая к окружности.

2) Точка касания

Знать: понятие касательной, точек касания, свойство касательной и ее признак. Уметь: доказывать теорему о свойстве касательной и ей обратную, проводить касательную к окружности

Теоретический

опрос

3.04

132

Решение задач

1

УПЗУ

1) Касательная и секущая к окружности.

2) Равенство отрезков касательных, проведенных из одной точки.

3) Свойство касательной и ее признак

Знать: взаимное расположение прямой и окружности; формулировку свойства касательной о ее перпендикулярности радиусу; формулировку свойства отрезков касательных, проведенных из одной точки.

Уметь: находить радиус окружности, проведенной в точку касания, по касательной и наоборот

СР № 25

ДМ (15 мин)

6.04

133

Центральный угол. Градусная мера угла, соответствие между величиной угла и длиной дуги окружности.

1

УОНМ

Центральные и вписанные углы.

Градусная мера дуги окружности

Знать: понятие градусной меры дуги окружности, понятие центрального угла. Уметь: решать простейшие задачи на вычисление градусной меры дуги окружности

УО

7.04

134

Центральный, вписанный угол. Величина вписанного угла. Теорема о вписанном угле

1

УОНМ

1) Понятие вписанного угла.

2) Теорема о вписанном угле и следствия из нее

Знать: определение вписанного угла, теорему о вписанном угле и следствия из нее. Уметь: распознавать на чертежах вписанные углы, находить величину вписанного угла

Проверка домашнего задания

8.04

135

Теорема об отрезках пересекающихся хорд

1

КУ

Теорема об отрезках пересекающихся хорд

Знать: формулировку теоремы, уметь доказывать и применять ее при решении задач, выполнять чертеж по условию задачи

Текущий

9.04

136

Метрические соотношения в окружности: свойства секущих, касательных, хорд.

1

КУ

Центральные и вписанные углы

Знать: формулировки определений вписанного и центрального углов, теоремы об отрезках пересекающихся хорд.

Уметь: находить величину центрального и вписанного угла

СР № 27

ДМ (15 мин)

10.04

137

Свойство биссектрисы угла

1

УОНМ

Теорема о свойстве биссектрисы

угла

Знать: формулировку теоремы о свойстве равноудаленности каждой точки биссектрисы угла и этапы ее доказательства.

Уметь: находить элементы треугольника, используя свойство биссектрисы; выполнять чертеж по условию задачи

ФО

13.04

138

Свойство серединного перпендикуляра к отрезку

1

КУ

1) Понятие серединного перпендикуляра.

2) Теорема

о серединном перпендикуляре

Знать: понятие серединного перпендикуляра, формулировку теоремы о серединном перпендикуляре. Уметь: доказывать и применять теорему для решения задач на нахождение элементов треугольника

Теоретический опрос

14.04

139

Теорема о точке пересечения высот треугольника

1

КУ

1) Теорема

о точке пересечения высот треугольника.

2) Четыре замечательные точки треугольника

Знать: четыре замечательные точки треугольника, формулировку теоремы о пересечении высот треугольника. Уметь: находить элементы треугольника

СР № 29

ДМ (15 мин)

15.04

140

Вписанная окружность

1

УОНМ

1) Понятие вписанной окружности.

2) Теорема об окружности, вписанной в треугольник

Знать: понятие вписанной окружности, теорему об окружности, вписанной в треугольник. Уметь: распознавать на чертежах вписанные окружности, находить элементы треугольника, используя свойства вписанной окружности

Индивидуальный теоретический опрос

16.04

141

Свойство описанного четырехугольника.

1

КУ

Теорема о свойстве описанного четырехугольника

Знать: теорему о свойстве описанного четырехугольника и этапы ее доказательства. Уметь: применять свойство описанного четырехугольника при решении задач, выполнять чертеж по условию задачи

Проверка домашнего задания. УО

17.04

142

Описанная окружность. Окружность, вписанная в треугольник, и окружность, описанная около треугольника.

1

УОНМ

1) Описанная окружность.

2) Теорема об окружности, описанной около треугольника

Знать: определение описанной окружности, формулировку теоремы об окружности, описанной около треугольника. Уметь: проводить доказательство теоремы и применять ее при решении задач, различать на чертежах описанные окружности

УО

20.04

143

Свойство вписанного четырехугольника. Вписанные и описанные четырехугольники.

1

КУ

Свойство углов вписанного четырехугольника

Знать: формулировку теоремы о вписанном четырехугольнике. Уметь: выполнять чертеж по условию задачи, решать задачи, опираясь на указанное свойство

МД№4

ДМ (20 мин)

21.04

144

Замечательные точки треугольника: точки пересечения серединных перпендикуляров, биссектрис, медиан». Окружность Эйлера.

1

УОСЗ

1) Вписанная и описанная окружности.

Знать: формулировки определений и свойств. Уметь: решать простейшие геометрические задачи, опираясь на изученные свойства

Проверка домашнего задания, задач для самостоятельного решения

22.04

145

Решение задач по теме «Окружность»

1

КУ

2) Вписанные и описанные четырехугольники

Знать: формулировки определений и свойств. Уметь: решать простейшие геометрические задачи, опираясь на изученные свойства

домашнего задания, задач для самостоятельного решения

23.04

146

Контрольная работа № 13

«Окружность»

1

УКЗУ

Контроль и оценка знаний и умений

Уметь: находить один из отрезков касательных, проведенных из одной точки по заданному радиусу окружности; находить центральные и вписанные углы по отношению дуг окружности; находить отрезки пересекающихся хорд окружности, используя теорему о произведении отрезков пересекающихся хорд

КР№13

ДМ (40 мин)

24.04

Блок 9. Алгебра. Глава 5 . Степень с целым показателем. Элементы статистики. (10 ч.)

АРИФМЕТИКА

РАЦИОНАЛЬНЫЕ ЧИСЛА

147

Степень с целым показателем. Определение.

1

КУ

степень с целым показателем, степень с отрицательным показателем

-знать, как записывают число в виде степени с отрицательным показателем;

-уметь выполнять действия над степенями с целыми показателями

ФО [1], стр.180

ИРД

27.04

148

Свойства степени с целым показателем.

1

КУ

степень с целым показателем, свойства степени с целым показателем

-уметь применять свойства степени с целым показателем при вычислениях, нахождении значений выражений и упрощении выражений;

-знать, что при делении степеней с одинаковыми основаниями, показатели степеней делимого и делителя могут быть любыми целыми числами

ФО [1], стр.183

ИРД

ПР [3], С-44

28.04

149

Стандартный вид числа. Выделение множителя-степени десяти в записи числа.

1

КУ

стандартный вид числа

-уметь представлять число в виде , где и n - целое число

ФО [1], стр.188

ИРД

29.04

150

Запись приближенных значений.

1

КУ

абсолютная и относительная погрешность, верные цифры

-уметь выполнять действия с приближенными значениями;

-уметь оценивать абсолютную погрешность приближенного значения в случае, если все цифры верные

ФО [1], стр.192

ИРД

30.04

151

Действия над приближенными значениями.

1

КУ

округление чисел

-уметь округлять при сложении, вычитании, умножении и делении приближенных значений, в записи которых все цифры верные

ФО [1], стр.194

ИРД

4.05

152

Вычисления с приближенными данными на калькуляторе.

1

КУ

вычисления с приближенными данными на калькуляторе.

-уметь выполнять действия с приближенными значениями на калькуляторе

ФО [1], стр.199

5.05

ЭЛЕМЕНТЫ СТАТИСТИКИ. СТАТИСТИЧЕСКИЕ ДАННЫЕ.

153

Представление данных в виде таблиц, диаграмм, графиков

1

УОНМ

элементы статистики, относительные частоты

уметь проводить наблюдения и результаты заносить в итоговые таблицы

ФО

6.05

154

155

Средние результаты измерений. Мода, медиана, размах

Наглядное представление статистической информации

1

1

КУ

УПЗУ

элементы статистики, относительные частоты

-уметь проводить наблюдения и результаты заносить в итоговые таблицы

ФО

7.05

8.05

156

Представление данных в виде таблиц, диаграмм, графиков

.

1

КУ

элементы статистики, относительные частоты, столбчатая диаграмма, полигон частот

-уметь систематизировать полученные данные и графически представлять результаты наблюдений

ФО

МД

11.05

Блок 10. Повторение курса математики 8 класса. (19ч.)

157

Четырехугольники

1

УОСЗ

Четырехугольники: определения, свойства; 2) признаки, площадь

Знать: формулировки определений, свойств, признаков: параллелограмма, ромба, трапеции. Уметь: находить элементы четырехугольников, опираясь на изученные свойства, выполнять чертеж по условию задачи; вычислять площадь четырехугольника

УО

12.05

158

Площадь многоугольника

1

УОНМ

1) Понятие площади.

2) Равносоставленные и равно великие фигуры.

3)Свойства площадей

Знать: представление о способе измерения площади многоугольника, свойства площадей. Уметь: вычислять площадь квадрата

ФО

13.05

159

Решение задач по теме: «Признаки подобия треугольников»

1

УОСЗ

Применение признаков подобия при решении задач

Уметь: доказывать подобия треугольников и находить элементы треугольника, используя признаки подобия

Проверка задач самостоят, решения

14.05

160

Касательная к окружности

1

УПЗУ

1) Касательная и секущая к окружности.

2) Равенство отрезков касательных, проведенных из одной точки.

3) Свойство касательной и ее признак

Знать: взаимное расположение прямой и окружности; формулировку свойства касательной о ее перпендикулярности радиусу; формулировку свойства отрезков касательных, проведенных из одной точки.

Уметь: находить радиус окружности, проведенной в точку касания, по касательной и наоборот

СР № 25

ДМ (15 мин)

15.05

161

Преобразование рациональных выражений.

1

КУ

обыкновенные дроби, числитель, знаменатель, общий знаменатель

-уметь приводить дроби к общему знаменателю;

-уметь выполнять арифметические действия с дробями с разными знаменателями

ФО

ИРД

18.05

162

Применение свойств арифметического квадратного корня.

1

КУ

УПЗУ

вынесение множителя из-под знака корня, внесение множителя под знак корня

-уметь выполнять преобразование выражений, содержащих квадратные корни в комплексе

ФО

ИРД

19.05

163

Промежуточная аттестация. Тестирование.

1

КЗУ

Знать: формулировки определений, свойств. Уметь: решать задачи, опираясь на изученное

Т

20.05

164

Формула корней квадратного уравнения.

1

КУ

квадратное уравнение, формула дискриминанта, формула корней квадратного уравнения

-уметь решать квадратные уравнения по формуле

ФО

ИРД

21.05

165

Неравенства с одной переменной и их системы.

1

КУ

числовые промежутки, неравенства с одной переменной, системы неравенств с одной переменной

-уметь решать простейшие неравенства вида , , при ;

-уметь изображать множество решений неравенства на числовой прямой;

-уметь решать систему линейных неравенств с одной переменной и изображать множество решений системы на числовой прямой

ФО

ИРД

22.05

166

Степень с целым показателем.

1

КУ

степень с целым показателем и её свойства, стандартный вид числа

-уметь выполнять действия над степенями с целыми показателями;

-уметь записывать числа в стандартном виде

ФО

ИРД

25.05

167

Окружность. Повторение

1

УОСЗ

1) Вписанная и описанная окружности.

Знать: формулировки определений и свойств. Уметь: решать простейшие геометрические задачи, опираясь на изученные свойства

ИРД

25.05

168

Касательная к окружности

1

УПЗУ

2) Вписанные и описанные четырехугольники

Знать: формулировки определений и свойств. Уметь: решать простейшие геометрические задачи, опираясь на изученные свойства

СР

26.05

169

Контрольная работа №14

«Степени с целым показателем.»

1

КЗУ

-уметь выполнять действия над степенями с целыми показателями;

-уметь записывать числа в стандартном виде;

-уметь находить приближенное значение суммы, разности, произведения и частного

[4], КР-14

26.05

170

Повторение. Подобие треугольников

1

УОСЗ

Ф

27.05

171

Повторение.

Преобразование выражений

1

КУ

Преобразование рациональных выражений

-уметь находить значение рациональных выражений, владея навыком выполнения арифметических действий с рациональными дробями;

ИРД

27.05

172

Повторение. Уравнения и неравенства

1

УОСЗ

-уметь решать квадратные уравнения, неравенства, системы неравенств и все виды текстовых задач, изученных в 8 классе

Ф

28.05

173

Повторение. Квадратные уравнения

1

УОСЗ

рациональные дроби, квадратные корни и уравнения, неравенства и их системы, степень с целым показателем

-уметь решать квадратные уравнения, неравенства, системы неравенств и все виды текстовых задач, изученных в 8 классе

Ф

28.05

174

Решение заданий ГИА

1

УОСЗ

Ф

29.05

175

Решение заданий ГИА

1

УОСЗ

Ф

29.05

Сокращения, используемые в рабочей программе:

Типы уроков:

УОНМ - урок ознакомления с новым материалом.

УЗИМ - урок закрепления изученного материала.

УПЗУ - урок применения знаний и умений.

УОСЗ - урок обобщения и систематизации знаний.

УПКЗУ - урок проверки и коррекции знаний и умений.

КЗУ- контроль знаний и умений

КУ - комбинированный урок.

Виды контроля:

ФО - фронтальный опрос.

ИРД - индивидуальная работа у доски.

ИРК - индивидуальная работа по карточкам.

СР - самостоятельная работа.

ПР - проверочная работа.

МД - математический диктант.

Т - тестовая работа.

Приложение к рабочей программе

Комплект оценочных и методических материалов

по математике для 8 класса

на 2014/2015 учебный год

АЛГЕБРА

Контрольная работа № 1.

1 вариант

1). Сократить дробь:

2). Представьте в виде дроби:

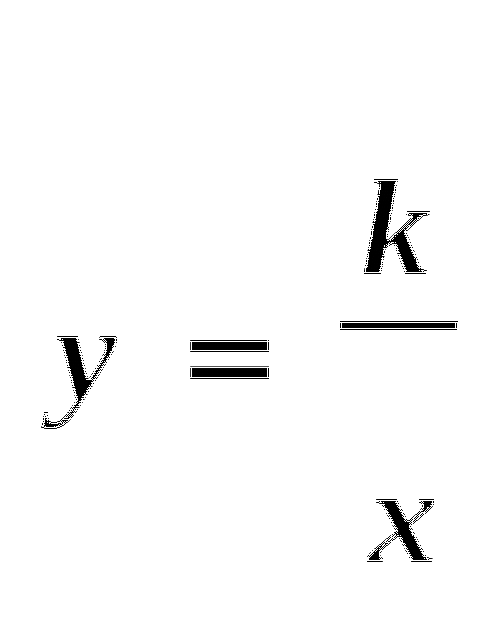
3). Найдите значение выражения

при а = 0,2, в = - 5.

4). Упростите выражение:

2 вариант

1). Сократить дробь:

2). Представьте в виде дроби:

3). Найдите значение выражения

при х = - 8, у = 0,1.

4). Упростите выражение:

Контрольная работа № 2.

1 вариант

1). Представьте в виде дроби:

2). Постройте график функции .

Какова область определения функции? При каких значениях х функция принимает отрицательные значения?

3). Докажите, что при всех значениях в ≠ ± 1 значение выражения

не зависит от в.

2 вариант

1). Представьте в виде дроби:

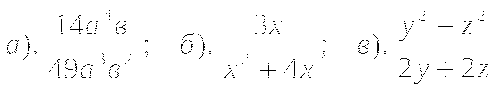
2). Постройте график функции .

Какова область определения функции? При каких значениях х функция принимает положительн

ые значения?

3). Докажите, что при всех значениях в ≠ ± 2 значение выражения

не зависит от х.

Контрольная работа № 3

1 вариант

1). Вычислите:

2). Найдите значение выражения:

3). Решите уравнение:

а). х² = 0,49; б). х² = 10; в). х² = - 25

4). Упростите выражение:

, где х ≥ 0;

, где в < 0.

5). Укажите две последовательные десятичные дроби с одним знаком после запятой, между которыми заключено число .

6). Имеет ли корни уравнение

2 вариант

1). Вычислите:

2). Найдите значение выражения:

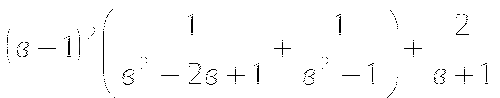
3). Решите уравнение:

а). х² = 0,64; б). х² = 17; в). х² = - 36

4). Упростите выражение:

, где у ≥ 0;

, где а < 0.

5). Укажите две последовательные десятичные дроби с одним знаком после запятой, между которыми заключено число .

6). Имеет ли корни уравнение

Контрольная работа № 4

1 вариант

1). Упростите выражение:

2). Сравните: и .

3). Сократите дробь:

4). Освободите дробь от знака корня в знаменателе:

5). Докажите, что значение выражения есть число рациональное.

2 вариант

1). Упростите выражение:

2). Сравните: и .

3). Сократите дробь:

4). Освободите дробь от знака корня в знаменателе:

5). Докажите, что значение выражения есть число рациональное.

Контрольная работа № 5

1 вариант

1). Решите уравнение:

а). 2х²+7х - 9 = 0;

б). 3х² = 18х;

в). 100 х² - 16 = 0;

г). х² - 16х + 63 = 0.

2). Периметр прямоугольника равен 20 см. Найдите его стороны, если известно, что площадь прямоугольника равна 24 см².

3). В уравнении х² + рх - 18 = 0 один из корней равен - 9. Найдите другой корень и коэффициент р.

2 вариант

1). Решите уравнение:

а). 3х²+13х - 10 = 0;

б). 2х² - 3х= 0;

в). 16 х² = 49;

г). х² - 2х - 35 = 0.

2). Периметр прямоугольника равен 30 см. Найдите его стороны, если известно, что площадь прямоугольника равна 56 см².

3). В уравнении х² + 11х + q = 0 один из корней равен - 7. Найдите другой корень и свободный член q.

Контрольная работа № 6

1 вариант

1). Решите уравнение:

2). Теплоход прошел 54 км по течению реки и 42 км против течения, затратив на весь путь 4 ч. Какова скорость теплохода в стоячей воде, если скорость течения реки равна 3 км/ч?

2 вариант

1). Решите уравнение:

2). Моторная лодка прошла 28 км против течения реки и 16 км по течению, затратив на весь путь 3 ч. Какова скорость моторной лодки в стоячей воде, если скорость течения реки равна 1 км/ч ?

Контрольная работа № 7

1 вариант

1). Докажите неравенство:

а). ( х - 2 )² > х( х - 4 );

б). а² + 1 ≥ 2( 3а - 4 ).

2). Известно, что а < в. Сравните:

а). 21а и 21 в; б). - 3,2а и - 3,2в;

в). 1,5в и 1,5а.

Результат сравнения запишите в виде неравенства.

3). Известно, что Оцените:

4). Оцените периметр и площадь прямоугольника со сторонами а см и в см, если известно, что:

2,6 < а < 2,7, 1,2 < в < 1,3.

5). К каждому из чисел 2, 3, 4 и 5 прибавили одно и то же число а. Сравните произведение крайних членов получившейся последовательности с произведением средних членов.

2 вариант

1). Докажите неравенство:

а). ( х - 2 )² > х( х - 4 );

б). а² + 1 ≥ 2( 3а - 4 ).

2). Известно, что а > в. Сравните:

а). 18а и 18 в; б). - 6,7а и - 6,7в;

в). - 3,7в и - 3,7а.

Результат сравнения запишите в виде неравенства.

3). Известно, что Оцените:

4). Оцените периметр и площадь прямоугольника со сторонами а см и в см, если известно, что:

1,5 < а < 1,6, 3,2 < в < 3,3.

5). Даны четыре последовательных натуральных числа. Сравните произведение первого и последнего из них с произведением двух средних чисел.

Контрольная работа № 8

1 вариант

1). Вычислите:

2). Упростить выражение:

.

3). Найдите , если известно, что

4). Упростить выражение:

5). Докажите тождество:

2 вариант

1). Вычислите:

2). Упростить выражение:

.

3). Найдите , если известно, что

4). Упростить выражение:

5). Докажите тождество:

Контрольная работа № 9

1 вариант

1). Вычислить:

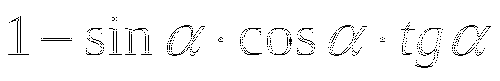
2). Решить уравнение:

а). 2х² + 7х - 9 = 0; в). 100х² - 16 = 0;

б). 3х² = 18х; г). х² - 16х + 63 = 0.

3). Упростить выражение:

4). Сократить дробь:

2 вариант

1). Вычислить:

2). Решить уравнение:

а). 7х² - 9х + 2 = 0; в). 7х²-28=0;

б). 5х² = 12х; г). х² + 20х + 91 = 0.

3). Упростить выражение:

4). Сократить дробь:

ГЕОМЕТРИЯ

Контрольная работа № 1.

1. 1 вариант.

1). Диагонали прямоугольника ABCD пересекается в точке О, ABO = 36°. Найдите AOD.

2). Найдите углы прямоугольной трапеции, если один из ее углов равен 20°.

3). Стороны параллелограмма относятся как 1 : 2, а его периметр равен 30 см. Найдите стороны параллелограмма.

4). В равнобокой трапеции сумма углов при большем основании равна 96°. Найдите углы трапеции.

5).* Высота ВМ, проведенная из вершины угла ромба ABCD обра­зует со стороной АВ угол 30°, АМ = 4 см. Найдите длину диагонали BD ромба, если точка М лежит на стороне AD.

2. 2 вариант.

1). Диагонали прямоугольника MNKP пересекаются в точке О,MON= 64°. Найдите ОМР. 2). Найдите углы равнобокой трапеции, если один из ее углов на 30° больше второго.

3). Стороны параллелограмма относятся как 3 : 1, а его периметр равен 40 см. Найдите стороны параллелограмма.

4). В прямоугольной трапеции разность углов при одной из боко­вых сторон равна 48°. Найдите углы трапеции.

5).* Высота ВМ, проведенная из вершины угла ромба ABCD обра­зует со стороной АВ угол 30°, длина диагонали АС равна 6 см. Най­дите AM, если точка М лежит на продолжении стороны AD.

Контрольная работа № 2.

1. 1 вариант.

1). Сторона треугольника равна 5 см, а высота, проведенная к ней, в два раза больше стороны. Найдите площадь треугольника.

2). Катеты прямоугольного треугольника равны 6 и 8 см. Найдите гипотенузу и площадь треугольника.

3). Найдите площадь и периметр ромба, если его диагонали равны 8 и 10 см.

4).* В прямоугольной трапеции АВСК большая боковая сторона равна 3см, угол К равен 45°, а высота СН делит основание АК пополам. Найдите площадь трапеции.

2 вариант.

1). Сторона треугольника равна 12 см, а высота, проведенная к ней, в три раза меньше высоты. Найдите площадь треугольника.

2). Один из катетов прямоугольного треугольника равен 12 см, а гипотенуза 13 см. Найдите второй катет и гипотенузу треугольника.

3). Диагонали ромба равны 10 и 12 см. Найдите его площадь и пе­риметр.

4).* В прямоугольной трапеции ABCD большая боковая сторона равна 8 см, угол А равен 60°, а высота ВН делит основание AD попо­лам. Найдите площадь трапеции.

Контрольная работа № 3.

1 вариант.

1). По рис. A = B, СО = 4, DO = 6, АО = 5.

Найти: а). ОВ; б). АС : BD; в). .

2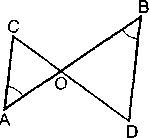). В треугольнике ABC сторона АВ = 4 см, ВС = 7 см, АС = 6 см, а в треугольнике MNK сторона МК = 8 см, MN =12 см, KN = 14 см. Найдите углы треуголь­ника MNK, если A = 80°, B = 60°.

3). Прямая пересекает стороны треугольника ABC в точках М и К соответственно так, что МК || АС, ВМ : АМ = 1 : 4. Найдите периметр треугольника ВМК, если периметр треугольника ABC равен 25 см.

4). В трапеции ABCD (AD и ВС основания) диагонали пересека­ются в точке О, AD = 12 см, ВС = 4 см. Найдите площадь треугольника ВОС, если площадь треугольника AOD равна 45 см^2.

2 вариант.

1). По рис. РЕ || NK, MP = 8, MN = 12, ME = 6. Найти: а) . МК; б). РЕ : NК; в). .

2). В ∆ АВС АВ = 12 см, ВС = 18 см, В = 70 ⁰, а в ∆ МNК МN = 6 см, NК = 9 см, N = 70 ⁰. Найдите сторону АС и угол С треугольника АВС, если МК = 7 см, К = 60 ⁰.

3). Отрезки АВ и CD пересекаются в точке О так, что ACO = BDO, АО : ОВ = 2:3. Найдите периметр треугольника АСО, если периметр треугольника BOD равен 21 см.

4). В трапеции ABCD ( AD и ВС основания) диагонали пересека­ются в точке О, = 32 см², = 8 см². Найдите меньшее осно­вание трапеции, если большее из них равно 10 см.

Контрольная работа № 4.

1 вариант.

1). Средние линии треугольника относятся как 2 : 2 : 4, а периметр треугольника равен 45 см. Найдите стороны треугольника.

2). Медианы треугольника ABC пересекаются в точке О. Через точку О проведена прямая, параллельная стороне АС и пересекаю­щая стороны АВ и ВС в точках Е и F соответственно. Найдите EF, если сторона АС равна 15 см.

3). В прямоугольном треугольнике ABC (C = 90° ) АС = 5 см, ВС = 5 см. Найдите угол В и гипотенузу АВ.

4). В треугольнике ABC A =, C =, сторона ВС = 7 см, ВН - высота. Найдите АН.

5). В трапеции ABCD продолжения боковых сторон пересекаются в точке К, причем точка В - середина отрезка АК. Найдите сумму оснований трапеции, если AD = 12 см.

1. 2 вариант.

1). Стороны треугольника относятся как 4 : 5 : 6, а периметр тре­угольника, образованного его средними линиями, равен 30 см. Най­дите средние линии треугольника.

2). Медианы треугольника MNK пересекаются в точке О. Через точку О проведена прямая, параллельная стороне МК и пересекаю­щая стороны MN и NK в точках А и В соответственно. Найдите МК, если длина отрезка АВ равна 12 см.

3). В прямоугольном треугольнике РКТ (T = 90° ), РТ = 7см, КТ = 1 см. Найдите угол К и гипотенузу КР.

4). В треугольнике ABC A = , C =, высота ВН равна 4 см. Найдите АС.

5). В трапеции MNKP продолжения боковых сторон пересекаются в точке Е, причем ЕК = КР. Найдите разность оснований трапеции, если NK = 7 см.

2. Контрольная работа № 5.

1 вариант.

1). АВ и АС - отрезки касательных, проведенных к окружности радиуса 9 см. Найдите длины отрезков АС и АО, если АВ = 12 см.

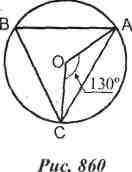2). По рисунку АВ : BC = 11 : 12.
Найти: BCA, BAC.

3). Хорды MN и РК пересека-

ются в точке Е так, что

ME = 12 см, NE = 3 см,

РЕ = КЕ. Найдите РК.

4). Окружность с центром О и

радиусом 16 см описана около треугольника ABC так, что угол OAB равен 30°, угол OCB равен 45°. Найдите стороны АВ и ВС тре­угольника.

2 вариант.

1). MN и МК - отрезки касательных, проведенных к окружности радиуса 5 см. Найдите MN и МК, если МО = 13 см.

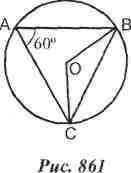2). По рисунку AB : АС=5 : 3.
Найти: BOC, ABC.

3). Хорды АВ и CD пересека -

ются в точке F так, что

AF = 4 см, ВF = 16 см, CF = DF. Найдите CD.

3. 4). Окружность с центром О и

4. радиусом 12 см описана около

5. треугольника MNK так, что угол MON равен 120°, угол NOK равен 90°. Найдите стороны MN и NK тре­угольника.

Примерный текст промежуточной аттестации по математике для 8 класса

Вариант № 1

Часть 1

Модуль «Алгебра»

1. Найдите значение выражения: (6,9 - 1,5) / 2,4.

Ответ: ___________________

2. Н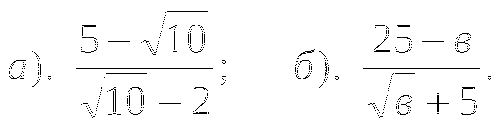а координатной прямой отмечены числа а и в

а в

• •

-1 0 1

Какое из следующих утверждений неверно?

1) -2< в - 1 < -1;

2) -а < 0;

3) а + в < 0;

4) а²в <0.

Ответ: ______________

3. В каком случае числа 2, 3 и 4 расположены в порядке возрастания?

1) 2; 4; 3;

2) 2; 3; 4;

3) 3; 4; 2;

4) 4; 2; 3.

Ответ? ____________

4. Решите уравнение: х² +7х - 18 = 0.

Ответ: _____________________

5. Установите соответствие между графиками функций и формулами, которые их задают.

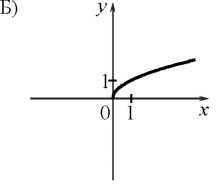
В)

1. 1) У=; 2) У=; 3) у=х²; 4) у=.

А

Б

В

6. Найдите наибольшее целое решение неравенства: 3х - 1 5(х + 2) - х.

Ответ: ___________________

7. Упростите выражение (а - 3)²-а(5а -6) и найдите его значение при а = - 0,5. В ответ запишите найденное значение.

8. В классе обучается 30 человек. С контрольной работой справились 90% учащихся. Сколько человек не справились с контрольной работой?

27; 2) 3; 3) 9; 4) 5.

Модуль «Геометрия»

9. Найдите угол ABC равнобедренной трапеции ABCD, если диагональ АС образует с основанием AD и боковой стороной CD углы, равные 30° и 80° соответственно.

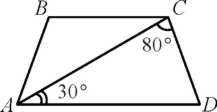
Ответ: ____________________

10.

Центральный угол АОВ равен 60°. Найдите длину хорды АВ, на которую он опирается, если радиус окружности равен 5.

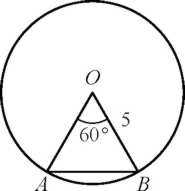
Ответ: _____________________

11. Найдите площадь параллелограмма, изображённого на рисунке.

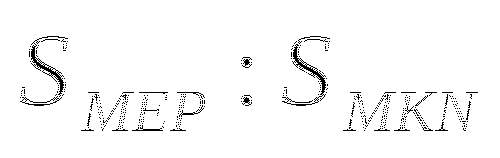
5 4

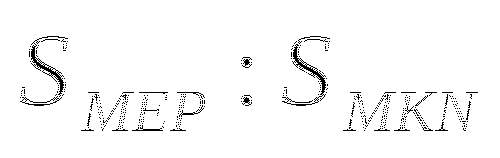
3 7

Ответ: __

12. Найдите тангенс угла А треугольника ABC , изображённого на рисунке.

13. Укажите номера верных утверждений.

1) Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.

2. Вертикальные углы равны.

3. Любая биссектриса равнобедренного треугольника является его медианой.

Модуль «Реальная математика»

14. Учёный Иванов выезжает из Москвы на конференцию в Санкт- Петербургский университет. Работа конференции начинается в 10:00. В таблице дано расписание ночных поездов Москва - Санкт-Петербург.

Номер поезда

Отправление из Москвы

Прибытие в Санкт-Петербург

026А

23:00

06:30

002А

23:55

07:55

038А

00:44

08:48

016А

01:00

08:38

Путь от вокзала до университета занимает полтора часа. Укажите номер самого позднего (по времени отправления) из московских поездов, которые подходят учёному Иванову.

1. 026А 2) 002А 3) 038А 4) 016А.

15. На рисунке изображён график изменения атмосферного давления в городе Энске за три дня. По горизонтали указаны дни недели, по вертикали - значения атмосферного давления в миллиметрах ртутного столба. Укажите наименьшее значение атмосферного давления во вторник.

762

760

758

756

754

752

750

16. Чашка, которая стоила 90 рублей, продаётся с 10%-й скидкой. При покупке 10 таких чашек покупатель отдал кассиру 1000 рублей. Сколько рублей сдачи он должен получить?

17. От столба высотой 9 м к дому натянут провод, который крепится на высоте 3м от земли (см. рисунок). Расстояние от дома до столба 8 м. Вычислите длину провода.

8м

18. На диаграмме представлено распределение количества пользователей некоторой социальной сети по странам мира. Всего в этой социальной сети 8млн пользователей.

- Россия

- Украина

- Беларусь

- Другие страны

Какое из следующих утверждений неверно?

1. Пользователей из России больше, чем пользователей из Украины.

2. Пользователей из Беларуси больше, чем пользователей из Швеции.

3. Больше трети пользователей сети - из Украины.

4. Пользователей из России больше 4 миллионов.

В ответе запишите номер выбранного утверждения.

Ответ:__________

19. Найдите моду ряда чисел 8, 23, 25, 14, 13, 15, 14, 71.

Ответ: _______

20. Найдите медиану ряда чисел 32, 41, 49, 30, 37, 42, 40, 45, 52.

Ответ: ____

Часть 2

21. Найдите наименьшее значение выражения (2х + у + 3)² + (3х - 2у + 8)² и значения х и у, при которых оно достигается.

Ответ:__________

22. При каких значениях параметра а уравнение (3а + 9)х² + ах - 1 = 0 имеет единственный корень?

Ответ: __________

23. Решите уравнение:

Ответ: _________

24. Упростите выражение: .

Ответ: _____________

25. Хорды АВ и CD пересекаются в точке Е. Найдите CD, если АЕ=4см, ВЕ=9см, а длина СЕ в четыре раза больше длины DE.

Ответ: ____________

26. Найдите площадь равнобедренного треугольника, боковая сторона которого равна 13 см, а основание 10 см.

Ответ: ____________

Вариант № 2

Часть 1

Модуль «Алгебра»

1. Найдите значение выражения: .

Ответ: __________________

2. Н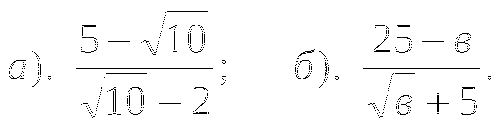а координатной прямой отмечены числа а и с.

а с

• •

-1 0 1

Какое из следующих утверждений неверно?

1) а - с >0;

2) -3< а + 1 < -2;

3) -с > -1;

4) <0.

Ответ: __________

3. В каком случае числа 4, 3 и 7 расположены в порядке возрастания?

1) 7; 4; 3;

2) 4; 3; 7;

3) 3; 7; 4;

4) 3; 4; 7.

Ответ: _____________

4. Решите уравнение: х² +2х - 15 = 0.

Ответ: _____________________

5. Установите соответствие между графиками функций и формулами, которые их задают.

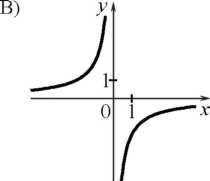
А)

1. у = х²; 2) у = -; 3) у = 2х; 4) у=..

Ответ:

А

Б

В

6. Найдите наибольшее целое решение неравенства: 4у - 9 3(у - 2) + 7у.

Ответ: _____________

7. Упростите выражение (а - 4)²-2а(5а -4) и найдите его значение при а =- . В ответ запишите найденное значение.

Ответ: _______________

8. В цехе работают 50 человек, 40 человек из них составляет молодёжь. Сколько процентов составляет молодёжь?

1) 92; 2) 80; 3) 0,8; 4) 60.

Модуль «Геометрия»

9. Найдите угол ABC равнобедренной трапеции ABCD, если диагональ АС образует с основанием AD и боковой стороной CD углы, равные 20° и 100° соответственно.

Ответ; __________________

10. Центральный угол АОВ равен 60°. Найдите длину хорды АВ, на которую он опирается, если радиус окружности равен 7.

Ответ: ___________

1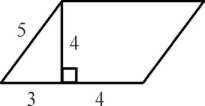1. Найдите площадь параллелограмма, изображённого на рисунке

Ответ: ________________

12. Найдите тангенс угла А треугольника ABC , изображённого на рисунке

Ответ: _______________

13. Укажите номера верных утверждений.

1. Если три угла одного треугольника равны трем углам другого треугольника, то такие треугольники подобны.

2. Сумма смежных углов равна 180° .

3. Любая медиана равнобедренного треугольника является его биссектрисой.

Ответ: _______________

Модуль «Реальная математика»

14. Бизнесмен Петров выезжает из Москвы в Санкт- Петербург на деловую встречу, которая назначена на 9:30. В таблице дано расписание ночных поездов Москва - Санкт-Петербург.

Номер поезда

Отправление из Москвы

Прибытие в Санкт-Петербург

038А

00:43

08:45

020У

00:54

09:02

016А

01:00

08:38

116С

01:00

09:06

Путь от вокзала до места встречи занимает полчаса. Укажите номер самого позднего (по времени отправления) из московских поездов, которые подходят учёному Иванову.

1)038А; 2) 020У; 3) 016А; 4) 116С.

Ответ: _________

15. На рисунке изображён график изменения атмосферного давления в городе Энске за три дня. По горизонтали указаны дни недели, по вертикали - значения атмосферного давления в миллиметрах ртутного столба. Укажите наименьшее значение атмосферного давления в среду.

762

758

754

750 вторник среда четверг

Ответ: _______________________

16. Тарелка, которая стоила 80 рублей, продаётся с 10% - ой скидкой. При покупке 10 таких тарелок покупатель отдал кассиру 1000 рублей. Сколько рублей сдачи он должен получить?

Ответ: ___________________

17. От столба высотой 9 м к дому натянут провод, который крепится на высоте

4м от земли (см. рисунок). Расстояние от дома до столба 12 м. Вычислите длину провода.

Ответ: ________________

18. На диаграмме представлено распределение количества пользователей некоторой социальной сети по странам мира. Всего в этой социальной сети 9 млн. пользователей.

- Россия

- Украина

- Беларусь

- Другие страны

Какое из следующих утверждений неверно?

1. Пользователей из России меньше 4 миллионов.

2. Пользователей из Украины меньше трети общего числа пользователей.

3. Пользователей из Беларуси больше, чем пользователей из Дании.

4. Пользователей из России больше, чем пользователей из Беларуси.

В ответе запишите номер выбранного утверждения.

Ответ: _________________

19. Найдите размах ряда чисел 3, 17, 24, 9, 15, 71, 56.

Ответ: ______________

20. . Найдите моду ряда чисел 18, 23, 13, 14, 13, 15, 13, 72.

Ответ: ______________

Часть 2

При выполнении заданий 21-26 используйте бланк ответов № 2. Сначала укажите номер задания, а затем запишите его решение и ответ. Пишите чётко и разборчиво. Обращаем Ваше внимание на то, что записи в черновике не будут учитываться при оценивании работы.

21. Найдите наименьшее значение выражения (2х - 3у - 1)² + (3х + у - 7)² и значения х и у, при которых оно достигается.

Ответ: _______________

22. При каких значениях параметра в уравнение (в + 1)х² + вх - 1 = 0 имеет единственный корень?

Ответ: ______________

23. Решите уравнение: .

Ответ: ______________

24. Упростите выражение: .

Ответ: ____________

25. Хорды MN и KP пересекаются в точке Т. Найдите MN, если КТ=6см, РТ=8см, а длина МТ в три раза меньше длины NT.

Ответ: ______________

26. Сторона ромба равна 8 см, а один из углов равен 150^о Найдите площадь ромба.

Ответ: _______________