'Квадратные неравенства'

ГОУ ВПО «МордГПИ им. М. Е. Евсевьева»

Конспект

урока по алгебре

в 8 классе

Тема «Квадратные неравенства»

Подготовила: Прохорова С.

Проверила: Сафонова Л. А.

Тема урока:Квадратные неравенства.

Тип урока: Обобщение и контроль знаний.

Цели и задачи урока:

• обеспечить в ходе урока повторение и закрепление пройденного материала,

• закрепить умение решать квадратные неравенства,

• ознакомить учащихся с видами заданий повышенной сложности

• развитие навыков само- и взаимоконтроля,

• развитие навыка самостоятельной работы,

• воспитаниеаккуратности, создание атмосферы доброжелательности и активного творческого труда.

Оборудование:раздаточный материал, презентация.

Ход урока:

1. Организационный момент.

2. Повторение.

Ученики смотрят видео решения квадратных уравнений графическим методом и методом интервалов, а затем отвечают на вопросы (видеоматериалы представлены в презентации (слайд 2 и слайд 4)).

Теоретический опрос:

• Как решить неравенство методом интервалов?(слайд 3)

(1. найти корни соответствующего квадратного уравнения

или установить, что их нет;

2. отметить корни на числовой прямой;

3. в крайнем правом интервале поставить знак, соответствующий

знаку коэффициента a квадратного трехчлена;

4. расставить знаки на остальных интервалах в порядке чередования;

5. определить промежутки, на которых функция принимает нужные

Значения).

• Как решить неравенство графическим способом? (слайд 5)

(1. определить направление ветвей параболы

по знаку коэффициента а;

2. найти корни соответствующего квадратного уравнения

или установить, что их нет;

3. построить эскиз графика квадратичной функции;

4. по графику определить промежутки, на которых

функция принимает нужные значения).

• Какие неравенства называются квадратными?(слайд 6)

(Неравенства, у которых в левой части стоит квадратный трехчлен, а в правой нуль.)

• Какие способы решения квадратного неравенства мы знаем?

( Квадратное неравенство можно решить графическим способом и методом интервалов).

• Что значит решить неравенство?

(Решить неравенство- это значит найти все его решенияили установить, что их нет).

(После каждого ответа ученика, определения и алгоритмы выводятся на слайдах).

3. Разминка. (слайд 7)

На карточках и на слайде представлены 3 квадратных неравенства, решенных графическим способом и методом интервалов, с ответами. Ученикам предлагалось найти, объяснить и исправить ошибки в ответах. В одном случае ошибки не было.

(При нажатии на неравенство, под ним появляется надпись «верно»\ «неверно»).

4. Решение неравенств с готовым выбором ответов. (слайд 8)

На карточках по вариантам предлагается 4 неравенства и готовые ответы. Ученики решают неравенства, выбирают правильный ответ из предложенных и заполняют таблицу соответствия. После решения они обменивались карточками с соседом по парте и проверяли его работу.

1 вариант

А х² - 9 > 0; 1) [ 0 ; 2 ]

Б - х ² + 2х ≥ 0; 2) (- ∞; - 3) (3; +∞)

В х² - х - 6 < 0; 3) (- ∞; - ⅓] [1; +∞)

Г - 3х² + 2х + 1 ≤ 0; 4) (-3; 2)

2 вариант

А - х ² + 3х < 0; 1) (-1; 2,5)

Б х² - 4 ≤ 0; 2) (- ∞; - 0) (3; +∞)

В х² - 3х - 4 ≥ 0; 3) [ - 2 ; 2 ]

Г -2х² + 3х + 5 > 0; 4) (- ∞; - 1] [4 ; +∞)

Правильные ответы (слайд 9):

1 вариант

А

Б

В

Г

2

1

4

3

2 вариант

А

Б

В

Г

2

3

4

1

(Все 2 варианта представлены на слайде.При нажатии на каждое неравенство, напротив него появляется правильный ответ).

5. Самостоятельная работа.

Ученики выбирают из 3 вариантов разного уровня сложности (карточки разного цвета).

1 уровень

Решить неравенства:

3 х ² ≥ 75

8 х - х ²> 0

- х ² - 4 х + 5 х ²< 0

2 х ² - 3 х - 5 ≤ 0

2 уровень

Решить неравенства:

( х - 1) (3 - 2х) > - 6

(х + 2) (2 - х) ≤ 3 х ² - 8

≤

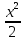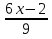
3 уровень

Укажите целые решения неравенства 4 - х ² > (2 + х)²

Назовите наименьшее целое положительное решение неравенства - x²<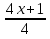

При каких х выражение 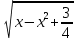имеет смысл?

(Карточки с листочками сдаются на проверку. Если ученик выполняет все задания из 1 уровня, два задания из 2 уровня и хотя бы одно задание из 3 уровня, то оценка «5»; если ученик выполняет все задания из 1 уровня и хотя бы два задания из 2 уровня, то оценка «4»; если ученик выполняет только первый уровень, то оценка «3»; если первый уровень выполнен с ошибками, то оценка «2»).

6. Домашнее задание: №687-691(3), Проверь себя!(стр191). (слайд 10)

7. Подведение итогов урока. (слайд 11)

Ученикам предлагается ответить на несколько вопросов по уроку.

(Вопросы представлены на слайде).

Литература:

1. «Алгебра 8 класс», учебник, под редакцией А.Г. Мордковича, Мнемозина, 2007 г.

2. «Алгебра 8 класс», задачник, под редакцией А.Г. Мордковича, Мнемозина, 2007 г.

3. «Тематический сборник тестовых заданий по алгебре для подготовки к государственнойаттестации в новой форме», базовый уровень, под редакцией Е.А. Семенко, Просвещение-Юг, Краснодар, 2008 г.