Учителю
Метапредметный урок по геометрии 7 класса на тему: 'Внешний угол треугольника'

Метапредметный урок по геометрии 7 класса на тему: 'Внешний угол треугольника'

Автор публикации: Устинова Н.В.

Дата публикации: 26.02.2015

Краткое описание: В основе сценария по геометрии лежит метапредмет "Задача". В традиционной педагогической практике задача - средство отработки теоретической части, форма контроля выявления уровня реально усвоенного. Сила психологического подхода - в выявлении средств, имеющихся у учени

предварительный просмотр материала

Класс: 7

Предметная тема: Внешний угол треугольника

Образовательная область: геометрия

Этап обучения по данной теме: ознакомительный

Метапредмет: Задача

Метапредметная тема: Знание и информация

Актуальность данного учебного занятия состоит в том, что на сегодняшний день подросток вынужден быстро ориентироваться в информационном пространстве и уметь решать проблемные задачи. Ему надо научиться из потока информации выбирать необходимую и преобразовать ее в знание.

Метапредметная цель учебного занятия: сформировать понятие и вывести свойство внешнего угла треугольника в процессе отбора нужной информации путем применения ранее полученных знаний.

Учебная цель: ввести понятие внешнего угла треугольника.

Цели урока:

обучающая: создать условия для усвоения понятия внешнего угла треугольника и применения его свойства при решении задач; проверка знаний учащихся фактического материала, умений учащихся применять знания в стандартных условиях, а также в измененных нестандартных условиях.
развивающая: развивать умение выбирать из потока информации необходимую для решения математических задач;
воспитательная: воспитывать умение работать в парах и самостоятельно.

Оборудование и материалы: карточки с заданиями, ОС Windows , презентация Microsoft Power Point, мультимедийный проектор/плазма.

Ход урока

I. Мобилизующий этап

Ребята, я всегда считала, что «Знание - сила». Но в интернете обнаружила в одной статье такое мнение, что эта фраза (принадлежащая знаменитому английскому философу Фрэнсису Бэкону (1561-1626)) сейчас потеряла свою актуальность в связи с появлением современных средств массовой информации. Зачем нужны знания, когда все можно найти в Интернете?

Вопросы классу:

- А как вы считаете, потерялось ли значение фразы «Знание - сила»? (ответы учащихся)

- Согласны ли вы с мнением автора статьи?

Сегодня на уроке геометрии мы попробуем разобраться, действительно ли потерялось значение этого выражения?

Тема нашего урока - «Знание и информация». А тему по геометрии запишем чуть позже, оставьте строку.

II. Преобразование информации в знание

- В словарях Даля, Ожегова, Ефремова об этом понятии можно прочитать следующее:

перелом, излом, колено, локоть, выступ или залом.
Место, где сходятся, пересекаются два предмета или две стороны чего-либо.
Место, где сходятся внешние стороны предмета.
Место пересечения двух улиц.
Место, где сходятся внутренние стороны предмета.
Часть предмета, заключенная между такими сторонами.
Часть помещения между двумя сходящимися стенами.

Как вы считаете, о чем идет речь? (ответ учащихся: угол)

- Мы с вами изучили много видов углов. Давайте сейчас их вспомним (возможные ответы учащихся: развернутый угол, острый угол, смежные углы, накрест лежащие углы, прямой угол, вертикальные углы, соответственные углы, тупой угол, односторонние углы).

- Молодцы, ребята, вы перечислили все виды углов. Те углы, которые вы назвали, нарисованы на листочках, которые лежат у вас на столе. ()

Задание классу: К каждому рисунку поставьте в соответствие название угла с правой стороны. Он зашифрован одной буквой. При правильном выполнении задания у вас получится слово (компьютер).

С появлением компьютеров стало возможным получать потоки информации. Вы сейчас тоже из множества информации выбрали необходимую, показали свои знания.

- Мы с вами повторили все виды углов, какие вы знаете. Но у нас остался еще один угол без названия, под №10. Возвращаемся снова к словарю Ефремова: место, где сходятся внутренние стороны предмета; место, где сходятся внешние стороны предмета - о каких углах идет речь? (возможные ответы учащихся: внутренний угол треугольника, внешний/наружный угол треугольника). В словаре Даля по этому поводу сказано: угол одинаково прилагается ко внутреннему простору, ко впадине, и ко внешнему очертанью, выступу; первое внутренний угол, второе наружный; угол выступом, выступной, и угол заломный, заходный, впалый.

Посмотрите на рисунок на экране:

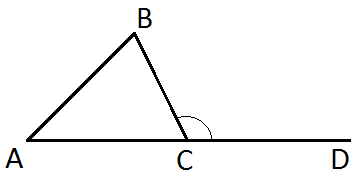
Вопросы по рисунку:

- Какие виды углов есть на рисунке?

- Назовите угол смежный с углом АСВ (ответ учащегося: DСВ), каким он будет по отношению к треугольнику? (возможный ответ учащихся: наружный, внешний).

- У нас появляется новый вид угла. Как мы можем назвать его?

Значит, тема нашего урока по геометрии - «Внешний угол треугольника».

Попробуем дать определение внешнего угла треугольника, что такое внешний угол треугольника?

У вас на столах есть листочек, на котором прописаны словосочетания и предложения. ()

Задание классу: Выбрать те словосочетания или предложения, из которых сложится определение внешнего угла треугольника. Записывать определение не нужно, надо записать только цепочку из цифр, глядя на рисунок внешнего угла треугольника

(Проверка и запись цепочки на доске у нескольких учеников).

Чтобы получить точное определение, мы сейчас используем один из 5 видов информации - цифровой: 1→3→6→8 и логическую цепочку. Итак, сформулируем определение внешнего угла треугольника и запишем его в тетрадь. Прочитайте, что вы записали (Внешний угол треугольника при данной вершине - это угол, с внутренним углом треугольника при этой вершине). Мы с вами только что использовали текстовый и звуковой виды информации.

Чтобы удостовериться, что получено правильное, точное определение, обратимся к учебнику. Сравним наше определение с данным в учебнике (работа с учебником)

Вопрос классу:

- Как вы думаете, сколько внешних углов имеет треугольник? (после ответа учащихся).

Итак, ребята, получая определение внешнего угла треугольника, мы с вами включили мыслительную деятельность. А полученную информацию превратили в знание.

Вопрос классу:

- Как вы считаете, владея только информацией об определении внешнего угла треугольника, мы можем решать задачи? Нам этой информации достаточно? (ответы учащихся).

III. Понимание условий

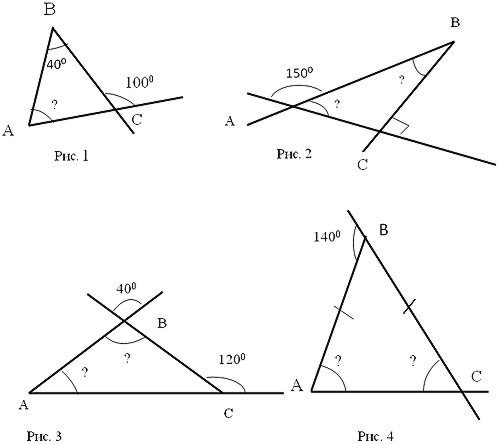
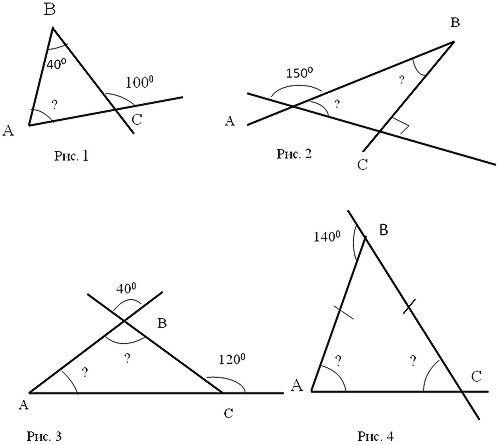
Давайте с вами попробуем устно решить довольно простые задачи по нахождению неизвестных углов треугольника:

Решение учащихся выполняется в 2 действия: сначала находится угол, смежный с внешним, затем искомый.

- Как видим, для устного решения задачи оказались немного сложными. Значит, нам нужна еще «информация» о внешнем угле треугольника. А эту информацию мы получим в ходе выполнения лабораторной работы.

IV. Моделирование отношений величин

Задание классу: (парная работа)

- На столах инструкции лабораторной работы (рисунок к лабораторной работе в помощь учащимся вывести крупным планом на экран).

- Построение и измерения выполняйте прямо на листочках в таблице, а вывод запишите в тетрадь ().

Вопрос классу: Прочитайте, какой вывод вы записали? (Внешний угол треугольника равен сумме двух углов, не смежных с ним).

Мы с вами получили свойство внешнего угла треугольника.

Итак, выполняя лабораторную работу, мы использовали «информацию» для получения свойства внешнего угла треугольника, которую преобразовали в знание. Мы говорим «информация», «знание». А как вы понимаете эти понятия?

Вопрос классу:

- Что такое информация? (Информация - это данные и сведения, представленные в различном виде).

- Что такое знание? (Знание - это обладание проверенной информацией, позволяющей решить поставленную задачу).

Мы с вами применяли различные виды информации, старались выбирать необходимую. Правильно выбранную информацию использовали для получения определения и свойства внешнего угла треугольника. А значит, превратили ее в знание. И сейчас полученные знания будем использовать в ходе решения задач по готовым чертежам. При этом воспользуемся еще одним видом информации - графическим.

V. Выдвижение способа

Давайте вернемся к задачам, решенным ранее. Обратите внимание, используя свойство внешнего угла треугольника, эти задачи решаются в одно действие. А как вы справитесь со следующей задачей?

VI. Реализация способа преобразования информации в знания

И еще несколько задач:

VII. Итог урока

А сейчас вернемся к началу урока. Нужны ли знания в настоящее время? Потерялось ли значение фразы: «Знание - сила» ? Не всякая информация является знанием. Нужно правильно выбирать и применять ее. Знания сохраняются долго, мы можем использовать их в любое время, а информация приходит и уходит быстро. Знание - это клад, а умение учиться - ключ к нему.

Домашнее задание. Решите задачу: В наличии имеется декоративная плитка различной треугольной формы в виде равнобедренных треугольников четырех видов. Составьте рисунки из такой плитки, если внешние углы при основании треугольников соответственно равны 150, 135, 120, 110. Сколько решений имеет задача?

VIII. Рефлексия

Продолжите предложения:

Я на уроке узнал…………………….……
Мне на уроке понравилось……………….
Меня удивило, что………………………..
В дальнейшем я …………………………

Урок закончим китайской мудростью:

Скажи мне - и я забуду;

Покажи мне - и я запомню;

Дай мне действовать самостоятельно - и я научусь.

IX. Литература

1. http://festival.1september.ru/mathematics/ Метапредметный урок "Внешний угол треугольника". 7-й класс - , учитель математики

2. Алексеев Н.Г. «Рефлексия и формирование способа решения задач»// Диссертация на соискание ученой степени кандидата психологических наук.- М., 2002 (переиздание)

3. Щедровицкий Г.П. «Исследование мышления детей на материале решений простых, арифметических задач»// Развитие познавательных и волевых процессов у дошкольников.- М., 1965

4. Т.Ф. Ефремов Новый словарь русского языка. Толково- словообразовательный online

5. В.Даль Толковый словарь живого великорусского языка (онлайн версия).

Приложение 1