Урок в 8 классе

Урок математики в 8 классе.

Тема урока: «Решение квадратных неравенств

Цели урока.

Образовательные:

• Ввести понятие квадратичных неравенств

• Познакомить с алгоритмом решения неравенств на основе свойств квадратичной функции.

• Сформировать умения решать неравенства данного вида.

Развивающие:

• Выработать умения анализировать, выделять главное, сравнивать, обобщать.

• Формировать графическую и функциональную культуру учащихся.

Воспитательные:

• Показать взаимосвязь математики с окружающей действительностью.

• Формировать навыки общения, умения работать в коллективе.

Оборудование:

• Интерактивная доска

• Презентация к уроку

• Раздаточный материал

Ход урока

I. Организационный момент

Сегодня мы с вами познакомимся с еще одним видом неравенств с одной переменной. Но прежде, давайте проверим себя, всё ли было усвоено на уроках, имеются ли слабые места. Для этого проведём разминку по изученному материалу.

ΙΙ. Актуализация (работа в парах).

1. Соотносите квадратные трехчлены с их корнями (Приложение 1)

А) 1)

Б) 2)

В) 3) ОТВЕТЫ

А

Б

В

Г

4

1

2

3Г) 4)

А

Б

В

Г

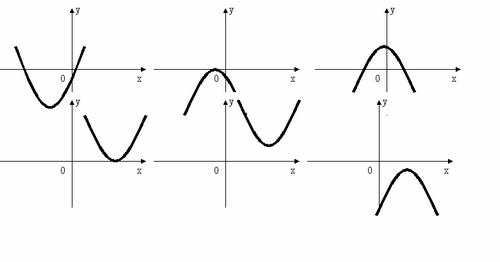
2. Запишите, какие знаки имеет старший коэффициент и дискриминант для каждой из парабол. (Приложение 2)

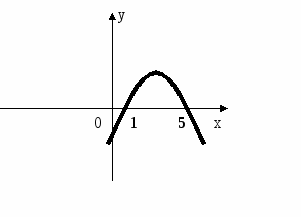
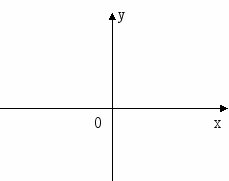
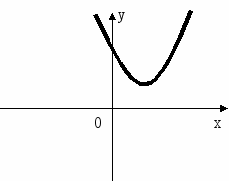
3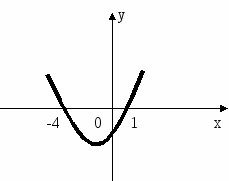. По графику квадратичной функции укажите все значения аргумента, при которых:

1

-4

(Приложение 3)

Мы с вами повторили ранее изученный материал, который нам сегодня еще пригодится

III Новая тема

Мы с вами умеем строить график квадратичной функции, умеем решать квадратные уравнения, а сегодня мы должны научиться решать неравенства второй степени с одной переменной.

• Итак, какой формулой задаётся квадратичная функция?

• Какой вид имеет квадратное уравнение?

• Какой вид имеет квадратный трёхчлен?

• Как вы думаете, какой вид будет иметь неравенство второй степени с одной переменной?

Попробуйте сформулировать определение.

Определение: Квадратным называется неравенство, левая часть которого − квадратный трёхчлен, а правая часть равна нулю.

, , ,

(записывают в тетрадь)

Мотивация. Попробуем выяснить, а где в окружающей нас среде встречаются квадратичные неравенства. Для этого вы сейчас объединитесь в группы по 4 человека (из двух соседних парт). Я раздам вам задачи, к которым вы попробуйте составить неравенство данного вида.

(Приложение 4)

1. Зависимость объема спроса q (единиц в месяц) на продукцию предприятия - монополиста от цены р (тыс.руб.) задается формулой q=100-10р. Выручка предприятия за месяц r (в тыс. руб.) вычисляется по формуле r(р) = q · р. Определите наибольшую цену р, при которой месячная выручка r(р) составит не менее 240 тыс.руб.

Ответ:

2. Высота над землей подброшенного вверх мяча меняется по закону h(t) = 1,6 + 8t -5t² , где h - высота в метрах, t - время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте не более трех метров? Ответ:

3. Высота струи воды у фонтана определяется по формуле , h- высота подъема воды над землей в метрах; v₀ - начальная скорость; g - ускорение свободного падения; h₀ - начальная высота струи, α - угол наклона струи. Фонтан лучше смотрится, если капли воды достигают высоты большей, чем высота статуи. Определите наименьшую начальную скорость струи фонтана, если высота статуи 3 м и угол наклона струи 60⁰.

Ответ:

Видим, что квадратные неравенства встречаются в разных сферах (физика, архитектура, экономика и т.д.)

А как же мы будем их с вами решать? Для этого существует специальный алгоритм, который мы с вами сейчас разберем на конкретном примере (записывают в тетрадь).

Алгоритм решения квадратных неравенств Решите неравенство

1. Приведите неравенство к виду

1.

2. Рассмотреть функцию

2. . Графиком данной функции является парабола, ветви которой направлены вверх

3. Найти корни квадратного трехчлена

3., х₁=-1, х₂=4

4. Отметить найденные корни на оси х и схематически построить график рассматриваемой функции; выделите те, значения х, при которых у<0 (>0)

4

4

-1.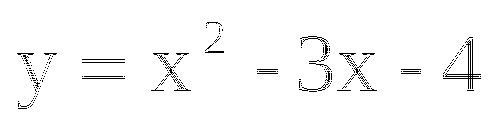

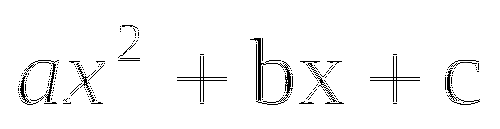
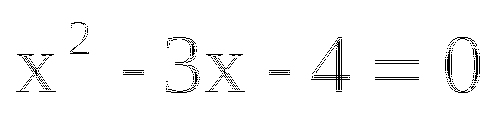
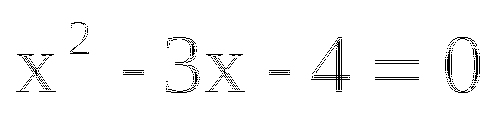
5. Запишите ответ

5. ответ:

Применение знаний, формирование умений и навыков

А теперь закрепим этот алгоритм.

1. Для этого вам нужно заполнить пропуски в таблице, которая у вас лежит на парте (индивидуальная работа, затем все вместе обсуждаем и проверяем)). (Приложение 6)

Решить неравенство х² - 3х +2<0

Рассмотрим функцию…

Графиком данной функции

является… , ветви направлены…

х² - 3х +2=0

х₁=… х₂=...

х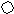

Ответ:

Решите неравенство - х² - 3х 0

Рассмотрим функцию…

Графиком данной функции

является… , ветви направлены…

- х² - 3х = 0

х₁=… х₂=...

х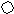

Ответ:

2. Класс (один ученик у доски) решает неравенство по алгоритму. Учитель контролирует.

а) ответ:

б) ответ:

3.Обучающая самостоятельная работа.

Предлагается решить 3 неравенства, затем на доске показываются правильные ответы, для того, чтобы учащиеся могли проверить свои решения. Во время решения учащиеся консультируются с учителем. Те, кто успешно справится с решением, получат оценки.

Вариант 1 Вариант 2

а) х²-9>0; а) х²-16<0;

б) х²-8х+15<0; б) х²-10х+21>0;

в) -х²-10х-25>0. в) -х²+6х-9>0.

Правильные ответы:

Вариант 1 Вариант 2

а) (-∞;-3)(3;+∞); а) (-4;4);

б) (3;5); б) (-∞;3)(7;+∞);

в) решений нет. в) решений нет.

IV. Итог урока. Домашнее задание

Подведение итогов.

-Какова была цель нашего урока?

-Сформулируйте определение неравенств второй степени с одной переменной.

-Как решать такие неравенства?

-Алгоритм решения.

Домашнее задание: