- Учителю
- «Апелляция – как способ формирования успешной подготовки к ЕНТ»
«Апелляция – как способ формирования успешной подготовки к ЕНТ»
«Ұзынкөл ауданының білім беру бөлімі» мемлекеттік мекемесінің «Суворов орта мектебі» коммуналдық мемлекеттік мекемесі Коммунальное государственное учреждение «Суворовская средняя школа» государственного учреждения «Отдел образования Узункольского района»
Материал для публикации: «Апелляция - как способ формирования успешной подготовки к ЕНТ »

Математика мұғалімі: Керейбаева Ғайни Сәдірқызы
Учитель математики: Кирибаева Гайни Садировна
«Апелляция - как способ формирования успешной подготовки к ЕНТ»
Вопросы, представленные в базе данных ЕНТ, до последнего времени вызывают справедливые нарекания. Диапазон претензий достаточно широк - от откровенных ошибок до включения вопросов, вызывающих дискуссии в современном мире науки.
Словарь иностранных слов сообщает, что слово «апелляция» пришло к нам из латинского языка и имеет несколько лексических значений. Первое значение - «обжалование какого-либо постановления в высшие инстанции». Второе - означает одну из форм «обжалования судебного решения в высшие судебные инстанции, то есть кассацию». Третье значение слова звучит так: «обращение за советом, поддержкой». Говоря об апелляции в нужном нам смысле, не надо забывать о последнем значении этого слова.
Для разрешения спорных вопросов при оценке тестовых заданий, защиты прав участников ЕНТ на период проведения тестирования создается республиканская комиссия по рассмотрению апелляций; в каждом пункте проведения ЕНТ работает апелляционная комиссия, в которой выпускники имеют право оспорить результаты ЕНТ. Необходимым условием успешности апелляции является грамотно составленное заявление. Дело в том, что апелляционная комиссия руководствуется в своих действиях инструкцией, которая регулирует порядок подачи и рассмотрения апелляционных заявлений.
Процесс подачи апелляционного заявления прост, но требует от ученика твердости и уверенности.
Наша задача: заранее познакомить учащихся со своими правами, настроить на твердое отстаивание своей позиции. На этапе непосредственной подачи заявления ученик будет отстаивать свои интересы самостоятельно, но перед этим он должен получить помощь учителя.
Работы не выдают «во временное пользование», и уж тем более не разрешают брать домой. Учащихся надо настроить на следующие действия:
●записать на имеющийся листок спорные вопросы и их номера.
Это очень важно, так как членам апелляционной комиссии категорически запрещено рассматривать вопросы, не указанные в заявлении.
Для того, чтобы ученик сориентировался в выборе тех вопросов, которые могут принести добавочные баллы, необходимо еще во время подготовки к ЕНТ обращать внимание на подобные вопросы. Ученик должен твердо знать, вопросы какого типа позволяют подавать на апелляцию.
Министерская комиссия признает в качестве доказательств только рекомендованные МОН РК учебники и пособия по подготовке к единому национальному тестированию.
Заявление от выпускника на апелляцию по содержанию тестового задания принимаются во время проведения тестирования по установленной форме (форма Е-24).
Апелляция по содержанию тестового задания подается, если:
●нет правильного ответа;
●несколько правильных ответов;
●некорректное тестовое задание.
Заявления от выпускников на апелляцию по технической причине в установленной форме (форма Е-25)принимаются после объявления результатов до 13 часов следующего дня.
Апелляция по технической причине подается, если:
●закрашен один кружок, совпадает с кодом правильных ответов, но сканер принял как два закрашенных кружка;
●закрашен один кружок, совпадает с кодом правильных ответов, но не считывается сканером.
Учитель должен в течение учебного года готовить ученика к внимательному прочтению тестовых вопросов во время пробных тестирований, к подаче апелляции, помогать составить заявление, систему доказательств. Важно не просто объяснить ребенку его правоту, но подкрепить это соответствующей учебной литературой, указать авторов учебника, страницу, год издания, все выходные данные, при необходимости можно сделать ксерокопию необходимых материалов.
Второго шанса доказать свою правоту у выпускника не будет, так что ему нужно постараться грамотно, аргументировано и последовательно защитить свою работу по всем намеченным позициям. Здесь сыграют большую роль точные знания, грамотные ссылки на первоисточники, умение вовремя сориентироваться, трактовать спорные моменты в свою пользу.
На этапе апелляции учащийся должен чувствовать себя уверенно, уметь вежливо, но твердо настоять на своем.
Таким образом, для того, чтобы апелляция стала действенным фактором повышения качества результатов тестирования, необходима серьезная консультация и профессиональная помощь учителя.
Вопросы, которые позволяют подавать на апелляцию. 1. 2007. Сборник тестов по математике. Вариант 9, №25 Решите неравенство: 3x2 > 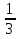 A) xЄ(-3;3) B) xЄ(-∞;0)U(3;+ ∞) C) xЄ(-3;0)U(0;3) D) xЄ(-∞;-3)U(3;+∞) E) xЄ(-∞;-3)U(0;3)
A) xЄ(-3;3) B) xЄ(-∞;0)U(3;+ ∞) C) xЄ(-3;0)U(0;3) D) xЄ(-∞;-3)U(3;+∞) E) xЄ(-∞;-3)U(0;3)
Решение: 3x2 > 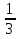
3x2 : 3 > 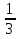 : 3
: 3
x2 > 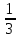 x2 -
x2 - 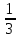 > 0 (x -
> 0 (x -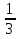 ) (x +
) (x +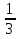 ) > 0
) > 0
![]()
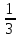
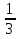 Ответ: xЄ(-∞; -
Ответ: xЄ(-∞; -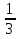 ) U (
) U (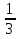 ;+∞) В вариантах ответов нет ни одного правильного ответа. 2. Вариант 1582, №26. Маша и Юля собирали грибы. - Юля, сколько у тебя грибов? - спросила Маша. - 30, ответила Юля. - А у тебя? - Столько же, как у тебя и ещё треть всех. Сколько грибов у Маши? A) 50. B) 40. C) 80. D) 60. E) 30. Решение: Случай 1: треть всех грибов, собранных только Юлей.
;+∞) В вариантах ответов нет ни одного правильного ответа. 2. Вариант 1582, №26. Маша и Юля собирали грибы. - Юля, сколько у тебя грибов? - спросила Маша. - 30, ответила Юля. - А у тебя? - Столько же, как у тебя и ещё треть всех. Сколько грибов у Маши? A) 50. B) 40. C) 80. D) 60. E) 30. Решение: Случай 1: треть всех грибов, собранных только Юлей.
1) 30 : 3=10 (г.); 2) 30 + 10 =40(г.). Ответ: 40 грибов.
Случай 2: треть всех грибов, собранных Юлей и Машиных стольких же грибов, как у Юли.
1) 30 + 30 =60 (г.); 2) 60 : 3=20 (г.); 3) 30 + 20 =50 (г.). Ответ: 50 грибов.
Случай 3: треть всех грибов, собранных Юлей и Машей вместе. Решение: Пусть Юля и Маша вместе собрали x грибов.
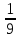 х г.
х г.
30 + (30 + 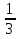 х) = х
х) = х
30 + 30 + 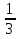 х = х
х = х
30 + 30 = х - 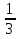 х
х
60 = 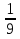 х
х
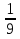 х = 60
х = 60
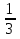
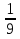 х = 60∙
х = 60∙ 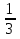 х = 90
х = 90
30 + 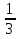 х = 30 +
х = 30 + 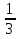 ∙ 90 = 60
∙ 90 = 60
Ответ: 60 грибов.
Некорректное задание. Непонятно, треть всех каких грибов: собранных только Юлей или треть всех грибов, собранных Юлей и Машиных стольких же грибов или собранных Юлей и Машей вместе. Правильный ответ: В) или А) или Д)
3. 2006. Математика бойынша тест жинағы. 4 нұсқа, №18 В геометрической прогрессии S2=4, S3 =13. Найдите S4. A) 40. B) 25. C) 40, 235/16. D) 25/16. E) 40, 25/4. Решение: S2=b1+b2=b1+b1g=b1(1+g) S3= b1+b2+b3= S2+ b1g2 b1(1+g)= S2 S2+ b1g2= S3 b1(1+g)=4 4+ b1g2= 13 b1= 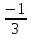 b1g2= 9
b1g2= 9
b1= 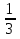
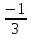 =
= 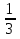 4g2= 9(1+g) 4g2= 9+9g 4g2- 9g - 9=0 D=(-9)2 - 4∙4∙(-9)=81+144=225>0
4g2= 9(1+g) 4g2= 9+9g 4g2- 9g - 9=0 D=(-9)2 - 4∙4∙(-9)=81+144=225>0
g1= 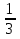 =
= 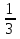 = -
= - 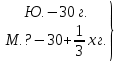 b1= 9: (g1)2=9: (-
b1= 9: (g1)2=9: (- 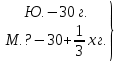 )2=9:
)2=9: 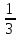 =9∙
=9∙ 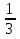 =16 g2=
=16 g2= 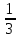 =3 b2= 9: (g2)2=9:32=1
=3 b2= 9: (g2)2=9:32=1
b1 (g1)3=16∙ (- 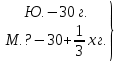 )3=16∙ (-
)3=16∙ (- 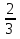 )=-
)=- 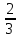 =-6
=-6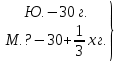
b2∙ (g2)3=1∙33=27 S4=S3+b4=S3+ b1 (g1)3=13+(-6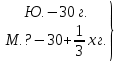 )=12
)=12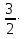 - 6
- 6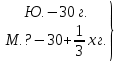 =6
=6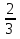 =
= 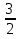 или S4=S3+b4=S3+ b2 (g2)3=13+1∙33=13+27=40
или S4=S3+b4=S3+ b2 (g2)3=13+1∙33=13+27=40
Ответ: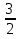 или 40. Вариант ответа указан неправильно: А) Код правильного ответа: Е)
или 40. Вариант ответа указан неправильно: А) Код правильного ответа: Е)
4. 2007. Сборник тестов по математике. Вариант 1, №15 Запас сена таков, что можно ежедневно выдавать на всех лошадей по 96 кг. В действительности, ежедневную порцию каждой лошади смогли увеличить на 4 кг, так как две лошади были переданы соседнему хозяйству. Сколько лошадей было? A) 10 лошадей. B) 6 лошадей. C) 7 лошадей. D) 9 лошадей. E) 8 лошадей. Решение: Случай 1: можно ежедневно выдавать на всех лошадей по 96 кг на каждую.
Лошадей
Ежедневная порция каждой лошади (кг)
Запас сена (кг)
Было
х
96
96х
Осталось
х-2
100
100(х-2)
96х=100(х-2) 96х=100х - 200 200=100х-96х 200=4х х=50 Ответ: 50 лошадей.
Случай 2: можно ежедневно выдавать на всех лошадей 96 кг.
-
Лошадей
Ежедневная порция каждой лошади (кг)
Было
х
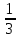
Осталось
х-2
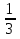
Известно, что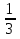 >
> 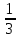 на 4. Отсюда уравнение:
на 4. Отсюда уравнение: 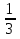 -
- 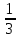 = 4
= 4 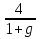 -
- 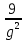 =
= 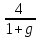
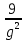 =
= 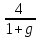 х # 0; 2 96х-96х+192=4х2- 8х 4х2- 8х-192=0 х2- 2х-48=0 D1= (-1)2 -1∙ (-48)=1+48=49>0 х1=
х # 0; 2 96х-96х+192=4х2- 8х 4х2- 8х-192=0 х2- 2х-48=0 D1= (-1)2 -1∙ (-48)=1+48=49>0 х1= 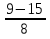 =-6 (не удовлетворяет условию задачи) х2=
=-6 (не удовлетворяет условию задачи) х2= 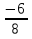 =8 Ответ: 8 лошадей. Некорректное задание. Непонятно: можно ежедневно выдавать на всех лошадей по 96 кг на каждую или можно ежедневно выдавать на всех лошадей 96 кг (если судить по вариантам ответов, то предлог «по» в условии задачи лишний).
=8 Ответ: 8 лошадей. Некорректное задание. Непонятно: можно ежедневно выдавать на всех лошадей по 96 кг на каждую или можно ежедневно выдавать на всех лошадей 96 кг (если судить по вариантам ответов, то предлог «по» в условии задачи лишний).
Правильный ответ: 50 лошадей или 8 лошадей.
10