Рабочая программа по математике 6 класс, Виленкин (ФГОС)

Муниципальное бюджетное образовательное учреждение

Голынковская средняя общеобразовательная школа

Рассмотрено на заседании МО

Протокол № ____

от «____»___________201__ г.

Руководитель МО________

Согласовано Утверждаю

Зам.директора по УВР Директор школы

_________ Т.А.Кирпичникова ________ Г.А.Тимофеева

«___»____________ 201_ г. Приказ № _____ от ____________

Рабочая программа

по математике

для обучающихся 6 класса

Рабочая программа составлена

учителем математики

высшей квалификационной категории

Кругликовой Ириной Ивановной

2014/2015 учебный год

Рабочая программа по математике для 6 класса

составлена на основе нормативных документов:

• Фундаментального ядра содержания общего образования и Требований к результатам освоения основной общеобразовательной программы основного общего образования, представленных в Федеральном государственном образовательном стандарте общего образования;

• Федерального государственного общеобразовательного стандарта основного общего образования;

• Примерной основной образовательной программы образовательного учреждения. Основная школа. Серия: М: . 2011.

• Математика. Сборник рабочих программ. 5 - 6 классы: пособие для учителей общеобразоват. организаций/ [сост. Т.А. Бурмистрова]. - 4-е изд. - М.: Просвещение, 2015 - 80с

• Федерального перечня учебников, рекомендованных Министерством образования Российской Федерации к использованию в образовательном процессе в общеобразовательных учреждениях на 2014/2015 учебный год,

• базисного учебного плана на 2014/2015 учебный года;

• с учетом требований к оснащению образовательного процесса в соответствии с содержанием наполнения учебных предметов компонента государственного стандарта общего образования.

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

Класс 6

Учитель Кругликова Ирина Ивановна

Количество часов:

всего - 170 часов

в неделю - 5 часов

Плановых контрольных работ - 15 ч.

Административных контрольных работ - ___ ч.

Учебники:

1) Математика. 6 класс: учеб. для общеобразоват. учреждений/ Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С И. Шварцбурд. 30-е изд., стер. - М.: Мнемозина, 2013.

Дополнительная литература:

1) Обучение математике в 5 - 6 классах: методическое пособие для учителя к учебнику Н.Я. Виленкина, В.И. Жохова, А.С. Чеснокова, С И. Шварцбурда, - М.: 2014. - 328 с.

2)Разработки уроков, нормативные и контрольно-методические материалы: Математика. 5-6:Книга для учителя. - М.: ИЛЕКСА, 2007.

3) Дидактические материалы по математике: 6 класс: к учебнику Н.Я. Виленкина и др. «Математика. 6 класс» / М.А. Попов - М.: Издательство «Экзамен». 2013.

4) Тесты по математике: 6 класс: к учебнику Н.Я. Виленкина и др. «Математика. 6 класс» / В.Н. Рудницкая. - 2-е изд., перераб. и доп. - М.: Издательство «Экзамен». 2013.

5) Рабочая тетрадь по математике: 6 класс: к учебнику Н.Я. Виленкина и др. «Математика. 6 класс» / Т.М. Ерина. - 6-е изд., перераб. и доп. - М.: Издательство «Экзамен». 2013.

6) Готовимся к ГИА. Математика. 6 класс. Итоговое тестирование в форме экзамена / авт.-сост. Л.П. Донец. - Ярославль: Академия развития; Владимир: ВКТ, 2011.

7) Контрольно-измерительные материалы. Математика. 6 класса / сост. Л.П. Попов. - 2-е изд., перераб. - М.: ВАКО, 2013.

8) Дидактические материалы по математике для 6 класса/А.С. Чесноков, К.И. Нешков - М.: Классикс Стиль, 2007.

Современное математическое образование в системе общего среднего образования занимает одно из ведущих мест, что определяется безусловной практической значимостью математики, ее возможностями в развитии и формировании мышления человека, ее вкладом в создание представлений о научных методах познания действительности. Без математической подготовки невозможно достичь высокого уровня образования необходимого для освоения многих специальностей (экономика, бизнес, финансы, физика, химия, техника и др.), поэтому для большинства школьников математика становится профессионально значимым предметом.

Значимость математики как одного из основных компонентов базового образования определяется ее ролью в научно-техническом прогрессе, в современной науке и производстве, а также важностью математического образования для формирования духовной среды подрастающего человека, его интеллектуальных и морально-этических качеств через овладение обучающимися конкретными математическими знаниями, необходимыми для применения в практической деятельности, достаточными для изучения других дисциплин, для продолжения обучения в системе непрерывного образования.

Новая парадигма образования, реализуемая ФГОС, - это переход от школы информационно-трансляционной к школе деятельностной, формирующей у обучающихся универсальные учебные действия, необходимые для решения конкретных личностно значимых задач. Поэтому изучение математики на ступени основного общего образования направлено на достижение следующих целей:

1. в направлении личностного развития:

• формирование представлений о математике как части общечеловеческой культуры, о значимости математики в развитии цивилизации и современного общества;

• развитие логического и критического мышления, культуры речи, способности к умственному эксперименту;

• формирование интеллектуальной честности и объективности, способности к преодолению мыслительных стереотипов, вытекающих из обыденного опыта;

• воспитание качеств личности, обеспечивающих социальную мобильность, способность принимать самостоятельные решения;

• формирование качеств мышления, необходимых для адаптации в современном информационном обществе;

• развитие интереса к математическому творчеству и математических способностей;

2. в метапредметном направлении:

• развитие представлений о математике как форме описания и методе познания действительности, создание условий для приобретения первоначального опыта математического моделирования;

• формирование общих способов интеллектуальной деятельности характерных для математики и являющихся основой познавательной культуры, значимой для различных сфер человеческой деятельности;

3. в предметном направлении:

• овладение математическими знаниями и умениями, необходимыми для продолжения образования, изучения смежных дисциплин, применения в повседневной жизни;

• создание фундамента для математического развития, формирования механизмов мышления, характерных для математической деятельности.

Данные цели достигаются через интеграцию курса математики с междисциплинарными учебными программами - «Формирование универсальных учебных действий», «Формирование ИКТ- компетентности обучающихся», «Основы учебно-исследовательской и проектной деятельности» и «Основы смыслового чтения и работа с текстом» (см. «Примерная основная образовательная программа образовательного учреждения. Основная школа» - «…программа формирования планируемых результатов освоения междисциплинарных программ предполагает адаптацию итоговых планируемых результатов к возможностям каждого педагога с отражением вклада отдельных предметов…»)

Изучение учебного предмета «Математика» направлено на решение следующих задач:

• формирование вычислительной культуры и практических навыков вычислений;

• формирование универсальных учебных действий, ИКТ-компетентности, основ учебно-исследовательской и проектной деятельности, умений работы с текстом;

• овладение формально-оперативным алгебраическим аппаратом и умением применять его к решению математических и нематематических задач; изучение свойств и графиков элементарных функций, использование функционально-графических представлений для описания и анализа реальных зависимостей;

• ознакомление с основными способами представления и анализа статистических данных, со статистическими закономерностями в реальном мире, приобретение элементарных вероятностных представлений;

• освоение основных фактов и методов планиметрии, формирование пространственных представлений;

• интеллектуальное развитие учащихся, формирование качеств мышления, характерных для математической деятельности и необходимых человеку для полноценного функционирования в обществе;

• развитие логического мышления и речевых умений: умения логически обосновывать суждения, проводить несложные систематизации, приводить примеры и контрпримеры, использовать различные языки математики (словесный, символический, графический);

• формирование представлений об идеях и методах математики как научной теории, о месте математики в системе наук, о математике как форме описания и методе познания действительности;

• развитие представлений о математике как части общечеловеческой культуры, воспитание понимания значимости математики для общественного прогресса.

Содержание математического образования в основной школе включает следующие разделы: арифметика; алгебра; функции, вероятность и статистика, геометрия. Наряду с этим в него включены два дополнительных раздела: логика и множества, математика в историческом развитии, что связано с реализацией целей общеинтеллектуального и общекультурного развития учащихся. Содержание каждого из этих разделов разворачивается в содержательно-методическую линию, пронизывающую все основные разделы содержания математического образования на данной ступени обучения.

Содержание линии «Арифметика» служит фундаментом для дальнейшего изучения учащимся математики и смежных дисциплин, способствует развитию не только вычислительных навыков, но и логического мышления, формированию умения пользоваться алгоритмами, способствует развитию умений планировать и осуществлять деятельность, направленную на решение различных задач, а также приобретению практических навыков, необходимых в повседневной жизни.

Содержание линии «Элементы алгебры» систематизирует знания о математическом языке, показывая применение букв для обозначения чисел и записи свойств арифметических действий, а также для нахождения неизвестных компонентов арифметических действий.

Содержание линии «Наглядная геометрия» способствует формированию у учащихся первичных представлений о геометрических абстракциях реального мира, закладывает основы правильной геометрической речи, развивает образное мышление и пространственные представления.

Линия «Вероятность и статистика» - обязательный компонент школьного образования, усиливающий его прикладное и практическое значение. Этот материал необходим, прежде всего, для формирования у учащегося функциональной грамотности - умения воспринимать и критически анализировать информацию, представленную в различных формах, понимать вероятностный характер многих реальных зависимостей, производить простейшие вероятностные расчеты. Изучение основ комбинаторики позволит учащимся осуществлять рассмотрение случаев, перебор и подсчет числа вариантов, в том числе в простейших прикладных заданиях. При изучении статистики и вероятности обогащаются представления о современной картине мира и методах его исследования, формируется понимание роли статистики как источника социально значимой информации, закладываются основы вероятностного мышления.

Программа составлена с учетом принципа преемственности между основными ступенями обучения: начальной, основной и полной средней школой.

Результаты изучения предмета «Математика» в 6 классе представлены на нескольких уровнях - личностном, метапредметном и предметном.

Личностные:

1. ответственное отношение к учению, готовность и способность обучающихся к саморазвитию и самообразованию на основе мотивации к обучению и познанию;

2. первичная сформированность коммуникативной компетентности в общении и сотрудничестве со сверстниками, старшими и младшими в образовательной, учебно-исследовательской, творческой и других видах деятельности;

3. умение ясно, точно, грамотно излагать свои мысли в устной и письменной речи, понимать смысл поставленной задачи, выстраивать аргументацию, приводить примеры и контрпримеры;

4. первоначальное представление о математической науке как сфере человеческой деятельности, об этапах её развития значимости для развития цивилизации;

5. критичность мышления, умение распознавать логически некорректные высказывания, отличать гипотезу от факта;

6. креативность мышления, инициативы, находчивости, активность при решении арифметических задач;

7. умение контролировать процесс и результат учебной математической деятельности;

8. формирование способности к эмоциональному восприятию математических объектов, задач, решений, рассуждений;

Метапредметные:

1. способность самостоятельно планировать альтернативные пути достижения целей, осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач;

2. умение осуществлять контроль по образцу и вносить необходимые коррективы;

3. способность адекватно оценивать правильность или ошибочность выполнения учебной задачи, её объективную трудность и собственные возможности её решения;

4. умение устанавливать причинно-следственные связи; строить логические рассуждения, умозаключения (индуктивные, дедуктивные и по аналогии) и выводы;

5. умение создавать, применять и преобразовывать знаково-символические средства, модели и схемы для решения учебных и познавательных задач;

6. развитие способности организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками: определять цели, распределять функции и роли участников, взаимодействовать и находить общие способы работы; умения работать в группе: находить общее решение и разрешать конфликты на основе согласования позиций и учёта интересов; слушать партнёра; формулировать, аргументировать и отстаивать своё мнение;

7. формирование учебной и обще пользовательской компетентности в области использования информационно-коммуникационных технологий (ИКТ-компетентности);

8. первоначального представление об идеях и о методах математики как об универсальном языке науки и техники;

9. развитие способности видеть математическую задачу в других дисциплинах, в окружающей жизни;

10. умение находить в различных источниках информацию, необходимую для решения математических проблем, и представлять её в понятной форме; принимать решение в условиях неполной и избыточной, точной и вероятностной информации;

11. умение понимать и использовать математические средства наглядности (рисунки, чертежи, схемы и др.) для иллюстрации, интерпретации, аргументации;

12. умение выдвигать гипотезы при решении учебных задач и понимания необходимости их проверки;

13. понимание сущности алгоритмических предписаний и умения действовать в соответствии с предложенным алгоритмом;

14. умения самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем;

15. способность планировать и осуществлять деятельность, направленную на решение задач исследовательского характера.

Предметные:

1. умения работать с математическим текстом (структурирование, извлечение необходимой информации), точно и грамотно выражать свои мысли в устной и письменной речи, применяя математическую терминологию и символику, использовать различные языки математики (словесный, символический, графический), развития способности обосновывать суждения, проводить классификацию;

2. владения базовым понятийным аппаратом: иметь представление о числе, дроби, процентах, об основных геометрических объектах (точка, прямая, ломаная, угол, многоугольник, многогранник, круг, окружность, шар, сфера и пр.), формирования представлений о статистических закономерностях в реальном мире и различных способах их изучения;

3. умения выполнять арифметические преобразования рациональных выражений, применять их для решения учебных математических задач и задач, возникающих в смежных учебных предметах;

4. умения пользоваться изученными математическими формулами;

5. знания основных способов представления и анализа статистических данных; умения решать задачи с помощью перебора всех возможных вариантов;

6. умения применять изученные понятия, результаты и методы при решении задач из различных разделов курса, в том числе задач, не сводящихся к непосредственному применению известных алгоритмов.

В результате изучения математик в 5-6 классах

Рациональные числа

Ученик научится:

• понимать особенности десятичной системы счисления;

• владеть понятиями, связанными с делимостью натуральных чисел;

• выражать числа в эквивалентных формах, выбирая наиболее подходящую в зависимости от конкретной ситуации;

• сравнивать и упорядочивать рациональные числа;

• выполнять вычисления с рациональными числами, сочетая устные и письменные приёмы вычислений, применение калькулятора;

• использовать понятия и умения, связанные с пропорциональностью величин, процентами в ходе решения математических задач и задач из смежных предметов, выполнять несложные практические расчёты.

Ученик получит возможность:

• познакомиться с позиционными системами счисления с основаниями, отличными от 10;

• углубить и развить представления о натуральных числах и свойствах делимости;

• научиться использовать приемы, рационализирующие вычисления, приобрести привычку контролировать вычисления, выбирая подходящий для ситуации способ.

Действительные числа

Ученик получит возможность:

• развить представление о числе и числовых системах от натуральных до действительных чисел; о роли вычислений в человеческой практике;

• развить и углубить знания о десятичной записи рациональных чисел.

Измерения, приближения, оценки

Ученик научится:

• использовать в ходе решения задач элементарные представления, связанные с приближёнными значениями величин.

Ученик получит возможность:

• понять, что числовые данные, которые используются для характеристики объектов окружающего мира, являются преимущественно приближенными;

• понять, что погрешность результата вычислений должна быть соизмерима с погрешностью исходных данных.

Наглядная геометрия

Ученик научится:

• распознавать на чертежах, рисунках, моделях и в окружающем мире плоские и пространственные геометрические фигуры;

• распознавать развёртки куба, прямоугольного параллелепипеда, правильной пирамиды, цилиндра и конуса;

• строить развёртки куба и прямоугольного параллелепипеда;

• определять по линейным размерам развертки фигуры линейные размеры самой фигуры и наоборот;

• вычислять объём прямоугольного параллелепипеда.

Ученик получит возможность:

• вычислять объемы пространственных геометрических фигур, составленных из прямоугольных параллелепипедов;

• углубить и развить представления о пространственных геометрических фигурах;

• применять понятие развертки для выполнения практических расчетов.

Базисный учебный план образовательных учреждений Российской Федерации, реализующих основную образовательную программу основного общего образования предусматривает обязательное изучение математики в 6 классе в объеме 170 часов (5 часов в неделю).

СОДЕРЖАНИЕ КУРСА

Делимость чисел (20 ч)

Делители и кратные. Признаки делимости на 2, 3, 5, 9, 10. Простые и составные числа. Разложение натурального числа на простые множители. Наибольший общий делитель. Взаимно простые числа. Наименьшее общее кратное.

Сложение и вычитание дробей с разными знаменателями (22ч)

Основное свойства дробим. Сокращение дробей. Приведение дробей к общему знаменателю. Сравнение, сложение и вычитание дробей с разными знаменателями. Сложение и вычитание смешанных чисел.

Умножение и деление обыкновенных дробей (32 ч)

Умножение дробей. Нахождение дроби от числа. Применение распределительного свойства умножения. Взаимно обратные числа. Деление. Нахождение числа по его дроби. Дробные выражения.

Отношения и пропорции (19 ч)

Отношения. Пропорции. Прямая и обратная пропорциональные зависимости. Масштаб. Длина окружности. Площадь круга. Шар.

Положительные и отрицательные числа (13 ч)

Координаты на прямой. Противоположные числа. Модуль числа. Сравнение чисел. Изменение величин.

Сложение и вычитание положительных и отрицательных чисел (11 ч)

Сложение чисел с помощью координатной прямой. Сложение отрицательных чисел. Сложение чисел с разными знаками. Вычитание.

Умножение и деление положительных и отрицательных чисел (12 ч)

Умножение. Деление. Рациональные числа. Свойства действий с рациональными числами.

Решение уравнений (13 ч)

Раскрытие скобок. Коэффициент. Подобные слагаемые. Решение уравнений.

Координаты на плоскости (13 ч)

Перпендикулярные прямые. Параллельные прямые. Координатная плоскость. Столбчатые диаграммы. Графики.

Повторение. Решение задач (13 ч)

Систематизация и обобщение курса математики 5 - 6 классов.

Для оценки достижений обучающегося используются следующие виды и формы контроля:

• Система контрольных работ

  • Контрольная работа проверочная

  • Тест

  • ТДР

  • Зачет

  • Диктант

  • Взаимоконтроль

  • Самоконтроль

• Диагностика уровней сформированности компонентов учебной деятельности (Г. В. Репкина, Е.В. Заика)

Реализация рабочей программы осуществляется в следующих видах деятельности школьника:

1. Индивидуальная - выполнение учебных заданий каждым учеником самостоятельно на уровне его способностей и возможностей.

2. Групповая - в процессе её предполагается сотрудничество нескольких человек, перед ними ставится конкретная учебно-познавательная задача.

3. Парная - когда учебная задача выполняется усилиями пары.

4. Фронтальная - одновременное участие всех обучаемых в общей для всех учебной деятельности под руководством учителя.

КРИТЕРИИ И НОРМЫ ОЦЕНКИ ЗУН ОБУЧАЮЩИХСЯ

Единые нормы являются основой при оценке как контрольных, так и всех других письменных работ по математике. Они обеспечивают единство требований к обучающимся со стороны всех учителей образовательного учреждения, сравнимость результатов обучения в разных классах. Применяя эти нормы, учитель должен индивидуально подходить к оценке каждой письменной работы обучающегося, обращая внимание на качество выполнения работы в целом, имеющиеся достижения обучающегося, а затем уже на количество ошибок и на их характер. Приведенные ниже рекомендации - примерные, указанное число и характер ошибок находятся в соответствии с требованиями к каждому из уровней достижений, описанных в Примерной образовательной программе.

Содержание и объем материала, включаемого в контрольные письменные работы, а также в задания для повседневных письменных упражнений, определяются требованиями, установленными образовательной программой. Наряду с контрольными работами по отдельным разделам темы следует проводить итоговые контрольные работы по всей изученной теме.

По характеру заданий письменные работы могут состоять: а) только из примеров; б) только из задач; в) из задач и примеров.

Контрольные работы, которые имеют целью проверку достижения предметных результатов обучающихся по целому разделу программы, а также по материалу, изученному за четверть (триместр) или за год, как правило, должны состоять из задач и примеров.

Оценка письменной работы определяется с учетом прежде всего ее общего математического уровня, оригинальности, последовательности, логичности ее выполнения, а также числа ошибок и недочетов и качества оформления работы.

Ошибка, повторяющаяся в одной работе несколько раз, рассматривается как одна ошибка.

За орфографические ошибки, допущенные обучающимися, оценка не снижается; об орфографических ошибках доводится до сведения преподавателя русского языка. Однако ошибки в написании математических терминов, уже встречавшихся обучающимся, должны учитываться как недочеты в работе.

При оценке письменных работ по математике различают грубые ошибки, ошибки и недочеты.

Грубыми в 5 - 6 классах считаются ошибки, связанные с вопросами, включенными в «Требования к уровню подготовки оканчивающих начальную школу» образовательных стандартов, а также показывающие, что обучающийся не усвоил вопросы изученных новых тем, отнесенные стандартами основного общего образования к числу обязательных для усвоения всеми обучающимися.

Так, например, к грубым относятся ошибки в вычислениях, свидетельствующие о незнании таблицы сложения или таблицы умножения, связанные с незнанием алгоритма письменного сложения и вычитания, умножения и деления на одно- или двухзначное число и т.п., ошибки, свидетельствующие о незнании основных формул, правил и явном неумении их применять, о незнании приемов решения задач, аналогичных ранее изученным.

Примечание. Если грубая ошибка встречается в работе только в одном случае из нескольких аналогичных, то при оценке работы эта ошибка может быть приравнена к негрубой.

Примерами негрубых ошибок являются: ошибки, связанные с недостаточно полным усвоением текущего учебного материала, не вполне точно сформулированный вопрос или пояснение при решении задач, неточности при выполнении геометрических построений и т.п.

Недочетами считаются нерациональные записи при вычислениях, нерациональные приемы вычислений, преобразований и решений задач, небрежное выполнение чертежей и схем, отдельные погрешности в формулировке пояснения или ответа к задаче. К недочетам можно отнести и другие недостатки работы, вызванные недостаточным вниманием обучающихся, например: неполное сокращение дробей или членов отношения; обращение смешанных чисел в неправильную дробь при сложении и вычитании; пропуск наименований; пропуск чисел в промежуточных записях; перестановка цифр при записи чисел; ошибки, допущенные при переписывании т.п.

Оценка письменной работы по выполнению вычислительных

заданий и алгебраических преобразований

Оценка «5» ставится за безукоризненное выполнение письменной работы, т.е.

а) если решение всех примеров верное;

б) если все действия и преобразования выполнены правильно, без ошибок; все записи хода решения расположены последовательно, а также сделана проверка решения в тех случаях, когда это требуется.

Оценка «4» ставится за работу, которая выполнена в основном правильно, но допущена одна (негрубая) ошибка или два-три недочета.

Оценка «3» ставится в следующих случаях:

а) если в работе имеется одна грубая ошибка и не более одной негрубой ошибки;

б) при наличии одной грубой ошибки и одного-двух недочетов;

в) при отсутствии грубых ошибок, но при наличии от двух до четырех (негрубых) ошибок;

г) при наличии двух негрубых ошибок и не более трех недочетов;

д) при отсутствии ошибок, но при наличии четырех и более недочетов;

е) если верно выполнено более половины объема всей работы.

Оценка «2» ставится, когда число ошибок превосходит норму, при которой может быть выставлена положительная оценка, или если правильно выполнено менее половины всей работы.

Оценка «1» ставится, если обучающийся совсем не выполнил работу.

Примечание. Оценка «5» может быть поставлена, несмотря на наличие одного-двух недочетов, если обучающийся дал оригинальное решение заданий, свидетельствующее о его хорошем математическом развитии.

Оценка письменной работы по решению текстовых задач

Оценка «5» ставится в том случае, когда задача решена правильно: ход решения задачи верен, все действия и преобразования выполнены верно и рационально; в задаче, решаемой с вопросами или пояснениями к действиям, даны точные и правильные формулировки; в задаче, решаемой с помощью уравнения, даны необходимые пояснения; записи правильны, расположены последовательно, дан верный и исчерпывающий ответ на вопросы задачи; сделана проверка решения (в тех случаях, когда это требуется).

Оценка «4» ставится в том случае, если при правильном ходе решения допущена одна негрубая ошибка или два-три недочета.

Оценка «3» ставится в том случае, если ход решения правильный, но:

а) допущена одна грубая ошибка и не более одной негрубой ошибки;

б) допущена одна грубая ошибка и не более двух недочетов;

в) допущены три-четыре негрубые ошибки при отсутствии недочетов;

г) допущено не более двух негрубых ошибок и трех недочетов;

д) при отсутствии ошибок, но при наличии более трех недочетов.

Оценка «2» ставится в тои случае, когда число ошибок превосходит норму, при которой может быть выставлена положительная оценка.

Оценка «1» ставится в том случае, если обучающийся не выполнил ни одного задания работы.

Примечание.

1. 1. Оценка «5» может быть поставлена, несмотря на наличие описки или недочета, если обучающийся дал оригинальное решение, свидетельствующее о его хорошем математическом развитии.

   2. Положительная оценка «3» может быть выставлена обучающемуся, выполнившему работу не полностью, если он безошибочно выполнил более половины объема всей работы.

Оценка комбинированных письменных работ по математике

Письменная работа по математике, подлежащая оцениванию, может состоять из задач и примеров (комбинированная работа). В этом случае преподаватель сначала дает предварительную оценку каждой части работы, а затем общую, руководствуясь следующим;

а) если обе части работы оценены одинаково, то эта оценка должна быть общей для всей работы в целом;

б) если оценки частей разнятся на один балл, например, даны оценки «5» и «4» или «4» и «3» и т.п., то за работу в целом, как правило, ставится низшая из двух оценок, но при этом учитывается значение каждой из частей работы;

в) низшая из двух данных оценок ставится и в том случае, если одна часть работы оценена баллом «5», а другая - баллом «3», но в этом случае преподаватель может оценить такую работу в целом баллом «4» при условии, что оценка «5» поставлена за основную часть работы;

г) если одна из двух частей работы оценена баллом «5» или «4», а другая - баллом «2» или «1», то за всю работу в целом ставится балл «2», но преподаватель может оценить всю работу баллом «3» при условии, что высшая из двух данных оценок поставлена за основную часть работы.

Примечание. Основной считается та часть работы, которая включает больший по объему или наиболее важный по значению материал по изучаемым темам программы.

Оценка текущих письменных работ

При оценке повседневных обучающих работ по математике учитель руководствуется указанными нормами оценок, но учитывает степень самостоятельности выполнения работ обучающимися, а также то, насколько закреплен вновь изучаемый материал.

Обучающие письменные работы, выполненные обучающимися вполне самостоятельно с применением ранее изученных и хорошо закрепленных знаний, оцениваются так же, как и контрольные работы.

Обучающие письменные работы, выполненные вполне самостоятельно, на только что изученные и недостаточно закрепленные правила, могут оцениваться на один балл выше, чем контрольные работы, но оценка «5» и в этом случае выставляется только за безукоризненно выполненные работы.

Письменные работы, выполненные в классе с предварительным разбором их под руководством учителя, оцениваются на один балл ниже, чем это предусмотрено нормами оценки контрольных письменных работ. Но безукоризненно выполненная работа и в этом случае оценивается баллом «5».

Домашние письменные работы оцениваются так же, как классная работа обучающего характера.

Оценка устных ответов обучающихся

Ответ оценивается отметкой «5», если обучающийся:

- полно раскрыл содержание материала в объеме, предусмотренном программой и учебником;

- изложил материал грамотным языком, точно используя математическую терминологию и символику, в определенной логической последовательности;

- правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;

- показал умение иллюстрировать теорию конкретными примерами, применять ее в новой ситуации при выполнении практического задания;

- продемонстрировал усвоение ранее изученных сопутствующих вопросов, сформированность и устойчивость используемых при ответе умений и навыков;

- отвечал самостоятельно, без наводящих вопросов учителя;

- возможны одна-две неточности при освещении второстепенных вопросов или в выкладках, которые обучающие легко исправил после замечания учителя.

Ответ оценивается отметкой «4», если удовлетворяет в основном, требованиям на оценку «5», но при этом имеет один из недостатков:

- в изложении допущены небольшие пробелы, не исказившие математическое содержание ответа;

- допущены один-два недочетов при освещении основного содержании ответа, исправленные после замечания учителя;

- допущены ошибка или более двух недочетов при освещении второстепенных вопросов или в выкладках, легко исправленные после замечания учителя.

Отметка «3» ставится в следующих случаях:

- неполно раскрыто содержание материала (содержание изложено элементарно, не всегда последовательно), но показано общее понимание вопроса и продемонстрированы умения, недостаточные для дальнейшего усвоения программного материала (определенные «Требованиями к математической подготовки учащихся» в настоящей программе по математике);

- имелись затруднения или допущены ошибки в определении понятий, использовании математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов учителя;

- ученик не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме;

- при достаточном знании теоретического материала выявлена недостаточная сформированность основных умений и навыков.

Отметка «2» ставится в следующих случаях:

- не раскрыто основное содержание учебного материала;

- обнаружено незнание или непонимание обучающимся, большей или наиболее важной части учебного материала;

- допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках в выкладках, которые не исправлены после нескольких наводящих вопросов учителя.

Отметка «1» ставится если:

- обучающийся обнаружил полное незнание и непонимание изучаемого материала или не смог ответить ни на один из поставленных вопросов по изучаемому материалу.

Общая классификация ошибок.

При оценке знаний, умений и навыков обучающихся следует учитывать все ошибки (грубые и негрубые) и недочёты.

Грубыми считаются ошибки:

-незнание определения основных понятий, законов, правил, основных положений теории, незнание формул, общепринятых символов обозначений величин, единиц их измерения;

-незнание наименований единиц измерения;

-неумение выделить в ответе главное;

-неумение применять знания, алгоритмы для решения задач;

-неумение делать выводы и обобщения;

-неумение читать и строить графики;

-неумение пользоваться первоисточниками, учебником и справочниками;

-потеря корня или сохранение постороннего корня;

-отбрасывание без объяснений одного из них;

-равнозначные им ошибки;

-вычислительные ошибки, если они не являются опиской;

-логические ошибки.

К негрубым ошибкам следует отнести:

-неточность формулировок, определений, понятий, теорий, вызванная неполнотой охвата основных признаков определяемого понятия или заменой одного - двух из этих признаков второстепенными;

-неточность графика;

-нерациональный метод решения задачи или недостаточно продуманный план ответа (нарушение логики, подмена отдельных основных вопросов второстепенными);

-нерациональные методы работы со справочной и другой литературой;

-неумение решать задачи, выполнять задания в общем виде.

Недочетами являются:

-нерациональные приемы вычислений и преобразований;

-небрежное выполнение записей, чертежей, схем, графиков.

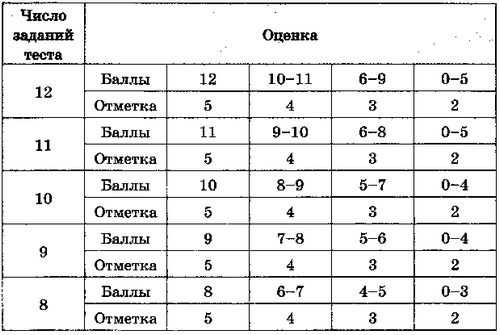
Оценка тестовых работ обучающихся

Промежуточная аттестация: итоговая оценка

за четверть (триместр) и за год

В соответствии с особенностями математики как учебного предмета оценки за письменные работы имеют большее значение, чем оценки за устные ответы и другие виды работ.

Поэтому при выведении итоговой оценки за четверть (триместр) «среднеарифметический подход» недопустим - такая оценка не отражает достаточно объективно уровень подготовки и математического развития обучающегося. Итоговую оценку определяют в первую очередь оценки за контрольные работы, затем принимаются во внимание оценки за другие письменные и практические работы и лишь в последнюю очередь - все прочие оценки (за устные ответы, устный счет и т.д.). При этом учитель должен учитывать и фактически уровень знаний и умений обучающегося на конец четверти (триместра).

Итоговая оценка за год выставляется на основании четвертных (триместровых) оценок, но также с обязательным учетом фактического уровня знаний обучающегося на конец учебного года.

Календарно - тематическое планирование курса математики 6 класса