Конспект занятия факультатива по математике Решение текстовых задач арифметическим способом с помощью смешанных дробей (6 класс)

Занятие факультатива в 6 классе по теме: «Решение текстовых задач арифметическим способом с помощью смешанных дробей».

Цели занятия: образовательная - систематизировать и обобщить знания, умения и навыки по решению задач разных типов;

развивающая - способствовать формированию умений применять полученные знания, развивать логическое мышление, внимание, память, творческие навыки, активизировать познавательную деятельность;

воспитательная - содействовать воспитанию интереса к математике, творческой активности; повысить культуру поведения, культуру речи, умения общаться.

Оборудование:

проектор, компьютер, компьютерная презентация.

Ход занятия.

Сегодня на занятии мы вспомним задачи различных типов и решим их, оформив различными способами.

Давайте вспомним какие типы задач мы ре­шали:

• на части;

• на движение;

• на работу;

• на предположение и т. д.

Какие способы оформления задач мы знаем:

• пояснением;

• с вопросами;

• числовым выражением.

Задача №1 и мы решим ее устно:

У Пети и Коли вместе 27 яблок. Известно, что у Коли на 5 яблок меньше. Сколько яблок у Коли и Пети?

Какого типа эта задача? (на предположение)

• Что нам известно? (у Пети и Коли 27 яблок)

• Что это значит? (всего 27 яблок)

• Что еще известно? (у Коли на 5 яблок меньше)

• Как найти сколько яблок у Коли?

1) 27 - 5 = 22 удвоенное число яблок у Коли.

2) 22 : 2 = 11 яблок у Коли.

3) 11 + 5 = 16 яблок у Пети.

Ответ: 11яблок у Коли и 16 яблок у Пети.

Задача №2. Решим её письменно.

Цистерна с бензином весит 900кг, причем масса бензина на

100 кг, больше массы цистерны. Какова масса пустой цистерны?

• Что известно? ( масса цистерны с бензином)

• Что это значит? ( масса цистерны и масса бензина вместе)

• Что еще известно? ( масса бензина > массы цистерны)

• Как найти массу пустой цистерны?

Давайте решим эту задачу числовым выражением.

(900-100) : 2 = 400(кг).

Ответ: 400кг масса пустой цистерны.

Задачи №3 и №4.Следующий тип задач. Таблица дана.

1

2

Вместе

3ч

6ч

?

10ч

?

6 ч

Какого типа задачи? (на работу)

Решим эти задачи устно.

3) Через 1 трубу бак можно наполнить за 3 часа, через 2 трубу - за 6 часов. За сколько часов наполнится бака, если открыть две трубы? ( : ( + ) = 1(час))

4) Два трактора вспахали поле за 6 часов. Первый мог бы один вспахать за 10 часов. За сколько часов второй трактор вспашет поля? ( : ( - ) = 5(часов))

Задача №5. Эту задачу мы решим письменно.

Первая бригада может выполнить задание за 9 дней, а вторая - за

12 дней. Первая бригада работала над выполнением этого задания

3 дня, а потом вторая бригада закончила работу. За сколько дней

было выполнено задание?

- Что требуется найти? ( сколько дней работала 2 бригада)

• Кто выполнял это задание? (две бригады вместе)

• Что знаем о 1 бригаде? ( она работала 3 дня)

• А потом кто работал? ( вторая бригада)

• Как найти время работы 2 бригады? ( работу, выполняемую 2 бригадой разделить на ту часть работы, которую она выполняет за 1 день)

• Как найти ту часть работы, которую выполняет 1 бригада?
  
  (всю работу разделить на время выполнения работы 1 бригадой)

- А остальную часть работы выполнила 2 бригада. Какую именно? (из всей работы вычесть часть работы, выполненную 1 бригадой)

Решим эту задачу с вопросами.

Примем всю работу за 1.

1) Какую часть работы выполнила 1 бригада за 1 день?

1:9=

2. Какую часть работы выполнила 2 бригада за 1 день?
   
   1 : 12 =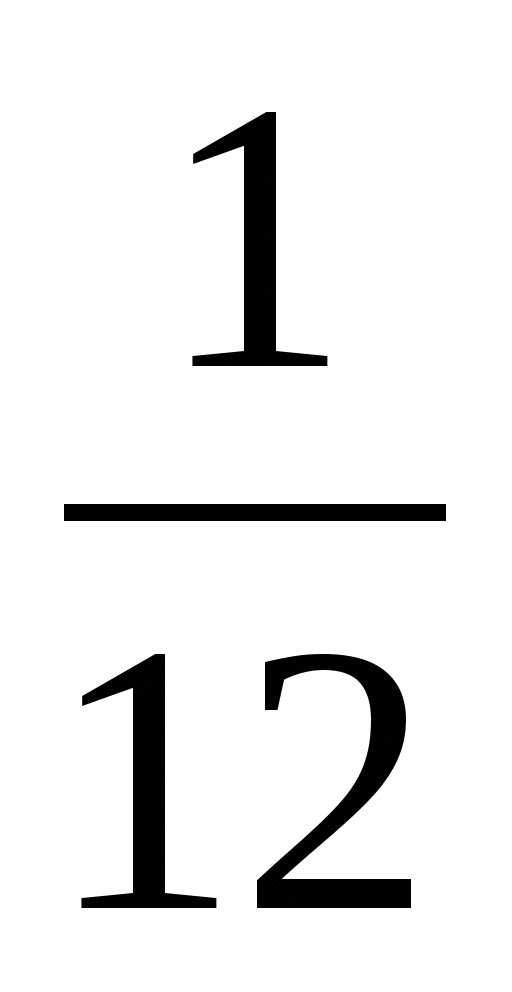

3. Какую часть работы выполнила 1 бригада за 3 дня?
   
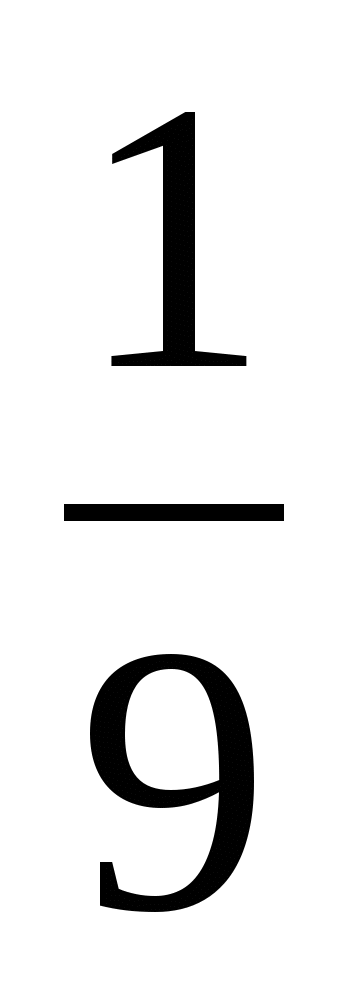   ∙ 3 =

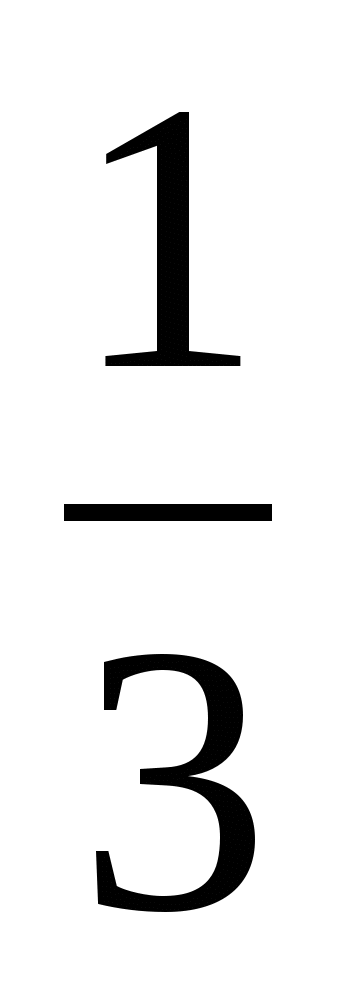
4. Какую часть работы осталось выполнить 2 бригаде?
   
   1 - =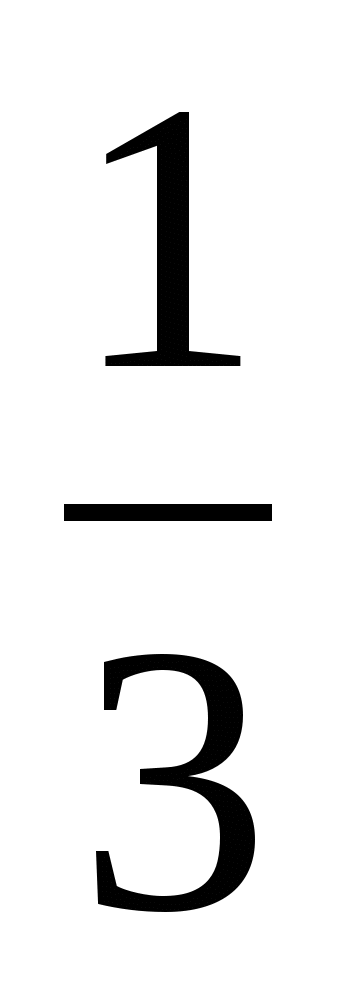

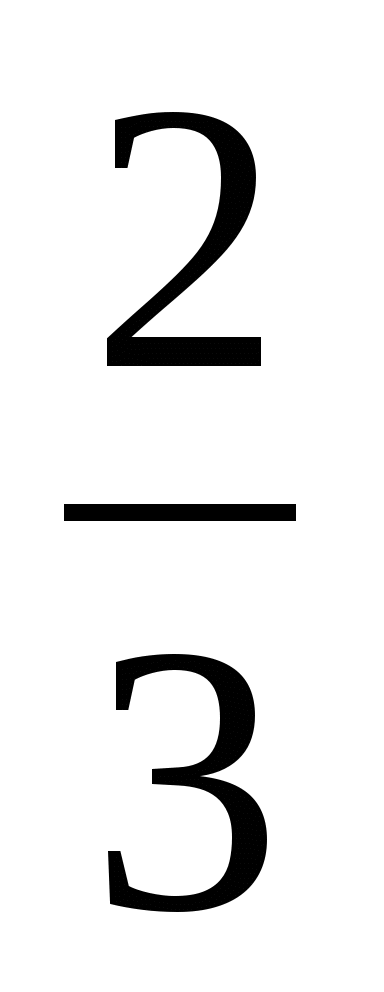
5) Сколько дней работала 2 бригада?

: = ∙ = 8

6) За сколько дней было выполнено задание?

3 + 8 = 11

Ответ: за 11 дней.

Задача № 6.

Моторная лодка проходит расстояние между двумя пунктами А и В за 2 часа по течению реки, а плот за 8 часов. Какое время затратит моторная лодка на обратный путь?

• 
  
  
  
  

  
  
  
  
  Какой тип задачи? (на движение)

• Чем отличается движение по реке от других видов движения? (несколькими скоростями)

- Какие это скорости? ( скорость по течению, скорость против течения, скорость течения, собственная скорость лодки)

- Как связаны между собой скорости?

( Скорость по течению = скорость течения + скорость собственная;

скорость против течения = скорость собственная - скорость течения)

• Чем отличается скорость по течению от скорости против тече­ния? (удвоенной скоростью течения)

Решим эту задачу с пояснением.

1. 1 : 2 = 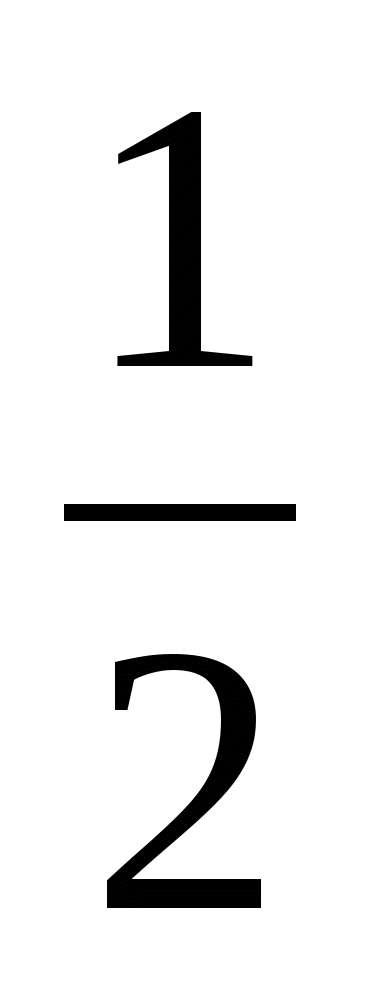(часть) пути - скорость по течению.

2. 1 : 8 = 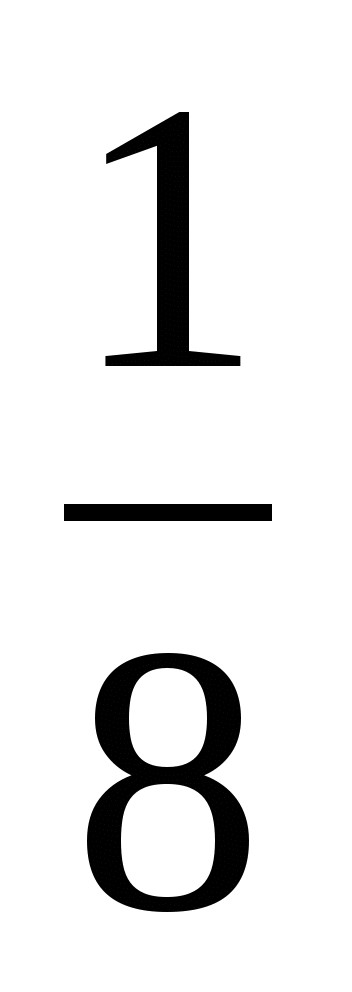(часть) пути - скорость течения.

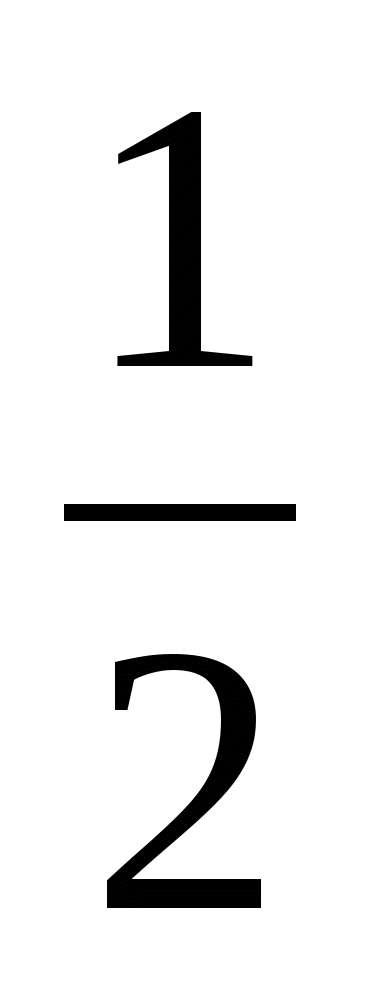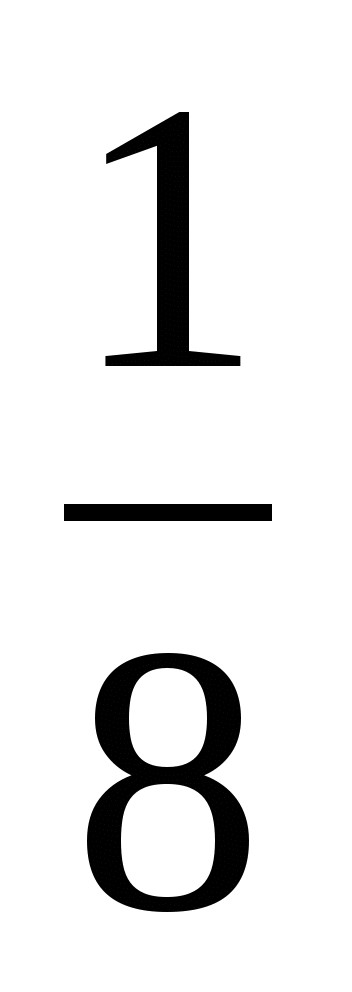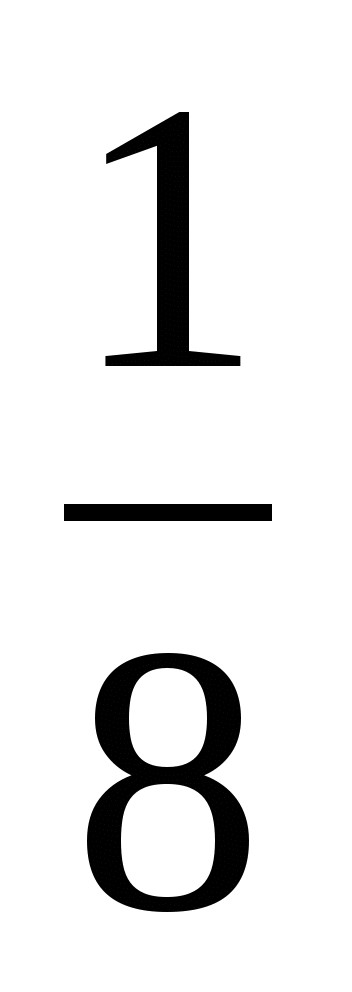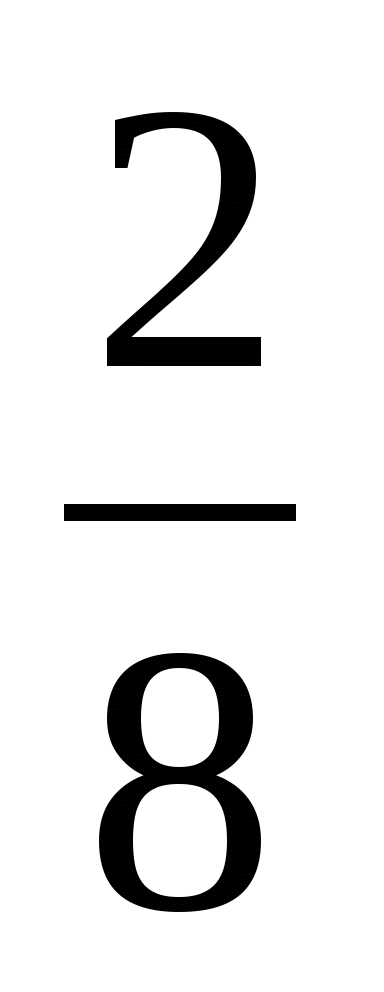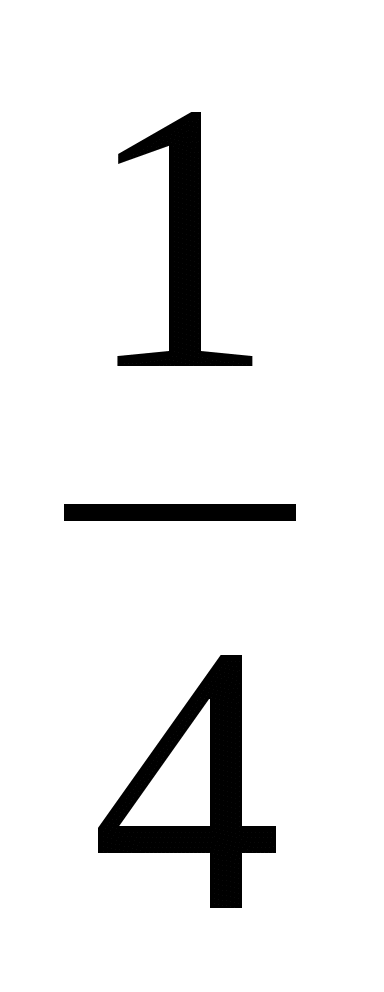3. - - = = (часть) пути - скорость против течения.

4. 1 : 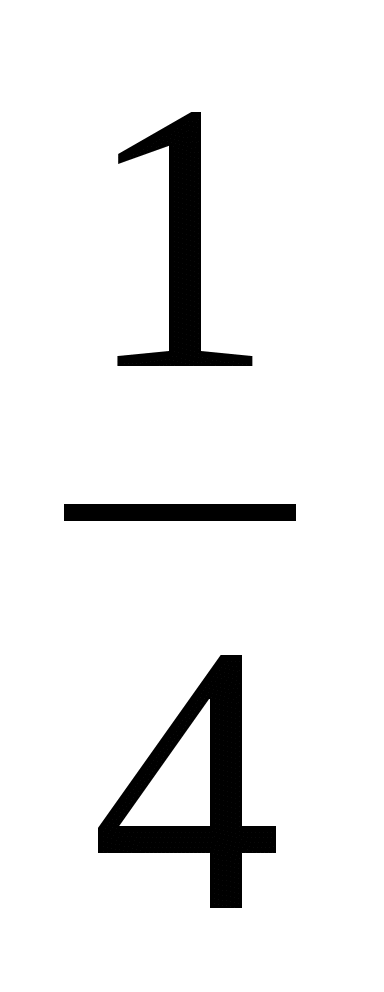= 4 (часа) затратит лодка на обратный путь.
   
   Ответ: 4 часа.

Итак, мы вспомнили три типа задач и способы решения их. Молодцы. Решали очень хорошо.

Домашнее задание: Придумать 2 свои задачи разных типов (записать на карточки)

Занятие окончено. Спасибо.