- Учителю
- Исследовательская работаЕстественные науки в произведениях Льюиса Кэрролла
Исследовательская работаЕстественные науки в произведениях Льюиса Кэрролла

СОДЕРЖАНИЕ
Введение…………………………………………………………………….…………………2
Глава I. Логика Л.Кэрролла……………………………………………………….……….4
Понятие логики…………………………………………………………………………4
История развития логики………………………………………………..…………….5
Символическая логика…..………………………………………………………………7
Символическая логика Льюиса Л.Кэрролла……………….………………………….9
Кэрролловская логика в сказках об Алисе….…………………………………………19
Парадоксы Л.Кэрролла…………………………………………………………………21
Чеширский кот………………………………………………………………………….24
Кэрролловская арифметика в сказках об Алисе…………………………………..…26
Фантазии Л. Кэрролла и информатика………………………………………...……27
Глава II. Геометрия и физика Л. Кэрролла………………………………………………30
Мысли о свободном падении…………………………………………………………...30
Свойства окружности…………………………………………………………………31
Идеализация пространства………………………………………………………...…33
Схематизация времени……………………………………...…………………………34
Зеркальная симметрия…………………………………………………………………36
Математика Зазеркалья ……………………………………………………………...37
Физика Зазеркалья………………………………………………………………………38
Заключение.………………………………………………………………………………..…45
Литература.………………………………………………………………………………...…47
Введение
Сказки об Алисе принадлежит к числу тех сказок, которые встречают нас ещё в детстве и могут сопровождать всю жизнь. Они написаны для детей, но особенно читаемы взрослыми. Что же касается «Алисы», то при внимательном чтении в ней открываются такие глубины, что некоторые, в том числе философ и логик Бертран Рассел, даже предлагают издавать обе сказки Льюиса Кэрролла с грифом «Только для взрослых».
Я перечитывала произведения Л.Кэрролла достаточно часто, находя за словами, складывающимися в причудливые строки, скрытый смысл, высмеивающий слепую веру обыденного человека в незыблемость законов природы. Возвращаясь к произведениям Л.Кэрролла уже во взрослом возрасте, можно подметить многое из того, что проходит мимо в силу недостатка образования и жизненного опыта. Ну а расплодившиеся в последнее время бесчисленные комментарии к этому бессмертному примеру мастерского одурачивания открывают глаза на бесспорную гениальность творческого метода ученого, любившего математику.
При желании, в сказках об Алисе можно обнаружить предпосылки квантовой физики и теории относительности, размышления о неразрешимых в то время парадоксах академической математики, как науки базирующейся на аристотелевской логике, и даже начала неевклидовой геометрии.
И все это сэр Чарльз Доджсон проделывал с неподражаемым изяществом и юмором, вовлекая читателя в бесконечную логико-словесную игру. И эта игра - нравится читателю своей непредсказуемостью.


Илл. Lewis Carroll (1863) из рукописи Фото Кэрролла. Сестры Лидделл.
"Приключения Алисы под землей"
Ошеломленному читателю, впервые открывающему произведения Л.Керрола, может показаться, что все в них спутано, все непонятно и бессмысленно. Однако, вглядевшись, он начинает понимать, что в бессмыслице этой есть своя логика и своя система.
Чувство это крепнет при повторном прочтении, а «Алиса в стране чудес» и «Алиса в Зазеркалье» принадлежат к тем книгам, к которым возвращаешься снова и снова на протяжении всей жизни, каждый раз читая ее новыми глазами. Недаром столько замечательных людей любили эти сказки и писали о ней - Гилберт Честертон, Бертран Рассел, Норберт Винер, выдающиеся физики и математики наших дней. Льюис Кэрролл соединяет несоединимое и с такой же легкостью разъединяет неразрывное.
«Прощайте, ноги!» − говорит Алиса стремительно убегающим от нее ногам. И принимается строить планы, как она будет посылать им подарки к рождеству.
Чеширский Кот обладает чудесной способностью медленно и частями исчезать: медленное исчезновение - разве это понятие не соединяет в себе несоединимое? Все мы знаем котов без улыбки, но вот Л.Кэрролл подарил нам еще и улыбку без кота! Знаменитая улыбка Чеширского Кота одиноко парит в воздухе как символ иронии и отрицания бессмысленного мира, по которому странствует Алиса.
В эпизоде, когда Алиса пытается вспомнить таблицу умножения, она доходит до абсурда, всё перепутав: «Значит, так: четырежды пять - двенадцать, четырежды шесть - тринадцать, четырежды семь… Так я до двадцати никогда не дойду!»
Почему Алиса никогда не дойдет до 20, проще всего объяснить следующим образом: английская таблица умножения традиционно кончается на 12, так что если продолжать эту абсурдную прогрессию - 4∙5=12, 4∙6=13, 4∙7=14 и т.д., − то придется остановиться на 4∙12=19. До 20 не хватит единицы. Вот так: абсурд, если присмотреться, совсем не лишен смысла.
Льюис Кэрролл пользуется славой короля бессмыслицы. Он ее заслужил. «Он не только учил детей стоять на голове, − писал о Кэрролле Честертон. - Он учил ученых стоять на голове». Но было бы неправильно представить себе бессмыслицу как полный хаос и авторский произвол. Вот почему Честертон прибавляет: «Какая же это была голова, если на ней можно было так стоять!»
Изложенное выше, послужило основанием для формулировки темы нашего исследования, цель которого изучение творческого наследия Л.Кэрролла, с точки зрения естественных наук, и прежде всего, математики.
Объектом исследования являются произведения Л.Кэррола:
− «Символьная логика»;
− «Алиса в стране чудес»;
− «Алиса в Зазеркалье».
Предмет исследования: использование системы естественно-математических знаний в произведениях Л.Кэррола.
Сформулированная цель, определила задачи нашего исследования:
изучение научной, математической, публицистической и художественной литературы по теме исследования;
− изучение, обобщение и систематизация основных логических понятий, связанных с темой исследования;
анализ, систематизация и обобщение материала, связанного с понятиями «логика», «логическое мышление», «парадокс»;
− выбор и анализ фрагментов произведений Л.Кэрролла, иллюстрирующих теоретические положения символьной логики, математические законы; физические явления.
Глава I. Логика Л.Кэрролла
Понятие логики
В соответствии с темой исследования возникла необходимость в выяснении содержания понятий логика, логическое мышление.
Логика − (λογική греч. logike от logos − слово, разум) − наука об общих законах развития объективного мира и познания (филос.). Формальная, логика идеалистической философии считает общие понятия и формы познания неизменными, раз навсегда данными. Логика диалектического материализма утверждает, что формы познания меняются вместе с изменением объективного мира, и потому является наукой об историческом развитии человеческого мышления, как отражения в сознании развития объективного мира;
− разумность, правильность умозаключений;
− внутренняя закономерность1.
Логика − «наука о правильном мышлении», «искусство рассуждения», о формах, методах и законах интеллектуальной познавательной деятельности, формализуемых с помощью логического языка. Поскольку это знание получено разумом, логика также определяется как наука о формах и законах правильного мышления. Поскольку мышление оформляется в языке в виде рассуждения, частными случаями которого являются доказательство и опровержение, логика иногда определяется как наука о способах рассуждения или наука о способах доказательств и опровержений. Логика как наука изучает способы достижения истины в процессе познания опосредованным путём, не из чувственного опыта, а из знаний, полученных ранее, поэтому её также можно определить как науку о способах получения выводного знания.
Одна из главных задач логики − определить, как прийти к выводу из предпосылок (правильное рассуждение) и получить истинное знание о предмете размышления, чтобы глубже разобраться в нюансах изучаемого предмета мысли и его соотношениях с другими аспектами рассматриваемого явления.
В словаре психологических понятий К.К. Платонова логическое мышление определяется как вид мышления, сущность которого заключается в ориентировании понятиями, суждениями и умозаключениями с использованием законов логики2. [с.62].
Д. Дьюи, исследуя понятие «логическое мышление», отмечает, что в широком смысле всякое мышление, приводящее к заключению, логическое, то есть термин логический покрывает как логически правильное, так и логически неверное. В более узком смысле термин логически относится только к тому, что доказано. Строгость доказательства является здесь синонимом логического. Но термин «логический» употребляется еще и в третьем смысле: как обозначение систематической работы. В этом смысле слово «логический» является синонимом осторожного, основательного, не поддающегося обману мышления3[с.59-60].
В психологии принято выделять две основные формы мышления: образное и вербально-логическое. Вербально-логическое. относится к высшему уровню отражения, связанному с абстракциями, обобщениями и оперированием знаковыми системами. Основными операциями, характерными для данного уровня, являются обобщение и абстрагирование, анализ и синтез (в вербально-логическом мышлении эти операции осуществляются с идеальными объектами, отражающими реальность в абстрактной и обобщенной форме), в том числе и такая его форма, как анализ через синтез4. К этим операциям относятся все виды умозаключений и аналогии.
Познание действительности осуществляется в двух основных формах − в форме чувственного познания и в форме абстрактного мышления. Абстрактное мышление позволяет из одних знаний получать другие, не обращаясь непосредственно к опыту, позволяет познавать мир в обобщенных формах (понятиях, суждениях, умозаключениях): обобщая полученные знания, люди посредством абстрактного мышления открывают законы природы, общества и познания, проникают в сущность явлений, закономерную связь между ними5 [с. 7].
Мышление в форме понятий называют понятийным. Высшей формой понятийного мышления является категориальное или структурное мышление. Категориями называются мыслительные структуры, в которых закрепляются существующие отношения вещей и явлений.
Обобщая определения, логическим мышлением будем называть мышление в форме понятий, суждений и умозаключений по правилам и законам логики, осуществляемое осознанно и развернуто в речи и с ее помощью.
В.Ф. Асмус указывает три теоретических положения относительно логического мышления: определенность, последовательность, доказательность. По его мнению, эти требования получают значение законов мышления только потому, что независимо от этих требований и до того, как они были впервые сформулированы логикой, имеют место в самом мышлении6[с. 6].
Способность делать из правильных посылок (суждений, утверждений) правильные выводы, находить правильные следствия из имеющихся фактов Л.М. Фридман называет логичностью как важным качеством мышления. Показателем развитого логического мышления человека является основательность мысли, дисциплинированность рассуждений, отсутствие ошибок в выводах и практической деятельности7[с. 14].
История развития логики
Л огика
появилась приблизительно в IV в. до н.э. в Древней Греции. Ее
создателем считается знаменитый древнегреческий философ и ученый
Аристотель (384-322 гг. до н. э.). Хотя, первое довольно
развернутое и систематическое изложение логических проблем
фактически дал более ранний древнегреческий философ и
естествоиспытатель Демокрит (460 − примерно 370 г. до н. э.). Среди
его многочисленных трудов был и обширный трактат в трех книгах «О
логическом, или О канонах» (от греч. kanon − предписание,
правило)8. Здесь не только были раскрыты
сущность познания, его основные формы и критерии истины, но и
показана огромная роль логических рассуждений в познании, дана
классификация суждений, подвергнуты решительной критике некоторые
виды выводного знания и предпринята попытка разработать
индуктивную логику − логику опытного знания.
огика
появилась приблизительно в IV в. до н.э. в Древней Греции. Ее
создателем считается знаменитый древнегреческий философ и ученый
Аристотель (384-322 гг. до н. э.). Хотя, первое довольно
развернутое и систематическое изложение логических проблем
фактически дал более ранний древнегреческий философ и
естествоиспытатель Демокрит (460 − примерно 370 г. до н. э.). Среди
его многочисленных трудов был и обширный трактат в трех книгах «О
логическом, или О канонах» (от греч. kanon − предписание,
правило)8. Здесь не только были раскрыты
сущность познания, его основные формы и критерии истины, но и
показана огромная роль логических рассуждений в познании, дана
классификация суждений, подвергнуты решительной критике некоторые
виды выводного знания и предпринята попытка разработать
индуктивную логику − логику опытного знания.
В средние века большой общественный резонанс получила проблема общих понятий − «универсалий». Спор о них растянулся на столетия.
В эпоху Возрождения логика переживала настоящий кризис. Она расценивалась в качестве логики «искусственного мышления», основанного на вере, которому противопоставлялось естественное мышление, базирующееся на интуиции и воображении.
Новый, более высокий этап в развитии логики начинается с XVII в. Этот этап органически связан с созданием в ее рамках наряду с дедуктивной логикой логики индуктивной. В ней нашли отражение многообразные процессы получения общих знаний на основе все более накапливавшегося эмпирического материала. Потребность в получении таких знаний наиболее полно осознал и выразил в своих трудах выдающийся английский философ и естествоиспытатель Ф. Бэкон (1561-1626). Он и стал родоначальником индуктивной логики. «... Логика, которая теперь имеется, бесполезна для открытия знаний», − вынес он свой приговор. В противовес старому «Органону» Аристотеля Бэкон написал «Новый Органон...», где и изложил индуктивную логику. Главное внимание в ней он обратил на разработку индуктивных методов определения причинной зависимости явлений. В этом огромная заслуга Бэкона. Однако созданное им учение об индукции по иронии судьбы оказалось не отрицанием предшествующей логики, а ее дальнейшим обогащением и развитием. Оно способствовало созданию обобщенной теории умозаключений. И это естественно, ибо, как будет показано ниже, индукция и дедукция не исключают, а предполагают друг друга и находятся в органическом единстве.
Индуктивная логика была позднее систематизирована и развита английским философом и ученым Дж. Ст. Миллем (1806-1873) в его двухтомном труде «Система логики силлогистической и индуктивной»9. Она существенно повлияла на дальнейшее развитие научного познания, способствовала достижению им новых высот.
П отребности
научного познания не только в индуктивном, но и в дедуктивном
методе в XVII в. наиболее полно воплотил французский философ и
ученый Рене Декарт (1596-1650). В своем главном труде «Рассуждение
о методе...», основываясь на данных, прежде всего математики, он
подчеркивал значение рациональной дедукции как основного метода
научного познания.
отребности
научного познания не только в индуктивном, но и в дедуктивном
методе в XVII в. наиболее полно воплотил французский философ и
ученый Рене Декарт (1596-1650). В своем главном труде «Рассуждение
о методе...», основываясь на данных, прежде всего математики, он
подчеркивал значение рациональной дедукции как основного метода
научного познания.
Последователи Декарта из монастыря в Пор-Рояле А. Арно и П. Николь создали труд «Логика, или Искусство мыслить». Он получил известность как «Логика Пор-Рояля» и долгое время использовался в качестве учебника по этой науке. В нем авторы вышли далеко за пределы традиционной логики и уделили главное внимание методологии научного познания, логике открытий10. Логика рассматривалась ими как познавательное орудие всех наук. Создание подобных «расширенных логик» стало характерным в XIX-XX вв.
В XIX в. появилась и стала быстро развиваться символическая или математическая, или современная логика, в основе которой лежат идеи, выдвинутые задолго до ХIХ в. немецким математиком и философом Готфридом Лейбницем (1646-1716 гг.), об осуществлении полного перехода к идеальной (т.е. совершенно освобожденной от содержания) логической форме при помощи универсального символического языка, аналогичного языку алгебры. Лейбниц говорил о возможности представить доказательство как математическое вычисление11.
Ирландский логик и математик Джордж Буль (1815-1864 гг.) истолковал умозаключение как результат решения логических равенств, в результате чего теория умозаключений приняла вид своеобразной алгебры, отличающейся от обычной алгебры лишь отсутствием численных коэффициентов и степеней. Таким образом, одно из основных отличий символической логики от традиционной заключается в том, что в последней при описании правильного мышления используется обычный, или естественный язык; а символическая логика исследует тот же предмет (правильное мышление) с помощью построения искусственных, специальных, формализованных языков, или, как их еще называют, исчислений.
Т радиционная
и символическая логика не являются, как может показаться,
различными науками, а представляют собой два последовательных
периода в развитии одной и той же науки: основное содержание
традиционной логики вошло в символическую, было в ней уточнено и
расширено, хотя многое при этом оказалось переосмысленным.
радиционная
и символическая логика не являются, как может показаться,
различными науками, а представляют собой два последовательных
периода в развитии одной и той же науки: основное содержание
традиционной логики вошло в символическую, было в ней уточнено и
расширено, хотя многое при этом оказалось переосмысленным.
Известный вклад в развитие традиционной формальной логики внесли русские ученые. Так, уже в первых трактатах по логике начиная приблизительно с X в. предпринимались попытки самостоятельного комментирования трудов Аристотеля и других ученых. Оригинальные логические концепции в России разрабатывались в XVIII в. и были связаны прежде всего с именами М. Ломоносова (1711-1765) и А. Радищева (1749-1802). Расцвет логических исследований в нашей стране относится к концу XIX в. Так, М. Каринский (1840-1917) создал оригинальную общую теорию выводов − как дедуктивных, так и индуктивных. Труды его ученика Л. Рутковского (1859-1920) были посвящены основным типам умозаключений, их дальнейшей разработке. С. Поварнин (1870-1952) стремился разработать общую теорию отношений в логике. Дальнейшее развитие традиционная логика получила в годы Советской власти. Она успешно разрабатывается и в наши дни.
Символическая логика
Символи́ческая ло́гика − направление в математической логике, изучающее формальные системы: «логика по предмету, математика по методу» (П. С. Порецкий), или «логика, изучаемая посредством построения формализованных языков» (А. Чёрч). Термин «символическая логика» акцентирует внимание на том обстоятельстве, что основными элементами формализованных языков, служащих «математическим методом» изучения предмета логики, являются в данном случае не слова обычных разговорных языков, а некоторые символы, выбираемые и интерпретируемые определённым образом, специфическим именно для данной логической ситуации и, вообще говоря, не связанным ни с каким «традиционным» употреблением, пониманием и функциями таких же символов в других контекстах.
Подлинную революцию в логических исследованиях вызвало создание во второй половине XIX в. математической логики, которая получила еще название символической и обозначила новый, современный этап в развитии логики
Зачатки этой логики прослеживаются уже у Аристотеля, а также у его последователей, стоиков в виде элементов логики предикатов и теории модальных выводов, а также логики высказываний. Однако систематическая разработка ее проблем относится к гораздо более позднему времени.12
Растущие успехи в развитии математики и проникновение математических методов в другие науки уже во второй половине XVII в. настоятельно выдвигали две фундаментальные проблемы. С одной стороны, это применение логики для разработки теоретических оснований математики, а с другой − математизация самой логики как науки. Наиболее глубокую и плодотворную попытку решить вставшие проблемы предпринял крупнейший немецкий философ и математик Г. Лейбниц (1646-1416) Тем самым он стал, по существу, зачинателем математической (символической) логики. Лейбниц мечтал о том времени, когда ученые будут заниматься не эмпирическими исследованиями, а исчислением с карандашом в руках. Он стремился изобрести для этого универсальный символический язык, посредством которого можно было бы рационализировать любую эмпирическую науку. Новое знание, по его мнению, будет результатом логической калькуляции − исчисления.
Идеи Лейбница получили некоторую разработку в XVIII в. и первой половине XIX в. Однако наиболее благоприятные условия для мощного развития символической логики сложились лишь со второй половины XIX в. К этому времени математизация наук достигла особенно значительного прогресса, а в самой математике возникли новые фундаментальные проблемы ее обоснования. Английский ученый, математик и логик Дж. Буль (1815-1864) в своих работах, прежде всего, применял математику к логике. Он дал математический анализ теории умозаключений, выработал логическое исчисление («Булева алгебра»). Немецкий логик и математик Г. Фреге (1848-1925) применил логику для исследования математики. Посредством расширенного исчисления предикатов он построил формализованную систему арифметики. Английский философ, логик и математик Б. Рассел (1872-1970) совместно с А. Уайтхедом (1881-1947) в трехтомном фундаментальном труде «Принципы математики» в целях ее логического обоснования попытался осуществить в систематической форме дедуктивно-аксиоматическое построение логики.
Так открылся новый, современный этап в развитии логических исследований. Пожалуй, наиболее важная отличительная особенность этого этапа состоит в разработке и использовании новых методов решения традиционных логических проблем. Это разработка и применение искусственного, так называемого формализованного языка − языка символов, т.е. буквенных и других знаков (отсюда и наиболее общее наименование современной логики − «символическая»).
Различают два вида логических исчислений: исчисление высказываний и исчисление предикатов. При первом допускается отвлечение от внутренней, понятийной структуры суждений, а при втором эта структура учитывается и соответственно символический язык обогащается, дополняется новыми знаками.
Значение символических языков в логике трудно переоценить. Г. Фреге сравнивал его со значением телескопа и микроскопа. А немецкий философ Г. Клаус (1912-1974) считал, что создание формализованного языка имело для техники логического вывода такое же значение, какое в сфере производства имел переход от ручного труда к машинному. Возникая на основе традиционной формальной логики, символическая логика, с одной стороны, уточняет, углубляет и обобщает прежние представления о логических законах и формах, особенно в теории выводов, а с другой − все более значительно расширяет и обогащает логическую проблематику. Современная логика − сложнейшая и высокоразвитая система знаний13. Она включает в себя множество отдельных, относительно самостоятельных «логик», все более полно выражающих запросы практики и в конечном счете отражающих многообразие и сложность окружающего мира, единство и многообразие самого мышления об этом мире.
Символическая логика находит все более широкое применение в других науках − не только в математике, но и в физике, биологии, кибернетике, экономике, лингвистике. Она приводит к возникновению новых отраслей знаний (метаматематика). Особенно впечатляюща и наглядна роль современной логики в сфере производства. Открывая возможность как бы автоматизировать процесс рассуждений, она позволяет передать некоторые функции мышления техническим устройствам. Ее результаты находят все более широкое применение в технике: при создании релейно-контактных схем, вычислительных машин, информационно-логических систем и т. д. По образному выражению одного из ученых, современная логика − это не только «инструмент» точной мысли, но и «мысль» точного инструмента, электронного автомата. Специально отметим, что достижения современной логики используются и в правовой сфере. Так, в криминалистике на разных этапах исследования производится логико-математическая обработка собранной информации.
Растущие потребности научно-технического прогресса обусловливают дальнейшее интенсивное развитие современной логики.
В разработку систем символической логики внесли важный вклад русские ученые. Среди них особенно выделяется П. Порецкий (1846-1907). Так, он первым в России начал чтение лекций по математической логике. Его собственные труды в этой области не только были на уровне трудов современных ему западноевропейских ученых, но и в ряде случаев превосходили их.
Символическая логика Льюиса Л.Кэрролла
Первое знакомство с первой частью «Символической логики» Л.Кэрролла14 поражает оригинальностью и глубиной мысли автора, тщательностью и продуманностью не только отдельных положений, но и широкого плана построения целостной логической теории. Л.Кэрролл опубликовал только первую часть своего фундаментального труда и ее популярную версию «Логическая игра». Им была подготовлена вторая часть, корректура которой была найдена в архиве профессора Кука Вилсона.
Характерной чертой логической системы Л.Кэрролла является то, что она не является плодом чисто умозрительных построений автора. Наоборот, логика Л.Кэрролла носит сугубо практический характер. Она предназначена для непосредственного решения сложнейших логических и математических задач. Автор сознательно проверяет ее в «экстремальных» случаях, его привлекает прежде всего логический анализ суждений, по меньшей мере странных с точки зрения здравого смысла. Его основная цель - сформулировать предельно общие формулы и правила получения нового знания, которые, подобно улыбке Чеширского кота, остаются после того, как здравый смысл из посылок исчезает.
Глубина поднимаемых Л.Кэрроллом логико-философских вопросов, оригинальность их решения отмечались в свое время Б.Расселом. Речь идет об анализе Л.Кэрроллом понятия существования в логике, о возможности получения в его логике заключения из отрицательных посылок, о необычном методе диаграмм, превосходящем эвристическими возможностями хорошо известные диаграммы Л.Эйлера и Д.Венна, об обосновании форм правильного вывода, которые позволяют получать множество новых видов умозаключений, не известных в аристотелевской логике и многом, многом другом.
Несмотря на столь явные достоинства, новаторские идеи и методы Л.Кэрролла не были своевременно оценены по достоинству, а имя его незаслуженно обойдено в учебниках по истории логики. Правда, отмечая этот прискорбный факт исторической несправедливости, следует учитывать, что одновременно с автором «Символической логик» (годы жизни Л.Кэрролла − 1832-1898) жили и творили такие авторитеты в логике как У.Гамильтон (1788-1856), Д.С.Милль (1806-1873), Г.Лотце (1806-1881), У.Джевонс (1835-1882), А. де Морган (1806-1878), Д.Венн (1834-1923), Г.Фреге и, наконец, основатель современных математических методов в логике − Д.Буль (1815-1864). Творчество Л.Кэрролла выпадает как раз на тот период, когда велись активные поиски развития методов формальной логики, по внедрению в логику математических методов, приведших впоследствии к развитию мощного аппарата математической логики. Немудрено поэтому, что логические труды признанного литератора, но мало кому известного преподавателя элементарной геометрии в Оксфорде, остались незамеченными в логической литературе15.
О днако
вряд ли прав переводчик «Символической логики» на русский язык
Ю.Данилов, когда представляет Л.Кэрролла самоучкой, не имевшим
достаточного логического образования. Л.Кэрролл состоял в активной
творческой переписке с Д.Венном, им тщательнейшим образом изучена
силлогистика Аристотеля. Да и вообще, вряд ли, работая в Оксфорде,
он оставался в стороне от современных ему идей математики и логики.
О широкой логической эрудиции Л.Кэрролла свидетельствует не только
глубина его логико-семантических разработок, но и рассыпанные по
многим страницам «Символической логик» критические замечания и
ответы на возражения возможным, хотя и безымянным критикам.
Показательно и само название этой работы. До сих пор считается, что
термин «символическая логика» впервые введен в обиход Д.Венном,
работа которого, под таким названием вышла впервые в 1881 года, а
вторым изданием − в 1894.
днако
вряд ли прав переводчик «Символической логики» на русский язык
Ю.Данилов, когда представляет Л.Кэрролла самоучкой, не имевшим
достаточного логического образования. Л.Кэрролл состоял в активной
творческой переписке с Д.Венном, им тщательнейшим образом изучена
силлогистика Аристотеля. Да и вообще, вряд ли, работая в Оксфорде,
он оставался в стороне от современных ему идей математики и логики.
О широкой логической эрудиции Л.Кэрролла свидетельствует не только
глубина его логико-семантических разработок, но и рассыпанные по
многим страницам «Символической логик» критические замечания и
ответы на возражения возможным, хотя и безымянным критикам.
Показательно и само название этой работы. До сих пор считается, что
термин «символическая логика» впервые введен в обиход Д.Венном,
работа которого, под таким названием вышла впервые в 1881 года, а
вторым изданием − в 1894.
Тем не менее, можно сказать, что близкое знакомство с идеями одного из самых оригинальных и интересных британских мыслителей XIX века − дело еще далеко не завершенное, в том числе − в России. Прошла уже почти четверть века с появления первой отечественной работы, посвященной систематическому анализу логики Льюиса Л.Кэрролла16. За это время найдены и опубликованы материалы III-й и IV-й частей его «Символической логики», вышла на русском языке «Логическая игра»17, опубликована серия статей и защищена диссертация Н.Г.Колесникова18, эвристический потенциал Л.Кэрролловских диаграмм признан не только специалистами по искусственному интеллекту, но и отмечен в энциклопедических изданиях.
Однако логика Л.Кэрролла до сих пор остается маргинальной темой в логической литературе. Время показывает, что обращение к Кэрролловскому наследию важно не столько в целях знакомства с его системой, сколько в целях применения некоторых перспектив и возможностей, которые она открывает.
Кэрролловский метод диаграмм
Л.Кэрроллом были предложены два метода логического анализа − диаграммы и индексная запись. Причем ведущую эвристическую роль играют диаграммы. Этот метод основан на классификации универсума рассмотрения с помощью конкретных свойств (признаков).
Пусть диаграмма

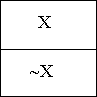
представляет конкретный универсум. Если воспользоваться неким признаком, например, Х, то универсум может быть поделен на две ячейки: X и ~X (не-Х):
Далее можно, взяв другой признак, например, Y разделить универсум на еще две части. Таким образом, мы получим «двухбуквенную» диаграмму Л.Кэрролла:
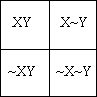
Условимся далее, что знак 1 означает, что данная клетка универсума занята (в ней имеется хотя бы один предмет, наделенный такой комбинацией свойств). Л.Кэрролл для этой цели чаще использует красную фишку (кружок). Знак 0, стоящий в клетке означает, что эта клетка пуста − таких предметов не существует.
На таких диаграммах можно легко представить простые суждения. Л.Кэрролл называет их «суждениями существования» или «нормальными формами». Представим диаграммы для традиционных четырех видов простых суждений: (A) − общеутвердительных (все X есть Y); (E) − общеотрицательных (все X не естьY); (I) − частноутвердительных (некоторые X есть Y) и (O) − частноотрицательных (некоторые X не есть Y):(I)
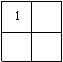
Некоторые X суть Y=Некоторые Y суть Х=XY существуют=Существуют XY
(O)

Некоторые Х суть ~Y=Некоторые ~Y суть Х=X~Y существуют= =Существуют X~Y
Таким образом, согласно Л.Кэрроллу, частноотрицательное суждение является разновидностью частноутвердительного.(E)

Ни один X не сутьY=Ни один Y не суть Х=Ни один XY не существует=Не существует XY
(A)
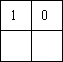
Все Х суть Y=(Ни один Х не суть ~Y)+(Некоторые Х суть Y)=(Не существуют X~Y)+
+(Существуют XY) = …
Таким образом, в логике Л.Кэрролла существует только два типа простых суждений: I и E. Он называет их «реальностями» и «химерами» соответственно. О-суждения − разновидность I-суждений, а общеутвердительные суждения состоят из одной химеры и одной реальности. В этом он радикально расходится с традиционной трактовкой, согласно которой А-суждения чисто обратимы в общеотрицательные. В трактовке же Л.Кэрролла такой общеотрицательный эквивалент дополняется «реальностью», в которой подчеркивается непустота субъекта исходного суждения.
Если учесть возможность перемены мест субъекта и предиката, а также допущение отрицательных терминов-субъектов и терминов-предикатов, то очевидно, что такая трактовка, с одной стороны, упрощает силлогистику, с другой − резко увеличивает число возможных корректных модусов умозаключений.
Силлогистическое рассуждение − вид рассуждения, где требуется определить, следует ли из двух или нескольких утверждений данное заключение. Одним из видов силлогизмов является категорический силлогизм. Категорический силлогизм включает в себя кванторные слова, или термины, указывающие на количество. Кванторными словами являются такие термины, как «все», «некоторые» и «ни один». Они показывают, сколько элементов принадлежит к определенной категории.
Обычно силлогизм состоит из двух утверждений, которые называются посылками, и третьего утверждения, которое называется заключением. В категорических силлогизмах в посылках и заключении присутствуют кванторные слова. Задача заключается в том, чтобы определить, является ли заключение логическим следствием посылок.
Посылки и заключение силлогизма классифицируются по наклонениям (moods). Существует четыре вида наклонений, или сочетаний положительных и отрицательных утверждений с терминами «все» и «некоторые». Эти четыре вида наклонений приводятся ниже.
Суждение является общим, если оно содержит термины «все» или «ни один», частным − если содержит термин «некоторые», отрицательным − если содержит «не», и утвердительным, если оно не является отрицательным. Таким образом, вид суждения определить довольно легко, если найти в нем ключевые термины.
Умозаключения − собственно силлогизмы − предполагают построение трехбуквенных диаграмм, на которые наносятся суждения посылки:
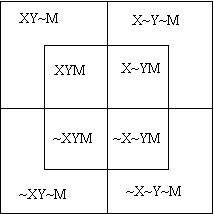
Например, возьмем посылки:
Все эгоистичные люди неприятны окружающим.
Все обязательные люди приятны окружающим.
В традиционной логике из них может быть получено общеотрицательное заключение: Все обязательные люди не эгоистичны.
Проверим его на диаграммах Л.Кэрролла. Универсум − люди. X − эгоистичные. Y − обязательные. M − приятные окружающим:
По Л.Кэрроллу традиционное заключение оказывается неполным. Полное заключение содержит еще одно суждение:
Все эгоистичные люди необязательны.
Метод Л.Кэрролла обладает несомненными эвристическими преимуществами перед другими методами диаграмм: Л.Эйлера и Д.Венна.
Метод Эйлера основан на сопоставлении понятию − круга, который изображает объем данного понятия (класс соответствующих предметов). Для изображения суждений как субъектно-предикатных структур используются простейшие комбинации двух кругов, соответствующих объемам субъекта и предиката:
Такая диаграмма используется для изображения суждений: «все Х суть Y», «ни один X не есть не-Y», «некоторые Y суть X», «некоторые Y суть не-X» и суждений, обратным четырем последним.
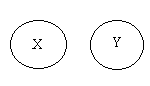
Эта диаграмма используется в представлении суждений: «все Х суть не-Y», «Все Y суть не-Х», «ни один Х не есть Y», «некоторые не-Х суть Y», «некоторые не-Y суть Х», «все не-Х суть не-Y»
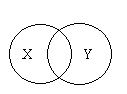
Эта диаграмма используется в представлении суждений: «некоторые Х суть Y», «некоторые Х суть не-Y», «некоторые не-Х суть Y», «некоторые не-Y суть Х» и обратные им.
Таким образом, метод Эйлера обладает интересной особенностью - все эйлеровы диаграммы содержат суждение «некоторые не-Х суть не-Y». Это позволяет Л.Кэрроллу саркастически заметить: «По-видимому, Эйлеру никогда не приходило в голову, что это утверждение иногда может оказаться ложным!»19 Кроме того, для изображения этого суждения потребуется весь набор диаграмм.
Что касается метода Д.Венна, то он пользуется двумя кругами, в которых заштрихованная часть означает пустой класс (по техническим причинам мы там ставим 0), а непустая, «занятая» часть отмечается крестиком:
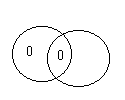
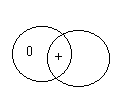
Некоторые Х суть Y
Ни один X не есть Y
Все X суть Y
Таким образом, для четырех возможных классов XY, X~Y, ~XY и ~X~Y лишь первым трем соответствуют клетки конечных размеров. Четвертому же классу отводится вся остальная часть бесконечной плоскости. Столкнувшись с необходимостью изобразить суждение «ни один не-Х не сть не-Y», Венн замечал, что «не следует стараться заштриховывать всю внешнюю часть диаграммы».
Д ля
изображения двух суждений с одним общим термином надо прибегать к
помощи трехкруговой диаграммы, на которой для размещения восьми
возможных классов имеется семь клеток конечных размеров:
ля
изображения двух суждений с одним общим термином надо прибегать к
помощи трехкруговой диаграммы, на которой для размещения восьми
возможных классов имеется семь клеток конечных размеров:
Для четырех терминов потребуется уже сложная фигура из пересеченных эллипсов, дающая 15 конечных клеток. Для пяти терминов - еще более сложное построение с 31 клеткой. Причем один из эллипсов надо будет считать лежащим в плоскости вне одного из остальных. Для шести терминов потребуются две пятибуквенные диаграммы. Дальше шести терминов Д.Венн не идет.
Л.Кэрролловские же диаграммы легко распространяются на 4 термина − в этом случае получаются 16 клеток. Для пяти терминов используются 32 клетки, для шести − 64, для семи − 128, для восьми − 256, для девяти − 512 (две соприкасающиеся восьмибуквенные диаграммы), для десяти − 1024 (квадрат из четырех восьмибуквенных диаграмм) и т.д.
Фактически, метод Л.Кэрролла является развитием и усовершенствованием метода Венна. Различия касаются только графики: у Венна − круги и ячейки ограничиваются кривыми линиями, а у Л.Кэрролла − прямыми. Кроме того, у Л.Кэрролла класс ~X~Y занимает такую же ограниченную часть плоскости, что и другие классы.
Интересно, что уже в ХХ столетии У.Маккаллок и его последователи, применившие диаграммы Венна (на которого Маккаллок и ссылается) для моделирования сетей формальных нейронов, пользовались, фактически, диаграммами Л.Кэрролла. Сначала Маккалок чертил круги в духе Эйлера-Венна, а затем стал пользоваться ихфрагментом, как общим случаем20:
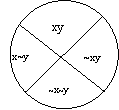
Диаграмма Венна (прямоугольником
выделена часть, аналогичная диаграмме
Л.Кэрролла - Маккаллока)
Диаграмма Маккаллока - прямой аналог диаграммы Л.Кэрролла
Представляя в таких диаграммах информацию, Маккалок первоначально ставил в точки в значимых ячейках, потом пользовался знаками 0 и 1, перейдя затем к теоретико-вероятностным (многозначным) моделям. Д.Коэн показал возможность применения маккалоковского подхода для выражения не только функций Буля-Шредера, но и более общих функций Льюиса, а также Поста-Лукасевича, т.е. к аппарату многозначных и модальных логик21.
Отечественный исследователь диаграмм Венна − А.Кузичев показал, что модернизированные Маккаллоком в 1943 году диаграммы Венна позволяют адекватно выражать содержание не только алгебры логики Д.Буля, но и логики высказываний и логики предикатов22. В 1972 году венгерскими логиками Д.Бизамом и Я.Герцогом был предложен табличный метод решения логических задач23. Д.Бизам и Я.Герцог строят таблицы (матрицы) всех возможных комбинаций терминов, фигурирующих в рассуждении, чтобы затем, на основе информации, содержащейся в условиях задачи, вычеркнуть невозможные комбинации. Остающиеся клетки − и есть итоговое заключение. Фактически, речь идет о диаграммах Л.Кэрролла с использованием исключительно общеотрицательных суждений.
Одно из излюбленных обвинений формальной логики - обвинение в банальности и тавтологичности - так как она не дает прироста информации. Знание, выраженное в заключении, уже якобы, содержится в посылках. Поэтому силлогизм не обладает доказательной силой, поскольку якобы содержит логическую ошибку «предвосхищения основания», когда утверждается нечто, что еще требуется доказать:
Столь грозное, на первый взгляд, обвинение просто и изящно отводится в Л.Кэрролловском методе диаграмм, которым наглядно демонстрируется: чтобы информацию, содержащуюся в двух посылках, трансформировать в новое суждение (считать информацию с трехбуквенной диаграммы и перенести ее в двухбуквенную), необходимо взаимодействие содержания информации, содержащейся в каждой из посылок. В этом плане, Л.Кэрролловская логика может рассматриваться как интенсиональная в своих основаниях, как логика содержательных, а не объемных логических отношений по преимуществу.
Как известно, у любого понятия есть две основные характеристики: объем и содержание. Первая связана с совокупностью предметов, знание которых фиксировано в понятии. Содержание − признаки предметов, знание о которых выражено в понятии. Вопрос о том, что определяет − объем содержание или содержание объем сродни знаменитому спору о курице и яйце. Если первичен объем, то познание начинается с предметов и лишь затем мы выделяем признаки, их характеризующие. Если первично содержание, то познание начинается с признаков, из которых потом «лепятся» предметы. Или иначе - то ли множество определяет свойства, объединяющее элементы множества, то ли само это свойство определяет принадлежность предметов этому множеству.
У Л.Кэрролла классы определяются интенсионально, т.е. наличием или отсутствием признаков предметов. Универсум рассуждения Л.Кэрролл трактует как пространство признаков, упорядочение которых и составляет предмет логики. Таким образом, уже с самого начала просматривается отличие подхода Л.Кэрролла от привычного сейчас экстенсионального подхода к семантике. Современные логика и логическая семантика строятся преимущественно как системы анализа отношений объемов понятий.
Элементы логики содержания можно найти еще в силлогистике Аристотеля. Как отмечает Маковельский, «теория категорического силлогизма возникла из критики платоновского учения об определении понятия путем логического деления». Однако непосредственно саму силлогистику Аристотель строит смешанным путем. Так, интерпретируя термины как роды и виды (т.е. экстенсионально), он, в то же время, раскрывает отношения между ними как отношения присущности признаков (т.е. интенсионально). Например, первая фигура в «Аналитике» выглядит следующим образом:
В присуще С
А присуще В
Следовательно, А присуще С
Обусловлена такая нечеткость, очевидно, тем, что во времена Аристотеля еще не была выработана ясная дистинкция между объемом и содержанием понятия. Со времен схоластов в традиционной «школьной» логике первая фигура понимается несколько иначе:
В есть С
А есть В
Следовательно, А есть С
В этом случае связка «есть» трактуется как «объем понятия X входит в объем понятия Y.» Наглядное представление об объемной интерпретации логических отношений дают диаграммы Эйлера и, правда, в меньшей степени, диаграммы Венна.
Именно с экстенсиональным подходом связаны магистральные пути развития современной логической науки: булева алгебра, математическая логика Г.Фреге, Б.Рассела, Д.Гильберта. Связано это, очевидно, с большей разработанностью анализа объемных отношений в силу их большей простоты и использования математических методов: алгебры (Д.Буль, Г.Шредер, С.Порецкий и др.), функциональной трактовки понятий (Г.Фреге), теоретико-множественных и теоретико-вероятностных подходов в новейшее время. Математика же строится преимущественно на основе теории множеств, т.е. экстенсионально.
Развитие логики содержания после Аристотеля можно найти в логике стоиков, в основе которой лежит не общепринятая в Средние века аксиома силлогизма dictum de omni et nullo и не объемное отношение терминов в силлогизме, а трактовка вещи как совокупности качеств. Поэтому логика стоиков строится на интенсиональном принципе «признак признака вещи есть признак вещи».
В принципе, традиция логики содержания прослеживается на протяжении всей истории логики, ее элементы можно найти в учениях Р.Декарта, логиков Пор-Рояля, Лейбница. К этой традиции, в известной степени, примыкает и Л.Кэрролл. Его не интересует, отражено в посылках реальное положение дел или нет. Важно, что если бы посылки были бы истинными, то и заключение с необходимостью было бы истинным суждением. В его логике рассматриваются изначально все возможные мыслимые ситуации. Решение же вопроса о реальности существования элементов универсума (характеризуемых некими комплексами свойств) дело не логики, а теории познания и конкретной методологии, в конце концов - каждой конкретной науки и сферы деятельности. Логика же интересуют всеобщие закономерности, необходимые связи между признаками.
В этом случае преодолеваются трудности с поиском адекватного выражения логического (необходимого) следования, решения парадоксов материальной, сильной, строгой и релевантной импликаций, поскольку логические отношения − суть необходимые отношения, а отношение следования есть фиксация факта необходимости сосуществования данных признаков. Поэтому само понятие следования Л.Кэрроллом трактуется не как некий функтор, а, как и у Г.Лотце, с помощью бинарного метапредиката.
Аристотелем в «Топике» была предложена концепция предикации, согласно которой в качестве предиката суждении могут выступать:
(1) Родовое понятие − например, «человек − животное»;
(2) Случайный признак − например, «человек − сидит»;
(3) Определяющее в определении − например, «человек − животное, обладающее разумом»;
(4) Собственный признак, т.е. часть сущности вида − например, − «человек обладает способностью к речи»24.
Л.Кэрролл все это разнообразие предикации сводит, фактически, ко второму случаю. Он допускает все возможные комбинации признаков и рассматривает, каковы логически необходимые следствия допущения конкретных комбинаций.
В логике его интересуют только признаки: x, y, z, m и т.д. Он оперирует с полем признаков. Индивиды же интересуют его лишь постольку, поскольку они являются носителями признаков, распределенных в универсуме. Эта глубокая идея перекликается с идеей Г.Лотце, непонятой историком логики П.С.Поповым, который критиковал Лотце за ненужное якобы повторение понятия «люди» в суждении «Некоторые люди суть черные люди»25. П.С.Попов полагает, что Г.Лотце здесь отходит от своей же концепции логики содержания, поскольку подводит понятие «черные люди» под более общее понятие «люди». Однако в логике содержания, тем более в концепции Л.Кэрролловских нормальных форм суждения, эти аргументы снимаются.
В логике содержания нас интересуют отношения не классов, а признаков в поле конкретного универсума. В данном случае универсумом рассуждения являются люди. Не случайно Л.Кэрролл постоянно подчеркивает в «Символической логике», что всякая классификация − мысленный процесс группировки индивидов по определенным свойствам. Сам же индивид всегда более общ, чем предикаты, фигурирующие в любом рассуждении − по одной простой причине, что количество возможных наборов таких предикатов бесконечно.
Именно с этой методологической позиции Л.Кэрролл и предпринял свою основательную критику традиционной силлогистики, согласно которой из двух отрицательных посылок невозможен правильный вывод. Л.Кэрролл считал эту концепцию «еще одним пунктом помешательства логиков, столь же патологическим, как и их паническая боязнь отрицательных признаков»26. Он предлагает рассмотреть следующие пары суждений:
Ни один из моих мальчиков не жаден
Ни одна из моих девочек не жадна
Ни один из моих мальчиков не умен
Только умный мальчик мог бы решить эту задачу
Ни один из моих мальчиков не окончил школу
Некоторые из моих мальчиков не поют в хоре
Из каждой пары можно сделать заключение (соответственно):
Никто из моих мальчиков и девочек не жаден
Никто из моих мальчиков не мог бы решить эту задачу
Некоторые мальчики, не окончившие школу, не поют в хоре
Причем, последние суждения в логике Л.Кэрролла надлежит рассматривать как утвердительные, в то время как в традиционной логике их сочтут отрицательными. Л.Кэрролл иронически замечает: «Если вы, дорогой читатель, подробно рассмотрев все три пары посылок, обнаружите, что не можете вывести заключение ни из одной из них, мне не останется ничего другого, как повторить слова, сказанные персонажем в одной пьесе: «Вам придется поверить в то, в чем мы искренне уверены»».27
И здесь, в критике ограниченности традиционного объемного понимания логических отношений, Л.Кэрролл − единомышленник Г.Лотце. Но если немецкий логик наметил только общие черты логики содержания, то его британский современник дал первый конструктивный образец ее.
Диаграммы Л.Кэрролла − это графическое изображение всех возможных описаний состояния универсума, полученных с применением конкретных средств описания (терминов). Можно сказать, что это графический аналог описаний состояния (возможных миров) в духе Р.Карнапа.
Логика Л.Кэрролла − естественным образом логика необходимых связей. Л.Кэрролловские правила вывода (например, считывания информации с 3-х и более буквенной диаграммы) есть правила получения необходимого знания на основании знания о существовании предметов определенного вида. Причем, мы только предполагаем их существование, т.е. если мир устроен так, что наши посылки истинны (например, коты-гувернеры существуют), то мы с необходимостью получаем заключение. Подтверждение же таких экзистенциальных (онтологических, как сказал бы У.Куайн) допущений производится внелогическим путем. Логика Л.Кэрролла не нуждается в экзистенциальных (онтологических) допущениях о предметной области, поскольку сама является «теорией виртуального существования»28.
Рассмотрим некоторые задания из «Символической логики» Л. Кэрролла.
Задание.
Ваш курс всегда честен.
Ваш курс - лучшая политика.
Решение. Введём следующие обозначения:
Универсум u − курсы, m − ваши, x − честные, y − курсы, являющиеся лучшей политикой.
M = AmxAmy = (m'+x)(m'+y) = m'+xy.
F(x,y)
00
i
01
i
10
i
11
1
F(x,y) = xy+i = Ixy(3), т.е. «Честный курс - иногда лучшая политика».
Задание.
Ни одно жирное животное не может бегать быстро.
Некоторые гончие бегают быстро.
Решение. Введём следующие обозначения:
Универсум u − животные, m - быстрые, x − жирные, y - гончие.
M = ExmIym(8) = (m'+x') & 1 = m'+x'.
F(x,y) = x'+i = Ix'y(5).
F(x,y)
00
1
01
1
10
i
11
i
F(x,y) = x'+i = Ix'y(5), т.е. «Некоторые гончие не жирные».
-
Свиньи не летают.
Свиньи прожорливы.
-
Джон трудолюбив.
Ни один трудолюбивый человек не несчастен.
-
Некоторые законы о налогах несправедливы.
Все законы, принятые на прошлой неделе, относятся к налогообложению.
-
Ни один военный не пишет стихов.
Ни один из моих жильцов не штатских.
-
Ни одно лекарство не приятно на вкус.
Александровский лист - лекарство.
-
Некоторые циркуляры не доставляют удовольствия.
Ни одно письмо, в котором содержится какая-нибудь просьба, не доставляет удовольствия.
-
Все осы злые.
Всех злых существ необходимо остерегаться.
Кэрролловская логика в сказках об Алисе
 Закон
исключенного третьего
Закон
исключенного третьего
Закон исключительного третьего, как и закон противоречия, устанавливает связь между противоречащими друг другу высказываниями: из двух противоречащих высказываний одно является истинным.
«Аристотель умер в 322 г. до н.э. или он не умер в этом году»,
«Личинки мух имеют голову или не имеют ее».
Истинность отрицания равнозначна ложности утверждения. В силу этого закон исключенного третьего можно передать и так: каждое высказывание является истинным или ложным.
Этот закон с иронией обыгрывается в художественной литературе. Причина иронии понятна: сказать «Нечто или есть, или его нет», значит, ровным счетом ничего не сказать. И смешно, если кто-то этого не знает.
В известной сказке Л.Кэрролла «Алиса в Зазеркалье» Белый Рыцарь намерен спеть Алисе «очень, очень красивую песню».
- Когда я ее пою, все рыдают... или...
- Или что? - спросила Алиса, не понимая, почему Рыцарь вдруг остановился.
- Или... не рыдают...
Аналогия
Существует интересный способ рассуждения, требующий не только ума, но и богатого воображения, исполненный поэтического полета, но не дающий твердого знания, а нередко и просто вводящий в заблуждение. Этот очень популярный способ - умозаключение по аналогии.
Рассуждение идет по схеме: сопоставляются два объекта и оказывается, что они сходны в каких-то своих признаках. Из этого делается вывод, что их сходство распространяется и на другие, еще не рассматривавшиеся признаки. При таком рассуждении знание, полученное из рассмотрения одного предмета, переносится на другой менее изученный предмет. Это и есть умозаключение по аналогии.
Нередко аналогией называют рассуждения, заведомо не являющиеся умозаключениями по аналогии.
В сказке Л.Кэрролла «Алиса в Стране чудес» есть такой диалог.
Алиса спрашивает Чеширского кота:
− А откуда вы знаете, что вы не в своем уме?
− Начнем с того, что пес в своем уме. Согласна?
− Допустим, − согласилась Алиса.
− Дальше, − сказал кот. − Пес ворчит, когда сердится, а когда доволен, виляет хвостом. Ну а я ворчу, когда я доволен, и виляю хвостом, когда сержусь. Следовательно, я не в своем уме.
Кот сравнивает здесь свое поведение с поведением пса в тех же обстоятельствах, или, как обычно говорят, проводит аналогию. Однако рассуждение кота − это не умозаключение по аналогии. Последнее требует, чтобы на основе сходства известных черт делался вывод о совпадении и других черт. Этого в данном случае нет. Пес в своем уме, из чего кот заключает, что сам он, в противоположность псу, явно не в своем уме.
А налогия
обладает слабой доказательной силой. Продолжение сходства может
оказаться поверхностным или даже ошибочным. Однако доказательность
и убедительность далеко не всегда совпадают. Нередко строгое,
проводимое шаг за шагом доказательство оказывается неуместным и
убеждает меньше, чем мимолетная, но образная и яркая аналогия.
Доказательство − сильнодействующее средство исправления и
углубления убеждений, в то время как аналогия подобна
гомеопатическому лекарству, принимаемому ничтожными дозами, но
оказывающему тем не менее заметный лечебный эффект.
налогия
обладает слабой доказательной силой. Продолжение сходства может
оказаться поверхностным или даже ошибочным. Однако доказательность
и убедительность далеко не всегда совпадают. Нередко строгое,
проводимое шаг за шагом доказательство оказывается неуместным и
убеждает меньше, чем мимолетная, но образная и яркая аналогия.
Доказательство − сильнодействующее средство исправления и
углубления убеждений, в то время как аналогия подобна
гомеопатическому лекарству, принимаемому ничтожными дозами, но
оказывающему тем не менее заметный лечебный эффект.
В абсурде Кэрролла строгая, почти математическая система.
«Едят ли кошки мошек?… Едят ли мошки кошек?» − твердит сонная Алиса, меняя действующих лиц местами.
«Вот судья», − размышляет она в сцене суда, переворачивая причину и следствие. ф «Раз в парике, значит судья». (Судьи в Англии во время судебных заседаний появляются в мантиях и париках.)
В той же сцене дрожащий от страха Шляпных Дел Мастер откусывает вместо бутерброда кусок чашки, которую он держит в другой руке. Словом, «задом наперед, совсем наоборот», как сказал бы по этому поводу Траляля. Принцип этот подчеркивают наставления, которые дают Алисе участники Безумного Чаепития.
«Я говорю, что думаю, − заявляет Алиса, − и думаю, что говорю». − «Это совсем не одно и то же, − поправляют они ее. − Ведь не все равно, как сказать: «Я вижу то, что ем», или «Я ем то, что вижу», а Соня добавляет: «Так ты еще скажешь, будто «Я дышу, когда сплю», и «Я сплю, когда дышу», − одно и то же!» Л.Кэрролл разрывает привычные сочетания слов рычагом формальной логики.
«Когда тебе дурно, всегда ешь занозы, − советует Алисе Король. − Лучше средства не сыщешь!» Алиса удивлена. «Можно брызнуть холодной водой иди дать понюхать нашатырю. Это гораздо приятнее, чем занозы!» − говорит она. − «Знаю, знаю, − отвечает Король. − Но я сказал: «Лучше средства не придумаешь!» Лучше, а не приятнее».
Парадоксы Л.Кэрролла
В настоящее время термин парадокс прочно вошел в нашу речь. Его можно встретить и в научных текстах (парадоксальный сон, парадоксы природы, парадоксы науки, парадоксы творчества) и в повседневной речи («ну это уже парадокс») и художественной литературе («О сколько нам открытий чудных готовят просвещенья дух, и опыт, сын ошибок трудных, и гений, парадоксов друг»)29]. Поэтому вполне естественно, что термин парадокс понимается по-разному в разных ситуациях. В.С. Библер замечает: «Понятие парадокса существует сейчас в самых различных смыслах - от чисто словарного и повседневного (красиво звучащая бессмыслица, до строго формального (логического), наиболее осознанного в парадоксах теории множества30».
Парадокс (от др.-греч. παράδοξος − неожиданный, странный от др.-греч. παρα-δοκέω − кажусь) − истинное высказывание, утверждение, суждение или вывод, характеризующиеся парадоксальностью. Парадоксальность − неожиданность, непривычность, оригинальность, противоречивость себе, исходным посылкам, общепринятому, традиционному взгляду или здравому смыслу по содержанию и/или по форме31.
Парадокс в обще-базальном порядке
− аффирмация, которая контрастирует с общепринятыми критериями, ориентациями, установками, а также парадокс это элиминирование того, что может быть достоверным;
− неожиданное нестандартное положение, которое антитезно фактам действительности;
− дискурсивно-верное рассуждение, которое результирует харизматические тезисы, кои могут быть дискурсивно доказуемы, а уже такие положение мы не можем отнести ни к достоверным, ни к ложным;
− два антитезных утверждения, которые обладают весьма убедительными аргументациями.
Трактование парадокса как ошибки иногда приводит к тому, что его путают с другими понятиями, которые тоже обозначают ошибки, но несколько иного рода. А.В.Сухотин пишет: « Парадокс рожден в семействе понятий, описывающих ошибки и противоречия познания. Ошибки бытуют разные. Одни из них непроизвольны. Человек и не хотел бы ошибаться, да не получается. Как будто рассуждение логично, проведено правильно и, тем не менее, дает сбой»32 [9]. Другие - наоборот «делаются умышленно с намерением ввести кого-то в заблуждение»33[С.293].
С ошибками в рассуждениях приходится сталкиваться на каждом шагу, и избежать их невозможно. Больше того, процесс человеческого познания состоит, в сущности, из ошибок - в том числе ошибок в рассуждениях - и их исправления. В частности, ошибки неизбежны в спорах: если двое отстаивают противоположные мнения, то в силу закона противоречия в рассуждениях, по крайней мере, одного из них есть ошибки34[С.181].
Преднамеренные ошибки называют софизмами.
Софизм − (от греч. sóphisma − уловка, ухищрение, выдумка, головоломка) − умозаключение или рассуждение, обосновывающее какую-нибудь заведомую нелепость, абсурд или парадоксальное утверждение, противоречащее общепринятым представлениям35.
Софизм обычно определяют как умозаключение или рассуждение, обосновывающее какую-нибудь заведомую нелепость, абсурд или парадоксальное утверждение, противоречащее общепринятым представлениям. Софизмы - логически неправильные рассуждения, выдаваемые за правильные и доказательные.
Кажущаяся убедительность многих софизмов, иллюзия их «логичности» и «доказательности» связана с хорошо замаскированной ошибкой, с нарушением правил языка или логики. Софизм - это обман, но обман тонкий и закамуфлированный, так что его не сразу и не каждому удаётся раскрыть.
А.А. Ивин пишет: «В обычном и распространённом понимании софизм - это умышленный обман, основанный на нарушении правил языка и логики. Его цель - выдать ложь за истину. Считается, что прибегать к софизмам предосудительно, как и вообще обманывать и внушать ложную мысль, поэтому о софизмах обычно говорят вскользь и с очевидным осуждением36»[С.292-293]. Подобное отношение к софизмам, на первый взгляд, является вполне оправданным. Действительно, вряд ли имеет смысл задерживаться и размышлять над следующими рассуждениями, которые являются примерами софизмов:
«Сидячий встал; кто встал, тот стоит; следовательно, сидячий стоит»;
«Сократ - человек; человек - не то же самое, что Сократ; значит, Сократ - это нечто иное, чем Сократ»;
М.М. Новосёлов предлагает классификацию парадоксов, которая разделяет их на:
− парадоксы, связанные с математической индукцией (парадокс кучи, космологические парадоксы; парадокс Хао-Вана, связанный с неоднозначностью натурального ряда в аксиоматической теории множеств и формализуемостью доказательств непротиворечивости);
− парадоксы релевантности (т.е. те, в основе которых лежит допущение о возможности игнорировать подробности смысловых связей); с этими парадоксами связаны и парадоксы математической индукции, так как попытки освободиться от этих парадоксов основаны на математической индукции;
− парадоксы отождествлений (в основе которых лежит допущение о независимости тождества от отождествлений); они также связаны с парадоксами математической индукции и парадоксами актива-пассива;
− семантические парадоксы (основанные на допущение об осмысленности отношения обозначения);
− теоретико-множественные парадоксы (сводимые к предыдущим);
− парадоксы актива-пассива (отождествление происходящего с производимым и т.п.; к ним относятся парадоксы о необходимости начала мира, антиномии Канта); кроме того, из-за парадоксов актива-пассива возникают парадоксы отождествлений, а также следующие группы парадоксов:
− парадоксы модальностей, которые допускают дальнейшую классификацию: отождествление возможного с действительным, ошибка смещения целей (приводящая к тому, что достаточное считается необходимым и т.п.); пренебрежение условиями возможности (что связано с парадоксами релевантности и приводит к смешению возможности с действительностью); парадокс «утренняя звезда»
− парадоксы из-за смещения интуитивных понятий с четко определенными (они родственны семантическим парадоксам)37[С.76-77].
Парадоксы в физике были обнаружены ещё в глубокой древности. Их изучению особое внимание уделяли ученые в Древней Греции. Наиболее известными «парадоксами древней науки» являются парадоксы Зенона.
«Дихотомия» или добежит ли бегун до финиша?
Рассуждения бегуна: Прежде, чем я добегу до финиша, мне необходимо пробежать половину дистанции, затем половину оставшейся половины, то есть ¾ всей дистанции. Прежде чем я преодолею последнюю четверть дистанции, мне необходимо пробежать её половину. И так всякий раз! Прежде чем преодолеть какое-то расстояние мне необходимо пробежать его половину. Этим половинам не будет конца. Я никогда не доберусь до финиша.
В .Г.
Винокур пишет по поводу этого парадокса: «Даже сейчас, предоставив
разным компьютерам формальным образом решить парадокс Зенона, мы
убедимся, что они будут делить его до бесконечности, пока самый
"умный" из них не напишет, что задача решения не
имеет»38. На самом же деле, если
предположить, что на преодоление первой половины пути бегун
затратит 1 минуту, то каждую половину очередного отрезка он
пробегает за вдвое меньшее время, чем половину предыдущего отрезка.
Бегун преодолеет дистанцию за 2 минуты, хотя за это время ему
придется преодолеть бесконечно много половин соответствующих
отрезков дистанции.
.Г.
Винокур пишет по поводу этого парадокса: «Даже сейчас, предоставив
разным компьютерам формальным образом решить парадокс Зенона, мы
убедимся, что они будут делить его до бесконечности, пока самый
"умный" из них не напишет, что задача решения не
имеет»38. На самом же деле, если
предположить, что на преодоление первой половины пути бегун
затратит 1 минуту, то каждую половину очередного отрезка он
пробегает за вдвое меньшее время, чем половину предыдущего отрезка.
Бегун преодолеет дистанцию за 2 минуты, хотя за это время ему
придется преодолеть бесконечно много половин соответствующих
отрезков дистанции.
Быстроногий Ахилл хочет поймать черепаху, которая находится на расстоянии 1 км от него.
К тому времени, когда Ахилл добегает до того места, где первоначально находилась черепаха, та успевает уползти вперёд на 10 м. За то время, которое требуется Ахиллу, чтобы пробежать эти 10 м, черепаха снова успевает уползти на какое-то расстояние. И так далее пока Ахилл будет приближаться к черепахе, та всё равно успеет уползти на какое-то расстояние вперёд, хоть на толщину волоса! И все-таки, Ахилл мог поймать черепаху.
Парадоксы Зенона показывают, к каким парадоксальным следствиям приводит представление о неделимых - «атомах» - пространства и времени, имеющих сколь угодно малые, но конечные размеры39.
В главе «История Рыбного Деликатеса» Алиса получает урок классической философии наоборот. Ей снится известный в то время школьный парадокс о неуязвимом Ахиллесе и черепахе. Ахиллес бегает быстрее черепахи, но черепаха, тем не менее, всегда впереди, так как всегда ближе к точке старта. Алиса появляется как свидетель «третий», которому два существа, классически медленное и классически быстрое, дают урок «тише едешь − дальше будешь». Л. Кэрролл дополняет его собственным выводом − бег «от» и «к» приводит к убыванию времени. Борхес назвал это открытие Л. Кэрролла «бесконечным рядом убывающих расстояний».
«К парадоксам следует воспитывать в себе особые симпатии. Ведь в них обнажаются «горячие точки» науки, пункты ее наиболее вероятных продвижений вперед»40. Следовательно, парадоксы - это скорее полезное явление, а не вредное (как принято считать). Они полезны для науки в целом и, особенно, для её развития, продвижения вперед.
Чеширский кот
…Кот исчез - на этот раз очень медленно. Первым исчез кончик его хвоста, а последней - улыбка; она долго парила в воздухе.
− Д-да! - подумала Алиса, - Видела я котов без улыбок, но улыбка без кота! Такого я в жизни ещё не встречала…
Выражение «улыбка без кота» представляет собой неплохое описание чистой математики, хотя математические теоремы часто могут быть успешно приложены к описанию внешнего мира, сами теоремы суть абстракции гения, принадлежащие другому царству, «далекому от человеческих страстей».
Оксфордская радость доктора Доджсона, любовь его ночей бессонных - «чистая математика», помещена в книжку в образе Чеширского Кота (Cheshire Cat). Привлекательная гармония чистой науки управляет хаосом, как Чеширский Кот своей зримостью. Растворяясь по собственной надобности, кот оставляет взамен лишь чистый знак.
Ч еширский
Кот − постоянно ухмыляющееся существо, умеющее по собственному
желанию постепенно растворяться в воздухе, оставляя на прощанье
лишь улыбку…− является одним из основных персонажей книги.
Занимающий Алису не только забавляющими её разговорами, но и порой
чересчур досаждающими философскими измышлениями…
еширский
Кот − постоянно ухмыляющееся существо, умеющее по собственному
желанию постепенно растворяться в воздухе, оставляя на прощанье
лишь улыбку…− является одним из основных персонажей книги.
Занимающий Алису не только забавляющими её разговорами, но и порой
чересчур досаждающими философскими измышлениями…
В первоначальном варианте книги Льюиса Л. Кэрролла Чеширский Кот как таковой отсутствовал. Появился он только в 1865 году.
Именно с этого момента кот постоянно сопровождает Алису, делится с ней весьма пространными размышлениями и также внезапно исчезает, как и появляется. И лишь только висящая в воздухе улыбка напоминает об этом необычном животном.
Алиса знакомится с Чеширским Котом.
…Только кухарка не чихала, да ещё - огромный кот, что сидел у печи и улыбался до ушей.
− Скажите, пожалуйста, почему ваш кот так
улыбается? - спросила Алиса робко.
− Потому, - сказала Герцогиня. − Это Чеширский Кот, - вот почему!..
В те времена часто использовалось выражение − «улыбается, как чеширский кот». Эта поговорка стала предметом многочисленных споров в университете Оксфорда. Выдвигалось много гипотез насчет ее происхождения и подробного значения.
В «Книге Вымышленных Существ», в разделе «Чеширский кот и коты из Килькеннии» (The Cheshire Cat and the Killkenny Cats), Борхес пишет: «В английском языке есть выражение «grin like a Cheshire cat» (сардонически усмехаться, как чеширский кот). Предлагаются разные объяснения. Одно состоит в том, что в Чешире продавали сыры, похожие на голову улыбающегося кота.
Эта теория имеет интересные абсурдные последствия, так как сырный кот может быть, в таком, случае быть съеден мышью! Или - если мы допускаем существование чеширского кота как породы - он может съесть мышь, которая съела его в виде сыра!
Второе − что над высоким званием небольшого графства Чешир «смеялись даже коты».
Д октор
Доджсон родом из чеширских мест. Коты там особенной масти − шерсть
цвета персика, хватка − тигриная.
октор
Доджсон родом из чеширских мест. Коты там особенной масти − шерсть
цвета персика, хватка − тигриная.
Другие считают, что кошки были завсегдатаями вывесок различных чеширских харчевен. Они изображались в различных ракурсах − могли спокойно сидеть, могли вальяжно лежать, а могли и улыбаться. Вероятно, изначально эти бесхитростные вывески претендовали на изображение свирепых леопардов или львов, угрожающе скалящих пасть. Но история и наблюдательный человеческий глаз все расставили на свои места.
Если присмотреться, кошечки на вывесках невероятно похожи на важную и уравновешенную британскую породу. Представители британской кошачьей разновидности по природе своей обладают очень большими щеками. На них хорошо заметны подушечки для усов, «смотрящие» в разные стороны. Благодаря ним, создается впечатление, что кошка хитровато ухмыляется чему-то.
Эта интересная особенность внешнего вида британских кошек была сразу же замечена острым взглядом англичан. И с давних пор существует «grin - народная английская поговорка − «улыбаться, как чеширский кот» like a Cheshire cat».
Когда молодой Доджсон приехал в Оксфорд, там как раз шла дискуссия о происхождении этой поговорки. Доджсон, уроженец Чешира, не мог ей не заинтересоваться.
Доктор Доджсон, автор «Математических курьезов» и «Символической логики», преподнес в подарок Алисе кота высокого интеллекта − загадку на убывание. Знаменитая улыбка Чеширского кота − она продолжает висеть в воздухе, даже, когда кот исчезает. И до сих пор не установлено, почему Чеширский кот улыбается именно так.
Чеширский Кот обладает способностью появляться и исчезать по частям. Когда он появлялся, то первой появлялась его улыбка, а когда он исчезал - она исчезала последней.
С одной стороны, улыбка чеширского кота воспринимается как нечто реально осязаемое и понятное, вполне сенсорное, но, с другой − есть в ней какая-то мистическая неуловимость и самостоятельность. Подобно этому существуют и многие математические понятия − мы не сомневаемся в их реальности, мы умеем с ними работать, мы научились с определенной степенью достоверности распознавать и идентифицировать их, мы видим какие-то их признаки и проявления, но они непосредственно не фиксируются. Во все большей и большей степени становится ясным, что эти понятия выводят нас на ту грань, за которой рациональный человеческий интеллект становится бессильным. Улыбка Чеширского Кота стала символом современной математики.
«Да! - подумала Алиса. - Видала я котов без улыбок, но улыбка без кота! Такого я в жизни еще не встречала».
Помимо очевидного обыгрывания примера невозможности в некоторых ситуациях применить обратную логику (как, например, в таком выражении: «все шоферы - люди, но не все люди - шоферы» и т.д.), Л. Кэрролл в этом парадоксе метафорически описывает суть чистой математики. Понятно, что математические теоремы и измышления могут быть успешно применены к описанию внешнего мира, хотя, по сути, они - не более чем абстракции гения. В известном смысле, математика и есть «улыбка без кота». То есть, по словам Бертран Рассела, «чистая мысль».
Кэрролловская арифметика в сказках об Алисе
Операция умножения
«Как все непонятно! А ну-ка, проверю, помню ли я то, что знала. Значит так: четырежды пять - двенадцать, четырежды шесть - тринадцать, четырежды семь… Так я до двадцать никогда не дойду!»
Как известно, в силу традиции в Англии долгая время использовалась двенадцатиричная система исчисления (например, мер и денежных единиц). По этой же причине в Англии дети учат таблицу умножения до 12 (а не до 10 как у нас). Получается, что, действительно, эта абсурдная последовательность закончится на 19:
4 × 7 = 14
× 7 = 14
4 × 8 = 15
4 × 9 = 16
4 × 10 = 17
4 × 11 = 18
4 × 12 = 19
Хотя один из комментаторов - А.Л. Тейлор - предлагают куда более интересное объяснение этой сентенции Алисы. Так, если за основание системы исчисления принять 18 (то есть использовать восемнадцатиричную систему исчисления вместо привычной для нас десятиричной), то равенство 4 × 5=12 будет верным. Далее, если мы будем постоянно менять основание, увеличивая его на 3, то произведения будут последовательно увеличиваться на единицу: в системе с основанием 21: 4×6=13, с основанием 24: 4×7=14 и т.д. И так до основания 42 и, соответственно, множителя 13. При данном основании 4×13=1, а не 20. То есть, следуя этой замысловатой логике, Алиса и вправду не сможет дойти до 20.
Операция деления
Из арифметики хорошо известна операция деления чисел. Деление понятий, или логическое деление, - другая мыслительная операция, имеющая с первой общие не только название, но и структуру: у обеих операций есть «делимое», «делитель» и «результат деления». Логическое деление применяется к понятиям, результат такого деления - несколько новых, видовых понятий. В содержание последних входят все те признаки, которые мыслились в исходном, родовом понятии, и, кроме того, признаки, отличающие один вид от другого.
Логическое деление, случается, смешивают с другой операцией, которая тоже иногда именуется «делением», - с расчленением некоторого предмета на составные части.
Слово «деление» употребляется и в других смыслах. Они связаны с основными только посредством зыбких сиюминутных ассоциаций.
В сказке Л.Л. Кэрролла Белая Королева спрашивает Алису, знает ли она
арифметическую операцию деления:
сказке Л.Л. Кэрролла Белая Королева спрашивает Алису, знает ли она
арифметическую операцию деления:
«− Раздели буханку хлеба ножом − что будет?
− По-моему... − начала Алиса, но тут вмешалась Черная Королева.
− Бутерброды, конечно, − сказала она. − А вот еще пример на вычитание. Отними у собаки кость − что останется?
Алиса задумалась.
− Кость, конечно, не останется − ведь я ее отняла. И собака тоже не останется − она побежит за мной, чтобы меня укусить... Ну и я, конечно, тоже не останусь!
− Значит, по-твоему, ничего не останется? − спросила Черная Королева.
− Должно быть, ничего...»
Такого рода комические «деления» и «вычитания» даже при желании не спутаешь с обычными операциями над числами и понятиями.
Фантазии Л. Кэрролла и информатика
Ответьте простой вопрос: а что такое компьютер?
Далеко не каждый так вот с ходу запросто может дать определение, отражающее главные свойства компьютера, тем более что собственно и само название сбивает с толку. В самом деле, и русское вышедшее из употребления название "электронно-вычислительная машина", и английское "компьютер", которое, собственно, переводится на русский точно так же − "вычислитель", − говорят о первоначальном главном предназначении этих устройств − решать математические задачи.
Изучив информатику мы знаем, как именно компьютер выполняет расчеты: все расчеты, которые выполняет компьютер, в конечном итоге базируются всего на одной операции − сложении. Компьютерное вычитание − это сложение уменьшаемого с дополнительным кодом вычитаемого. Компьютерное умножение − это более сложная операция в виде циклического сложения первого множителя с самим собой, "сдвигаемым влево" на каждом шаге цикла, согласно битовой маске второго множителя. Наконец, деление − это циклическая комбинация умножений и вычитаний, то есть, в конечном итоге, все тех же сложений. А степени, корни и прочее − это более сложные операции, базирующиеся на умножении, делении и т. д. Короче, все дороги ведут в Рим, а все компьютерные математические операции апеллируют к сложению.
Компьютер, а вернее арифметико-логическое устройство (АЛУ) его центрального процессора, также "знает" несколько аксиом, на которых и держится вся эта хитрая штука с трехмерными играми, стереозвуком, видеопроигрывателями и прочим. Вот эти аксиомы: 0 + 0 = = 0; 0 + 1 = 1; 1 + 0 = 1; 1 + 1 = 0.
Когда АЛУ процессора выполняет побитовое сложение разрядов двух чисел, то в случае если в обоих разрядах стоят единицы, схемы АЛУ устанавливают соответствующий разряд итогового числа в ноль (четвертая аксиома) и вырабатывают сигнал переноса разряда, который будет учитываться при сложении следующих двух битов. Получается, что при побитовом сложении схемы АЛУ всякий раз (кроме сложения самых младших разрядов) складывают не два, а три бита (третий − это возможная единица переноса, образовавшаяся при сложении предыдущего разряда). А ведь сложение − это, как было уже сказано выше, самая массовая математическая операция.
И представьте, насколько бы увеличилась производительность компьютеров, если бы они оперировали не двумя числами, а тремя. Таким образом, мы незаметно подошли к идее троичного компьютера.
На пути создания троичного компьютера имеется ряд ограничений; первое − элементное. Основа оперативной памяти (и внутренних схем процессора) современных компьютеров − триггеры. Триггер, или защелка, − это электронное устройство, которое всегда может находиться лишь в одном из двух состояний, которые интерпретируются либо как ноль, либо как единица. Стало быть, на триггерах троичный компьютер не построишь, ведь нужно, чтобы первичный элемент находился в одном из трех состояний. Однако элементные ограничения − это не самая большая сложность. Еще большая сложность − это логика компьютера.
Современные компьютеры − это логические машины. Большая часть операций, которые выполняются в них, − не математические, а логические. Да, собственно, и четыре аксиомы АЛУ − это не математика, а логика. В самом деле, эти аксиомы логически расписываются следующим образом: "если первый бит равен 0, а второй равен 1, то в ответе − 1" и т. п. Это булева логика, введенная в 1847 году английским математиком Джорджем Булем (см. статью "Паро-вычислительная машина Бэббиджа", Upgrade # 1 (91)). Булева логика − двоичная, она очень и очень подходит двоичным машинам, но для троичных машин и логика должна быть троичной. А где ее взять? И вот тут мы снова возвращаемся к автору "Алисы в стране чудес".
В 25 лет Чарльз Лутвайдж Доджсон (Льюис Л. Кэрролл) получил степень магистра математики, все его наиболее значимые работы (известные в основном специалистам) были посвящены математической логике и разработке силлогистики − науки, основателем которой считается Аристотель. В своей работе "Символическая логика" Л. Кэрролл рассмотрел вопросы классификации объектов и их признаков, а также ввел бинарные и троичные диаграммы, позволяющие формализовать любые суждения. Строго говоря, Льюис Л. Кэрролл в середине XIX века (как раз тогда, когда Дж. Буль опубликовал свою работу "Математический анализ логики") разработал теорию построения логических автоматов, хотя ни о каких автоматах он и не задумывался. В своей работе Л. Кэрролл предложил специальные диаграммы для представления в простой форме (квадраты, разбитые на клетки, и фишки черного и белого цвета) различных логических суждений.
Пятая книга "Символической логики" Л. Кэрролла посвящена силлогизмам и является дальнейшим развитием идей Аристотеля. Очень упрощенно можно сказать, что эта книга стала во многом основой науки силлогистики, которая, в противовес логике двоичных суждений, предвосхитила троичную логику. Силлогистика Л. Кэрролла была успешной попыткой преодоления "нестыковок" материальной импликации (смотрите врезку "Импликация"). По мнению некоторых исследователей, Льюис Л. Кэрролл под видом детской сказки попытался внедрить свои открытия в области математической логики.
Но литературный талант сыграл с ним злую шутку. "Алиса в стране чудес" покорила весь цивилизованный мир… но лишь как забавная, искрометная, полная странных каламбуров сказка. Не зная его научных работ, "Алису" можно воспринимать только как совершенно алогичную книгу − увы, открытия Л. Кэрролла в области логики остались в основном незамеченными. Сегодня ни в одном учебнике по логике (классической или математической) не упоминается ни имя Льюиса Л. Кэрролла, ни его работа "Символическая логика".
Итак, как же ответить на вопрос о том, имеет ли отношение к истории вычислительной техники автор "Алисы в стране чудес"? Если бы все дело закончилось простым забвением его математических работ, то, видимо, ответ должен быть отрицательным. Но все дело в том, что его "Символическая логика" повлияла на русского инженера и изобретателя Н. П. Брусенцова, который в конце 50-х годов прошлого века сконструировал в МГУ и запустил в серию единственную в мире ЭВМ с троичной архитектурой. У Брусенцова даже есть работа, которая называется "Диаграммы Льюиса Л. Кэрролла и аристотелева силлогистика"41.
Таким образом, логика Л.Л. Кэрролла, действительно, оказывается логикой, не зависящей в своих законах и семантике от знания о мире, его структуре и т.д. Она предстает действенным инструментом познания, а не учением о структуре мира, как это явно или неявно получается в традиционном экстенсионально ориентированном логицизме. Начиная со всех возможных (иногда весьма экзотических, «лишенных смысла») комбинаций терминов, вроде бы - с чисто словесной, «безответственной» игры, мы получаем возможность строгого анализа информации, чтобы с учетом достоверного знания, полученного опытным путем, получать новое знание.
Нонсенс действительно оказывается необходимым условием истины.
Глава II. Геометрия и физика Л. Кэрролла
Мысли о свободном падении
В первой главе Алиса попадает в Страну Чудес.
Алиса юркнула за Кроликом следом. Нора шла сначала прямо, ровная, как туннель, а потом вдруг круто оборвалась вниз…

Илл. Millicent Sowerby (1907)
Она всё падала и падала. Неужели этому не будет конца? А не промчу ли я всю землю насквозь? Вот будет смешно. Вылезаю, а люди все вниз головой! Как их зовут? Антипатии, кажется…
В о
времена Л.Л. Кэрролла высказывались различные догадки о том, что
случиться, если упасть в туннель, проходящий через центр Земли.
Этот вопрос задал ещё Плутарх. Правильный ответ дал
Г.Галилей42: тело будет падать с возрастающей
скоростью, но с убывающим ускорением, пока не достигнет центра
Земли, где ускорение равно нулю. После этого скорость его станет
уменьшаться, а замедление - увеличиваться до тех пор, пока тело не
достигнет противоположного конца туннеля. Затем снова начнется
падение к центру Земли. Если пренебречь сопротивлением воздуха и
силой Корнолиса. Возникающей вследствие вращения Земли, то можно
считать, что тело будет колебаться вечно. Сопротивление воздуха,
разумеется, в конце концов, остановит его в центре Земли.
о
времена Л.Л. Кэрролла высказывались различные догадки о том, что
случиться, если упасть в туннель, проходящий через центр Земли.
Этот вопрос задал ещё Плутарх. Правильный ответ дал
Г.Галилей42: тело будет падать с возрастающей
скоростью, но с убывающим ускорением, пока не достигнет центра
Земли, где ускорение равно нулю. После этого скорость его станет
уменьшаться, а замедление - увеличиваться до тех пор, пока тело не
достигнет противоположного конца туннеля. Затем снова начнется
падение к центру Земли. Если пренебречь сопротивлением воздуха и
силой Корнолиса. Возникающей вследствие вращения Земли, то можно
считать, что тело будет колебаться вечно. Сопротивление воздуха,
разумеется, в конце концов, остановит его в центре Земли.
На интерес Л. Кэрролла к этой проблеме указывает и тот факт, что в его романе «Сильви и Бруно» (гл. 7) немецкий профессор описывает наряду с листом Мебиуса, проективной плоскостью и другими научными и математическими диковинками чудесный метод, с помощью которого можно приводить поезда в движение одной лишь силой тяжести. Рельсы следует проложить в совершенно прямом, прорытом по хорде, туннеле, который соединит два города. Середина туннеля, естественно, находится ближе к центру Земли, чем концы, вследствие чего поезд будет скатываться «под гору» к центру, приобретая при этом достаточный разгон, который вынесет его к другому концу. Любопытно, что поезд пройдет нужное расстояние (если не принимать во внимание сопротивление воздуха и трение колес) за время, в точности равное периоду колебания предмета, падающего в туннеле, прорытом по диаметру Земли, а именно: немногим более 42 минут. Это время не зависит от длины туннеля.
«Не успела Алиса и глазом моргнуть, как она начала падать, словно в глубокий колодец. < … > Пролетая мимо одной из полок, она прихватила с нее банку с вареньем. На банке было написано «Апельсиновое», но увы! она оказалась пустой. Алиса побоялась бросить банку вниз - как бы не убить кого-нибудь! На лету она умудрилась засунуть ее в какой-то шкаф».
Этим пассажем Л. Кэрролл, очевидно, заставляет читателя задуматься над абсурдностью описанной ситуации. Как вы понимаете, Алисе совсем не нужно было бояться бросить банку с вареньем вниз, так как в условиях свободного падения, банка бы никуда не упала - она осталась бы перед ней в подвешенном состоянии. Естественно, что и поставить банку на полку Алиса тоже никак не смогла бы, так как скорость падения была бы слишком большой. Как это ни удивительно, но именно такие размышления позволили Эйнштейну сформулировать специальную теорию относительности: «для наблюдателя, свободно падающего с крыши, гравитационное поле, по крайней мере, в его ближайшем окружении, не существует. В самом деле, если при этом наблюдатель бросает какие-то предметы, то они находятся по отношению к нему в состоянии покоя или равномерного движения вне зависимости от их физического или химического состава... В распоряжении наблюдателя нет объективных средств обнаружения своего падения в гравитационном поле. В таком случае он вправе считать, что находится в покое в пространстве, лишенном поля тяготения». И далее Эйнштейн описывает знаменитый эксперимент с падающим лифтом: «Вообразите в космосе лифт, движущийся вверх с постоянно нарастающей скоростью. Если ускорение постоянно и в точности равно ускорению падающего на Землю предмета, то человек внутри лифта будет себя чувствовать, как на Земле, - таким путем можно не только смоделировать тяготение, но и нейтрализовать его. В падающем же лифте ускорение вниз полностью ликвидирует влияние тяготения».
Свойства окружности
Вспомним эпизоды, где идёт речь о свойствах окружности.
В огромную лужу слёз, которую наплакала Алиса, попáдали разные птицы и звери. Выбравшись из лужи, они стали искать способ, как побыстрее обсохнуть. По предложению Птицы Додо было решено устроить бег по кругу.
«Сначала он нарисовал на земле круг. Правда, круг вышел не очень-то ровным, но Додо сказал:
− Правильность
формы несущественна!
Правильность
формы несущественна!
А потом расставил всех без всякого порядка по кругу. Никто не подавал команды − все побежали, когда захотели… Через полчаса, когда все набегались и просохли, Додо вдруг закричал:
− Бег закончен! Все столпились вокруг него и, тяжело дыша, стали спрашивать:
− Кто же победил?
На этот вопрос Додо не мог ответить, не подумав
как следует… Наконец, Додо произнёс:
− Победили все! И каждый получит награды!»
Математиков в этой истории могли бы заинтересовать три момента.
Во-первых, почему Додо расставил всех по кругу без всякого порядка? Почему бы для точек круга, а вернее окружности, не указать, какая из трёх произвольно взятых точек находится между двумя другими (по аналогии с точками прямой)? Если хотите, имеет ли смысл это делать?
Во-вторых, что именно заставило Додо как следует задуматься? Иначе говоря, почему в беге по кругу не оказалось проигравших, а были одни победители?
И, наконец, что имел в виду Додо, сказав о нарисованной на земле линии: «Правильность формы несущественна»?
О каких свойствах окружности поведал нам автор - математик Чарлз Лютвидж Доджсон, предстающий в этом эпизоде в образе Птицы Додо?
Для точек окружности нет смысла указывать, какие из них лежат между другими. Можно сказать, они равноправны, как и точки всякой плоской простой (без самопересечений) замкнутой кривой. «Правильность формы несущественна», как выразился Додо. А если учесть, что участники начали бег, когда захотели, да ещё из разных точек, Додо действительно было о чём призадуматься. Он принял мудрое решение, объявив победителями всех.
Когда Алиса повстречалась с Синей Гусеницей (та восседала на огромном, ростом с девочку, грибе и томно курила кальян), между ними завязалась беседа, в ходе которой девочка пожаловалась на свой маленький рост.
«− Если вы не возражаете, сударыня, − отвечала Алиса, − мне бы хотелось хоть капельку подрасти. Три дюйма − такой ужасный рост!
− Со временем привыкнешь, − возразила Гусеница, сунула кальян в рот и выпустила дым в воздух.
А лиса
терпеливо ждала, пока Гусеница не соблаговолит снова обратить на
неё внимание. Минуты через две та вынула кальян изо рта, зевнула −
раз, другой − и потянулась. Потом она сползла с гриба и скрылась в
траве, бросив Алисе на прощанье:
лиса
терпеливо ждала, пока Гусеница не соблаговолит снова обратить на
неё внимание. Минуты через две та вынула кальян изо рта, зевнула −
раз, другой − и потянулась. Потом она сползла с гриба и скрылась в
траве, бросив Алисе на прощанье:
− Откусишь с одной стороны − подрастёшь, с другой − уменьшишься!
− С одной стороны чего? − подумала Алиса. − С другой стороны чего?
− Гриба, − ответила Гусеница, словно услышав вопрос, и исчезла из виду.
С минуту Алиса задумчиво смотрела на гриб, пытаясь определить, где у него одна сторона, а где − другая; гриб был круглый, и это совсем сбило её с толку».
Да уж, есть о чём призадуматься!
Если бы Алиса была знакома со свойствами окружности, то не тратила бы время зря, пытаясь определить, где у гриба одна сторона, а где другая. У круглого гриба вообще нет сторон!
− Ну вот, голова, наконец, освободилась! − радостно воскликнула Алиса. Впрочем, радость ее тут же сменилась тревогой: куда-то пропали плечи. Она взглянула вниз, но увидела только шею невероятной длины, которая возвышалась, словно огромный шест, над зеленым морем листвы.
− Что это за зелень? − промолвила Алиса. − И куда девались мои плечи? Бедные мои ручки, где вы? Почему я вас не вижу?
С этими словами она пошевелила руками, но увидеть их все равно не смогла, только по листве далеко внизу прошел шелест».43
Идеализация пространства
Каждый поворот сюжета, каждое слово Сказки и каждый поступок Льюиса Кэрролла и Алисы Лидделл скрупулёзно изучены лириками и физиками. Образы Кэрролла получили независимое существование, а аллегории - самое различное толкование: политическое, психологическое, психоаналитическое, богословское, логическое, математическое, физическое, филологическое.
Незамеченным для исследователей оказалось лишь то, что лежит на виду - ПРОСТРАНСТВО СКАЗКИ. При этом все знали, что Сказку писал преподаватель математики. Первое её издание состоялось в 1865 году, а в 1854 году другой преподаватель математики Бернгард Риман говорил о «n-мерных пространствах». Само же выражение «четвёртое измерение» (quarta dimensio) появилось в Англии в 1671 г.
Мы изучаем геометрию Евклида-Гильберта и, соответственно, взираем на мир через евклидово пространство.
В качестве основных характеристик евклидова пространства выделяют следующие:
«оно бесконечно; оно беспредельно; оно однородно; оно изотропно; оно связно; оно однозначно; оно трехмерно; оно имеет постоянную кривизну, равную нулю».44
Однако, пространство евклидовой геометрии не является единственно возможным в геометрической действительности. Более того, что в основе других теоретических действительностей (например, физической действительности) может лежать совсем другая идеализация пространства. И данный пример с грибом из Л. Кэрролловской «страны чудес», которая построена как раз на неевклидовом пространстве, позволяет нам решать данные задачи.
Прибытие Алисы в мир малых измерений (страну чудес) происходит не одномоментно. Сначала - свободное падение в Кроличьей Норе, с утратой физических констант: плавное уменьшение тяготения и отрицательная инерционность, потом измененная стационарность внешнего мира и утрата линейного восприятия времени. В геометрии нет «верха - низа», нет гравитационной информации, нет времени. Движение, вращение и совмещение фигур в геометрии возможно.
Иными словами, Алиса посредством морфологических и геометрических трансформаций из реальности физической (пикник на берегу Темзы 4 июля 1862 года) оказывается в иной «виртуальной реальности», где господствующее положение принадлежит двумерцам - игральным картам.
Остальные жители этого мира, возможно, такие же переселенцы, как и Алиса, обладают изысканным литературным английским языком, протологикой и метаязыком. Квазиобитатели, как и КвазиАлиса, имеют изменённые инстинкты, пропорции и размеры - последствия преобразований. Трансформации Алисы и Чеширского Кота - вторая пространственная идея Сказки.
Обитатели «страны чудес» воспринимают Alise не как часть своего мира, а как пришельца, до которого им нет никакого дела. Они заняты своими двумерными страстями. Им заметны в ней трёхмерные странности, как и в четырёхмерном КвазиЧешике. Но им не понять, что их Высокие гости обладают «пространственной независимостью» и даже - «пространственной безопасностью».
- А ещё я хотела подняться на вершину холма…
- Разве это холм? - перебила её Королева - Видала я такие холмы, рядом с которым этот - просто равнина!
- Ну, нет! - сказала вдруг Алиса, и сама удивилась, как это она решается возражать Королеве. - Холм никак не может
быть равниной. Это уж совсем чепуха!
- Разве это чепуха? - сказала Королева и затрясла головой. -
Слыхала я такую чепуху, рядом с которой эта разумна, как толковый словарь!
Крупнейший физик ХХ века Артур Стэнли Эддингтон, цитируя эти слова Черной Королевы, утверждает, что, хотя физику, возможно, бессмысленно утверждать, что существует какая-то иная реальность, помимо той, которая подвластна законам физики, всё же это осмысленно, как толковый словарь, по сравнению с бессмыслицей предположения, что этой реальности вовсе не существует.
А как все-таки в реальности − здесь, а не в Стране Чудес − устроено пространство? Оно однородно или неоднородно? Можно ли найти такую теоретическую действительность, в рамках которой поляризованный гриб был бы возможен? Разные тексты начитывались, но таких действительностей не обнаруживалось.
Какая идеализация пространства лежит в основе оптики, классической механики и электромагнетизме, является ли там пространство однородным или неоднородным и построить модель объяснения устройства гриба, исходя из данного пространства?
Впервые задумываешься над тем, каково же оно «на самом деле», насколько пространство из евклидовой геометрии применимо ко всем случаям познания мира45, насколько оно совпадает с тем, которое выстраивается внутри физики, биологии, географии и т.д.?
Вторая сказка Кэрролла «Сквозь Зеркало и что там увидела Алиса, или Алиса в Зазеркалье» более лиричная, многоплановая и многомерная. Взаимоотношениям героев Зазеркалья за 130 лет посвящены многочисленные исследования. Предметом нашего интереса являются пространственные и отражённые повороты сюжета.
Поскольку геометрические аспекты были усилены парадоксами зеркальных отражений, можно только удивляться предвидению Кэрроллом будущего значения понятия симметрии, как фундаментального научного направления.
Силовое поле «Звёздных Врат» в телевизионных сериалах, словно гигантское зеркало, покрылось сверкающей рябью и, шагнувшие в Зазеркалье американские десантники, стали исчезать один за другим, чтобы нести демократию и права человека в другие миры и измерения.
Схематизация времени
Д ругим,
не менее знаменитым и завораживающим детское внимание эпизодом в
«Алисе…» является эпизод, известный под названием «Безумное
чаепитие».
ругим,
не менее знаменитым и завораживающим детское внимание эпизодом в
«Алисе…» является эпизод, известный под названием «Безумное
чаепитие».
«…С тех пор, − продолжал грустно Болванщик, − Время для меня палец о палец не ударит. И на часах все время шесть…
Тут Алису осенило.
-
Поэтому здесь и накрыто к чаю? − спросила она.
-
Да, − отвечал Болванщик со вздохом. − Здесь всегда пора пить чай. Мы не успеваем даже посуду вымыть.
-
И просто пересаживаетесь, да? - догадалась Алиса.
-
Совершенно верно, − сказал Болванщик. − Выпьем чашку и пересядем к следующей.
-
А когда дойдете до конца, тогда что? − рискнула спросить Алиса.
-
А что, если мы переменим тему? − спросил Мартовский Заяц и широко зевнул…»46
Этот эпизод интересен тем, что он позволяет обратиться к формированию у учащихся идеализации времени - опять же через обсуждение его свойств.
Ясно, что остановка часов не есть остановка времени. «Часы остановить можно, а время нет».
Что такое для нас есть время
В ответ на этот вопрос пишут формулу: ![]() .
.
Обращение же к «Безумному чаепитию» и разыгрывание всякого рода мыслительных экспериментов по поводу него позволяет это сделать.
Организуя мыслительный эксперимент, вместе с Алисой, Мартовским Зайцем, Болванщиком и Мышью-Соней мысленно сядем за стол: в каком времени мы сейчас «живем» - в линейном или циклическом? Можно ли утверждать, что в линейном времени? Ведь двигаясь только вокруг стола и все время возвращаясь к «исходному» стулу, мы никуда в конечном счете не перемещаемся? А раз перемещения нет, то нет и времени47. Но можно ли, в свою очередь, утверждать, что мы живем в циклическом времени? Как в этом случае фиксировать ход времени?
Если сидеть за столом бесконечно долго, без часов, никуда не выходя и осуществляя только процесс чаепития?.. Остановится ли в этом случае время? Какое именно? Циклическое? Значит, начнется линейное? Но ведь герои по-прежнему не будут совершать никакого перемещения в пространстве…
Реконструировав и промыслив ту модель, которая на самом деле была положена математиком Л. Кэрроллом в основу веселого эпизода: что будет, если свести вместе линейное и циклическое время? Не произойдет ли его «остановки»? Не исчезнет ли вообще время? Или же мы окажемся лишь в новой эпистемической ситуации, когда обе модели (линейного и циклического времени) будут взаимно проблематизированы и нам необходимо будет построить какую-то новую, абсолютно другую и никому ранее не известную модель, действительно объясняющую феномен времени?
Как, например, зарисовать остановленное время? Можно ли его зафиксировать с помощью точки?
Что означает точка − момент «пустоты» во времени? Но возможен ли такой «момент», когда нет никакого момента − «пустота»?.. Или же точка означает момент длительности? Тогда это не остановка.
Можно ли остановленное время нарисовать как ствол срубленного дерева - в виде огромного-преогромного пня, у которого много-много колец?
Чем тогда остановленное время отличается от вечности? Остановленное время - это все, что было, и все, что будет? Т.е. это − все моменты, взятые одновременно? Или же наоборот, это − полное отсутствие времени?..
А календарь − чем он как модель времени отличается от модели-«пня»?

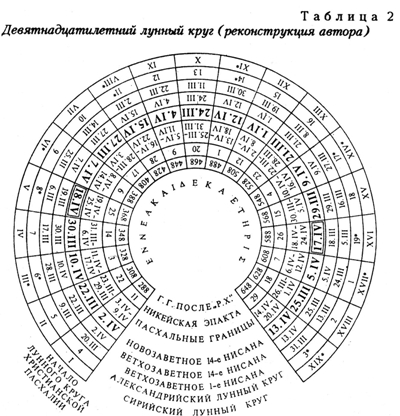
Схема «Конструктивные принципы древнерусского календаря»
Не означает ли сам календарь остановку времени? Ведь он изображает постоянное повторение одного и того же − лета, осени, зимы, весны… Подобно тому, как Болванщик, Мартовский Заяц и Мышь-Соня пересаживаются на одни и те же стулья вокруг одно и того же стола, так и времена года «пересаживаются» одно на место другого. Не есть ли это постоянное, монотонное повторение сезонов года − остановка времени?.. А что, если нарисовать календарь всех тысячелетий, которые уже прошли и которые наступят? Что такой календарь будет означать? Вечность? Полноту времени? Множество всех возможных времен? Или просто бесконечное повторение? А бесконечное повторение − это и будет остановленное время? Пустота? Или это все-таки будет вечность?..
На схеме из книги А.Н. Зелинского «Конструктивные принципы древнерусского календаря» изображена модель Великого миротворного круга, которая представляет собой не только «сконцентрированное выражение основных принципов древнерусского календаря, но и является частью средневековой концепции мира вообще.
Она охватывает в сложном единстве все основные аспекты времени в средневековом понимании последнего − а) космический, б) исторический, в) литургический»48. Таким образом, данная модель может быть рассмотрена как схема всевозможных календарных схем или как модель «полноты времен».
«Какие смешные часы! - заметила Алиса. - Они показывают число, а не час!».
Тут будет уместно вспомнить один замечательный парадокс, придуманный Л. Кэрроллом. А заключается он в следующем: часы, которые совсем не ходят, тем не менее, более точны, чем часы, которые отстают или спешат. Л. Кэрролл объяснял это тем, что в первом случае часы показывают верное время целых два раза в день, а вторые - ни разу. И ведь это абсолютная правда!
« … и на часах все время шесть.
− Поэтому здесь всегда накрыто к чаю? - спросила Алиса».
Как вы помните, безумное чаепитие в сказке Л. Кэрролла было вечным в связи с тем, что часы Болванщика остановились и все время показывали шесть (тогда в Англии чай пили в шесть, а не в пять, как сейчас).
Довольно интересно эта ситуация связывается с появившейся несколько позднее (а именно, в 1917 году) теорией вселенной голландского астронома де Ситтера. Так вот, он разработал модель, в которой время искривлялось так же, как и пространство. Вылетев из одной точки пространства и выдерживая прямой линию полета, путешественник должен был возвратиться не только в ту же точку пространства, но и в то же самое время! Согласно теории де Ситтера, чем дальше взгляд земного наблюдателя проникал в пространство, тем медленнее должны были ему казаться происходящие там процессы. Стоило же предпринять путешествие «в эти отдаленные области лени и неторопливости» на космическом корабле, как по мере нашего приближения мы увидели бы постепенное оживление хода времени. И к моменту нашего прибытия жизнь кипела бы там в обычном темпе.
Вот так Л. Кэрролл предвосхитил революционные теории пространства и времени.
Зеркальная симметрия
Ряд эпизодов из сказки «Алиса в Зазеркалье» иллюстрирует идею зеркальной симметрии.
Зеркала… Загадочные предметы, без которых не представима жизнь человека. Зачем человеку нужно зеркало? Почему каждый с таким упорством вглядывается в свое отражение? Только ли это прихоть, или в желании увидеть себя в волшебном стекле есть нечто большее?
Всю свою историю человек пытается познать мир. Но познание мира это, в первую очередь, познание себя.
П ервый
вопрос, которым задается тот, кто пытается познать себя: «Кто я?»
Действительно, это основной вопрос. Ответ на него означает ответ на
многие другие вопросы, которые могли бы быть заданы. Итак, кто я,
человек? А что такое человек? Или - кто такой человек? Птица, рыба
или дикий зверь? Любое определение нуждается в четкой формулировке,
иначе оно слишком размыто и может предполагать несколько
толкований. А нас устроит только однозначность.
ервый
вопрос, которым задается тот, кто пытается познать себя: «Кто я?»
Действительно, это основной вопрос. Ответ на него означает ответ на
многие другие вопросы, которые могли бы быть заданы. Итак, кто я,
человек? А что такое человек? Или - кто такой человек? Птица, рыба
или дикий зверь? Любое определение нуждается в четкой формулировке,
иначе оно слишком размыто и может предполагать несколько
толкований. А нас устроит только однозначность.
Платон определил человека как бесперое двуногое. Очевидно, он никогда не видел кенгуру или циркового медведя. Эту формулировку блестяще опроверг Диоген. Он ощипал цыпленка и бросил его к ногам Платона со словами: «Вон он, твой человек!» Тогда Платон уточнил определение: человек - это существо бескрылое, двуногое, с плоскими ногтями; единственное из существ, восприимчивое к знанию, основанному на рассуждениях.
Казалось бы, эта формулировка действительно описывает человека. Но, с точки зрения стороннего наблюдателя, собаки в опытах Павлова тоже проявляли способность к рассуждению.
Гораздо проще указать на человека и сказать: «Вот это - человек!» То есть, дать определение на основании визуализации. Издавна слова «познать» и «увидеть» считаются синонимами. Мы говорим «я видел собственными глазами», считая это достаточным доказательством существования явления. Язык отразил эту синонимичность. Так, во французском языке «reflet» - отражение, «reflechir» - размышлять; в английском «speculate» - размышление, «speculum» - зеркало; в немецком «reflektieren» - отражать, рассчитывать, размышлять; в русском языке - созерцание, зерцало (зеркало).
Но как же увидеть себя? Частично - да, возможно. Но целиком… Не зря ведь говорят: не видать чего-то, как собственных ушей. Мы не можем увидеть собственную голову, не можем оказаться вне собственного тела, обойти себя кругом, рассмотреть спину. То есть, визуализация является неполной. И вот, пока человек мучается в сомнениях, пытаясь определить самого себя, в игру вступает зеркало. Посмотрев на свое отражение, сравнив его с окружающими, можно смело заявлять: «Я - человек!»
Следовательно, зеркало можно назвать техническим инструментом нашей самоидентификации, которая является основой в познании мира. Наши самосознание, представление о себе и мире, формируются с помощью и под влиянием зеркала.
Иногда мы принимаем зазеркалье, как отдельный мир, живущий по своим законам, населенный нашими двойниками и двойниками окружающих нас вещей. Так что же, собственно говоря, происходит в зазеркалье? По каким законам оно живет?
Зеркала - явление сложное и малоизученное, поэтому, с моей точки зрения, их нужно рассматривать со всех сторон, чтобы понять хотя бы часть свойств, проявляемых этими таинственными предметами. Так что от философии перейдем к математике.
Математика Зазеркалья
Совсем по другому поводу, из любопытства и из-за несмышленого котенка Кити, «Алиса оказалась на каминной полке, хоть и сама не заметила, как она туда попала… Зеркало стало таять, словно серебристый туман по утру. Через миг Алиса прошла сквозь зеркало и легко спрыгнула в Зазеркалье». Её там удивили ожившие портреты и, разговаривавшие между собой, шахматные фигуры.
Но она оставалась невидимой и неслышимой для обитателей высокомерного пространства. Возможно, размерность Зазеркального пространства, в котором оказалась Алиса, была дробной - 3,1415926535897932384664338327950288419716 9399375105820974944592 (здесь всего 63 знака после запятой, а Кэрролл придумал мнемоническое правило для запоминания последовательного ряда цифр, с помощью которого помнил «число π» до 71-го знака после запятой).
В зеркале все предметы «переворачиваются», предстают обращенными. Если вы протянете своему отражению правую руку, то увидите, что оно протягивает вам левую. Вот что пишет Л. Л. Кэрролл: «… я тебе расскажу все, что знаю про Зазеркальный дом. Во-первых, там есть вот эта комната, которая начинается прямо за стеклом. Она совсем такая же, как наша гостиная… только все там наоборот!»
К ак-то
я видела задачу, решение которой мне очень понравилось. Вот она -
зеркало переворачивает изображение. Это всем известно и очевидно,
стоит только посмотреть в зеркало. Но почему в своем зеркальном
отражении мы видим, что зеркало меняет левую и правую стороны, но
не меняет верх и низ, хотя по условиям симметрии меняться должны
все направления?
ак-то
я видела задачу, решение которой мне очень понравилось. Вот она -
зеркало переворачивает изображение. Это всем известно и очевидно,
стоит только посмотреть в зеркало. Но почему в своем зеркальном
отражении мы видим, что зеркало меняет левую и правую стороны, но
не меняет верх и низ, хотя по условиям симметрии меняться должны
все направления?
Оказывается, когда мы стоим перед зеркалом, то мысленно как бы обходим его сбоку и становимся за ним. Поэтому меняется правое с левым. А вот если представить, что мы перевалились через зеркало сверху, чтобы голова была внизу, то тогда казалось бы, что поменялся верх и низ, а левое и правое остались на месте. Нормальный человек, естественно, скорее «обойдет» зеркало, чем будет «переваливаться» через него.
Чтобы оказаться в нужном времени и нужном измерении, Алисе было достаточно спуститься по лестнице новым способом. «Она только положила руку на перила - и тихонько поплыла вниз по ступенькам, даже не задевая их ногами» (только через 60 лет будет изобретён эскалатор).
Параллельные миры Зазеркалья, сквозь которые проходит королевская пешка Алиса, размечены для неё Белой Королевой: «- Пешка, как ты знаешь, первым ходом прыгает через клетку. Так что на третью клетку ты проскочишь на всех парах - на паровозе, и тут же окажешься на четвёртой. Там ты повстречаешь Труляля и Траляля… Пятая клетка залита водой, а в шестой расположился Шалтай-Болтай… Седьмая клетка вся заросла лесом, но ты не беспокойся: один из Рыцарей на Коне проведёт тебя через лес, а на восьмой линии мы встретимся как равные - ты будешь Белой Королевой».
Сказка построена по принципу перевёрнутого, зеркального отражения. Зеркально, но асимметрично расположены вокруг королевской пары ладьи, кони и слоны. Точное зеркальное отражение представляют фигуры противника.
Физика Зазеркалья
Ещё до того как Алиса попала в Зазеркальный дом, у неё было в целом правильное представление о том, как он должен выглядеть:
«− Во-первых, там есть вот эта комната, которая начинается прямо за стеклом. Она совсем такая же, как наша гостиная, Китти, только всё там наоборот! Когда я залезаю на стул и смотрю в Зеркало, она видна мне вся, кроме камина. Ах, как бы мне хотелось его увидеть! Но в это Зеркало, как ни гляди, камина не увидишь… А книжки там очень похожи на наши - только слова написаны задом наперёд. Я это точно знаю, потому что однажды я показала им нашу книжку, а они показали мне свою!
…А дальше идёт коридор. Если распахнуть дверь в нашей гостиной пошире, можно увидеть кусочек коридора в том доме, он совсем такой же, как у нас».
В сё
ли так просто и правильно в этом описании, как кажется на первый
взгляд? Действительно ли в комнате за стеклом должно быть всё
наоборот? И что значит в данном случае наоборот? Почему, стоя по
эту сторону зеркала, камина не увидишь, как ни старайся? Всегда ли,
поднеся книгу к зеркалу, мы увидим слова, написанные задом наперёд?
Или книжку надо поднести каким-то определённым образом? Одним
словом, придётся поломать голову.
сё
ли так просто и правильно в этом описании, как кажется на первый
взгляд? Действительно ли в комнате за стеклом должно быть всё
наоборот? И что значит в данном случае наоборот? Почему, стоя по
эту сторону зеркала, камина не увидишь, как ни старайся? Всегда ли,
поднеся книгу к зеркалу, мы увидим слова, написанные задом наперёд?
Или книжку надо поднести каким-то определённым образом? Одним
словом, придётся поломать голову.
Плоское зеркало меняет местами правую и левую стороны всех предметов, поэтому предметы с вертикальной плоскостью (или осью) симметрии выглядят в нём так же, как и всегда, у остальных же половинки переставлены местами. Однако не все предметы в комнате отражаются в зеркале целиком, а некоторые вообще не видны.
Смотрящему в зеркало человеку предмет виден в том случае, когда световые лучи от него попадают в глаз, предварительно отразившись от поверхности зеркала. Если эти лучи до неё вообще не доходят, никакого отражения не возникает. Алиса права: глядя в зеркало, камина не увидишь, за исключением верхней части каминной полки, на которой оно укреплено.
Наконец, строки в книге будут выглядеть в зеркале написанными задом наперёд, если поднести книгу к плоскости зеркала или правым, или левым краем.
Законы движения в зазеркалье так же вывернуты, как и неподвижные отражения. В самом деле, если в ответ на помахивание правой рукой отражение машет левой, то если вы желаете попасть в какое-то место в зазеркалье, нужно идти прямо в противоположную сторону.
Маленькая Алиса Л. Кэрролла этого не знала, поэтому «… куда бы она ни шла, где бы ни сворачивала, всякий раз, хоть убей, она выходила снова к дому». И только пойдя в противоположном направлении, она вышла туда, куда хотела.
Алиса повстречалась с Чёрной Королевой? Для того чтобы приблизиться к ней, девочке пришлось идти... в противоположном направлении. Читаем в сказке:
«Вон она идет! − закричал молоденький Шпорник.
Алиса радостно оглянулась − и увидела Чёрную Королеву.
− Пойду-ка я к ней навстречу, − сказала Алиса.
− Навстречу? − переспросила Роза. − Так ты её никогда не встретишь! Я бы тебе посоветовала идти в обратную сторону!
− Какая чепуха! − подумала Алиса.
Впрочем, вслух она ничего не сказала и направилась прямо к Королеве. К своему удивлению, она тут же потеряла её из виду и снова оказалась у порога дома.
В сердцах она отступила назад, огляделась по сторонам в поисках Королевы, которую наконец увидала вдали, и подумала: не пойти ли на этот раз в противоположном направлении?
Всё вышло как нельзя лучше. Не прошло и минуты, как она столкнулась с Королевой у подножья холма, куда раньше никак не могла подойти».
Но выбор направления - это еще не все. Любопытнее всего, с моей точки зрения, другое. В нашем мире скорость есть частное от деления расстояния на время, то есть: v=S/t. В зазеркальном мире все наоборот. Там v=t/S.
«При большой скорости время велико, а расстояние мало. Чем выше скорость, тем меньше пройденное расстояние. Чем быстрее бежала Алиса во времени, тем более она оставалась на том же месте в пространстве» (Alexander L.Taylor.Though the Looking-Glass).
Л. Кэрролл был не просто сказочником, а математиком, рассказывающим сказку, и смог предвосхитить Энштейна. «Самое удивительное было то, что деревья не бежали, как следовало ожидать, им навстречу; как ни стремительно неслись Алиса и Королева, они не оставляли их позади… «Далеко еще?» - с трудом вымолвила, наконец, Алиса. «Не еще, а уже! - ответила Королева. - Мы пробежали мимо десять минут назад! Быстрее!» - сложно двигаться в зазеркальном мире тому, кто привык к законам «предзеркалья».
Это следствие закона движения, приведенного выше: при большой скорости время велико, а расстояние мало. Чем выше скорость, тем меньше пройденное расстояние. Чем быстрее бежала Алиса во времени, тем более она оставалась на том же месте в пространстве.
Оказывается, пироги в Зазеркалье сначала раздают гостям и только потом режут на части!
«− Что ж, угости нас пирогом, Чудище, − сказал Лев и улёгся на траву, положив подбородок на лапы.
…Алиса сидела на берегу ручейка, поставив большое блюдо себе на колени, и прилежно водила ножом.
− Ничего не понимаю! − сказала она Льву (она уже почти привыкла к тому, что её зовут Чудищем). − Я уже отрезала несколько кусков, а они опять срастаются!
− Ты не умеешь обращаться с Зазеркальными пирогами, − заметил Единорог. − Сначала раздай всем пирога, а потом разрежь его!
Конечно, это было бессмысленно, но Алиса послушно встала, обнесла всех пирогом, и он тут же разделился на три части.
− А теперь разрежь его, − сказал Лев, когда Алиса села на своё место с пустым блюдом в руках».
Д ля
жителей Зазеркалья совершенно естественно, что утолить жажду можно,
съев несколько сухариков; что за одно яйцо следует заплатить пять
пенсов, а за два - всего два. Чтобы перестала идти кровь из пальца,
его надо уколоть булавкой, а чтобы остаться на том же месте, нужно
бежать со всех ног. Вспомните, как Белая Королева рассказывает
Алисе о преимуществах жизни «в обратную сторону»! Например, в
Зазеркалье «завтра никогда не бывает сегодня», а лучше всего
обитателям Зазеркалья помнится то, что только случится через
некоторое время.
ля
жителей Зазеркалья совершенно естественно, что утолить жажду можно,
съев несколько сухариков; что за одно яйцо следует заплатить пять
пенсов, а за два - всего два. Чтобы перестала идти кровь из пальца,
его надо уколоть булавкой, а чтобы остаться на том же месте, нужно
бежать со всех ног. Вспомните, как Белая Королева рассказывает
Алисе о преимуществах жизни «в обратную сторону»! Например, в
Зазеркалье «завтра никогда не бывает сегодня», а лучше всего
обитателям Зазеркалья помнится то, что только случится через
некоторое время.
Целая глава в книге посвящена зеркальным близнецам Труляля и Траляля. Кстати, любимое выражение Траляля «Задом наперёд, совсем наоборот!» как нельзя лучше характеризует суть описанных Л.Л. Кэрролллом превращений: зеркало изменяет последовательность, в которой расположены точки на прямой (события во времени), на обратную.
Неудивительно, что пространство, имеющее такие законы, всегда представляется загадочным. А загадочное кажется опасным. Умберто Эко в «Маятнике Фуко» пишет: «Если имеется зеркало, это уже просто, по Лакану: вам хочется посмотреться в него. Но ничего не выходит. Вы меняете положение, ищете такого положения в пространстве, при котором зеркало вас отобразит, скажет: «вот ты, ты тут». И совершенно невозможно примириться с тем, что зеркала Лавуазье, выпуклые, вогнутые и еще бог весть какие, отказываются вести себя нормально, издеваются над вами: отступите на шаг - и вы в поле зрения, шагнете хоть чуть-чуть - и теряете себя. Этот катоптрический театрик создавался специально для разрушения вашей личности, то есть вашего самоощущения в пространстве… Появляется неуверенность не только в себе, но и во всем прочем. Исчезают вполне реальные вещи, которые вы видите рядом с собой… нормальное зеркало отражает получаемые из вогнутого лучи таким образом, что собственно предмета, очертаний его в зеркале не видно, ощущается нечто призрачное, мимолетное и к тому же перевернутое вверх ногами, где-то в воздухе, вне зеркала…»
Подобные «фокусы» зеркал привели к формированию множества мифов, сказок, легенд, мистических историй. Но все эти истории не имеют к математике даже условного отношения, поэтому мы рассмотрим небольшую часть того, что назовем «Легенды зеркал».
От математики - к легендам. Но это и не удивительно. Любое понимание какого-либо явления начинается с его описания. Легенды и есть такое описание.
Ребенок, впервые увидев себя в зеркале, удивляется. Он не сразу начинает воспринимать отражение, как свою копию. Скорее, он считает, что это - другой ребенок. И в сознании откладывается мысль, что там, за зеркальным стеклом, кто-то живет. И ребенок приходит к понятию «двойника».
Двойник - это тот, кто живет в зеркале, в зазеркальном мире. Он очень похож на оригинал, но, тем не менее - другой, обладающий самостоятельностью.
Подсознательно каждый человек чувствует себя связанным со своим двойником в зеркале: разбитое (умершее) зеркало несет несчастье и смерть своему хозяину. То есть, «смерть» зеркального двойника означает смерть оригинала.
У многих народов существовал свадебный обряд, когда жених и невеста должны были смотреться в одно зеркало, словно связь зеркальных двойников должна укрепить и благословить земной брак. Более того, у некоторых народов жених и невеста видели друг друга впервые именно отраженными в зеркале. То есть, знакомство происходило через зеркальных двойников. Считалось, что именно это должно принести счастье семье.
Мне кажется, что практически у каждого в жизни было такое: когда смотришь на свое отражение рядом с дорогим человеком и говоришь: «Посмотри, милый (-ая), как мы хорошо вместе смотримся!» И это «хорошо вместе смотримся» наполняло дополнительной уверенностью в собственных силах. А ведь это - отголосок веры в самостоятельное существование двойника, и его улыбающееся лицо доставляет радость, на какой-то момент становясь лицом постороннего счастливого человека. Независимо от возраста, мы продолжаем верить в самостоятельность зеркального отражения.
Мне вспоминается цитата: «… Скоро тебе становится так одиноко, что ты начинаешь заговаривать с ящерицами, а потом приходит время, когда они начинают тебе отвечать…» (Фредерик Браун, «Арена»). Как часто вы разговариваете с зеркалом? По утрам мы говорим зеркалу: «Привет! Что-то у тебя сегодня помятая физиономия», или «Ты сегодня неплохо выглядишь!» Вечером, глядя в зеркало, мы говорим: «Спать пора, и вид уже совершенно сонный, вон глаза сами закрываются». Казалось бы, мы разговариваем сами с собой. Но это вовсе не признак одиночества. Возможно это - беседа со своим двойником. Может быть, когда-нибудь он ответит.
Хорхе Луис Борхес упоминает о зеркальных существах, в частности, миф о Рыбе: «В те времена, в отличие от нынешнего времени, мир зеркал и мир людей не были разобщены. Кроме того, они сильно отличались, - не совпадали ни их обитатели, ни их цвета, ни их формы. Оба царства, зеркальное и человеческое, жили мирно, сквозь зеркала можно было входить и выходить. Однажды ночью зеркальный народ заполонил землю. Силы его были велики, однако после кровавых сражений победу одержали чары Желтого Императора. Он прогнал захватчиков, захватил их зеркала и приказал им повторять, как бы в некоем сне, все действия людей, лишил их силы и облика и низвел до последнего рабского положения. Но придет время, и они пробудятся от колдовской летаргии.
Первой проснется Рыба… Затем одна за другой пробудятся и остальные формы. Постепенно они станут отличными от нас, перестанут нам подражать. Они разобьют стеклянные и металлические преграды, и на этот раз их не удастся победить. Вместе с зеркальными тварями будут сражаться водяные». (Хорхе Луис Борхес «Энциклопедия вымышленных существ»)
Тот же Л. Кэрролл пишет: «Если распахнуть дверь в нашей гостиной пошире, можно увидеть кусочек коридора в том доме, он совсем такой же, как у нас. Но, кто знает, вдруг там, где его не видно, он совсем другой?» («Алиса в Зазеркалье»). Вот оно, вечное опасение - а вдруг зеркала только притворяются покорными и смирными? Вдруг то, что они показывают - это совсем не наше отражение?
Кстати сказать, именно на вере в то, что отражение в зеркале - двойник - это не совсем мы, основан один из методов психотерапии. Врач-скульптор создает скульптурный портрет пациента в натуральную величину, в реалистическом стиле. По мере того, как пациент узнает себя в этом скульптурном портрете, а портрет приближается к завершению, болезнь проходит. Портрет этот неуловимым образом носит на себе печать болезни, а оригинал исцеляется. Скульптурный портрет - это тот «двойник», которого больной каждый день видит в зеркале. Созданный врачом «двойник» становится «плохим» членом пары человек-отражение, а пациент - «хорошим».
Легенды говорят о том, что в старинных зеркалах заключены души всех, кто смотрелся в них. Считается, что если зеркало хранит отражение злого человека, покойника, убийцы, или «видело» сцену убийства, то оно само становится «злым». Такое зеркало всегда холодное на ощупь, перед ним гаснут церковные свечи, и оно может принести неприятности новому хозяину, вплоть до его смерти. Это зеркало нужно разбить, и только так можно избавиться от проклятия, которое в нем заключено.
Также говорят, что через зеркало можно «навести порчу». Если какой-либо человек посмотрит в ваше зеркало с пожеланиями зла, то эти пожелания могут исполниться. То есть, зеркало станет своеобразным накопителем и излучателем негативной энергии.
С помощью зеркал можно не только «наводить порчу», но и избавляться от нее. Например, если повесить зеркало в той комнате, где собираются гости, то оно заберет все злое себе. Потом зеркало следует очистить, пока оно является только накопителем, а не излучателем. Очистку рекомендуется производить холодной водой.
Еще считается, что если смотреть в зеркало, желая себе самого хорошего, заняться перед ним чем-то вроде аутотренинга, уверяя свое отражение, что оно - самое умное, самое красивое, самое-самое замечательное, то двойник, живущий в зеркале, обеспечит осуществление этих мечтаний.
Есть еще поверье, что, возвращаясь домой с полдороги, нужно обязательно посмотреться в зеркало. Это делается для того, чтобы восстановить защиту дома от посторонних воздействий, ту защиту, которую обеспечивает зеркало, отражая все негативные воздействия.
Существуют даже правила размещения зеркал в квартире. Например, любое зеркало следует вешать так, чтобы оно не «срезало» голову самого высокого члена семьи.
С помощью зеркал можно гадать. Самый известный метод - с помощью двух зеркал и свечи или с помощью одного зеркала и свечи. Святочные гадания на жениха известны с давних времен. И сейчас гадают таким образом, кто в шутку, а кто и всерьез. И даже то, что начинается как шутка, становится чем-то серьезным и настоящим, когда перед глазами в темноте разворачивается бесконечный зеркальный коридор.
Даже зарегистрированы случаи «проникновения» в прошлое и будущее с помощью зеркал. Кто-то уверяет, что видел в зеркале при гадании своего будущего мужа, кто-то - жену; записана история о том, как две девушки наблюдали в зеркале встречу императоров Александра I и Наполеона в 1807 году; рассказывают, как деревенские знахарки с помощью зеркала находят вора… В общем, эти истории почти бесконечны и столь же разнообразны, но все сводятся к одному: зеркала являются предметами, способными показать что-то неведомое, раскрыть новые знания, если с ними правильно обращаться.
Физика, с моей точки зрения, − это то, что помогает понять явления, объяснить легенды, найти рациональное обоснование запредельному.
Рассмотрим обычный процесс отражения упрощенно, на уровне школьного курса физики. Не будем углубляться в квантовую механику и прочие научные премудрости. Посмотрим, что можно увидеть, исходя из самых элементарных понятий.
Существует падающая волна, отражающая поверхность и отраженная волна. Как известно, падающая волна не идентична отраженной. Этим свойством отражающих поверхностей успешно пользуются. Например, оно применяется для исследования состава, свойств и структуры вещества. Ранее оптические характеристики вещества, необходимые для выяснения его свойств и структуры, определялись в основном по параметрам проходящего света. Между тем, свет, отраженный от вещества, несет в себе не меньшее, а зачастую большее количество информации о свойствах этого вещества. Эта информация не идентична получаемой «на просвет» и дополняет ее.
Но мы-то, стоя перед зеркалом, благополучно забываем все то, чему нас учили в школе. Мы доверчиво вглядываемся в гладкую поверхность, ожидая, что она сообщит нам истину. А все потому, что наше отражение похоже на то представление, которое мы составили о себе. Или мы уверили себя в том, что оно не просто похоже, а абсолютно соответствует истине. Но оно не является идентичным, не следует об этом забывать. Это - другая волна, с другими свойствами и характеристиками. Говоря проще: что-то осталось внутри зеркала, а что-то пришло к нам из зазеркалья. Фактически, если рассматривать процесс отражения, согласно понятий классической физики, можно сделать вывод, что действительно зеркало «хранит» в себе изображения всех, кто когда-либо смотрелся в него. Так что это не совсем бабушкина сказка.
Следует учесть и тот момент, что падающая волна состоит не только из видимого диапазона. Человек излучает еще и в невидимом диапазоне, соответственно, отраженная волна - это тоже не только видимый свет. Так что, если изменения между падающей и отраженной волной происходят в невидимом диапазоне излучения, то человек, смотрящийся в зеркало, их попросту не замечает.
Другое дело, на какой срок зеркало сохраняет полученную информацию. Посмотрим, что происходит с падающим светом внутри зеркала. Ведь не забивается же световая волна в угол, таясь там до того момента, когда зеркало разобьют.
П ри
отражении света от прозрачной среды суммарная энергия
электромагнитного поля остается неизменной, меняется лишь его
конфигурация (направление распространения). Однако уже в этом
случае происходят промежуточные процессы преобразования энергии.
Энергия падающей волны превращается (частично) в энергию
вынужденных колебаний частиц среды. Эти колебания порождают
вторичные волны. Сложение падающей волны с вторичными волнами
создает отраженные и преломленные волны. Все эти процессы
происходят в очень тонком слое вблизи границы раздела.
ри
отражении света от прозрачной среды суммарная энергия
электромагнитного поля остается неизменной, меняется лишь его
конфигурация (направление распространения). Однако уже в этом
случае происходят промежуточные процессы преобразования энергии.
Энергия падающей волны превращается (частично) в энергию
вынужденных колебаний частиц среды. Эти колебания порождают
вторичные волны. Сложение падающей волны с вторичными волнами
создает отраженные и преломленные волны. Все эти процессы
происходят в очень тонком слое вблизи границы раздела.
Но зеркало не является прозрачной средой. В зеркалах отражающей поверхностью является металл. В металлах падающая волна поглощается практически полностью в тонком слое (порядка 100 ангстрем), энергия ее превращается в основном в энергию движения электронной плазмы. Движущиеся электроны излучают, в результате чего формируется отраженная волна, уносящая до 99% и более первоначально поглощенной энергии; лишь малая доля уходит на «разогрев» решетки металла.
Таким образом, в отражающей среде имеется определенный запас энергии. Эта энергия доставляется в процессе установления и формирования отраженного поля, а в стационарном состоянии лишь поддерживается определенным потоком энергии из падающей волны. Запас этот в поглощающей среде (в зеркале) может быть значительным, даже при полном внутреннем отражении. В неоднородных, например, мутных и дисперсных, средах, время установления поля может быть значительным из-за большой глубины пробега фотонов, формирующих отраженный свет за счет многократного рассеяния. В этом случае может происходить процесс «пленения излучения». Чем больше неоднородность зеркала, тем больше энергии «пленяется».
Казалось бы, ну, застряло что-то в зеркале, ну и пусть. Все равно какие-то мелочи, которые сами по себе рассеются. А вот это не совсем верно. Самая простейшая аналогия - пластмасса и огонь. Представьте, что вы пронесли над огнем пластиковую линейку. Что будет? Правильно, нагреется. Но если пронести быстро, то никаких внешних изменений заметно не будет. А внутренние изменения произойдут. Но если тепловое воздействие совсем непродолжительное, то эти изменения будут несущественными. Теперь будем нести эту линейку медленнее. На этот раз уже начнутся и внешние изменения, пластик «потечет». Если же оставить линейку на огне, то в очень скором времени от нее останется только маленькая кучка спекшейся пластмассы.
То же и с зеркалом. Энергия, «пленяющаяся» внутри отражающего слоя, вызывает изменения этого слоя. Формируются носители информации по принципу выпуклость/вогнутость. Как дорожки на грампластинке. А неоднородность отражающей среды помогает удерживать все большее количество энергии, вызывающей формирование «матрицы образа». Получается, что чем больше человек смотрится в зеркало, тем отчетливее «отпечатывается» его образ внутри зеркала. То есть, ваше зеркало сохраняет в себе ваш образ. Если же кто-то посмотрел в ваше зеркало один раз, то его образ, конечно же, тоже сохранился, «наложившись» на вашу «матрицу». Но если постороннее воздействие непродолжительно, то его последствия очень быстро исчезнут49.
В сказках об Алисе множество загадок и ни одной отгадки, ни одного прямого ответа. Только умело поставленные вопросы и грамотно разбросанные по тексту подсказки, да едва уловимые намёки. Но это тот случай, когда не договорить, а лишь приоткрыть завесу тайны лучше, чем выдать все секреты и поделиться с читателями готовым знанием. Так стоит ли удивляться тому, что творения Льюиса Л. Кэрроллла, будучи превосходной пищей для размышлений, и по сей день будоражат пытливые умы? Как и тому, что кто-то вовсе не воспринимает тонкую интеллектуальную игру писателя? «Алиса…» открывает свои тайны тому, кто умеет смотреть и видеть, тому, кто сохранил в себе способность удивляться и воспринимать новое.
Заключение
Если идти в глубь нелепого, можно дойти до смысла, и наоборот: если идти честно в глубь смысла, обязательно дойдешь до бессмыслицы, хаоса. Эти вещи зеркальны. Что бы ни имел в виду Л. Кэрролл, когда писал эти книги, образы его получили независимое существование. Об «Алисе» написано огромное количество работ. Аллегории Л.Кэрролла получали в них самое различное толкование: политическое, психологическое, психоаналитическое, богословское, логическое, математическое, физическое, филологическое. Вероятно, на это есть свои основания. Даже если Л.Кэрролл не думал обо всех этих сложных материях, когда писал свою книгу, в ней ее могла не отразиться сложная внутренняя жизнь ученого и поэта.
Читая Л.Кэрролла, вглядываясь в знакомые с детства черты героев, мы видим пространство совершенно разных теоретических действительностей. Причем эти действительности необычны в силу того, что в основе каждой из них лежит какая-нибудь «необычная» идеализация: например, идеализация цикличного времени, или неоднородного пространства, или движения, не подвластного закону инерции и т.д. В конечном счете кэрролловская «страна чудес» оказывается таким миром, где то и дело не «срабатывают» привычные знания, где постоянно трансформируются базисные идеализации. Как говорил Эйнштейн, чудо − это когда «восприятие вступает в острый конфликт с достаточно установившимся в нас миром понятий».
Читая сказки об Алисе, можно предположить, что Кэрролл занимался обыгрыванием разных нарождавшихся теорий знания и пытался ввести детей в мир живой науки, живого знания на доступном им уровне.
В качестве таких нарождавшихся теорий комментаторы выделяют:
− теорию Эдмунда Уитеккера про уменьшающуюся вселенную;
− дискуссии о том, можно ли упасть сквозь Землю и как это падение могло бы происходить (Бэкон, Галилей);
− обсуждение разных теорий времени, проблематизирующих теорию линейного времени, в частности модель космоса, предложенную Де Ситтером, в которой течение времени остановилось;
− модель зеркального воспроизведения линейного времени;
− теорию епископа Беркли о том, что все материальные предметы, включая нас самих, просто снятся Господу (эпизод − рассуждения Алисы с Труляля и Траляля о сне Черного Короля, а также конечный эпизод в «Алисе в стране чудес»);
− теорию семиотического устройства мира (между предметами и их названиями нет никакой связи;
− теорию стереоизомерии, открытие которой было якобы предвосхищено самим Л.Кэрроллом и т.д.
Желая лишить изучающего логику ориентиров, подсказываемых здравым смыслом, Л.Кэрролл придумал логические задачи, в которых посылки находились в вопиющем противоречии с повседневным опытом. Но правила вывода, подобно улыбке Чеширского Кота, оставались и после того, как угасала надежда на помощь здравого смысла. Именно эти правила и позволяли найти решение задачи.
Отказываясь от логики здравого смысла, Л.Кэрролл приносит ее в жертву логике несравненно более глубокой, во многом напоминающей диалектическую логику современного научного исследования, подчас столь причудливую, что она кажется непостижимой, противоречивой и способной повергнуть в отчаяние не только человека, далекого от науки, но и самого исследователя.
Сказки про Алису удивительно многомерны. И если Алиса находится в рамках карточных или шахматных игр, то Льюис Кэрролл явно предлагает своим взрослым читателям игру ума, которая если имеет рамки, то только рамки приличия. Это, пожалуй, самая элитная и элегантная игра из известных в мире. Ставки и результат в ней бывают самые неожиданные. Достойных игроков, класса Кэрролла, в мире достаточно ограниченное количество, Но азарт и целеустремленность могут даже из пешки сделать Королеву.
Еще один аспект рассмотрения жанра литературной сказки Кэрролла предложила английский логик Элизабет Сьюэлл. Она рассматривает нонсенс Кэрролла как некую логическую систему, организованную по принципам игры, как некую интеллектуальную деятельность, требующую для своего построения, по меньшей мере, одного игрока, а также - некоего количества предметов, с которыми он мог бы играть. Такой "серии предметов" в нонсенсе становятся слова, представляющие собой по большей части названия предметов и чисел. "Игра в нонсенс" состоит в отборе и организации материала в собрание неких дискретных "фишек", из которых создается ряд отвлеченных, детализированных систем. В "игре в нонсенс", по мысли Сьюэлл, человеческий разум осуществляет две одинаково присущие ему тенденции - тенденцию к разупорядочиванию и тенденцию к упорядочиванию действительности. В противоборстве двух взаимно исключающих друг друга тенденций и складывается "игра в нонсенс". «Кэрролл вовсе не автор нонсенсов, − замечает Хэролд Блум. − Загадка − это не нонсенс».
Л. Кэрролл оказался непостижимым и самым замечательным выдумщиком, какой только был на свете, − кроме того, он сумел соединить мир абсурдной, нелепой фантазии с тонкой математической логикой. Он буквально сломал существовавшие до него традиционно скучные, обыденно серые и утомительные представления.
Таким образом, естественно-математический уровень является еще одним важным уровнем сказок Л.Кэрролла. Конечно, было бы упрощением представлять его в виде единого пласта, он рассеян по всему тексту, залегает на разной глубине. Вот почему логики, математики, физики, философы, психологи находят в "Алисе" материал для научных размышлений и интерпретаций. Не потому ли "Алиса" оказывается "самой неисчерпаемой сказкой в мире"?
Литература
-
Асмус В.Ф., Логика. −М.: Наука, 1947.
-
Библер В.С. К философской логике парадокса / В.С. Библер // Вопросы философии. - 1988. - №1. - С.28-42.
-
Большая советская энциклопедия. − М.: Советская энциклопедия. 1969-1978.
-
Борисенко А., Демурова Н., Льюис Кэрролл: мифы и метаморфозы.// Иностранная литература. - 2003, № 7.
-
Важдаев В. Л., Кэролл и его сказка.// Иностранная литература, 1995, № 7.
-
Варган С., Есть ли в зеркалах магия?, [Электронный ресурс] Опубликовано 12.09.2008 в рубрике «Фэн-шуй и непознанное», shkolazhizni.ru
-
Винокур В.Г. Парадоксы древней науки [Электронный ресурс] / В.Г. Винокур. - http: // www.stq.ru
-
Войшвилло Е.К. Логика: учеб. для студ. высш. учеб. заведений / Е.К. Войшвилло, М.Г. Дегтярев. - М.: Изд-во ВЛАДОСС-ПРЕСС, 2001. - 528 с.
-
Галинская И.Л., Л.Кэрролл и загадки его текстов −М.: ИНИОН РАН, 1995. 76 с.
-
Гетманова А.Д., Логика: Учебник для студентов пед. вузов. М.: Высш. шк., 1986. 288 с.
-
Гусев Д.А. Логика: Учебное пособие для вузов. −М.: ЮНИТИ-ДАНА, 2004.
-
Гарднер М., Аннотированная Алиса. - В кн.: Кэрролл Л. Приключения Алисы в Стране Чудес. Сквозь зеркало и что там увидела Алиса, или Алиса в Зазеркалье. 3-е изд., доп. - М., Наука, 1998. - 332с.
-
Данилов К.А., Смородинский Я.А., Физик читает Кэрролла, -М.: Время, 2000. 132с.
-
Делез Ж., Логика смысла. Пер. с фр. - М.: Раритет, 1998. 198с.
-
Демурова Н.М., Алиса в Стране Чудес и Зазеркалье. - В кн.: Кэрролл Л. Приключения Алисы в Стране Чудес. Сквозь зеркало и что там увидела Алиса, или Алиса в Зазеркалье. 3-е изд., доп. - М., Наука, 1998. 332с.
-
Демурова Н.М., Л.Кэрролл. Очерк жизни и творчества. -М.: Наука, 1999. 89с.
-
Дубровина В.П., Зеркальная метафора (на материале Л. Кэрролла «Алиса в Зазеркалье»).// Вестник АмГУ. - 2000, № 10.
-
Дьюи Д., Психология и педагогика мышления. Пер.с англ. Н.М.Никольской. М.: Совершенство, 1997. 208 с.
-
Ивин А.А. Логика: учебник / А.А. Ивин. - М.: Гардарики, 1999. 352 с.
-
Кузичев А.С. Диаграммы Венна. История и применения. М., 1968.
-
Кэрролл Л., История с узелками. - М.: Мир. 1973г. 408с.
-
Кэрролл Л., Охота на Снарка. Пер. с англ. Г.Кружкова, илл. Л.Тишкова - М.: Рукитис, 1991. 88 с.,
-
Кэрролл Льюис, Серия Шедевры классической поэзии для юных читателей. Худ. Сост. Е. Витковский, - М.: ЭКСМО, 2003г. 48с.
-
Кэрролл Л., Алиса в стране чудес. Алиса в Зазеркалье. -М.: ЭКСМО, 2004. 216с.
-
Кэрролл Л., Alice in wonderland / Алиса в стране чудес. Алиса в Зазеркалье: На английском языке. -М.: Глосса, 2001. 156с.
-
Новоселов М.М. Абстракция множества и парадокс Рассела / М.М. Новоселов // Вопросы философии. - 2003. - №7. - С. 67-77.
-
Падни Дж., Льюис Кэрролл и его мир. - М.: Радуга, 1992. 202с.
-
Платонов К.К. Краткий словарь системы психологических понятий. 2-еизд. М.: Высш. Школа, 1984.
-
Румянцев Д. Льюис Кэрролл и троичная машина // «Академия Тринитаризма», М., Эл № 77-6567, [Электронный ресурс] http: // info@trinitas.ru
-
Рубинштейн С.Л. О мышлении и путях его исследования. М.: АН СССР, 1958.
-
Смаллиан Р., Как же называется эта книга? - М.: Мир, 2001. 82с.
-
Сопоставительный анализ русских переводов Л. Кэрролла Alice in wonderland // Семантика и прагматика языка в диалоге культур. 1998, № 2.
-
Сухотин А.В. Парадоксы науки [Электронный ресурс] http: // bookz.ru
-
Тульчинский Г.Л., Льюис Кэрролл: нонсенс как предпосылка истины, [Электронный ресурс] hpsy.ru
-
Тульчинский Г.Л., О логическом учении Льюиса Кэррола // Философские науки. 1979, № 3, с.97-103.
-
Ушаков Д.Н., Толковый словарь Ушакова. [Электронный ресурс] 1935-1940. dic.academic.ru
-
Френкель А. и Бар-Хиллел И., Основания теории множеств, − М., 1966.
-
Фридман Л.М. Учитесь учиться математике: Кн. Для учащихся. М.: Просвещение, 1985. 112 с.
-
Юнг Карл Густав и др., Человек и его символы/ под общей ред. С.Н. Сиренко. - М.: Серебряные нити, 1998. 284с.
-
Эко У., Отсутствующая структура. - СПб.: Петрополис, 1998. 117с.
1 Толковый словарь Ушакова. Д.Н. Ушаков. 1935-1940. dic.academic.ru
2 Платонов К.К. Краткий словарь системы психологических понятий. 2-еизд. М.: Высш. Школа, 1984.
3 Дьюи Д. Психология и педагогика мышления. Пер.с англ. Н.М.Никольской. М.: Совершенство, 1997. 208 с.
4 Рубинштейн С.Л. О мышлении и путях его исследования. М.: АН СССР, 1958.
5 Гетманова А.Д. Логика: Учебник для студентов пед. вузов. М.: Высш. шк., 1986.-288 с.
6 Асмус В.Ф. Логика. М.: Наука, 1947.
7 Фридман Л.М. Учитесь учиться математике: Кн. Для учащихся. М.: Просвещение, 1985. 112 с.
8 Ивлев Ю. Логика для юристов. - М.: БЕК, 2001. - С. 22
9 Иванов Е.И. Логика. - М.: БЕК, 2001. - С. 19
10 Асмус В. Логика. - 1999. - С. 28
11 Гусев Д.А. Логика: Учебное пособие для вузов. - М.: ЮНИТИ-ДАНА, 2004.
12 Войшвилло Е.К., Дегтяренко М.Г. Логика. - М.: Владос - Пресс, 2001. - С. 35.
13 Иванов Е.И. Логика. - М.: БЕК, 2001. - С. 21
14 Кэррол Л., «Символическая логика», jwy.narod.ru/logic
15 Тульчинский Г.Л., Льюис Кэрролл: нонсенс как предпосылка истины, hpsy.ru
16 Тульчинский Г.Л. О логическом учении Льюиса Кэррола // Философские науки. 1979, № 3, с.97-103.
17 Кэрролл Льюис, Логическая игра. −М., 1991.
18 Колесников Н.Г. О логических исследованиях Льюиса Кэррола // Вестник МГУ. Сер.7. Философия. 1983, № 3, с.57-63; Колесников Н.Г. Формализация силлогистики Льюиса Кэррола // Логические исследования. М., 1983, с.45-58.
19 Кэррол Льюис, История с узелками, −М., 1973, с.341.
20 Маккалок У. Символическое изображение нейрона в виде некоторой логической функции // Принципы самоорганизации. М.. 1966, с.131-135.
21 Коуэн Дж. Многозначные логики и надежные автоматы //Самоорганизующиеся системы. М., 1964, с.178-225.
22 Кузичев А.С. Диаграммы Венна. История и применения. М., 1968.
23 Бизам Д., Герцог Я. Игра и логика. М., 1975.
24 Анализ аристотелевой теории предикации см. Попов П.С., Стяжкин Н.И. Развитие логических идей от Античности до эпохи Возрождения. М., 1974, с.50 и далее.
25 Попов П.С. История логики Нового времени. М., 1960, с.237.
26 Кэррол Льюис, История с узелками, −М., 1973, с.340.
27 Кэррол Льюис, История с узелками, −М., 1973, с.340.
28 Тульчинский Г.Л., Льюис Кэррол: нонсенс как предпосылка истины, hpsy.ru
29 Сухотин А.В. Парадоксы науки [Электронный ресурс] http: // bookz.ru
30 Библер В.С. К философской логике парадокса [Текст] / В.С. Библер // Вопросы философии. - 1988. - №1. - С.28-42.
31 Френкель А. и Бар-Хиллел И., Основания теории множеств, пер. с англ., М., 1966.
32 Сухотин А.В. Парадоксы науки [Электронный ресурс] http: // bookz.ru
33 Ивин А.А. Логика [Текст]: учебник / А.А. Ивин. - М.: Гардарики, 1999. 352 с.
34 Войшвилло Е.К. Логика [Текст] : учеб. для студ. высш. учеб. заведений / Е.К. Войшвилло, М.Г. Дегтярев. - М.: Изд-во ВЛАДОСС-ПРЕСС, 2001. - 528 с.
35 Большая советская энциклопедия. − М.: Советская энциклопедия. 1969-1978.
36 Ивин А.А. Логика [Текст]: учебник / А.А. Ивин. - М.: Гардарики, 1999. 352 с.
37 Новоселов М.М. Абстракция множества и парадокс Рассела [Текст] / М.М. Новоселов // Вопросы философии. - 2003. - №7. - С. 67-77.
38 Винокур В.Г. Парадоксы древней науки [Электронный ресурс] / В.Г. Винокур. - http: // www.stq.ru
39 Сухотин А.В. Парадоксы науки [Электронный ресурс] / А.В. Сухотин. - http: // bookz.ru
40 Сухотин А.В. Парадоксы науки [Электронный ресурс] / А.В. Сухотин. - http: // bookz.ru
41 Румянцев Д. Льюис Кэрролл и троичная машина // «Академия Тринитаризма», М., Эл № 77-6567, [Электронный ресурс] http: // info@trinitas.ru
42 Dialogo dei Massimi Sistemi, Giornata Seconda. Флорентийское издание, 1842 г., т. I, с. 251-252[11 - Русский перевод: Галилео Галилей. Диалог о двух главнейших системах мира, птолемеевой и коперниковой. М.-Л., Гослитиздат, 1948.
43 Кэрролл Л. Приключения Алисы в Стране Чудес. М., 1992. С. 58, 59.
44 Флоренский Павел. Абсолютность пространственности. // Собрание сочинений. - М., 2000.- С. 277.
45 С этой точки зрения очень интересна лекция Мирча Элиаде «Мир, город, дом». Элиаде пишет: «Мы знаем, что человек никогда не жил в таком пространстве, которое математики и физики называют изотропным, то есть имеющим одни и те же свойства по всем направлениям. Пространство, в человеческом восприятии, является ориентированным и, следовательно, анизотропным, ибо каждое измерение и направление имеет специфический смысл; например, вдоль вертикальной оси слово «верх» не просто противоположно «вниз», а имеет иной смысл; аналогично, вдоль горизонтальной оси, могут различаться по смыслу правое и левое. Вопрос состоит в том, имеет ли ощущение ориентированности пространства и другие подобные ощущения, связанные с намеренно структурированными пространствами (например, различными пространствами искусства и архитектуры), что-либо общее с чувством сакрального пространства для религиозного человека (Homo religiosus).» (Элиаде Мирча. Оккультизм, колдовство и моды в культуре.- К., 2002.- С. 55, 56).
46 Кэрролл Л. Приключения Алисы в Стране Чудес.- М., 1992.- С. 82.
47 «Перемещением частицы называют вектор S, проведенный из начального положения частицы в выбранной системе отсчета в ее конечное положение в той же системе отсчета.» (Энциклопедия для детей. -М., 2000.- Т. 16.- Физика. Ч. 1.- С. 319.)
48 Зелинский А.Н. Конструктивные принципы древнерусского календаря.- М., 1996.- С. 62.
49 Варган С., Есть ли в зеркалах магия?, Опубликовано 12.09.2008 в рубрике «Фэн-шуй и непознанное</</font>», shkolazhizni.ru
51