Конспект по математике 11 класс Смешанные тригонометрические уравнения

</

Тип урока: Урок обобщения и систематизации.

Методы:

- частично-поисковый;

- поисковый;

- проблемный;

-исследовательский - решение познавательных обобщающих задач;

- системные обобщения;

- самопроверка;

- самооценка.

Цель урока: Обобщить и систематизировать знания по теме «Тригонометрические уравнения», решение смешанных тригонометрических уравнений, продолжить работу по подготовке к ЕГЭ.

План урока:

● Устная работа (разминка)

● Самостоятельная работа (повторение)

● Проверка вариантов ЕГЭ (домашняя работа)

● Демонстрация решённых самостоятельно смешанных тригонометрических уравнений

● Самостоятельное решение смешанных уравнений.

● Индивидуально - консультационная работа.

● Итог урока.

Формы организацииурока:

- индивидуальная;

- фронтальная;

- групповая;

Оформление:

Крылатые выражения (девиз урока)

Орг. момент.

Сегодня на уроке мы продолжим работу над обобщением и систематизацией полученные знания по теме «Тригонометрические уравнения». На этом занятии мы будем решать смешанные тригонометрические уравнения, и тем самым - продолжаем подготовку к ЕГЭ. Работаем по следующему плану:

Устная работа. Диктант «Верно - неверно»

● Самостоятельная работа (повторение)

Для каждого варианта - задания на слайде, продолжите каждую запись. Время выполнения 3 минуты.

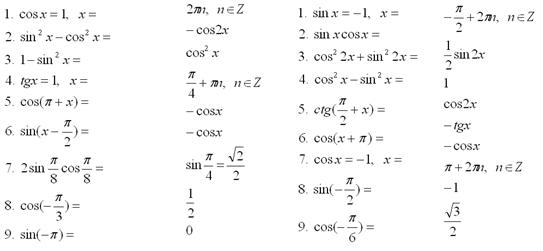
Критерий оценки: «5» - все 9 «+», «4» - 8 «+», «3» - 6-7 «+»

● Проверка вариантов ЕГЭ (домашняя работа).

● Демонстрация решённых самостоятельно смешанных тригонометрических уравнений. Отсканированные работы на слайдах. Ход решения кратко рассказывают ученики.

№ 511105. а) Решите уравнение

б) Найдите все корни этого уравнения, принадлежащие отрезку

Решение.

а) Преобразуем уравнение:

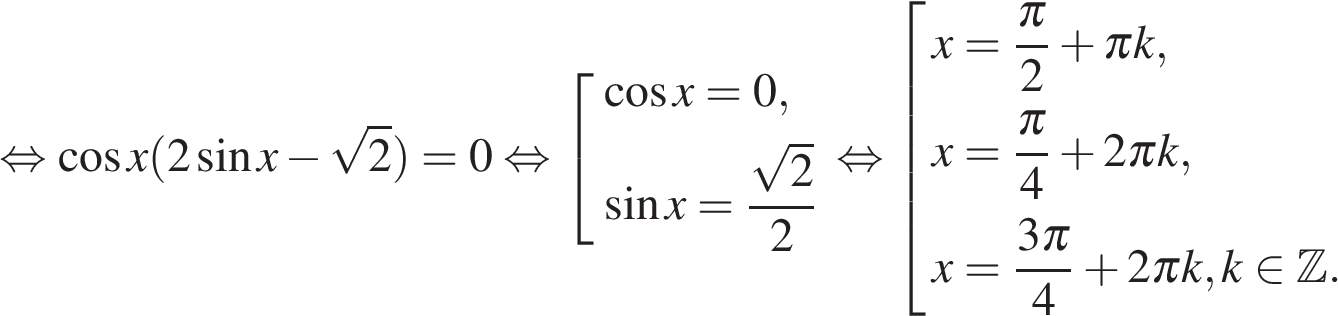
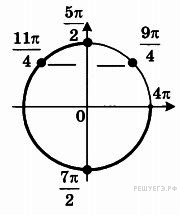
б) С помощью единичной окружности отберём корни на отрезке

Получаем:

Ответ: а) б)

№ 501689. а) Решите уравнение

б) Найдите все корни этого уравнения, принадлежащие отрезку

Решение.

а) Преобразуем исходное уравнение:

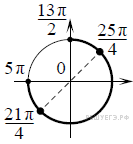
б) С помощью числовой окружности отберем корни, принадлежащие отрезку Получим числа:

Ответ: а) б)

№ 502313. а) Решите уравнение

б) Найдите все корни этого уравнения, принадлежащие отрезку

Решение.

а) Запишем исходное уравнение в виде:

Значит, либо откуда либо откуда или

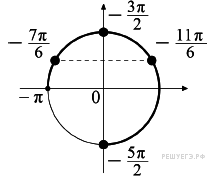
б) С помощью числовой окружности отберём корни, принадлежащие отрезку Получим числа:

Ответ: а) б)

№ 505565. а) Решите уравнение

б) Укажите корни этого уравнения, принадлежащие отрезку

Решение.

Заметим, что: Далее имеем:

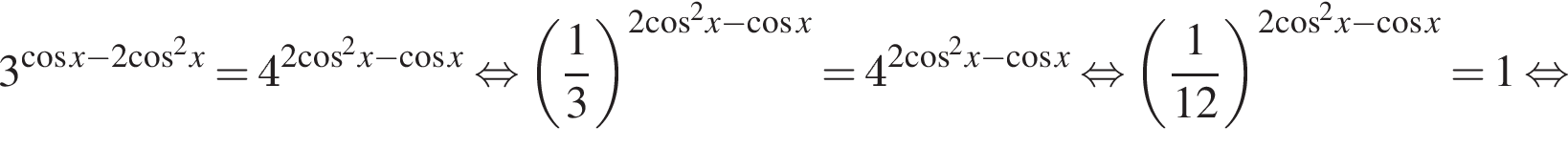
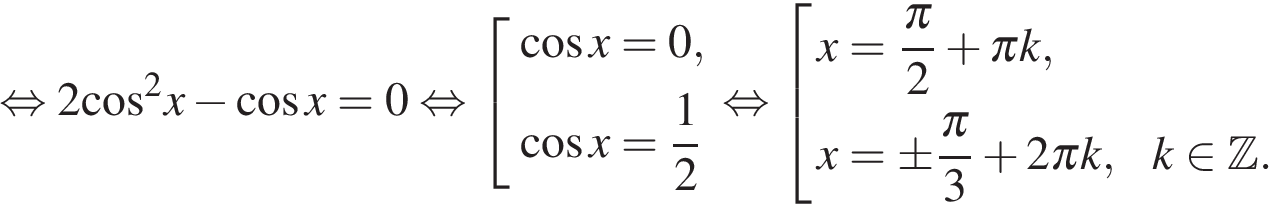
Заданному промежутку принадлежат числа

Ответ: а) б)

а) Решите уравнение

б) Найдите все корни этого уравнения, принадлежащие отрезку

Решение.

а) Последовательно получаем:

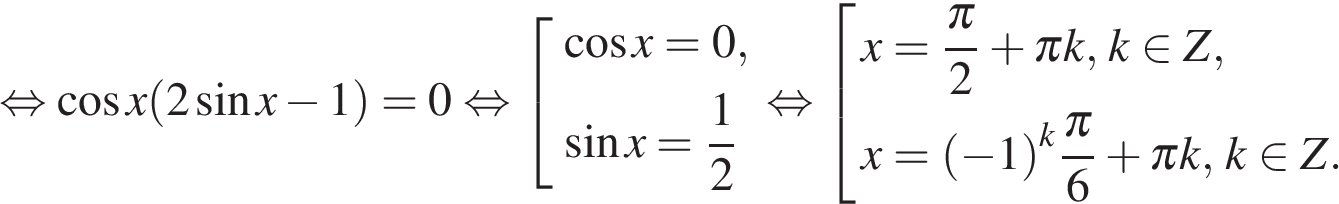
б) Условию удовлетворяет только числа

Ответ: а) ; б)

● Самостоятельное решение смешанных уравнений.

log₅ (cos x − sin 2x + 25) = 2

Перепишем Все уравнение с учетом этого факта:

log₅ (cos x − sin 2x + 25) = log₅ 25

Перед нами каноническое логарифмическое уравнение. В нем мы можем смело убрать знаки логарифма (т.е. просто приравнять аргументы логарифмов). Получим:

cos x − sin 2x + 25 = 25

Перед нами тригонометрическое уравнение. Переносим 25 влево и получаем:

cos x − sin 2x = 0

Формула синуса двойного угла

В данном случае все очень легко. Вспоминаем формулу синуса двойного угла:

sin 2x = 2sin x · cos x

Подставляем это выражение в наше уравнение:

cos x − 2sin x · cos x = 0

Мы видим, что и в первом, и во втором слагаемом есть cos x. Выносим его за скобку:

cos x (1- 2sin x ) = 0

Произведение равно нулю, когда хотя бы один из множителей равен нулю:

либо cos x = 0, либо 1 − 2sin x = 0

Перед нами совокупность из двух простейших тригонометрических уравнений:

cos x = 0; 1 - 2sin x = 0.

-2sin x = -1;

sin x = 1/2.

cos x = 0; sin x = 1/2.

Вспоминаем, что cos x = 0 - это частный случай, поэтому x = π/2 + πn, n ∈ Z.

sin x = 1/2;x = π/6 + 2πn, n ∈ Z, x = 5π/6 + 2πn, n ∈ Z.

Ответ: x = π/2 + πn, x = π/6 + 2πn, x = 5π/6 + 2πn, n ∈ Z.

2). ( 2sinx - )∙ log₃ (tgx) = 0.

Решение: ( 2sinx - )∙ log₃ (tgx) = 0, ОДЗ: tgx > 0

2sinx - = 0 или log₃ (tgx) = 0

sinx = tgx = 1

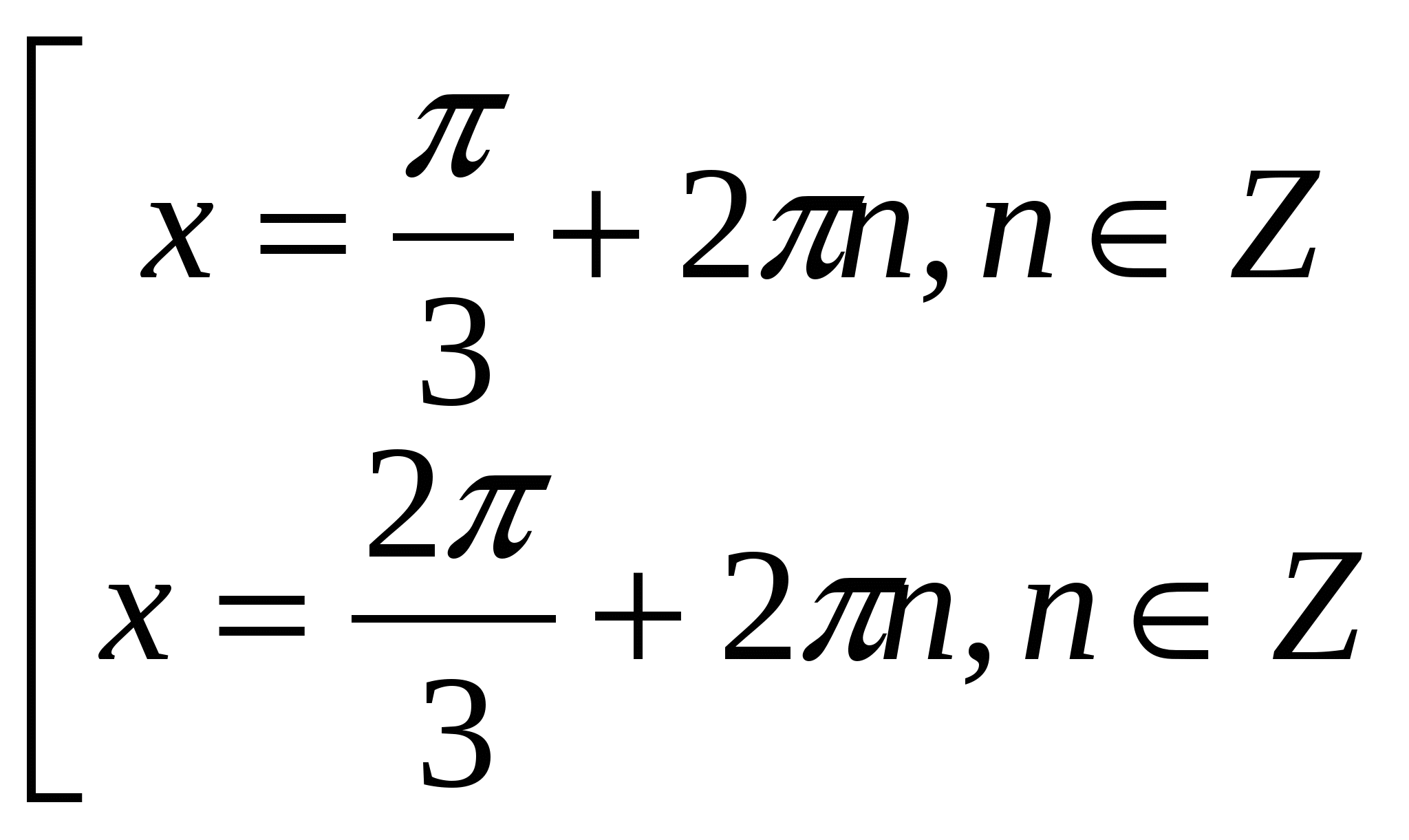х =

Заметим, что x=не удовлетворяет ОДЗ

Ответ: ; .

● Индивидуально - консультационная работа. Ученики могут начинать решение с любого уравнения при необходимости за советом или помощью обращаются к одноклассникам или ко мне.

№ 484551. Решите уравнение

Решение.

Уравнение равносильно системе

Из неравенства получаем, что . В уравнении сделаем замену и решим уравнение или Равенствам и на тригонометрической окружности соответствует четыре точки. Две из них, находящиеся в верхней полуплоскости, не удовлетворяют условию

Получаем решения:

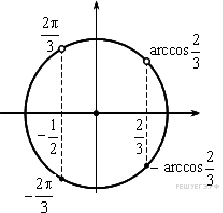
Ответ:

№ 484552. Решите уравнение

Решение.

Уравнение равносильно системе

Решим уравнение:

Тогда или . Последнее уравнение не имеет решений, а из первого, учитывая, что , получаем: .

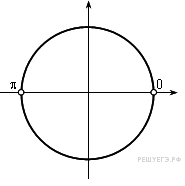
Ответ: .

№ 507620. Решите уравнение:

Решение.

Уравнение равносильно системе:

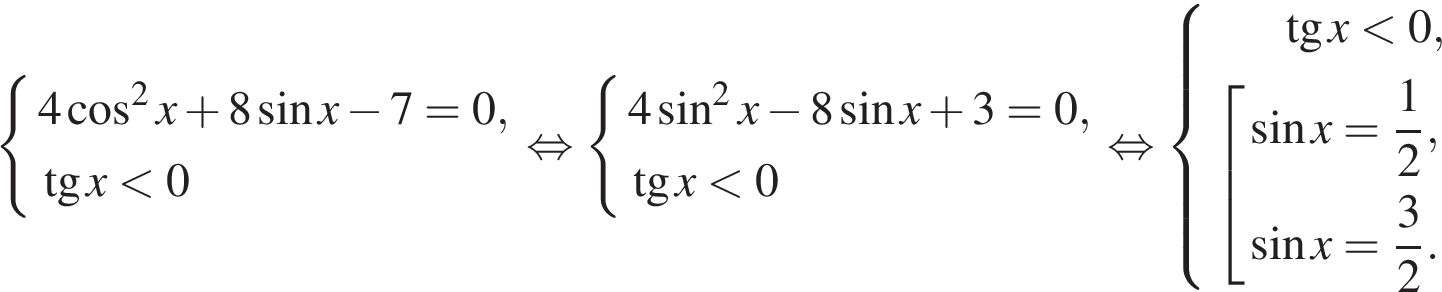
Уравнение решений не имеет. Учитывая, что получаем:

Ответ:

№ 507633. Решите уравнение

Решение.

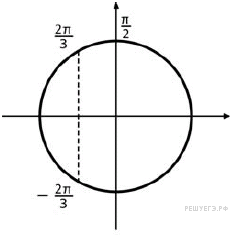Левая часть уравнения имеет смысл при Приравняем числитель к нулю:

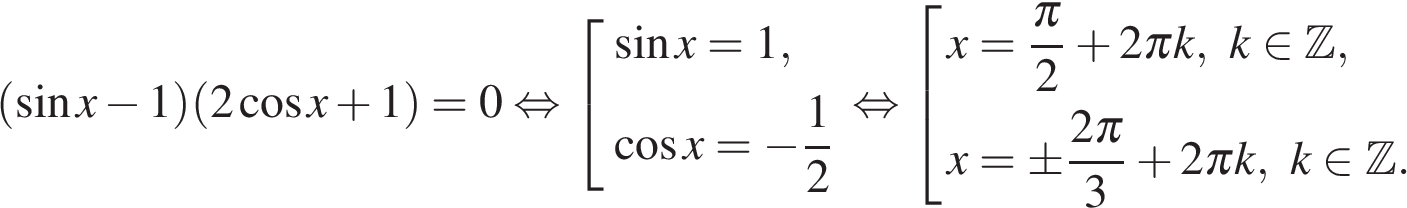
Учитывая условие получаем, что числа не являются решениями данного уравнения. Учитывая условие получаем, что числа не являются решениями данного уравнения.

Ответ:

№ 507656. Решите уравнение

Решение.

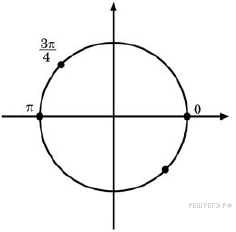Перейдём к системе:

Решим первое уравнение:

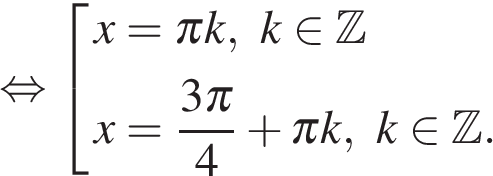
Учитывая, что получаем:

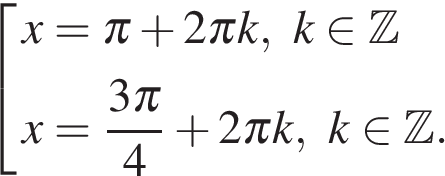
Ответ:

№ 507659. Решите уравнение

Решение.

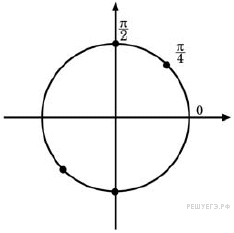Найдем нули числителя:

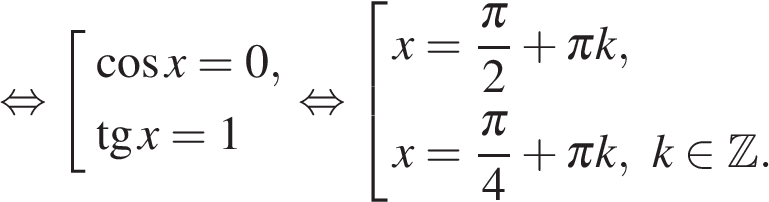
Учитывая, что получаем:

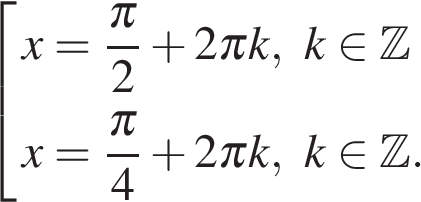
Ответ:

● Итог урока.

10