- Учителю
- Открытый урок по алгебре Логарифмические функции
Открытый урок по алгебре Логарифмические функции
Тема урока: Логарифмическая функция, её свойства и график.
Цели урока.
Образовательные:
-
Ввести понятие логарифмической функции, дать определение.
-
Изучить основные свойства логарифмической функции.
-
Сформировать умение выполнять построение графика логарифмической функции.
-
Научить выявлять свойства логарифмической функции по графику.
Развивающие:
-
Выработать умение выделять главное, сравнивать, обобщать.
-
Формировать графическую и функциональную культуру учащихся.
Воспитательные:
-
Показать взаимосвязь математики с окружающей действительностью.
-
Формировать навыки общения, умения работать в коллективе.
Оборудование:
-
Ноутбук
-
Телевизор
-
Презентация к уроку
-
Презентация учащегося "Логарифмы в окружающем мире"
-
Раздаточный материал
-
Миллиметровая бумага
-
Учебник Алгебра и начала математического анализа 10/Ю.М. Колягин, М.В. Ткачёва, Н. Е. Фёдорова, М.И. Шабунин
Ход урока.
Организационный момент.
Наш урок я хочу начать со слов А.С.Пушкина:
"О, сколько нам открытий чудных
Готовят просвещенья дух
И опыт, сын ошибок трудных,
И гений, парадоксов друг…"
Сегодня вам самим предстоит открыть новые знания. Прежде, чем совершать открытие, давайте проверим себя, готовы ли мы совершить его, всё ли было усвоено на уроках, имеются ли слабые места. Для этого проведём разминку по изученному материалу.
Актуализация.
Устная работа.
1. Учащимся предлагается решить задания устной разминки. Называя координаты ячейки и открывая её, вычисляем логарифмы. В некоторых ячейках есть буквы. После решения всех заданий из этих букв выстраивается фамилия Непер - математик, изобретатель логарифмов (слайд 2,3).
В это время двое учащихся работают по карточкам с тестовыми заданиями.(Ответ НЕПЕР)
На слайде показывается его портрет и краткая справка о нём.
2. Задание на соответствие. У номера графика поставьте букву, соответствующего ему уравнения.
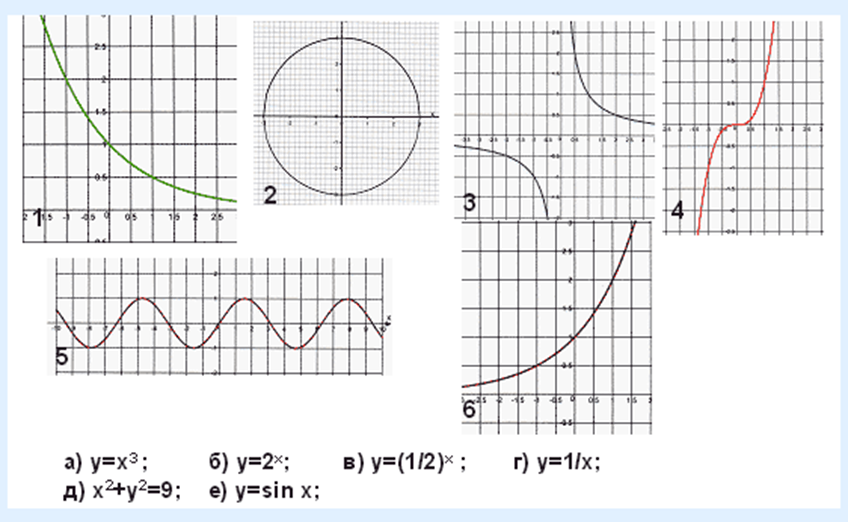



 5
5
![]()
![]()
Задание 3. Вспомните основные этапы исследования функции.
Задание 4. Вычислите, если это возможно:
1 вариант.
2 вариант.
! Если вычислить нельзя, напротив номера выражения поставьте минус.
Затем ученики сверяют ответы по представленным учителем на экране презентации решениям.
Итак, мы повторили необходимый материал. С какими трудностями вы встретились при выполнении самостоятельной работы? (Подводится итог этапа актуализации).
Изложение нового материала.
Возврат к заданиям самостоятельной работы на повторение понятия логарифма.
Задание. Обозначьте изменяющуюся величину через x. При этом значение логарифма тоже будет изменяться. Обозначьте его через y и задайте формулой полученную зависимость y от x.
Итак, ребята, что у вас получилось?
Запись на доске: у= и y =
Задаются ли этими формулами функции?...
Объясните, почему?
Посмотрите внимательно на правую часть формулы.
Подумайте, как бы вы назвали эту функцию?
Объявляется тема урока с записью в тетрадях.
Мотивация.
А находит ли применение эта функция в окружающем нас мире?! А может это просто прихоть математиков?! Наверно нет! Ведь всякое явление можно описать с помощью функции. Давайте убедимся, что и логарифмическая функция находит своё применение.
Об этом нам расскажет ваша одноклассница. Я попросила её подготовить сообщение о том, где встречается логарифмическая функция.
Детская презентация "Логарифмы в окружающем мире".
Нами получено только два примера логарифмической функции:
и .
Их существует множество. Как получить это множество? Возможно, ученики ответят: вместо "2" или "1/2" подставить другие числа. Какие значения могут принимать эти числа? ( больше нуля, не равны 1)
Так какую же функцию мы назовём логарифмической?
Даётся определение логарифмической функции.
На следующем слайде появляется портрет великого математика - Леонарда Эйлера и краткая справка о нём. Учитель задаёт вопрос: Как вы думаете в связи с чем появился портрет этого учёного? Учитель выслушивает варианты ответов и, или подтверждает правильный ответ, или сообщает, что определение логарифмической функции - это заслуга Леонарда Эйлера. Итак, мы сегодня будем изучать логарифмическую функцию.
О чём мы обычно ведём разговор, когда рассматриваем какую-либо функцию?
Возможно ученики ответят:
-
свойства
-
график.
Самостоятельная работа № 2
Постройте по точкам на миллиметровой бумаге графики следующих функций:
1 вариант y = ,
2 вариант у= ,
3 вариант y = ,
4 вариант у= ,
Укажите их свойства (обратите внимание на область определения).
Слабые ученики строят графики 1 и 2 вариантов, для сильных предлагается задание 3 и 4 вариантов.
Работа №1 в группах (4 человека, две соседние парты) с целью взаимопроверки и выработки общего решения. В группе присутствуют ученики разных вариантов. Учитель обращает внимание ребят на то, что свойства зависят от основания.
У некоторых (многих) из вас результаты совпали с моими. Пожалуйста, прокомментируйте, что получили и какими свойствами обладает эта функция ( каждая группа выделяет одного человека по одному графику).
Работа №2 в группах
Задание 1. Исследуйте функцию, заданную формулой y = . Постройте график этой функции в общем виде в зависимости от a.
Задание 2. Сравните результаты своей работы с учебной информацией по данному вопросу в учебнике. Сделайте вывод о проделанной вами работе.
После выполнения задания 1 каждая группа оформляет итог своей работы на плакате. По окончании работы плакаты вывешиваются. Ученики рассматривают, обсуждают итоги работы друг друга. После этого выполняют задание 2.
Динамическая пауза или разрядка для глаз.
Применение знаний, формирование умений и навыков.
На ЕГЭ часто предлагают задания на распознавание графиков функций. Сейчас мы устно выполним такие задания, а заодно, проверим как усвоили новый материал, есть ли ошибки и почему.
Устная работа. Учитель демонстрирует задания на слайдах презентации.
Задание. Какие из следующих графиков не могут быть графиком y = ?
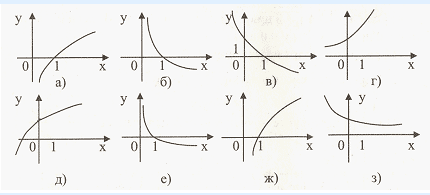
Для остальных определить значение параметра а (а>0,0<a<1).
Задание 2. Найдите наименьшее и наибольшее значения функций на данном промежутке: а), ; б) ,
![]() Правильность
ответа проверяется с помощью презентации (слайд ).
Правильность
ответа проверяется с помощью презентации (слайд ).
Аналогично решается второе задание (слайд ).
Задание 3. Решите уравнения и неравенства:
а) ; б) ; в)
Похожее задание решают самостоятельно, записывая только ответы в тетрадь (слайд ).
Решите уравнения и неравенства: а) ; б) ; в)
Выполняем упр. № 79(1,3), 77(1,3), 78(1,3,5)
Подведение итогов и результатов работы на уроке.
Учитель предлагает учащимся блиц - опрос, чтобы проверить себя, на сколько каждый понял изученный материал (слайд ). Необходимо ответить только «да» или «нет». Проверяется сразу.
Вопросы:
-
Область определения логарифмической функции - вся числовая прямая, а область значений этой функции - промежуток
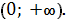
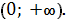
-
Монотонность логарифмической функции зависит от основания логарифма.
-
Не каждый график логарифмической функции проходит через точку с координатами (1; 0).
-
Логарифмическая функция не является ни чётной, ни нечётной.
-
Логарифмическая функция имеет наибольшее значение и не имеет наименьшего значения при а > 1 и наоборот при 0 < a < 1.
Проверка: нет, да, нет, да, нет.
Учитель задаёт вопрос: Каковы результаты? Есть ли учащиеся, которые на все вопросы ответили правильно? У кого только одна или две ошибки? Если есть ученики, у которых больше четырёх ошибок, то не стоит отчаиваться, потому что есть возможность ещё раз дома просмотреть этот материал и найти правильные ответы на вопросы теста.
Итог урока. Домашнее задание. гл.7 § 4, № 74, 82 и 83 по группам .
</ В дополнительной литературе или с помощью Интернет ресурсов постарайтесь найти нерассмотренные на уроке области применения логарифмической функции.
Рефлексия.
6