- Учителю
- Самостоятельная работа по теме 'Средняя линия треугольника и трапеции, пропорциональные отрезки' (8 класс)
Самостоятельная работа по теме 'Средняя линия треугольника и трапеции, пропорциональные отрезки' (8 класс)
Автор публикации: Тихоненкова Е.В.
Дата публикации: 28.02.2015
Краткое описание: Это скорее обучающая самостоятельная работа.Задач много, но они не сложные. Последние 10 - 15 мин. урока отводятся на обсуждение. Условие задачи сразу "рисуем". Дано не записываем. Решение краткое. Все объяснения решений - на обсуждении. Количество заданий избыточно. Даже в с
предварительный просмотр материала
-
Докажите, что если диагонали четырехугольника равны, то середины его сторон служат вершинами ромба. -
Докажите, что если диагонали четырехугольника перпендикулярны, то середины его сторон служат вершинами прямоугольника. -
Через вершины треугольника проведены прямые, параллельные его противоположным сторонам. Докажите, что стороны получившегося треугольника в два раза больше сторон исходного треугольника. -
На сторонах АВ и АС треугольника АВС взяты соответственно точки М и К, причем АМ = 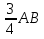 , АК = , АК = 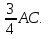 Найдите длину отрезка МК, если ВС = 5. Найдите длину отрезка МК, если ВС = 5. -
Найдите длину отрезка, соединяющего середины диагоналей трапеции, если ее основания равны а и в. -
В трапеции АВСD с основаниями AD и ВС через вершину С проведена прямая, параллельная АВ и пересекающая AD в точке М. Докажите, что в треугольнике DCM две стороны равны боковым сторонам трапеции, а третья сторона равна разности ее оснований. -
Данный отрезок разделите на три равные части. -
На одной стороне угла расположены два отрезка длиной 3и 4. Через их концы проведены параллельные прямые, образующие на другой стороне также два отрезка. Длина большего из отрезков равна 6. Найдите длину другого отрезка. -
В трапеции ABCD боковая сторона АВ равна 5, а основание ВС равно 4. Какую из сторон трапеции, ВС или CD, пересекает биссектриса угла А этой трапеции
|
|
-
Докажите, что если диагонали четырехугольника равны, то середины его сторон служат вершинами ромба. -
Докажите, что если диагонали четырехугольника перпендикулярны, то середины его сторон служат вершинами прямоугольника. -
Через вершины треугольника проведены прямые, параллельные его противоположным сторонам. Докажите, что стороны получившегося треугольника в два раза больше сторон исходного треугольника. -
На сторонах АВ и АС треугольника АВС взяты соответственно точки М и К, причем АМ = 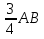 , АК = , АК = 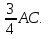 Найдите длину отрезка МК, если ВС = 5. Найдите длину отрезка МК, если ВС = 5. -
Найдите длину отрезка, соединяющего середины диагоналей трапеции, если ее основания равны а и в. -
В трапеции АВСD с основаниями AD и ВС через вершину С проведена прямая, параллельная АВ и пересекающая AD в точке М. Докажите, что в треугольнике DCM две стороны равны боковым сторонам трапеции, а третья сторона равна разности ее оснований. -
Данный отрезок разделите на три равные части. -
На одной стороне угла расположены два отрезка длиной 3и 4. Через их концы проведены параллельные прямые, образующие на другой стороне также два отрезка. Длина большего из отрезков равна 6. Найдите длину другого отрезка. -
В трапеции ABCD боковая сторона АВ равна 5, а основание ВС равно 4. Какую из сторон трапеции, ВС или CD, пересекает биссектриса угла А этой трапеции |
|