Урок 'Показательные уравнения и способы их решения' (10 класс)

Конспект урока по теме

«Виды показательных уравнений и методы их решения».

Метод решения хорош, если с самого начала

мы можем предвидеть - и далее подтвердить это, - что,

следуя этому методу, мы достигнем цели.

(Г. Лейбниц)

Цели урока:

• Закрепить понятие простейшего показательного уравнения.

• Систематизировать и уметь применять методы решения показательных уравнений.

• Показать практическую значимость формулы.

Задачи:

• Содействовать развитию математического мышления учащихся.

• Побуждать учащихся к преодолению трудностей в процессе умственной деятельности.

Оборудование: персональные компьютеры мобильного класса.

Тип урока: урок изучения нового материала с применением ИКТ.

Вид урока: работа в группах .

Этапы урока :

1. Организационный момент.

2. Проверка домашнего задания.

3. Объяснение новой темы.

4. Закрепление темы.

5. Задание на дом. Итог урока.

Класс разбит на группы, в которых есть слабые и сильные ученики, каждая группа получила домашнее задание: по внешнему виду показательных уравнений разделить их на группы.

Ход урока:

1. Этап урока.

Здравствуйте, ребята. Сегодня мы продолжаем решать показательные уравнения, правда, вы заметили из домашней работы, что они немного сложнее. Работать будем в группах постоянного состава, каждая группа выполнила творческое задание, которое пригодится нам в процессе урока.

2. Этап урока

Лидеры групп предлагают свою версию по классификации показательных уравнений, происходит обсуждение, если есть разногласия между выбором групп.

Приходим к единому мнению:

Метод приведения к одному основанию.

Метод замены переменной

Метод почленного деления (однородные уравнения).

Графический метод

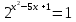
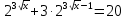
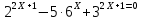
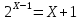
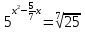
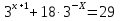
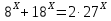
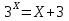
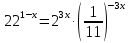
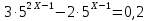
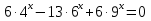
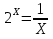
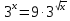
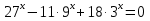
Привести к одному основанию.

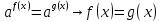
Одинаковую степень заменить новой переменной, получится линейное, или квадратное, или дробно-рациональное уравнение.

Не забыть вернуться к исходной переменной.

Разделить обе части уравнения на одну из степеней данного уравнения.

Построить графики известных функций, найти координату х точек пересечения, проверить это значение для данного уравнения.

Все эти уравнения взяты из материалов ЕГЭ. Какие уравнения умеете решать?

Уравнения 1 столбика решать умеем.

У доски 4 человека решают уравнения 1 столбика. Эти уравнения относятся к классу уравнений, решаемых методом приведения к одному основанию. Основная задача при решении любого показательного уравнения: привести степени с переменным показателем к одному основанию.

Как быть с остальными уравнениями?

Такие уравнения нужно научиться решать.

3. этап урока

Объявляется цель урока: знать методы решения показательных уравнений, знать характерные признаки уравнений каждого типа.

Какие характерные признаки уравнений 2 столбика?

Степени приводятся к одинаковому основанию, есть числовое слагаемое и несколько слагаемых, содержащих степени с разными показателями. Метод решения: одинаковую степень заменить новой переменной, получится линейное, или квадратное, или дробно-рациональное уравнение.

Не забыть вернуться к исходной переменной.

Решить уравнения. По ходу урока заполняется таблица.(слайд на компьютере)

1)

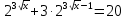
Пусть 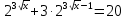, тогда уравнение примет вид t+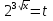, t=8

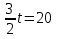, х=1. Ответ: 1.

2)

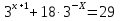
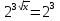
Пусть 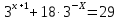, тогда 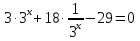т.к. у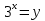то уравнение равносильно 3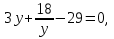

У=9 или у=.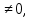

, ,

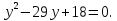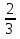Х=2 х =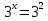

Ответ: 2,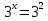

3) Третье уравнение из столбика 2 решить в домашней работе.

Какие характерные признаки уравнений столбика 3?

Данные уравнения нельзя привести к одинаковому основанию, но можно привести к одинаковому показателю. Метод решения: разделить обе части уравнения на одну из степеней данного уравнения.

4)

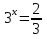
2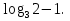, разделим на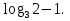

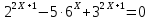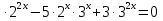Пусть тогда уравнение примет вид :

2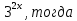

Корни уравнения у=1, у =.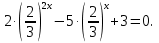

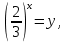
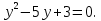
Х=0 х=-1.

Ответ: -1; 0.

5). Второе уравнение столбика 3 выполнить самостоятельно.

Ответ проверить, вопросы разобрать. Ответ: 0.

Каким характерным качеством обладают уравнения 4 столбика?

Уравнения состоят из показательной функции и какой -либо ещё, в данных случаях это линейная функция и функция обратной пропорциональности. Метод решения: построить графики известных функций, найти координату х точек пересечения, проверить это значение для данного уравнения.

Нужно отметить, что данный метод не всегда дает точное значение корня, поэтому данный метод применяется при решении уравнений с вопросом: Сколько корней имеет уравнение?

6)

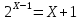
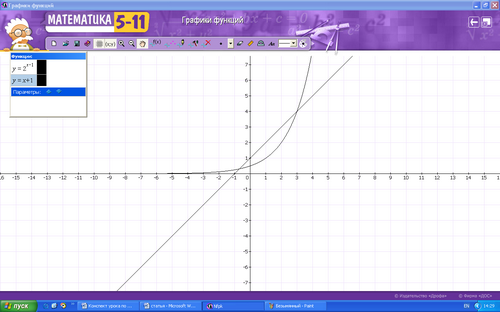
Ответ: х=3; х.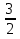

7) Сколько корней имеет уравнение
?

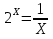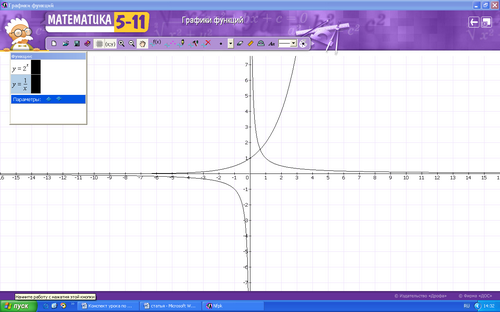
Ответ: уравнение имеет один корень.

8). Решение оставшегося уравнения 4 столбика выполните в программе НФПК на компьютере. Проверяем сразу .

4. этап урока.

Самостоятельная работа по группам.(слайд на компьютере)

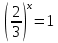
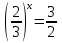
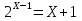
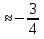Ответы: 2

-1;3

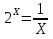
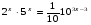
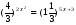
Ответы:

2

4

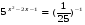
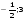
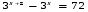
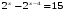
Ответы: 4

1

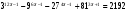
5. этап урока.

Домашнее задание: подобрать по два уравнения из сборников для подготовки к ЕГЭ к каждому типу уравнений и решить их. Для чего нужны такие уравнения?