- Учителю
- Три урока по теме: «Решение треугольников».
Три урока по теме: «Решение треугольников».
МАОУ ЛИЦЕЙ №44 г. Липецка
Учитель математики: Скорикова Людмила Алексеевна.
Уроки математики в 11 классе
(социально-экономический профиль)
Задачи с параметрами
по теме: Иррациональные уравнения и неравенства.
Решение задач с параметрами с применением производной.
Цель: повысить уровень подготовленности учащихся к сдаче Единого Государственного Экзамена по математике.
Пояснительная записка.
Предлагаемая система занятий расширяет и углубляет базовую основу общеобразовательной программы по математике и ориентирована на повышение уровня подготовленности учащихся к сдаче ЕГЭ.
Задачи с параметрами представляют для учащихся наибольшую сложность. Это самые трудные задания и на выпускных экзаменах и на вступительных экзаменах в ВУЗ.
Решению задач с параметрами в школе уделяется мало внимания. Устранить этот пробел можно на внеклассных занятиях.
Универсальных указаний по решению задач с параметрами дать нельзя. При решении задач с параметрами приходится рассматривать различные случаи, в зависимости от значений параметров, и методы решения задач различны. Но задание некоторых правил и алгоритмов решения необходимо.
Взяты эти задания из различных источников. Большинство из этих заданий полагалось на вступительных экзаменах в ВУЗах.
В пособии даются краткие теоретические сведения, задания с параметрами по основным разделам алгебры.
Пособие содержит 187 заданий, большая часть из которых имеет решение. Используются аналитические и графические способы решения уравнений и неравенств.
Некоторые задания предлагается решить различными способами.
Рассматриваются 10 тем, в конце каждой даются задания для самостоятельной работы.
Обращаться к решению стоит только после того, как самостоятельно эти задания будут решены или когда Вы не в силах самостоятельно справиться с ними.
Данное пособие может быть полезным учителям математики, абитуриентам, школьникам.
Иррациональные уравнения и неравенства
I Иррациональные уравнения.
При решении иррациональных уравнений с параметрами пользуются общими формулами. Пусть f и q - некоторые функции, 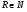 , тогда:
, тогда:
1). 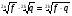 , f ≥ 0; q ≥ 0.
, f ≥ 0; q ≥ 0.
2). 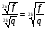 , f ≥ 0; q > 0.
, f ≥ 0; q > 0.
3). 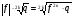 , q ≥ 0.
, q ≥ 0.
4). 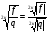 ,
, 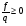 , q ≠ 0.
, q ≠ 0.
5). 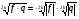 , fq ≥0.
, fq ≥0.
Применяя эти формулы нужно иметь в виду, что ОДЗ левой и правой частей каждой из них могут быть различными. Для каждой формулы ОДЗ правой части может быть шире ОДЗ левой.
Отсюда следует, что преобразования уравнения с формальным использованием формул «слева-направо» приводят к уравнению, являющемуся следствием исходного. В этом случае могут появиться посторонние корни уравнения.
Преобразование уравнений с формальным использованием данных формул «справа-налево» недопустимы, т.к. возможно сужение ОДЗ исходного уравнения, а следовательно, и потеря корней.
Уравнение вида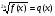 ,
, 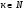 равносильно системе:
равносильно системе:
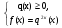
Пример 1.
Решить уравнение 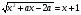 .
.
Решение.
Заданное уравнение равносильно системе6
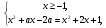 =>
=> 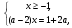 =>
=>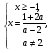
Находим а, при которых 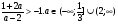
Ответ: 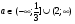
Пример 2.
Решить уравнение 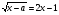 .
.
Решение.
Заданное уравнение равносильно системе
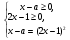 =>
=> 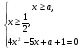
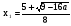 ,
, 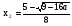
х1, х2 являются действительными числами при а ≤ 9/16. При а > 9/16 решений нет.
Удовлетворим неравенства х ≥ а и х ≥ ½.
а) 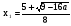 ≥ ½
≥ ½
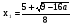
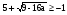 ≥ а
≥ а
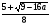
Если а ≤ 9/16, то 8а-5<0 и неравенство 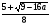 справедливо при всех допустимых а.
справедливо при всех допустимых а.
б). 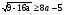
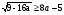 а ≥ ½ (а ≤ 9/16)
а ≥ ½ (а ≤ 9/16)
Следовательно, х2 является решением исходного уравнения при ½ ≤ а ≤ 9/16
Ответ: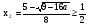 , если а < ½;
, если а < ½; , если ½ ≤ а ≤ 9/16; нет решений, если а>9/16.
, если ½ ≤ а ≤ 9/16; нет решений, если а>9/16.
Пример 3.
Решить уравнение 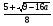
Решение.
ОДЗ: х - а ≥ 0, х ≥ а
х1 = 1, х2 = а
Если а = 1, то х1 = х1 = 1.
Если а < 1, то х1 = 1 удовлетворяет условию ОДЗ х ≥ а, т.е. является корнем уравнения.
Если а > 1, то х1 = 1 не удовлетворяет условию х ≥ а, т.е. является посторонним корнем.
Ответ: 1) если а < 1; то х1 = 1; х2 = а; 2) если а ≥ 1, то х = а.
Пример 4.
При каких а уравнение 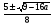 имеет один корень?
имеет один корень?
Решение.
х1 = 4, х2 = а
Корень будет единственным, если а=4; если одно из двух значений (4 и а) является посторонним корнем, а именно х = а. Это произойдет при условии, что х = а не входит в область определения уравнения х ≥ 0, т.е. при а < 0.
Ответ: а = 4 или а < 0.
Пример 5.
Найти минимальное целое положительное значение параметра а, при котором уравнение 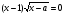 имеет различные положительные корни.
имеет различные положительные корни.
Решение.
ОДЗ:
ах -8 ≥ 0, х ≥ 8/а, х > 0, а > 0
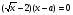
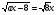
D = 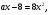
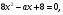
а >16 (а < -16 не входит в ОДЗ)
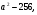 ,
, 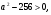 . А = 17 - минимальное целое число.
. А = 17 - минимальное целое число.
Ответ: 17.
Пример 6.
Найти все значения параметра а, при которых корни уравнения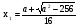 принадлежат отрезку [2;17].
принадлежат отрезку [2;17].
Решение.
Пусть 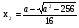
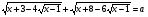 , t ≥ 0, х - 1 = t2
, t ≥ 0, х - 1 = t2
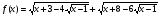 ,
,
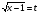 ,
,
|t - 2| + |t - 3| = а
1) 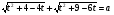 =>
=> 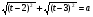 =>
=> 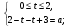 =>
=> 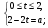
2) 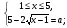 =>
=> 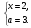 =>
=> 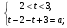
3) 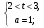 =>
=> 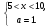 =>
=> 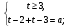 =>
=> 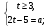
Ответ: 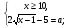 .
.
Пример 7.
Решить уравнение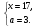 .
.
Решение.
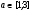 х ≥ 2
х ≥ 2
(х + 1)(х - 2) = а; х2 - х - 2 = а, х2 - х - 2 - а = 0.
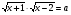 ,
, 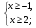 .
.
Множеству х ≥ 2 принадлежит только корень х2.
Ответ: при а ≥ 0 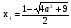 .
.
Пример 8.
Решить уравнение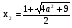 .
.
Решение.
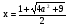 . Так как
. Так как 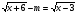 , то m > 0. Пусть у =
, то m > 0. Пусть у = 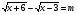 , тогда х = у2 + 3, и исходное уравнение равносильно системе уравнений:
, тогда х = у2 + 3, и исходное уравнение равносильно системе уравнений:
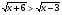 т.е.
т.е. 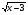 <=>
<=> 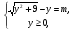 <=>
<=> 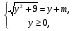 ,
,
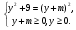 ,
, 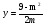 ,
, 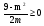 .
.
Ответ: при m < 0, m>3 решений нет, при 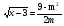
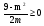 .
.
Пример 9.
Решить уравнение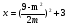 .
.
Решение.
Пусть 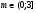 , тогда
, тогда 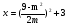 ,
,
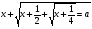 ,
, 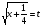 , а т.к. t > 0, то
, а т.к. t > 0, то 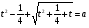 ,
,
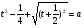 ,
, 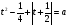 ,
, 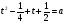 . ( а > ¼)
. ( а > ¼)
х = 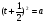 .
.
Ответ: х = 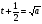 при а > ¼.
при а > ¼.
Пример 10.
Найти все значения параметра а, при которых уравнение 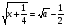 имеет решение.
имеет решение.
Решение.
Если изобразить графики функций 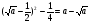 и
и 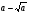 , то очевидно, что они пересекаются (и исходное уравнение имеет решение) при
, то очевидно, что они пересекаются (и исходное уравнение имеет решение) при 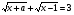 .
.
1
у
х
-а а 1 -а 10=-а
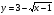
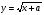
3
Пример 11.
При каких а решением неравенства 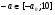 является промежуток [2;18)?
является промежуток [2;18)?
Решение.
ОДЗ: 3 - а > 0, а < 3.
х - 2 < (3 - а)2,
х < (3 - а)2 +2,
х < 11 - 6а +а2, т.к.  , то
, то
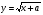
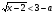
а = -1.
а = 7 - не подходит в ОДЗ.
Ответ: а = -1.
Пример 12.
Решить неравенство 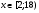 , где а - параметр.
, где а - параметр.
Решение.
При любом значении а, если правая часть х + а - 1 < 0, т.е. х < 1 - а, заданное неравенство справедливо.
При х ≥ 1 - а равносильная система имеет вид :
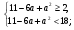 =>
=> 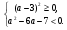 (*)
(*)
Рассмотрим возможные случаи:
-
Если а > 1, то 1 - а ≤ х <
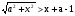 . Объединяя с множеством х < 1 - а, получим х <
. Объединяя с множеством х < 1 - а, получим х < 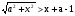 .
. -
Если а = 1, то х ≥ 1 - решение системы (*). Объединяя с множеством х< а - 1 (а = 1), находим: х - любое число.
-
Если а < 1, то решение системы (*) х ≥ 1 - а. Присовокупив х < 1 - а, имеем: х - любое число.
Ответ: 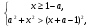 , если а > 1;
, если а > 1; 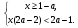 , если а ≤ 1.
, если а ≤ 1.
Пример 13.
Решить уравнение 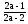
Решение.
ОДЗ:
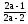
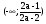
Из данного уравнения следует:
1 - х2 = х2 + 2ах + а2,
2х2 + 2ах + а2 - 1 = 0.
D/4 = 2 - а2. D > 0 при |a| <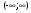 .
.
Затем если изобразить графики функций 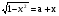 и
и 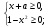 , то видно как меняется количество решений в зависимости от а.
, то видно как меняется количество решений в зависимости от а.
у
х
-1
1
-1
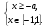
у = а + х
Ответ: при нет решений; при
нет решений; при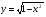 и
и 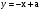 одно решение; при
одно решение; при  два решения.
два решения.
Задание на дом:
1). Решить уравнение 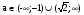 .
.
Ответ: 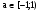 .
.
2). Найти левый и правый края области значений параметра а, в которой уравнение 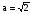 имеет различные положительные корни.
имеет различные положительные корни.
Решение.
ОДЗ:
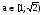
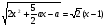 , х > 0, а ≥ 0.
, х > 0, а ≥ 0.
7х - а = ах2,
ах2 - 7х + а = 0,
D = 49 - 4a2 > 0
а = -3, 5 не входит в ОДЗ.
Ответ: 0 и 3,5.
3). Решить уравнение 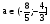 .
.
Решение.
Данное уравнение равносильно системе:
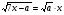 =>
=> 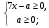
При а = 2 второе уравнение имеет вид 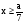 , т.е.
, т.е. 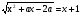 .
.
При а ≠ 2 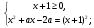 .
.
Выясним при каких значениях а найденное значение х удовлетворяет неравенству х ≥ -1.
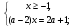
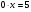 .
.
Ответ: при а ≤ 1/3 и а > 2 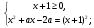 ; при 1/3 < а ≤ 2 уравнение не имеет решений.
; при 1/3 < а ≤ 2 уравнение не имеет решений.
4). Найти все значения параметра а, при которых корни уравнения 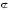 принадлежит отрезку [-4;44].
принадлежит отрезку [-4;44].
Ответ: 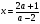 .
.
5). При всех а решить неравенство 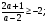 .
.
Решение.
ОДЗ: 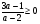
а). Если а ≤ 0, то данное неравенство справедливо при всех 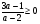 .
.
б). Если а > 0, то данное неравенство равносильно системе неравенств.
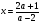
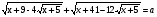 =>
=> 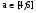 .
.
Ответ: при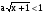
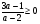 ; при
; при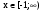
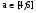 .
.
Решение задач с параметрами с применением производной.
Пример1.
При каком значении параметра а касательная к графику функции 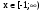 в точке х = 1 образует с осью х угол 135°?
в точке х = 1 образует с осью х угол 135°?
Решение.
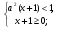 ;
;
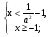 , т.к. tg135°=-1.
, т.к. tg135°=-1.
2ах + 5 = -1;
а = -3.
Ответ: а = -3.
Пример 2.
При каком наибольшем значении а функция 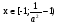 возрастает на всей числовой прямой?
возрастает на всей числовой прямой?
Решение.
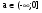
D/4 < 0.
D/4 = а2 - 14а ≤ 0,
а(а-14) ≤ 0.
--14
а
0
+
+
Ответ: 14.
Пример 3.
При каких значениях параметра а функция 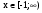 возрастает на всей числовой прямой?
возрастает на всей числовой прямой?
Решение.
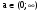
D/4 ≤ 0.
D/4 = (3а)2 - 18а=9а2 - 18а = 9а(а - 2).
2
а
0
+
+
Ответ: 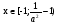 .
.
Пример 4.
При каких а точка х0=а является точкой минимума функции 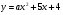 ?
?
Решение.
D(у)=D(у/)=R.
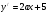 ,
,
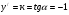 ,
,
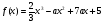 ,
,
D = (а - 1)2 ≥0.
х1=1; х2=а.
-1). а < 1.
1
у
а
+
+
у/
Max
Min
х0=2 - max
2). а = 1.
у
а=1
+
+
у/
6(х-1)2=0
3). а > 1.
-а
у
1
+
+
у/
Max
Min
6(х-1)(х-а)=0
х0=а - min
Ответ: при а > 1.
Пример 5.
При каком натуральном значении параметра а уравнение 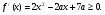 имеет ровно два корня?
имеет ровно два корня?
Решение.
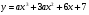 .
.
С помощью производной строим график 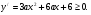 .
.
1
у
у = а
-3
-5
х
27
Ответ: а = 27.
Пример 6.
Найти все возможные значения а, при которых наименьшее значение функции 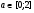 на отрезке [0;а] достигается в правом конце отрезка.
на отрезке [0;а] достигается в правом конце отрезка.
Решение.
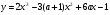 при х = ± 2. Это критические точки.
при х = ± 2. Это критические точки.
2
у
-2
+
+
у/
0
f(0)=0, f(2)=16,
f(a)=a3-12f
-
Если о < а < 2, то f(a) < 0 и принимает наименьшее значение в правом конце, что и требуется. Критических точек на отрезке нет.
Если а = 2, то критическая точка (min) совпадает с правым концом отрезка.
а
0
2
Это удовлетворяет условию.
Если а > 0, то f(a) = a3 - 12a = a(a2 - 12) > 2(4 - 12) > -16 = f(2),т.е. наименьшее значение принимает во внутренних точках отрезка, а не в его конце.
Ответ: 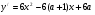
Пример 7.
Найти все значения параметра а, при которых функция 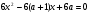 возрастает при любом
возрастает при любом 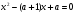 .
.
Решение.
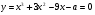 .
.
Чтобы 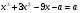 была ≥ 0, требуется выполнение двух условий в системе:
была ≥ 0, требуется выполнение двух условий в системе:
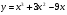 =>
=> 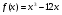
Ответ: 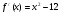
Пример 8.
При каких в и с прямые у = х и у = -2х являются касательными к графику функции у = х2 + вх + с?
Решение.
Пусть t - абсцисса точки касания прямой у = х с параболой у = х2 + вх + с; р - абсцисса точки касания прямой у = -2х с параболой у = х2 + вх + с.
Тогда уравнение касательной у = х примет вид у = (2t + в)х +с - t2, а уравнение касательной у = -2х примет вид у = (2р + в)х +с +р2.
Составим и решим систему уравнений:
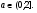 =>
=> 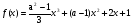
Ответ: 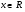
Пример 9.
Найти все а, при котором уравнение 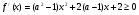 имеет три корня.
имеет три корня.
Решение.
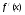
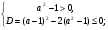
а ≠ 0, D1 = 36, х1 = ½, х2 = ½ + 3/а.
Чтобы уравнение имело три корня, достаточно, чтобы значения функции в точках экстремума имели различные знаки, т.е. f(х1)·f(х2) < 0.
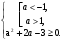
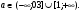
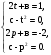
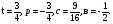
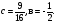
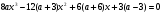
-3
0
+
+
а
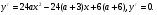 .
.
Ответ: 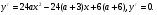 .
.
Пример 10.
Найти все значения параметра а, при которых выражение (х1-5х2)(х2-5х1), где х1 и х2 - действительные корни квадратного трехчлена х2 + ах + а - 0,5, принимает наибольшее значение. В ответе записать найденное значение параметра, а если таких значений несколько, то их сумму.
Решение.
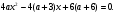
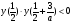 .
.
Пусть 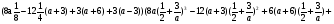
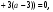 f(x) = 0 при а = 3,6.
f(x) = 0 при а = 3,6.
а
f(x)
3,6
-
+
f/(x)
Max
Ответ: 3,6.
Пример 11.
Найти все значения а, при которых касательная к графику функции 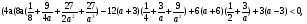 в точке графика с абсциссой а не пересекает график ни одной их двух функций: у = 0,5х + 2 и у = -2/х.
в точке графика с абсциссой а не пересекает график ни одной их двух функций: у = 0,5х + 2 и у = -2/х.
Решение.
Пусть 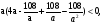 Т.к. касательная к графику функции
Т.к. касательная к графику функции 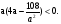 не пересекается с прямой
не пересекается с прямой 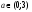 , то она ей параллельна, т.е. ее угловой коэффициент равен 0,5.
, то она ей параллельна, т.е. ее угловой коэффициент равен 0,5.
Угловой коэффициент касательной, проведенной к графику 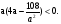 через его точку с абсциссой х0, равен значению производной функции f(x) в точке х0, т.е. f/(x)=0,5.
через его точку с абсциссой х0, равен значению производной функции f(x) в точке х0, т.е. f/(x)=0,5.
Функция f(x)дифференцируема на R и ее производная равна 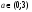 Или
Или 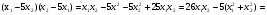
Но если 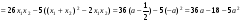 , то
, то 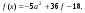 и значение функции f(x) в точке х0 равно 1,5а - а2.
и значение функции f(x) в точке х0 равно 1,5а - а2.
Уравнение касательной проведенной к графику 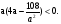 через его точку с абсциссой х0, имеет вид:
через его точку с абсциссой х0, имеет вид: 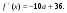
По условию х0 = а, значит уравнение касательной можно переписать в виде 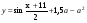
Из равенства 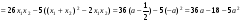 (формально подставляем а вместо х0), находим, что а может иметь вид
(формально подставляем а вместо х0), находим, что а может иметь вид 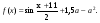
Воспользуемся теперь тем, что касательная 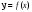 не пересекает график у = -2/х.
не пересекает график у = -2/х.
Это означает, что уравнение 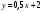 не имеет решений. Приведем последнее уравнение к квадратному
не имеет решений. Приведем последнее уравнение к квадратному 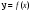 .
.
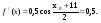
Квадратное уравнение не имеет решений, если D<0, т.е. 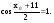 , т.е. -1< а < 2.
, т.е. -1< а < 2.
Поскольку 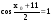 имеем неравенство
имеем неравенство 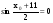 , откуда
, откуда 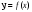 .
.
Т.к. 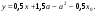
Итак, единственным значением а, удовлетворяющим условиям задачи, является 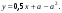
Ответ: а =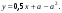
Домашнее задание.
-
При каком наибольшем значении m функция
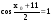 убывает на всей числовой прямой?
убывает на всей числовой прямой?
Ответ: 6.
-
При каком наименьшем целом значении параметра р уравнение
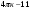 имеет три корня?
имеет три корня?
Ответ: -7.
-
Найти все значения параметров в и с, при которых прямая у = 2х + 2в касается параболы f(х)=х2 + вх + с в точке (2;0).
Решение.
Т.к. точка (2;0) лежит на графике f(x)=х2 + вх + с, то 0 = 4 + 2в + с;
f/(x) = 2х + в; f/(2) = 4 + в=2.
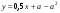 => в = -2, с = 0.
=> в = -2, с = 0.
Ответ: в = -2, с = 2.
-
При каких значениях а функция
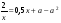 имеет минимум в точке х=3?
имеет минимум в точке х=3?
Решение.
у/ = 6х2 - 6а2 = 6(х - а)(х + а)
Рассмотрим 2 случая:
1). а = 0 у/ = 6х2 ≥ 0 для любого х, функция возрастает на 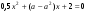 .
.
2). а ≠ 0. Знаки производной:
-
-а
-а
+
+
х
-а
а
+
+
х
а = 3. -а = 3, а = -3.
Ответ: а = ± 3.
-
При каких значениях р касательная, проведенная к графику функции у=х3-рх в точке с абсциссой х0=1, проходит через точку М (2;3)?
Решение.
у/ = 3х2 - р
укас=(3х02 - р)(х - х0) + х03-рх0,
3 = (3 - р)(2 - 1) +1 - р,
3 = 3 - р + 1 - р, 2р = 1, р = ½.
Ответ: р = ½.