- Учителю
- Конспект урока по геометрии на тему 'Решение планиметрических задач методом площадей'
Конспект урока по геометрии на тему 'Решение планиметрических задач методом площадей'
Муниципальное общеобразовательное учреждение - гимназия № 1
Урок геометрии в 11 классе
Тема: «РЕШЕНИЕ ПЛАНИМЕТРИЧЕСКИХ ЗАДАЧ
МЕТОДОМ ПЛОЩАДЕЙ»
Автор: Дацко Елена Владимировна
учитель математики
г. Клин, 2014 год
Содержание
Стр.
1. Цель и задачи урока………………………………………………………………………...…3
2. План урока……………………………………………………………………………..…3 - 11
2.1. Актуализация знаний……………………………………………………………………3 - 4
2.2. Устная работа………………………………...………………………………………….5 - 7
2.3. Работа на уроке по вариантам с различной сложностью……………………………..7 - 9
2.4. Самостоятельная работа контролирующего характера……………………………10 - 11
2.5. Итог урока. Домашнее задание с подробным разбором задач....……………….…11 - 17
3. Литература……………………………………………………………………………………18
Слайд 2
Цель урока: повторение и обобщение знаний о методе площадей в решении задач.
Задачи:
- обучающие: обобщить и систематизировать знания о методе площадей, отработать умения применить формулы в решении задач.
- развивающие: развить познавательные умения,
- воспитательные: развить положительное отношение к знаниям.
Тип урока: урок повторения.
Ход урока
I. Актуализация знаний.
Слайд 3
Площади треугольников, имеющих равные высоты (общую высоту), относятся как стороны соответствующие этим высотам.
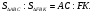
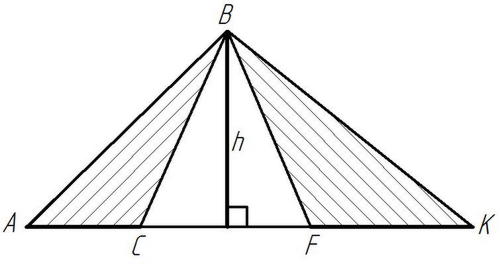
Рисунок 1
Слайд 4
Площади треугольников, имеющих равные стороны, относятся как соответствующие этим сторонам высоты.
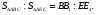
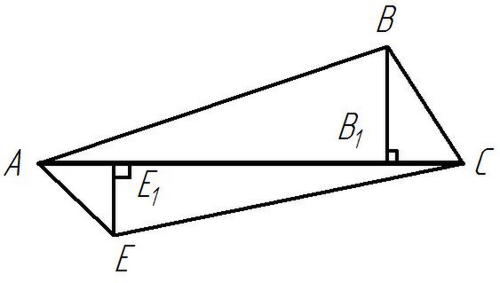
Рисунок 2
Слайд 5
Площади треугольников, имеющих равный угол (или общий угол), относятся как произведение сторон, содержащий этот угол.
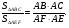
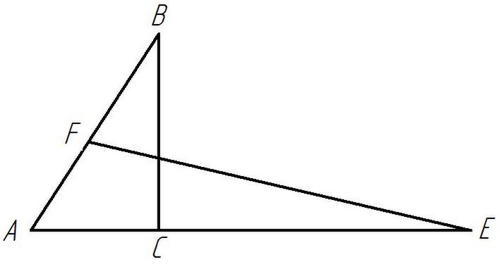
Рисунок 3
Слайд 6
Медиана делит треугольник на два равновеликих треугольника.
Три медианы треугольника делят его на шесть равновеликих треугольников.
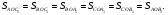
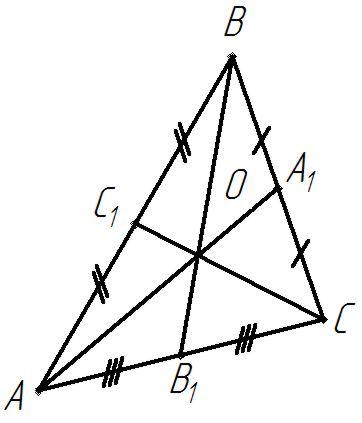
Рисунок 4
Слайд 7
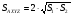
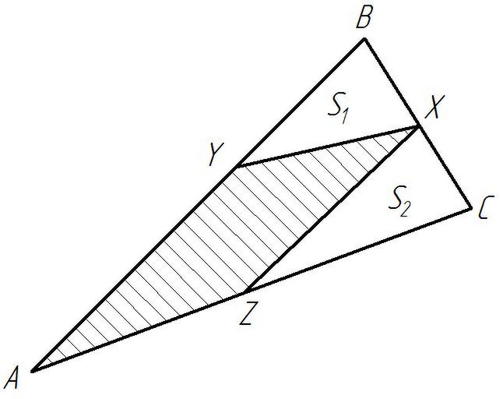
Рисунок 5
II. Устная работа.
Слайд 8 Случай, когда треугольники имеют общую высоту.
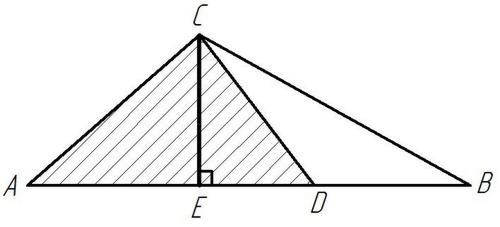
Рисунок 6
Дано:
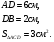
Найти:
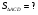
Решение:
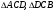 имеют общую высоту
имеют общую высоту 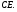
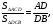
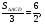
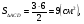
Ответ: 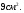
Слайд 9
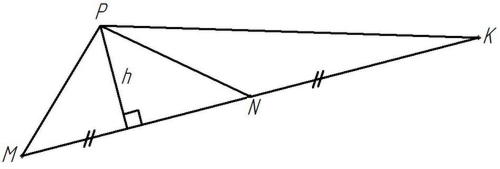
Рисунок 7
Дано:
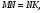
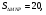
Найти:
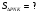
Решение: 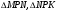 имеют общую высоту
имеют общую высоту 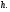
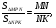 т. к.
т. к. 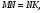 то
то 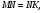
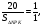
Ответ: 20.
Вывод:
1) Отношение площадей треугольников, имеющих общую высоту равно отношению сторон, к которым проведена высота.
2) Если же стороны, к которым проводится высота равны, то и площади треугольников также равны.
3) Во сколько раз отношение сторон треугольников, к которым проводится высота больше (меньше), во столько раз и площади больше (меньше).
Слайд 10
Случай, когда треугольник и параллелограмм имеют общую высоту.
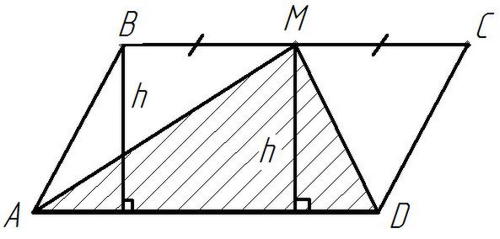
Рисунок 8
Дано:
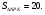 параллелограмм,
параллелограмм,
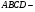
Найти:
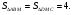
Решение: 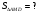
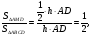
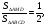
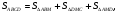
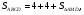
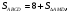
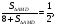
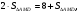
Ответ: 8.
Вывод: В этом случае отношение площадей треугольника и параллелограмма равно отношению их высот. Высота параллелограмма есть высота треугольника. Но в нахождении площади треугольника присутствует коэффициент 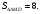 , а, значит, составляя и решая данную пропорцию, получаем 8.
, а, значит, составляя и решая данную пропорцию, получаем 8.
Слайд 11
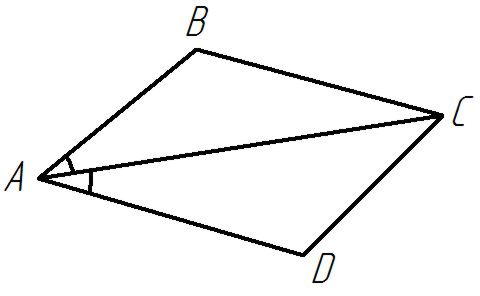
Рисунок 9
Дано:
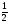
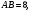
Найти:
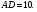
(Отношение площадей, имеющих общий угол равно отношению произведения сторон, заключающих данный угол).
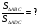 - общая,
- общая, 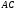
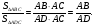
Ответ: 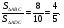
Слайд 12
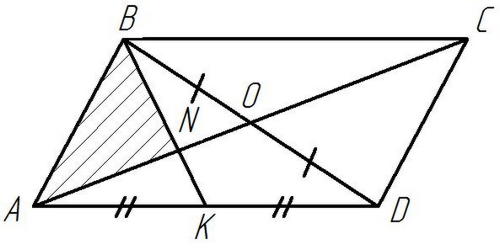
Рисунок 10
Дано:
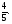 - параллелограмм,
- параллелограмм,
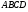 - медиана
- медиана 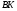
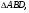 - медиана
- медиана 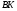
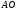 - середина
- середина 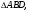
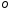
Найти:
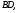
Решение:
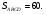
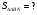
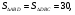
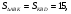
Ответ: 10.
III. Работа на уроке.
1 ряд. Работа в парах (сидят слабый ученик и ученик средних способностей).
Решает I вариант - уровень «4»,
2,3 ряды - II вариант - уровень «4 - 5».
I вариант
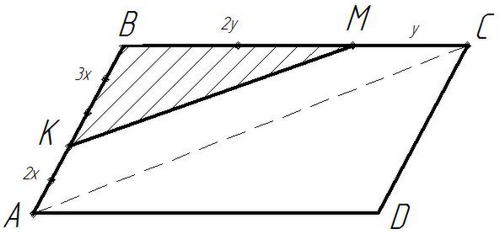
Рисунок 11
Дано:
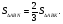 - параллелограмм,
- параллелограмм,
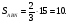
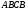
Найти:
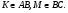
Решение:
1) Найдём какую часть 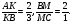 составляет от
составляет от 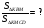
Проведём диагональ 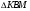
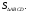 (общий угол
(общий угол 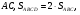 ),
),
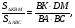
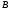
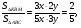
2) 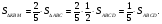
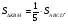
3) 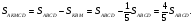
Ответ: 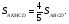
II вариант
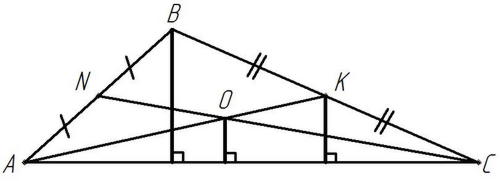
Рисунок 12
Дано:
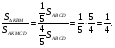
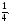 - медианы,
- медианы,
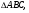
Найти:
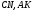
Решение:
1) 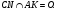 (сторона
(сторона 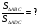 - общая),
- общая),
2) Дополнительное построение 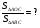
По теореме Фалеса 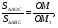 - средняя линия,
- средняя линия,
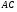
3) 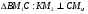 подобен
подобен 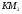 (по двум углам),
(по двум углам),
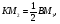 - коэффициент подобия.
- коэффициент подобия.
4) по свойству медиан 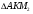
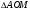
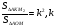
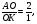
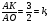
подставим в 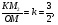 получим
получим 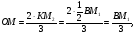
Ответ: 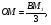
IV. Самостоятельная работа контролирующего характера (дифференцированная).
1 ряд
I вариант
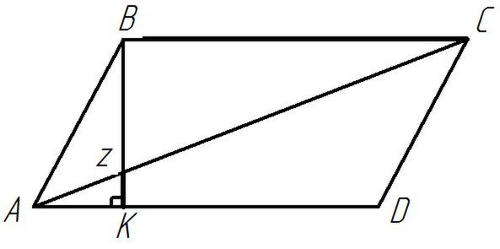
Рисунок 13
Дано:
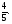 - параллелограмм,
- параллелограмм,
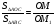
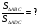 - диагональ,
- диагональ,
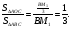
Найти:
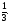
Решение:
Параллелограмм 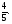 и
и 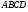 имеют общую сторону
имеют общую сторону 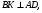
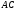
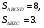
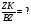
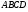
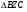
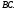
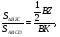
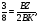
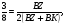
Ответ: 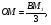
II вариант
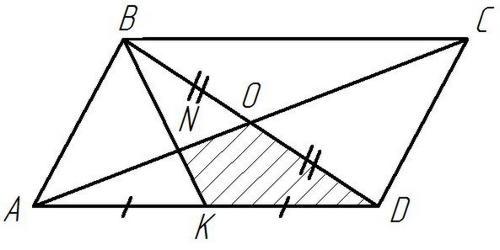
Рисунок 14
Дано:
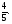 - параллелограмм,
- параллелограмм,
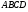 - медиана,
- медиана,
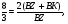
Найти:
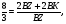
Решение:
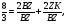 - медианы,
- медианы, 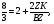
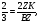 (свойство диагоналей),
(свойство диагоналей),
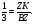
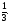 - общий,
- общий,
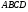
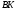
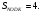 имеют общую высоту, значит их площади
имеют общую высоту, значит их площади 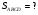
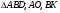
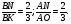
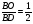
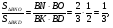
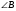
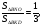
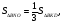
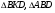
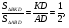
Ответ: 24.
V. Итог урока.
Домашнее задание. Ученику следует выбрать для решения две любые задачи. При желании можно выполнить всё задание.
Задача 1. В треугольнике 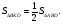 со сторонами
со сторонами 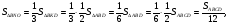 вписан параллелограмм
вписан параллелограмм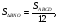 причём точки
причём точки 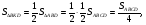 лежат на сторонах
лежат на сторонах 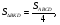 соответственно. Известно, что площадь параллелограмма составляет
соответственно. Известно, что площадь параллелограмма составляет 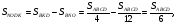 площади треугольника
площади треугольника 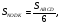 Найдите стороны параллелограмма.
Найдите стороны параллелограмма.
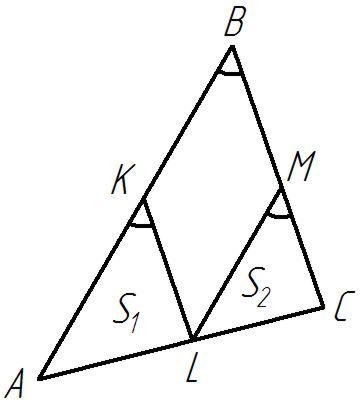
Рисунок 15
Решение:
Пусть 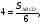
1) 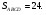
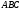
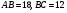
2) 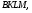
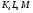
3) 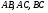
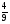
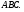
4) 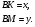 подобен
подобен 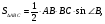 по двум углам.
по двум углам.
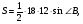 как накрест лежащие,
как накрест лежащие,
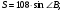
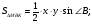 соответственные углы.
соответственные углы.
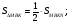
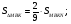
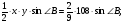
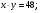
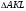 .
.
Составляем систему:
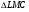
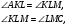 или
или 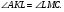
Ответ: 12 и 4 или 6 и 8.
Другой способ решения данной задачи:
1) 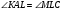
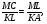
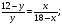
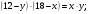
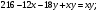
Пусть 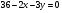
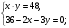
2) 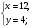
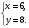
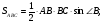
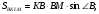
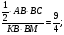
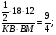
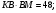
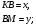
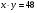
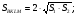
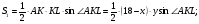
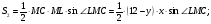
Ответ: 6 и 8 или 12 и 4.
Задача 2. В треугольнике 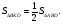 на прямой
на прямой 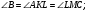 выбрана точка
выбрана точка 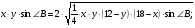 так, что
так, что 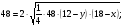 Точка
Точка 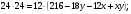 середина стороны
середина стороны 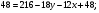 Прямая
Прямая 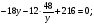 пересекает отрезок
пересекает отрезок 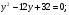 в точке
в точке 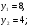 Найдите площадь треугольника
Найдите площадь треугольника 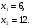 если площадь треугольника
если площадь треугольника 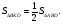 равна 120.
равна 120.
1 случай.
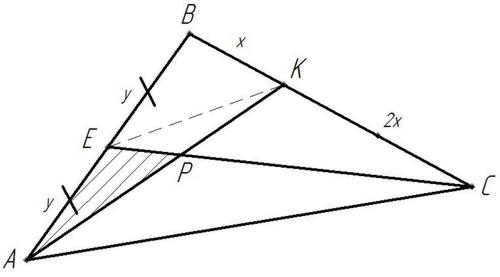
Рисунок 16
Решение:
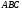
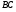 (
(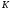 медиана).
медиана).
Пусть 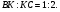
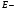
1) 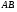
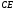
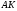
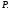
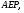
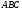
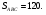
2) 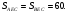 и
и 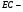
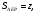
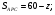
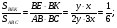
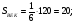
Ответ: 12.
2 случай.
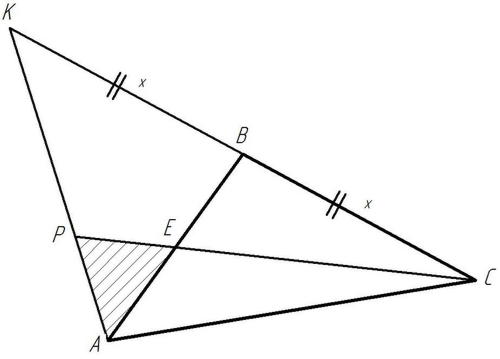
Рисунок 17
Решение:
1) 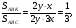
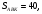 медиана,
медиана,
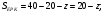
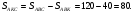 медиана;
медиана;
Пусть 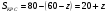 ,
,
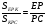
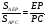
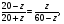 медиана,
медиана,
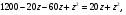
2) 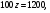 общая высота,
общая высота, 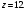 общая высота.
общая высота.
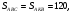
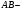
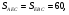
Ответ: 20.
Задача 3. Через точку 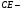 лежащую в треугольнике
лежащую в треугольнике 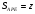 проведены три прямые, параллельные всем сторонам треугольника. В результате треугольник разбился на 3 треугольника и 3 параллелограмма. Известно, что площади полученных треугольников равны соответственно 1;2,25и 4. Найдите сумму площадей полученных параллелограммов.
проведены три прямые, параллельные всем сторонам треугольника. В результате треугольник разбился на 3 треугольника и 3 параллелограмма. Известно, что площади полученных треугольников равны соответственно 1;2,25и 4. Найдите сумму площадей полученных параллелограммов.
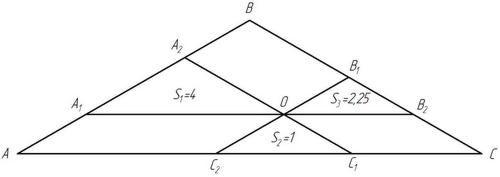
Рисунок 18
Найти: 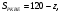
Решение:
1) Рассмотрим 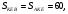
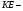
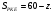
2) Рассмотрим 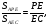
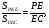
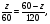
3) Рассмотрим 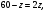
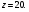
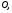
4) 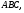
Ответ: 13.
Задача 4. Площадь трапеции 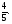 равна 810. Диагонали пересекаются в точке
равна 810. Диагонали пересекаются в точке 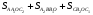
Отрезки, соединяющие середину 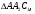 основания
основания 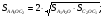 с вершинами
с вершинами 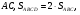 и
и 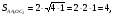 пересекаются с диагоналями трапеции в точках
пересекаются с диагоналями трапеции в точках 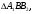 и
и 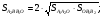 Найдите площадь треугольника
Найдите площадь треугольника 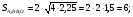 если одно из оснований трапеции вдвое больше другого.
если одно из оснований трапеции вдвое больше другого.
1 случай.
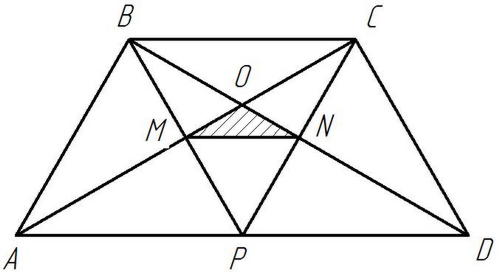
Рисунок 19
Решение:
1) Рассмотрим четырёхугольник 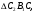
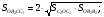 основания трапеции.
основания трапеции. 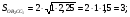 параллелограмм.
параллелограмм.
2) 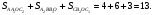 по двум сторонам и углу между ними. Аналогично,
по двум сторонам и углу между ними. Аналогично, Значит,
Значит, 
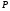
3) 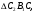 диагонали параллелограмма делят его на четыре равных по площади треугольника.
диагонали параллелограмма делят его на четыре равных по площади треугольника.
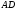
4) Т. к. 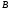 то
то 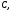 средняя линия треугольника
средняя линия треугольника 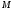
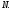
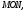
5) 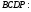 трапеция,
трапеция, 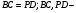
Пусть 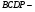 тогда
тогда 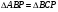
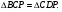
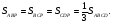
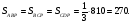
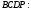
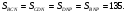
Ответ: 22,5.
2 случай.
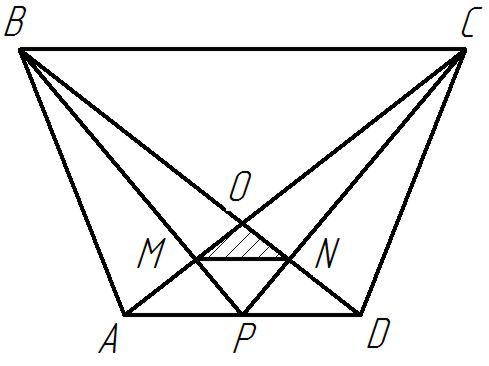
Рисунок 20
Решение:
Пусть 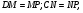 высота трапеции.
высота трапеции.
Положим 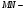 Тогда
Тогда 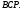
Треугольник 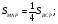 подобен треугольнику
подобен треугольнику 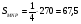 с коэффициентом
с коэффициентом 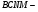 а треугольник
а треугольник 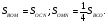 подобен треугольнику
подобен треугольнику 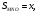 с коэффициентом
с коэффициентом 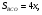 Тогда
Тогда 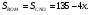
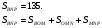
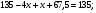
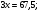
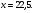
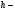 Значит,
Значит, 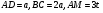 Аналогично,
Аналогично, 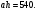
Следовательно, 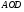
Ответ: 14,4.
Литература:
1. Геометрия. 10 - 11 классы: учеб. для общеобразоват. учреждений: базовый и профил. уровни / [Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др.]. - 22-е изд. - М.: Просвещение, 2013. - 255с.
2. Геометрия в таблицах. 7 - 11 кл.: Справочное пособие / Авт.-сост. Л.И. Звавич, А.Р. Рязановский. - 4-е изд., стереотип. - М.: Дрофа, 2000. - 128 с.
3. http://www.fipi.ru (Официальный сайт Федерального института педагогических измерений)