- Учителю
- Дидактический материал по алгебре за 9 класс
Дидактический материал по алгебре за 9 класс
Школа-лицей №3
Дидактический материал по
алгебре 9 класс.
Учитель: Чеснокова С. А.
Г. Кызылорда
Аннотация
дидактического материала по алгебре
за 9 класс.
Дидактические карточки по курсу алгебры для 9 классов предназначены для организации самостоятельной работы учащихся и для осуществления контроля за их знаниями, умениями и навыками.
Задания карточек рассчитаны на 15-20 минут. Каждая из них может использоваться отдельными фрагментами на различных этапах формирования конкретных умений.
С помощью карточек можно дифференцировать деятельность учащихся согласно содержанию материала, выделяя для разных учеников разные фрагменты карточки.
Цели дидактического материала:
-
Индивидуальная деятельность учащихся.
-
Развитие мыслительной деятельности учащихся.
-
Воспитание самостоятельности при выполнении заданий карточек.
-
Накопляемость оценок.
Используемая литература:
-
Приложение к журналу « 1 сентября - математика»
-
Учебник « Алгебра - 9» - автор Ю.Н. Макарычев, Н.г. Миндюк, К.И. М Нешков.
-
«Дидактические материалы по алгебре» С.В.Кудрявцев, Ю.Н.Макарычев.
-
Учебник « Алгебра - 9» автор Н.Я.Виленкин
-
«Дидактические материалы по алгебре»
 А.Н.Шыныбеков
А.Н.Шыныбеков
Календарный план по алгебре за 9 класс.
2 часа в неделю, всего 68 часов.
№ урока
Тема урока.
Кол-во часов
Сроки
1-3
1-я четверть.
Повторение. Квадратные корни, квадратное уравнение, системы уравнений.
3
4
Контрольная работа № 1 по итогам повторения.
1
5,6
Глава 1. Уравнения с двумя переменными, неравенства и их системы.
Уравнения с двумя переменными и их геометрический смысл.
9
2
7,8
Решение систем уравнений с двумя переменными.
2
9,10
Задачи, решаемые составлением систем уравнений.
2
11,12
Решение систем неравенств с одной переменной.
2
13
Контрольная работа № 2 .
1
14
Глава 2. Элементы тригонометрии.
Углы и дуги. Радианная мера угла.
18
1
15,16
Определение тригонометрических функций.
2
17
Свойства тригонометрических функций.
1
18
Контрольная работа № 3 за 1-ю четверть.
1
19
2-я четверть.
Свойства тригонометрических функций.
1
20,21
Формулы приведения
2
22,23
Преобразование тригонометрических выражений.
2
24
Контрольная работа № 4.
1
25,26
Формулы суммы.
2
27,28
Формулы двойного и половинного углов.
2
29,30
Формулы преобразования суммы и разности тригонометрических функций в произведение и из произведения в сумму.
2
31,32
Контрольная работа № 5 за 1-е полугодие
2
33,34
3-я четверть
Глава 3. Прогрессии.
Арифметическая прогрессия.
Определение арифметической прогрессии. Формула общего члена.
10
2
35,36
Формула п-первых членов арифметической прогрессии.
2
37
Контрольная работа № 6.
1
38
Геометрическая прогрессия.
Определение геометрической прогрессии. Формула общего члена.
1
39,40
Сумма п-первых членов геометрической прогрессии.
2
41
Бесконечно убывающая геометрическая прогрессия.
1
42
Контрольная работа № 7
1
43,44
Глава 4. Степенная, показательная, логарифмическая функции.
Степенная функция с целым показателем.
23
2
45,46
Корень п-ой степени и его свойства.
2
47,48
Степень с рациональным показателем и её свойства. Понятие степени с иррациональным показателем.
2
49
Преобразование выражений со степенью и со знаком корня.
1
50,51
Показательная функция и её свойства.
2
52,53
Контрольная работа № 8 за 3-ю четверть.
2
54-56
4-я четверть.
Логарифм числа и его свойства.
3
57-59
Логарифмическая функция её свойства и график.
3
60
Число е. Показательная и логарифмическая функция с основанием, равным е.
1
61-63
Показательные и логарифмические уравнения и их системы.
3
64,65
Решение показательных и логарифмических неравенств.
2
66-68
Повторение, итоговая контрольная работа № 9.
3
Учитель: Чеснокова С.А.
Каталог дидактических карточек по алгебре
9 класс.
-
Повторение материала за курс алгебры 8 класс.
-
Уравнения с двумя переменными и их геометрический смысл.
-
Решение систем уравнений второй степени.
-
Задачи решаемые составлением систем уравнений.
-
Решение систем неравенств с одной переменной.
-
Определение тригонометрических функций.
-
Свойства тригонометрических функций.
-
Формулы приведения.
-
Преобразование тригонометрических выражений.
-
Формулы суммы.
-
Формулы двойного и половинного углов.
-
Формулы преобразования суммы и разности тригонометрических функций в произведение и из произведения в сумму.
-
Формула п-первых членов арифметической прогрессии
-
Формула п-первых членов геометрической прогрессии.
-
Бесконечно убывающая геометрическая прогрессия.
-
Степенная функция с целым показателем.
-
Корень п-ой степени и его свойства.
-
Степень с рациональным показателем и её свойства.
-
Преобразование выражений со степенью и со знаком корня.
-
Показательная функция и её свойства.
-
Логарифм числа и его свойства.
-
Логарифмическая функция и её график.
-
Показательные и логарифмические уравнения и их системы.
-
Решение показательных и логарифмических неравенств.
Тема № 1: «Повторение материала за курс алгебры 8 кл.».
1. Вычислите:
![]()
![]()

Тема № 1: «Повторение материала за курс алгебры 8 кл.».
-
Решите неравенство:
![]()
-
Решите систему уравнений:
![]()
![]()
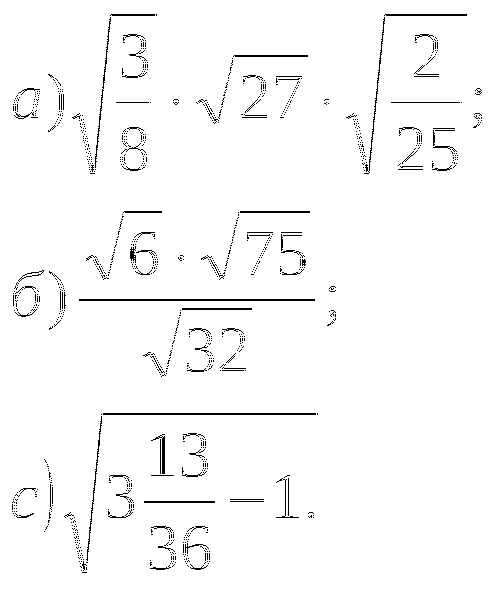
Тема № 1: «Повторение материала за курс алгебры 8 кл.».
1. Приведите уравнение к виду ![]() и решите его:
и решите его:

Тема № 1: «Повторение материала за курс алгебры 8 кл.».
1. Приведите уравнение к виду ![]() и решите его:
и решите его:

Тема № 1: «Повторение материала за курс алгебры 8 кл.».
1. Найдите множество корней уравнения:
![]()
![]()
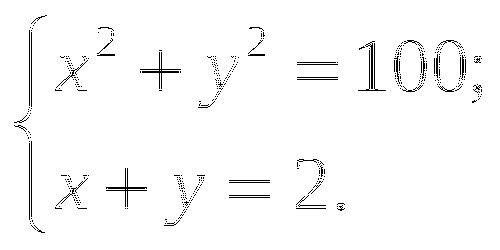
Тема № 1: «Повторение материала за курс алгебры 8 кл.».
1. Найдите множество корней уравнения:
![]()
![]()
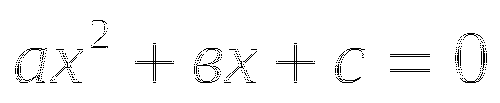
Тема № 2: «Уравнения с двумя переменными и их геометрический смысл».
-
Определите степень уравнения:
а) ![]()
b) ![]()
2. Напишите уравнение окружности с центром в точке ![]() и радиусом
и радиусом ![]() .
.
Тема № 2: «Уравнения с двумя переменными и их геометрический смысл».
1. Прямая задана уравнением ![]() . Найдите:
. Найдите:
а) угловой коэффициент; б) ординату точки этой прямой, абсцисса которой равна а. Постройте график этого уравнения.
2. Принадлежит ли точка А(1; а) графику уравнения:
![]()
Тема № 2: «Уравнения с двумя переменными и их геометрический смысл».
-
Окружность задана уравнением
 Найдите: а) Координаты центра; b) радиус. Постройте ее график.
Найдите: а) Координаты центра; b) радиус. Постройте ее график. -
Парабола задана уравнением
 Найдите : а) координаты ее вершины; b) точки пересечения с осями координат. Постройте ее график.
Найдите : а) координаты ее вершины; b) точки пересечения с осями координат. Постройте ее график.
Тема № 2: «Уравнения с двумя переменными и их геометрический смысл».
![]()
![]()
-
Определите угловой коэффициент прямой:
![]()
2. Принадлежит ли точка А( -b; с) графику уравнения:
а) ![]()
б) ![]()
Тема № 3: «Решение систем уравнений второй степени».
-
Решите систему уравнений:
а) 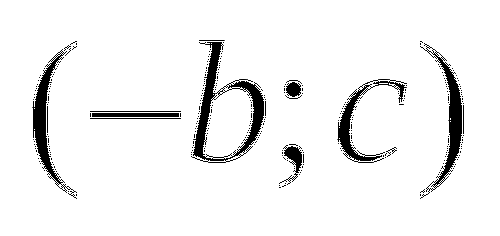
б) 
Тема № 3: «Решение систем уравнений второй степени».
-
Решите систему уравнений:
а) 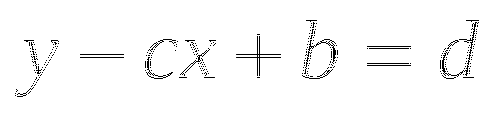
б) 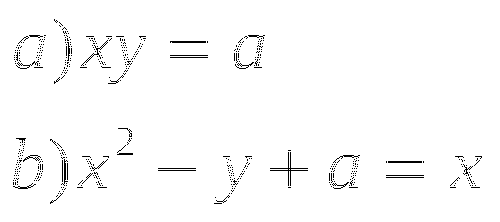
Тема № 3: «Решение систем уравнений второй степени».
-
Решите систему уравнений:
а) 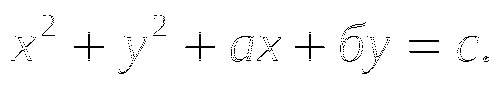
б) 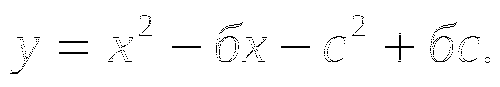
Тема № 3: «Решение систем уравнений второй степени».
-
Решите систему уравнений:
а) 
б) 
Тема № 3: «Решение систем уравнений второй степени».
-
Решите систему уравнений:
а) 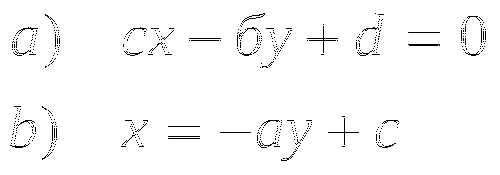
б) 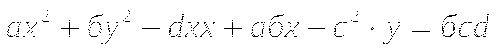
Тема № 3: «Решение систем уравнений второй степени».
-
Решите систему уравнений:
а) 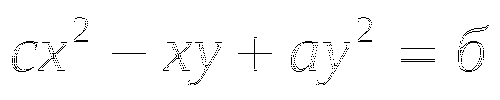
б) 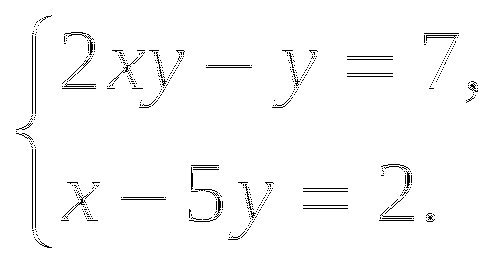
Тема № 4: «Задачи, решаемые составлением систем уравнений»
1. Диагональ прямоугольника равна 10 см, а его периметр равен 28 см. Найдите стороны прямоугольника.
Тема № 4: «Задачи, решаемые составлением систем уравнений»
1. Прямоугольный участок земли, площадью 2400 м2 обнесён изгородью, длина которой 200 м. Найдите длину и ширину этого участка.
Тема № 4: «Задачи, решаемые составлением систем уравнений»
1. Из некоторого пункта вышли одновременно два отряда. Один направился на север, а другой на восток. Спустя 4 ч. расстояние между отрядами было равно 24 км, причём первый отряд прошёл на 4,8 км больше, чем второй. С какой скоростью шёл каждый отряд?
Тема № 4: «Задачи, решаемые составлением систем уравнений»
1. На каждой из сторон прямоугольника построен квадрат. Сумма площадей квадратов равна 122 см2.Найдите стороны прямоугольника если известно, что его площадь равна 30 см2.
Тема № 4: «Задачи, решаемые составлением систем уравнений»
1. Двузначное число в два раза больше суммы своих цифр и в два раза больше произведения этих цифр. Найдите данное двузначное число.
Тема № 4: «Задачи, решаемые составлением систем уравнений»
1. Если возвести в квадрат числитель дроби, а знаменатель увеличить на 7, то получим число равное 0,75. Если числитель данной дроби оставить без изменения, а знаменатель увеличить на 1, то получим число, равное 0,5. Найдите заданное дробное число.
Тема № 5: «Решение систем неравенств с одной переменной».
1. Решите неравенство:
а) ![]()
б) ![]()
в) ![]()
Тема № 5: «Решение систем неравенств с одной переменной».
-
Решите неравенство:
а) ![]()
б) ![]()
в) ![]()
Тема № 5: «Решение систем неравенств с одной переменной».
-
Найдите множество решений неравенства:
а) ![]()
б) ![]()
Тема № 5: «Решение систем неравенств с одной переменной».
-
Найдите множество решений неравенства:
а) ![]()
б) ![]()
Тема № 5: «Решение систем неравенств с одной переменной».
-
Решите неравенство:
а) ![]()
б) ![]()
в) ![]()
Тема № 5: «Решение систем неравенств с одной переменной».
-
Решите неравенство:
а) ![]()
б) ![]()
в) ![]()
![]()
![]() Тема № 6: «Определение тригонометрических функций».
Тема № 6: «Определение тригонометрических функций».
-
Найдите значение выражения:
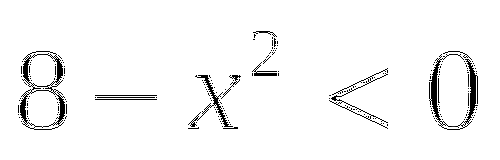
![]() Тема № 6: «Определение тригонометрических функций».
Тема № 6: «Определение тригонометрических функций».
1.![]() Найдите значение выражения:
Найдите значение выражения:
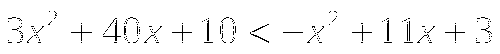
Тема № 6: «Определение тригонометрических функций».
-
Найдите значение выражения:
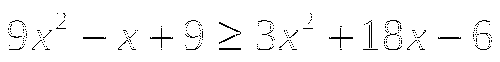
Тема № 6: «Определение тригонометрических функций».
-
Вычислите:
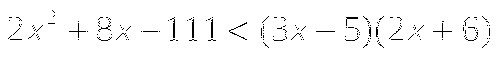
![]()
![]()
Тема № 6: «Определение тригонометрических функций».
-
Найдите значение выражения
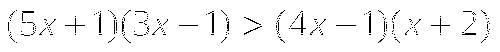 если:
если:
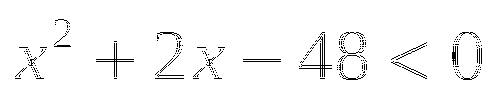
Тема № 6: «Определение тригонометрических функций».
-
Найдите значение выражения:
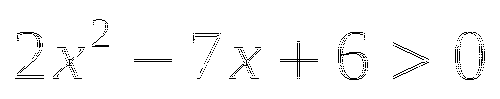
![]()
![]()
Тема № 7: «Свойства тригонометрических функций».
-
Какой знак имеет:
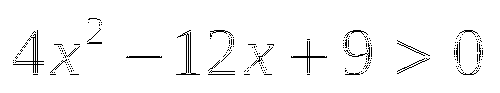
Тема № 7: «Свойства тригонометрических функций».
1. Какой знак имеет:
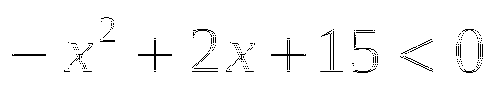
Тема № 7: «Свойства тригонометрических функций».
-
Углом какой четверти является угол a, если:
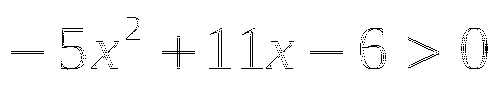
Тема № 7: «Свойства тригонометрических функций».
-
Углом какой четверти является угол a, если:
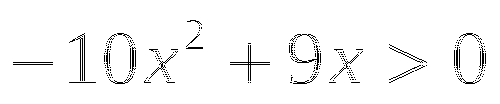
Тема № 7: «Свойства тригонометрических функций».
-
Определите знак выражения:

Тема № 7: «Свойства тригонометрических функций».
-
Найдите

Тема № 8: «Формулы приведения».
-
Замените тригонометрической функцией угла а:
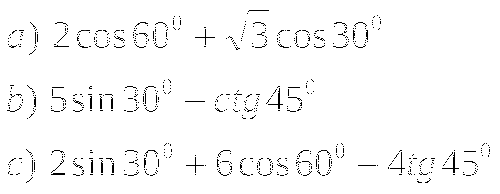
Тема № 8: «Формулы приведения».
-
Замените тригонометрической функцией угла а:

Тема № 8: «Формулы приведения».
-
Найдите значение выражения:

Тема № 8: «Формулы приведения».
1. Найдите:
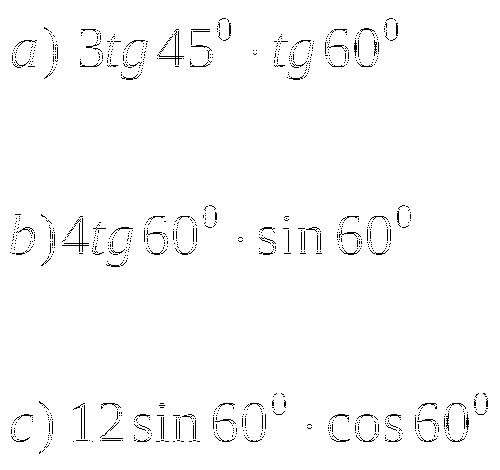
Тема № 8: «Формулы приведения».
-
Упростите выражение:
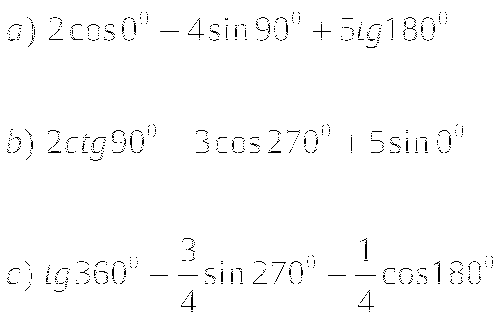
Тема № 8: «Формулы приведения».
-
Упростите выражение:
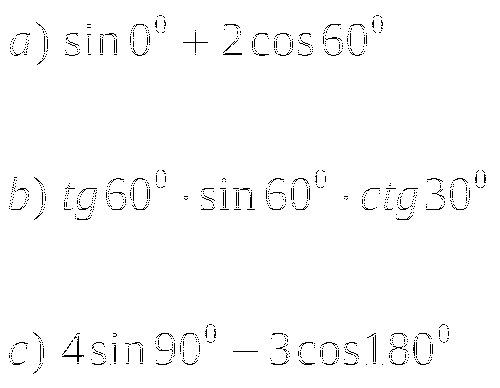
Тема № 8: «Формулы приведения».
-
Преобразуйте выражение:

Тема № 9: «Преобразование тригонометрических выражений».
-
Преобразуйте выражение:

Тема № 9: «Преобразование тригонометрических выражений».
-
Докажите, что при всех допустимых значениях
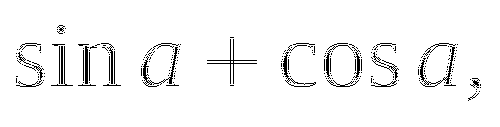 значение выражения не зависит от
значение выражения не зависит от 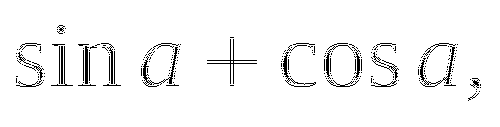 :
:
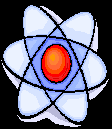
Тема № 9: «Преобразование тригонометрических выражений».
-
Докажите, что при всех допустимых значениях a выражение принимает одно и то же значение:
Тема № 9: «Преобразование тригонометрических выражений».
-
Упростите выражение:

Тема № 9: «Преобразование тригонометрических выражений».
-
Упростите выражение:

Тема № 9: «Преобразование тригонометрических выражений».
-
Упростите выражение:
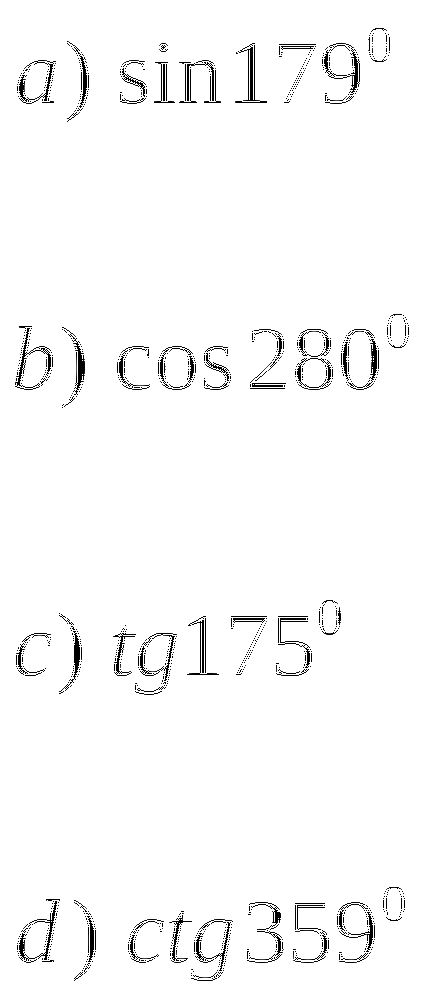
Тема № 10: «Формулы суммы».
-
С помощью формул сложения преобразуйте выражение:
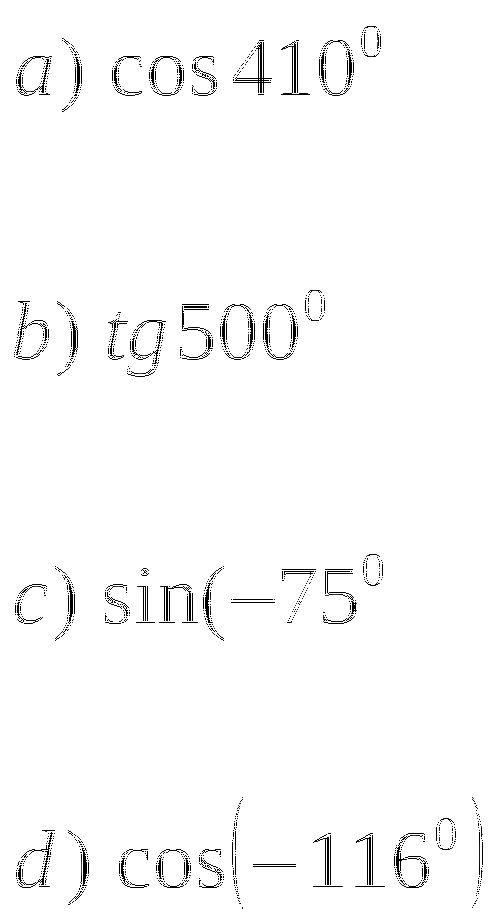
Тема № 10: «Формулы суммы».
-
С помощью формул сложения преобразуйте выражение:
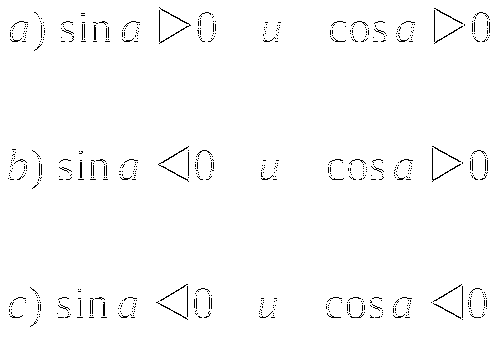
Тема № 10: «Формулы суммы».
-
Представив
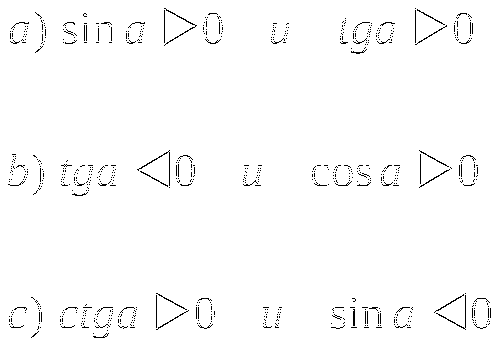 как сумму
как сумму 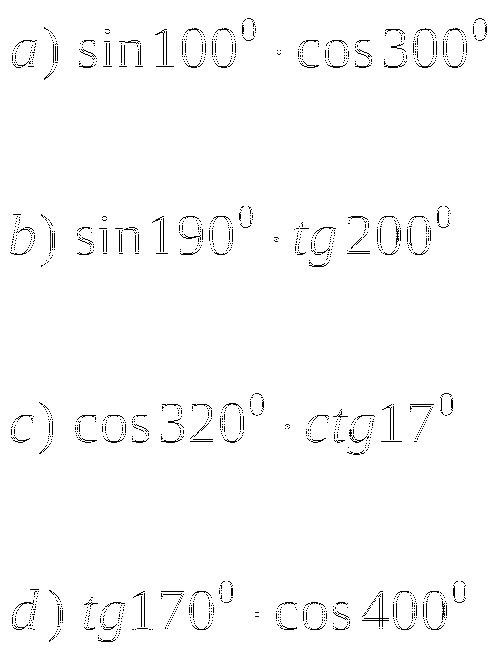 , вычислите:
, вычислите:
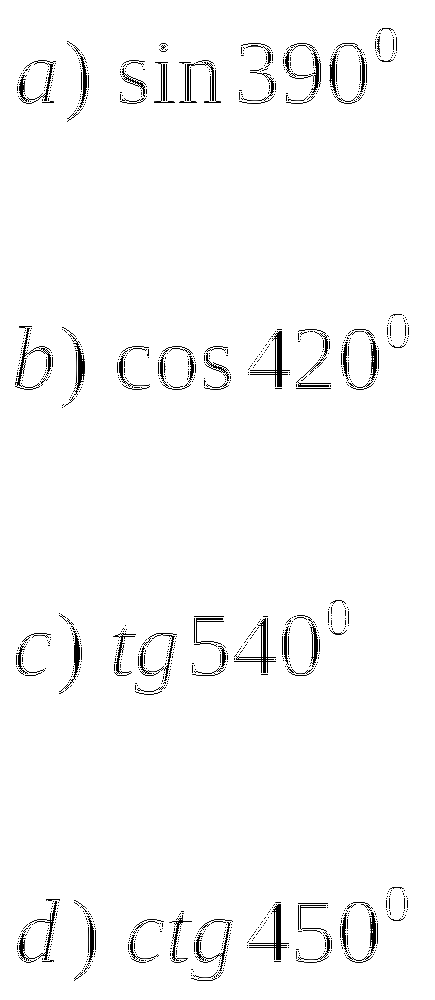
Тема № 10: «Формулы суммы».
-
Упростите выражение:
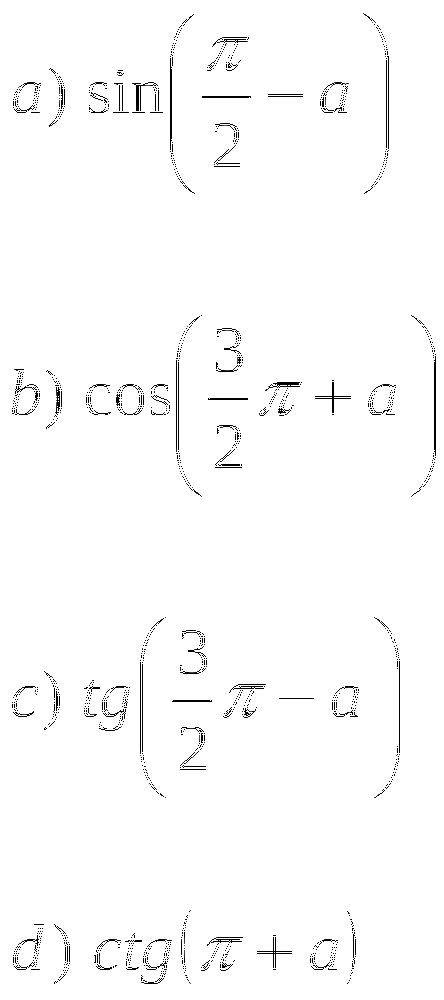
Тема № 10: «Формулы суммы».
-
Упростите выражение:
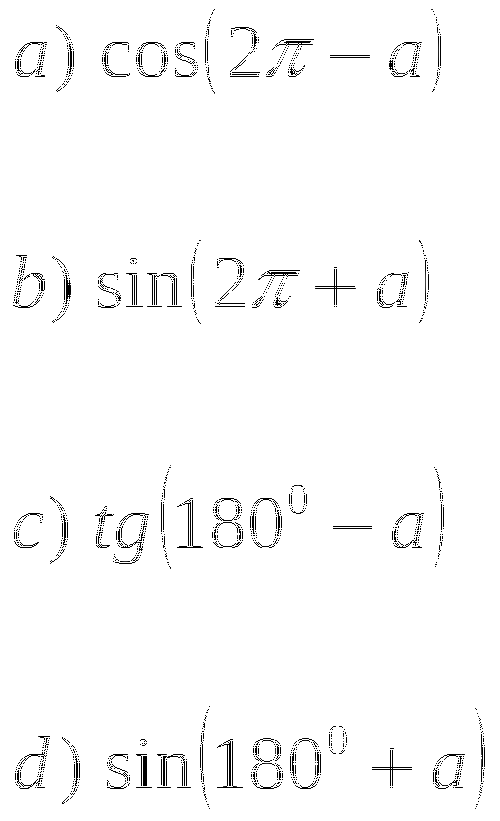
Тема № 10: «Формулы суммы».
-
Упростите выражение:
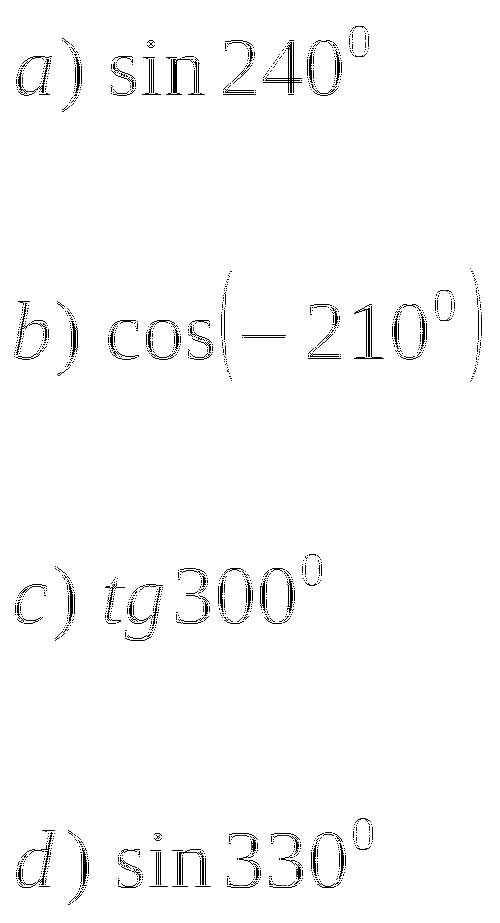
Тема № 10: «Формулы суммы».
-
Найдите значение выражения:
![]()
![]()
![]()
Тема № 10: «Формулы суммы».
-
Упростите:
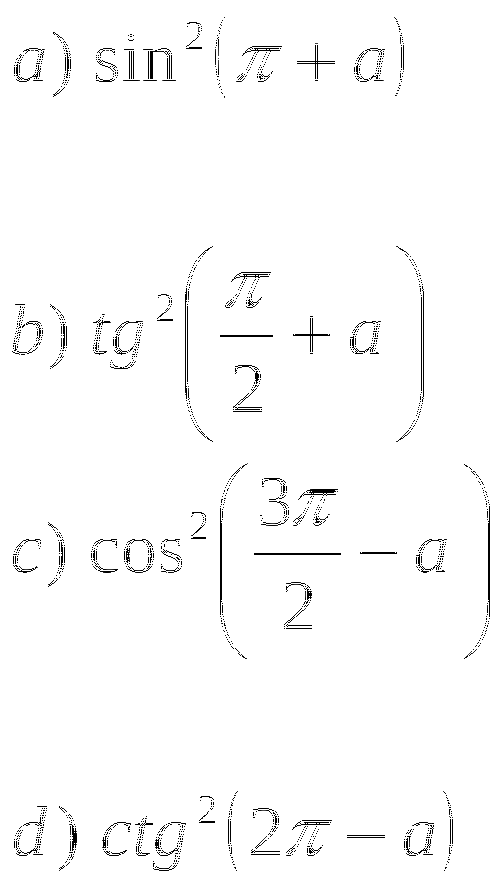
Тема № 11: «Формулы двойного и половинного углов».
1. Упростите выражение:
![]()
![]()
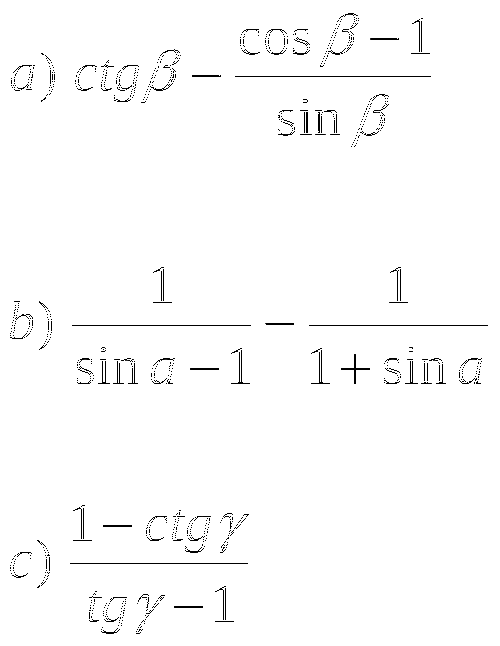
Тема № 11: «Формулы двойного и половинного углов».
1. Упростите выражение:
![]()
![]()

Тема № 11: «Формулы двойного и половинного углов».
1. Упростите выражение:
![]()
![]()

Тема № 11: «Формулы двойного и половинного углов».
1. Упростите выражение:
![]()
![]()
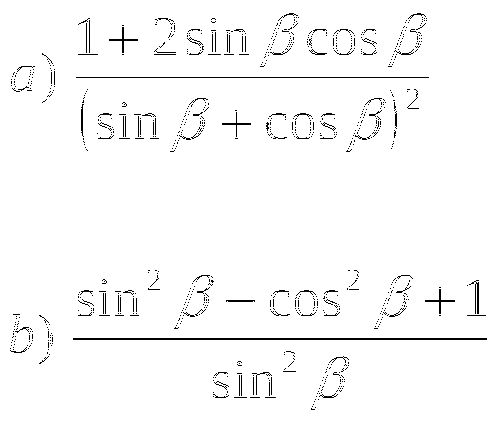
Тема № 11: «Формулы двойного и половинного углов».
1. Вычислите:
![]()
![]()
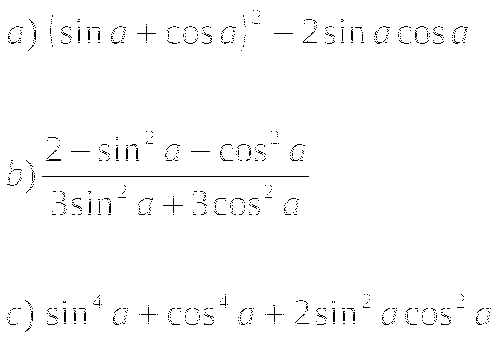
Тема № 11: «Формулы двойного и половинного углов».
1. Вычислите:
![]()
![]()
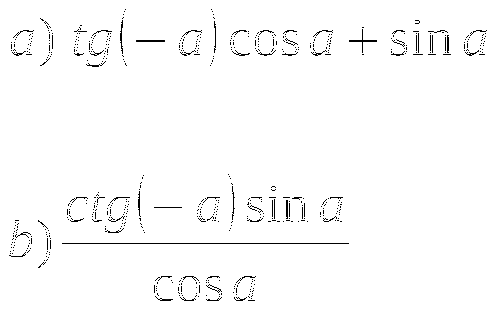
![]()
![]()
Тема № 11: «Формулы двойного и половинного углов».
1. Вычислите:
![]()
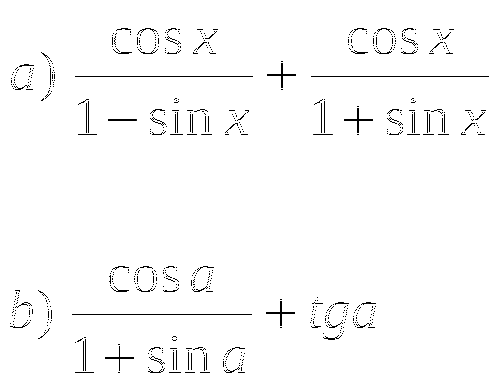
Тема № 11: «Формулы двойного и половинного углов».
1. Вычислите:
![]()
![]()
![]()
Тема № 11: «Формулы двойного и половинного углов».
1. Вычислите:
![]()
![]()
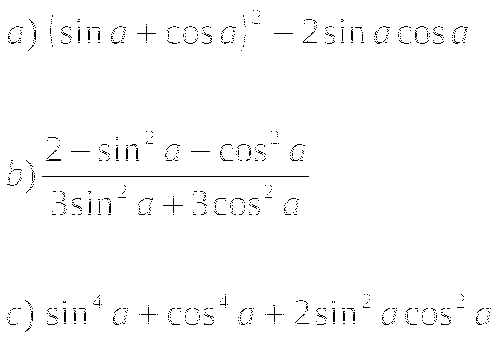
Тема № 11: «Формулы двойного и половинного углов».
![]()
![]() 1. Вычислите:
1. Вычислите:
![]()
![]()
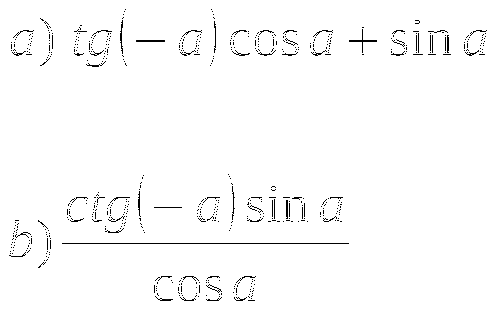
Тема № 11: «Формулы двойного и половинного углов».
1. Вычислите:
![]()
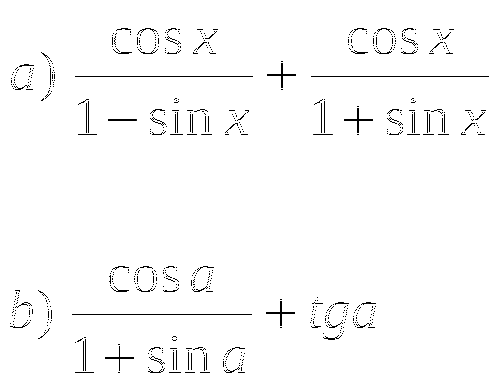
Тема № 11: «Формулы двойного и половинного углов».
1. Вычислите:
![]()
![]()
![]()
Тема № 12: «Формулы преобразования суммы и разности тригонометрических функций в произведение и из произведения в сумму».
-
Представьте в виде произведения:
а) ![]()
б) ![]()
в) ![]()
г) ![]()
Тема № 12: «Формулы преобразования суммы и разности тригонометрических функций в произведение и из произведения в сумму».
-
Разложите на множители выражение:
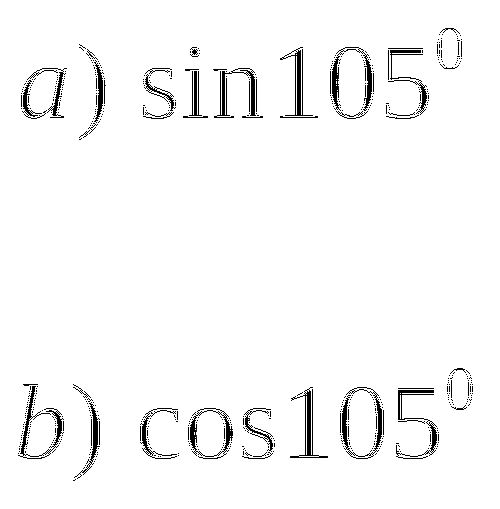
Тема № 12: «Формулы преобразования суммы и разности тригонометрических функций в произведение и из произведения в сумму».
-
Представьте в виде произведения:
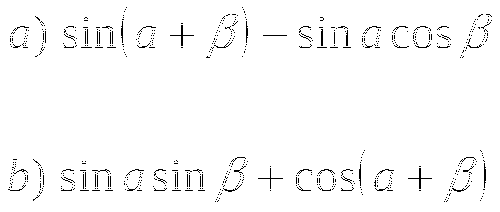
Тема № 12: «Формулы преобразования суммы и разности тригонометрических функций в произведение и из произведения в сумму».
-
Представьте в виде произведения выражение:
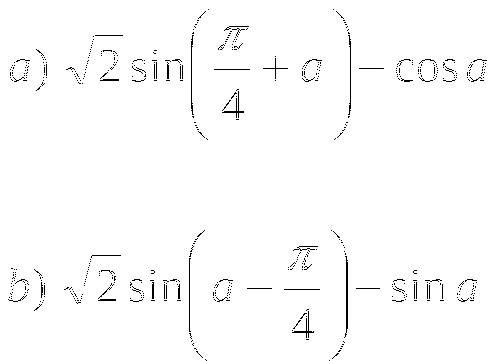
Тема № 12: «Формулы преобразования суммы и разности тригонометрических функций в произведение и из произведения в сумму».
-
Докажите что:
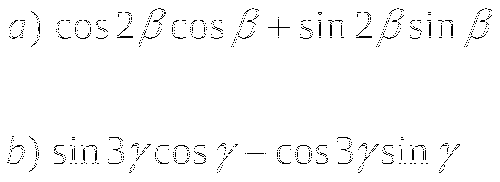
Тема № 12: «Формулы преобразования суммы и разности тригонометрических функций в произведение и из произведения в сумму».
-
Представьте в виде произведения тригонометрических функций:

Тема № 12: «Формулы преобразования суммы и разности тригонометрических функций в произведение и из произведения в сумму».
-
Представьте в виде произведения:
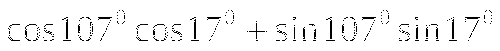
Тема № 13: «Формула n- первых членов арифметической прогрессии».
-
Выпишите первые пять членов арифметической
прогрессии (ап), если:
![]()
![]()
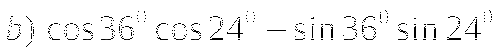
Тема № 13: «Формула n- первых членов арифметической прогрессии».
-
Последовательность (bп)- арифметическая
прогрессия, первый член которой равен =b1,а
разность равна d. Выразите через b1 и d:
![]()
![]()
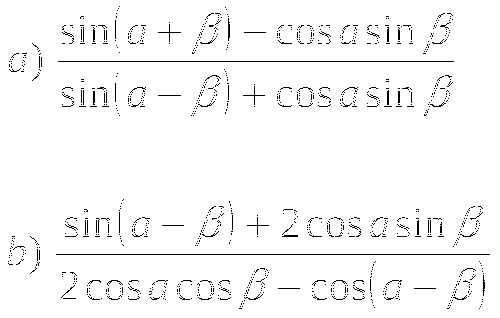
Тема № 13: «Формула n- первых членов арифметической прогрессии».
1. Найдите десятый п-й член арифметической прогрессии:
![]()
![]()

Тема № 13: «Формула n- первых членов арифметической прогрессии».
-
Последовательность (сп)- геометрической прогрессия, первый член которой равен =с1,а разность равна q. Выразите через c1 и q:
![]()
![]()

Тема № 13: «Формула n- первых членов арифметической прогрессии».
-
Найдите первый член и разность арифметической прогрессии (сп), если:
а)с5=27, с27=60;
б)с20=0, с66=-92.
Тема № 13: «Формула n- первых членов арифметической прогрессии».
1. Найдите 23-й и п-й член арифметической прогрессии:
![]()
![]()
![]()
Тема № 13: «Формула n- первых членов арифметической прогрессии».
1.Между числами 5 и 1 вставьте семь таких чисел, чтобы они вмести с данными числами образовали арифметическую прогрессию.
Тема № 13: «Формула n- первых членов арифметической прогрессии».
-
Последовательность (сп)- геометрической прогрессия, первый член которой равен =с1,а разность равна q. Выразите через c1 и q:
![]()
![]()

Тема № 14: «Формула n- первых членов геометрической прогрессии».
-
Найдите первые пять членов геометрической прогрессии (вп), если:
![]()
![]()

Тема № 14: «Формула n- первых членов геометрической прогрессии».
-
Последовательность (сп)- геометрической прогрессия, первый член которой равен =с1,а разность равна q. Выразите через c1 и q:
![]()
![]()

Тема № 14: «Формула n- первых членов геометрической прогрессии».
-
Последовательность (xп)- геометрическая прогрессия. Найдите:
![]()
![]()

Тема № 14: «Формула n- первых членов геометрической прогрессии».
-
Последовательность (bп)- геометрическая прогрессия. Найдите:
![]()
![]()
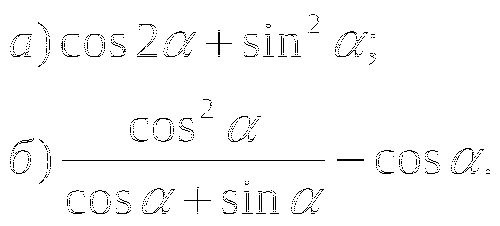
Тема № 14: «Формула п-го члена геометрической прогрессии».
1. Найдите седьмой п-й член геометрической прогрессии:
![]()
![]()
![]()
Тема № 14: «Формула п-го члена геометрической прогрессии».
-
Найдите знаменатель геометрическая прогрессия. Найдите:
![]()
![]()
![]()
Тема № 14: Тема: «Формула п-го члена геометрической прогрессии».
-
Между числами 2 и 162 вставьте такие три числа, которые вместе с данными числами образуют геометрическую прогрессию.
Тема № 14: Тема: «Формула п-го члена геометрической прогрессии».
-
Геометрическая прогрессия (хп) состоит из четырёх членов: 2, х2 ,х3 ,
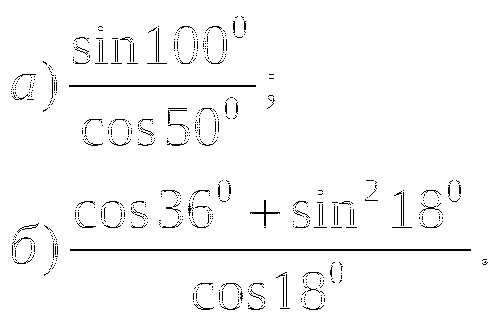 Найдите х2 и х3.
Найдите х2 и х3.
Тема № 14: Тема: «Формула п-го члена геометрической прогрессии».
1. Найдите седьмой п-й член геометрической прогрессии:
![]()
![]()
![]()
Тема № 14: Тема: «Формула п-го члена геометрической прогрессии».
1. Найдите знаменатель геометрическая прогрессия. Найдите:
![]()
![]()
![]()
Тема № 15: Тема: «Бесконечно убывающая геометрическая прогрессия».
1.Проверьте, что знаменатель g данной геометрической прогрессии удовлетворяет условию ![]() , и найдите сумму этой прогрессии:
, и найдите сумму этой прогрессии:

Тема № 15: Тема: «Бесконечно убывающая геометрическая прогрессия».
-
Проверьте, что знаменатель g данной геометрической прогрессии удовлетворяет условию
 , и найдите сумму этой прогрессии:
, и найдите сумму этой прогрессии:
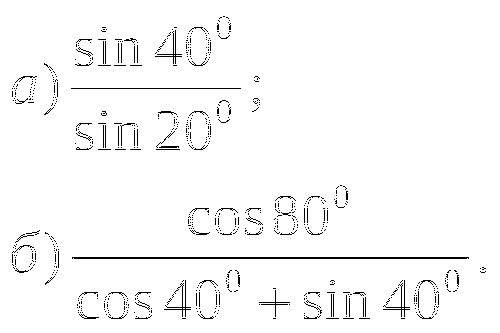
Тема № 15: Тема: «Бесконечно убывающая геометрическая прогрессия».
-
Найдите сумму бесконечной геометрической прогрессии:
![]()
![]()
![]()
Тема № 15: Тема: «Бесконечно убывающая геометрическая прогрессия».
-
Найдите сумму, слагаемые которой являются членами бесконечной геометрической прогрессии


Тема № 16: Тема: «Степенная функция с целым показателем».
1. Функция задана формулой ![]() Сравните:
Сравните:

Тема № 16: Тема: «Степенная функция с целым показателем».
-
Сравните:


Тема № 16: Тема: «Степенная функция с целым показателем».
-
Проходит ли график функции
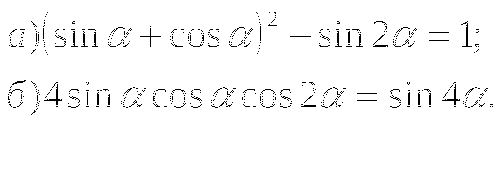 через точку
через точку
А(3; 243), В(-3; 243), С(5; 3125)?
Тема № 16: Тема: «Степенная функция с целым показателем».
-
Принадлежит ли графику функции
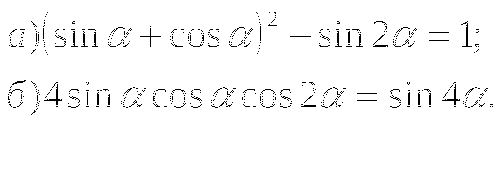 точка:
точка:
А(2; 128), В(-2; -128), С(-3; 2187)?
Тема № 16: Тема: «Степенная функция с целым показателем».
-
Сравните :


Тема № 16: Тема: «Степенная функция с целым показателем».
-
Функция задана формулой
 Сравните:
Сравните:

Тема № 17: Тема: «Корень n- ой степени и его свойства».
-
Найдите значение выражения:

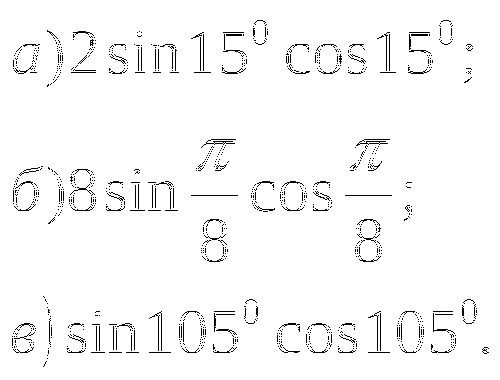
Тема № 17: Тема: «Корень n- ой степени и его свойства».
-
Вычислите:

Тема № 17: Тема: «Корень n- ой степени и его свойства».
-
Принадлежит ли графику функции
 точка:
точка:
Е(81;3); F(81; -3); К(-16; -2); L(0,0001; 0,1) ?
Тема № 17: Тема: «Корень n- ой степени и его свойства».
-
Укажите два последовательных целых числа, между которыми заключено число:

Тема № 17: Тема: «Корень n- ой степени и его свойства».
-
Найдите значение выражения:
а) ![]() б)
б) ![]()
![]()
в) ![]() г)
г) ![]()
д) ![]() е)
е) ![]()
Тема № 17: Тема: «Корень n- ой степени и его свойства».
-
Решите уравнение:
а) ![]() б)
б) ![]()
![]()
в) ![]() г)
г) ![]()
д) ![]() е)
е) ![]()
Тема № 17: Тема: «Корень n- ой степени и его свойства».
-
Найдите значение выражения:
![]() б)
б) ![]()
![]()
в) ![]() г)
г) ![]()
д) ![]() е)
е) ![]()
Тема № 17: Тема: «Корень n- ой степени и его свойства».
![]() 1. Выразите корень п- ой степени из отрицательного числа через арифметический корень той же степени:
1. Выразите корень п- ой степени из отрицательного числа через арифметический корень той же степени:
а) ![]() в)
в) ![]()
б) ![]() г)
г) ![]()
Тема № 18: «Степень с рациональным показателем и её свойства»:
-
Представьте в виде степени с рациональным показателем:
а) ![]() б)
б) ![]()
в) ![]() г)
г) ![]()
д) ![]() e)
e) ![]()
![]()
![]()
Тема № 18: «Степень с рациональным показателем и её свойства»:
-
Представьте в виде степени с рациональным показателем:
а) ![]() б)
б) ![]()
в) ![]() г)
г) ![]()
д) ![]() е)
е) ![]()
Тема № 18: «Степень с рациональным показателем и её свойства»:
-
Упростите выражение:
а) ![]() в)
в) ![]()
б) ![]() г)
г) ![]()
Тема № 18: «Степень с рациональным показателем и её свойства»:
-
Представьте в виде степени:
а) ![]() в)
в) ![]()
б) ![]() г)
г) ![]()
Тема № 18: «Степень с рациональным показателем и её свойства»:
-
Вычислите:
а) ![]() в)
в) ![]()
б) ![]()
![]() г)
г) ![]()
![]()
![]()
![]()
![]()
![]()
![]()
Тема № 18: «Степень с рациональным показателем и её свойства»:
-
Упростите выражение:
а) ![]() в)
в) ![]()
б) ![]()
![]() г)
г) ![]()
![]()
![]()
![]()
![]()
Тема № 19: «Преобразование выражений со степенью и со знаком корня »
-
Упростите выражение:
а)  в)
в) ![]()
б) 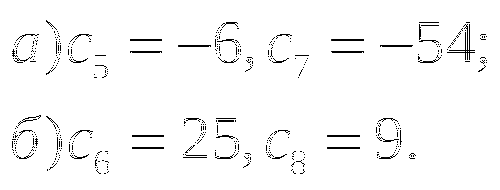 г)
г) 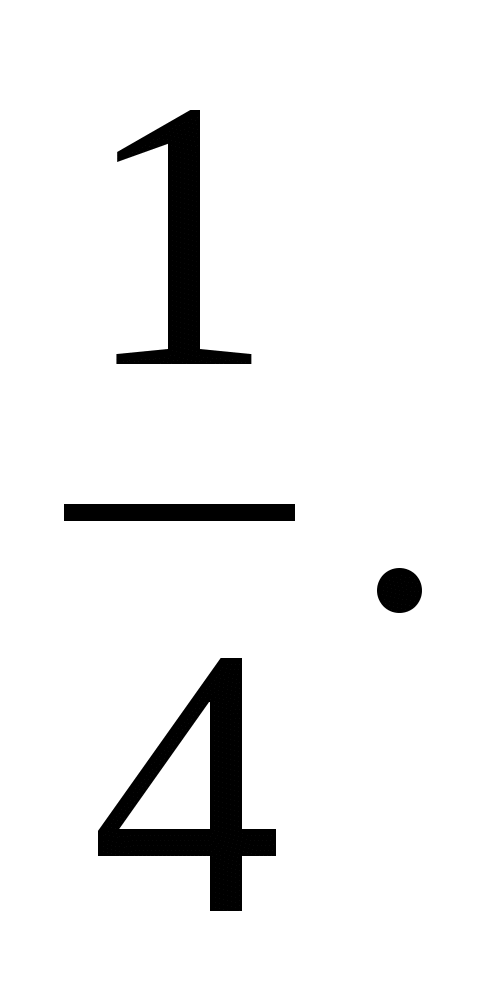
Тема № 19: «Преобразование выражений со степенью и со знаком корня »
-
Вычислите:
а) ![]() б)
б) 
![]()
![]()
Тема № 19: «Преобразование выражений со степенью и со знаком корня »
-
Представьте в виде суммы:
а) ![]() в)
в) ![]()
б) ![]() г)
г) ![]()
Тема № 19: «Преобразование выражений со степенью и со знаком корня »
-
Упростите:
а) 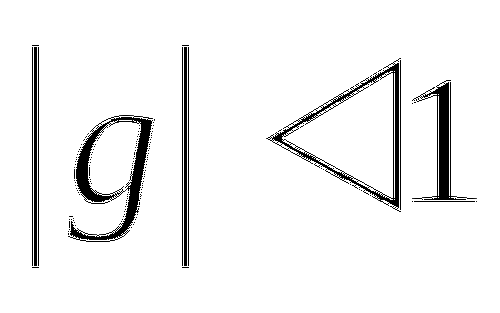 в)
в) ![]()
б)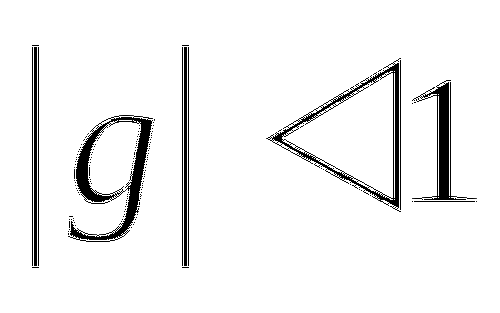 г)
г) ![]()
![]()
Тема № 19: «Преобразование выражений со степенью и со знаком корня »
-
Упростите выражение:
а) ![]() в)
в) ![]()
б) ![]() г)
г) ![]()
Тема № 19: «Преобразование выражений со степенью и со знаком корня »
-
Сократите дробь:
а) 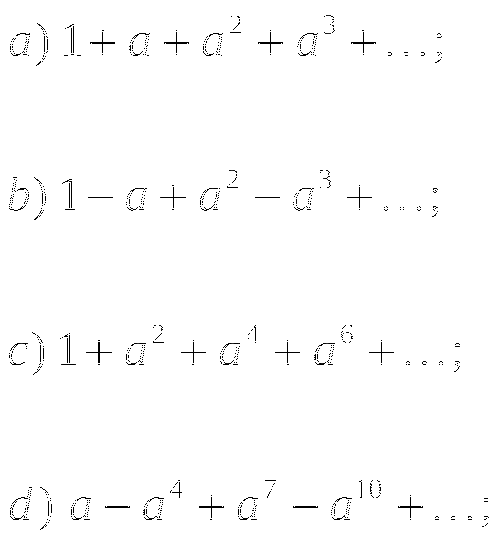 б)
б) 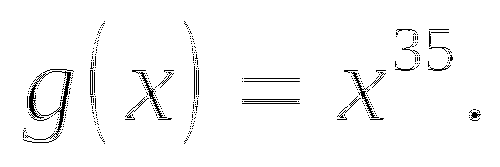
в)  г)
г) 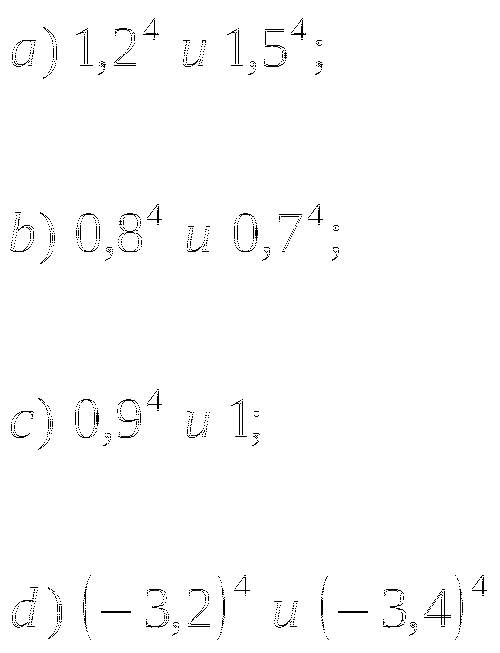
Тема № 19: «Преобразование выражений со степенью и со знаком корня »
![]()
![]()
-
Найдите значение выражения:
а) 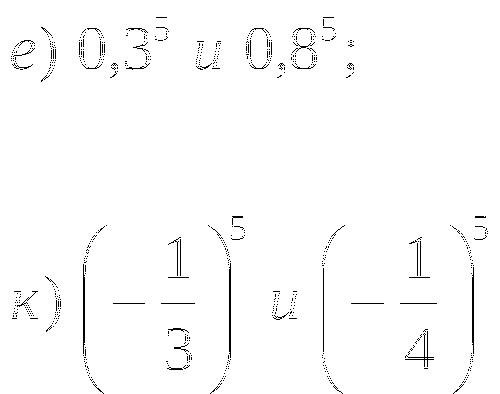 при х=1,44
при х=1,44
б) 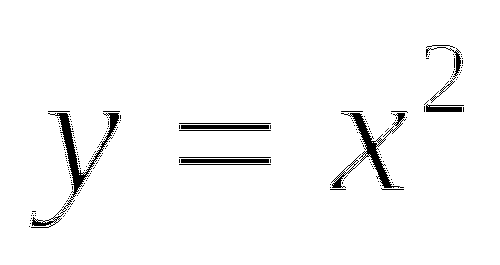 при т=8
при т=8
Тема № 19: «Преобразование выражений со степенью и со знаком корня »
-
Найдите значение выражения:
а) 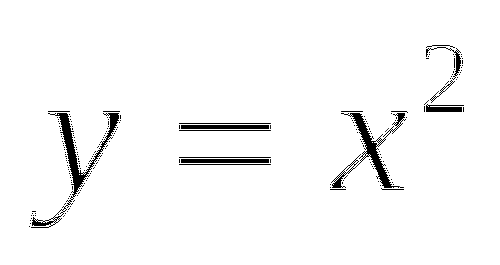
б) 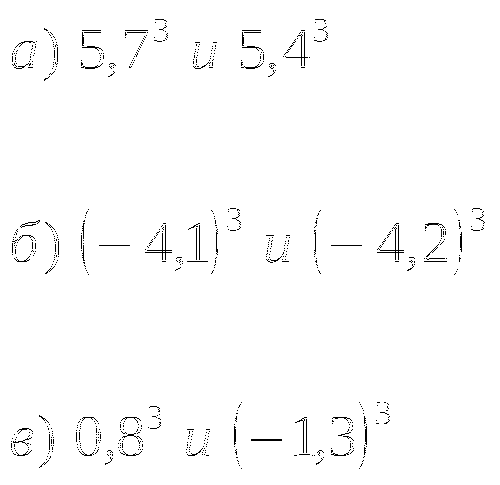
Тема № 20: « Показательная функция и ее свойства»
-
Сравните значение выражений:
а) ![]() в)
в) ![]()
б) ![]() г)
г) ![]()
Тема № 20: « Показательная функция и ее свойства»
1. Сравните значение выражений:
а) ![]() в)
в) ![]()
б) ![]() г)
г) ![]()
![]()
![]()
Тема № 20: « Показательная функция»:
-
Сравните показатели т и п, если известно, что верно неравенство:
а) ![]() в)
в) ![]()
б) ![]() г)
г) ![]()
![]()
![]()
Тема № 20: « Показательная функция»:
-
Сравните показатели т и п, если известно, что верно неравенство:
а) ![]() в)
в) ![]()
б) ![]() г)
г) ![]()
Тема № 20: « Показательная функция»:
-
Решите уравнение:
а) ![]() в)
в) ![]()
б) ![]() г)
г) ![]()
Тема № 20: « Показательная функция»:
-
Решите уравнение:
а) ![]() в)
в) ![]()
б) ![]() г)
г) ![]()
Тема № 21: «Логарифм числа и его свойства»
-
Найдите:
а) ![]() д)
д) ![]()
б) ![]() е)
е) ![]()
в) ![]() ж)
ж) ![]()
г) ![]() з)
з) ![]()
![]()
![]()
Тема № 21: «Логарифм числа и его свойства»
-
Вычислите:
а) ![]()
б) ![]()
в) ![]()
г) ![]()
Тема № 21: «Логарифм числа и его свойства»
-
Вычислите:
а) ![]()
б) ![]()
в) ![]()
г) ![]()
Тема № 21: «Логарифм числа и его свойства»:
-
Вычислите:
а) ![]()
б) ![]()
в) ![]()
г) ![]()
Тема № 21: «Логарифм числа и его свойства»:
-
Вычислите:
а) ![]()
б) ![]()
в) ![]()
г) ![]()
![]()
![]()
Тема № 21: «Логарифм числа и его свойства»:
-
Вычислите:
а) ![]() г)
г) ![]()
б) ![]()
в) ![]()
Тема № 22: «Логарифмическая функция и ее график»:
-
Сравните числа:
а) ![]()
б) ![]()
в) ![]()
г) ![]()
Тема № 22: : «Логарифмическая функция и ее график»:
-
Вычислить, является ли положительным или отрицательным число:
а) ![]()
б) ![]()
в) ![]()
г) ![]()
Тема № 22 : «Логарифмическая функция и ее график»:
-
Выяснить является ли возрастающей или убывающей функция:
а) ![]()
б) ![]()
в) ![]()
г) ![]()
![]()
![]()
Тема № 22: : «Логарифмическая функция и ее график»:
-
Построить график функции
 и по графику найти приближенно
и по графику найти приближенно
а) ![]()
б) ![]()
в) ![]()
г) ![]()
Тема № 23: «Показательные и логарифмические уравнения и их системы»:
1. Решите уравнения:
а) ![]()
б) ![]()
Тема № 23: «Показательные и логарифмические уравнения и их системы»:
-
Решите уравнения:
а) ![]()
б) ![]()
Тема № 23: «Показательные и логарифмические уравнения и их системы»:
![]()
![]() . 1. Решите уравнения:
. 1. Решите уравнения:
а) ![]()
б) ![]()
Тема № 23: «Показательные и логарифмические уравнения и их системы»:
. 1. Решите систему уравнений:
а) 
б) 
Тема № 23: «Показательные и логарифмические уравнения и их системы»:
.
-
Решите систему уравнений:
а) 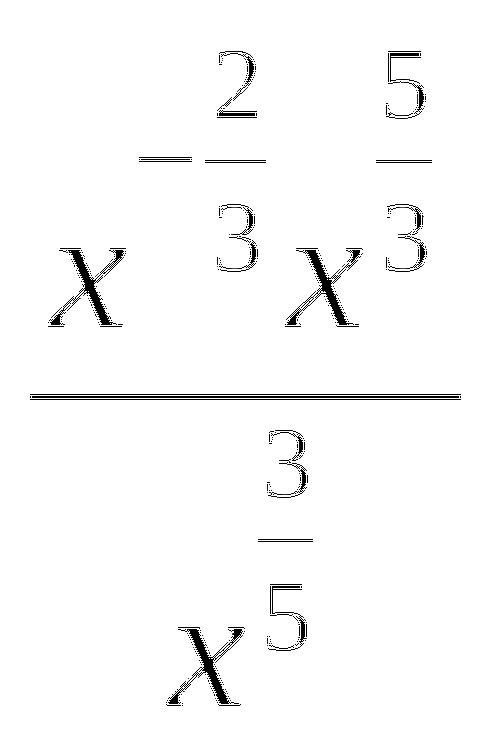
б) 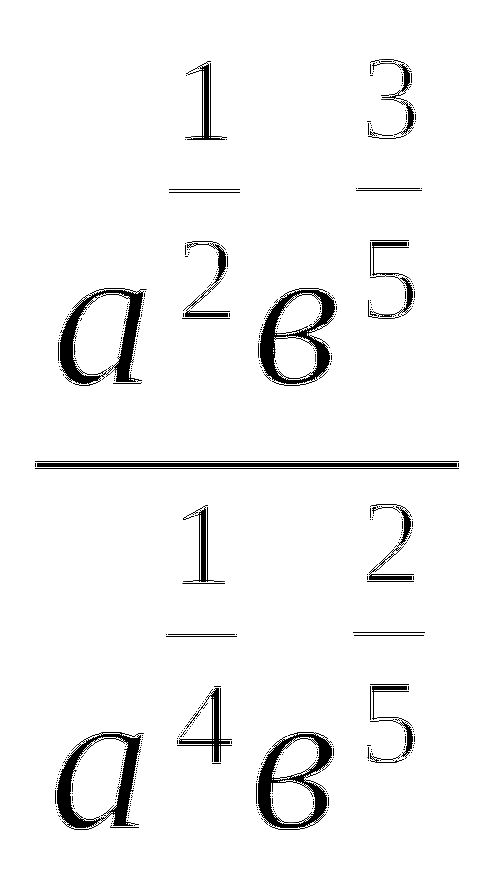
Тема № 23: «Показательные и логарифмические уравнения и их системы»:
![]()
![]() . 1. Решите уравнения:
. 1. Решите уравнения:
а) ![]()
б) ![]()
Тема № 24: «Решение показательных и логарифмических неравенств»:
-
Решите неравенство:
а) ![]()
б) ![]()
![]()
![]()
Тема № 24: «Решение показательных и логарифмических неравенств»:
-
Решите неравенство:
а) ![]()
б) ![]()
Тема № 24: «Решение показательных и логарифмических неравенств»:
-
Решите неравенство:
а) ![]()
б) ![]()
Тема № 24: «Решение показательных и логарифмических неравенств»:
-
Решите неравенство:
а) ![]()
б) ![]()
Тема № 24: «Решение показательных и логарифмических неравенств»:
1,![]()
![]() Решите неравенство:
Решите неравенство:
а)![]()
![]()
б) ![]()
Тема № 24: «Решение показательных и логарифмических неравенств»:
-
Решите неравенство:
а) ![]()
б) ![]()
![]()
![]()
![]()
![]()
![]()
![]()