Урок по математике

Государственное учреждение «Школа-гимназия № 32»

Разработка урока по математике :

Применение тригонометрии к решению задач практического содержания.

Составитель:

учитель высшей категории

Грамлих Галина Владимировна

Астана 2015 год

Тема урока: Применение тригонометрии к решению задач практического содержания.

Цель урока: формирование знаний теоремы косинусов и синусов.

Задачи:

Обучающиеся- определить содержание программных знаний и умений учащихся по данной теме.

Развивающиеся- использование теорем к практическим задачам, активизация познавательной деятельности.

Воспитательные- способность воспитанию чувства удовлетворения и успеха от процесса решения задач.

Форма обучения: фронтальная, индивидуальная.

Тип урока: закрепление.

Оборудование: доска, мультимедийный аппарат.

План урока:

1.Организационный момент.

2.Актуализация опорных знаний.

3.Решение задач.

4.Подведение итогов. Рефлексия.

Ход урока.

1. Постановка цели урока.

2. Актуализация опорных знаний.

Один мудрец сказал: «Высшее проявление духа -это разум. Высшее проявление разума -это геометрия. Клетка геометрии -это треугольник. Он так же неисчерпаем, как и Вселенная».

Изученные нами теоремы косинуса и синуса повторим в виде математического диктанта. Вам необходимо поставить знак «+» или знак «-».

Диктант.

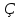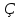1.а²= в²+ с² - ав Соs Sin Sin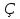

2. Соs (180-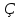) =- Соs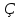

3. =

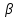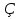
4. с²= а²-в² (для прямоугольного треугольника).

5. Sin (180-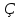) = - Sin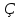

6. =

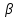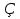
7.в² = а² + с² -2ас Соs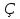

8. 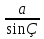=2R

Учащиеся обмениваются листочками ответов, учитель называет правильные ответы. После этого обсуждение ответов со знаком «-».

Записывают тему урока в тетради.

3. Решение задач.

Историческая справка. В 10в. Багдадский ученый Мухаммед из Буджака, известный под именем Аб у-ль - Вефа сформулировал теорему синусов. Насир-эд-Дин из Туса (1201-1274г.) систематически рассмотрел все случаи решения косоугольных треугольников и указал ряд новых способов решения.

Математика морского острова.

Огромный вклад в развитие прикладной геометрии внес трактат китайского ученого ЛЮ Хуэя «Математика морского острова», в котором приведены задачи на определение расстояний до отдельных предметов и вычисление недоступных высот.

Одну из таких задач мы и рассмотрим.

Задача1. Для определения широты непроходимого болота с вертолета, находящегося на высоте 300м измеряют углы 60⁰ и 20⁰. Найти ширину болота.

Франсуа Виет (1540-1603). Виет встал у истоков создания новой науки- тригонометрии. Многие тригонометрические формулы впервые были записаны Виетом.В 1593 году он впервые сформулировал в словесной форме теорему косинусов.

Задача2. Два теплохода начинают движение из одного и того же пункта назначения и двигаются равномерно по прямым пересекающимся под углом 60⁰. Скорость первого 60 км/ч, скорость второго 70 км/ч. Вычислить на каком расстоянии друг от друга они будут находиться через 3 часа.

Задача 3. В 7 часов самолет вылетел из города А в город В. Сделал там получасовую остановку и в 8 ч 30 мин развернул курс на 35⁰ вправо и в 9 часов утра был в городе С. Найти расстояние от А до С, если скорость самолета 300 км/ч

. Задача 4.Самостоятельное решение : 1 вариант 285 а), 2 вариант 285 б).

4 Подведение итогов . Рефлексия.

Сегодня мы с вами убедились, что умение решать треугольники, необходимо каждому человеку в повседневной жизни. Помните, что, решая маленькие задачи вы готовитесь к решению больших и трудных. Андрей Николаевич Колмогоров говорил: «Знания по геометрии умение пользоваться формулами необходимы почти каждому мастеру или рабочему».

Самостоятельное решение задач. 1 вариант 285 а), 2 вариант 285 б).

Домашнее задание № 286, 290

Рефлексия для учителя:

-Активно на уроке работал …

- Старались …

- Жду большей активности от …

Рефлексия для ученика:

-Что больше всего тебе запомнилось на уроке?

-Что удивило?

-Что понравилось всего?

Список литературы

1.С.Е. Чакликова Геометрия 9 класс.

2.Ж. Кайдасов Сборник задач по геометрии 9 класс.