Разработка конспекта урока по алгебре и началам математического анализа на тему 'Применение производной к исследованию функций' (11 класс)

Открытый урок.

«Применение производной для исследования функций»

Цели:

• повторить алгоритм исследования непрерывной функции y=f(x) на монотонность и экстремумы;

• используя общую схему исследования свойств функции и построения ее графика, строить графики функций;

• способствовать развитию вкуса к исследованиям и поискам закономерностей, умению осуществлять наблюдения, формулировать гипотезы.

Планируемый результат урока:

• знать необходимые и достаточные условия экстремума;

• знать схему построения графиков функций;

• уметь по графику производной и изображению знаков производной находить промежутки возрастания и убывания функции, точки экстремумов функций;

• уметь по графику функции определять, сколько решений (в зависимости от параметра а ) имеет уравнение f(x) = a.

Девиз урока: «Решай, ищи, твори и мысли».

Ход урока:

1. Организационный момент.

Активизировать внимание, объявить тему и цель урока.

Вводное слово учителя:

Вы уже накопили некоторый опыт исследования функций и построения графиков функций. Сегодня мы рассмотрим изученный материал с более общих позиций. Все задачи объединены по сюжетному принципу.

Весьма важно уметь переформулировать задачу и за внешними различиями увидеть общую схему решения.

2. Повторение теоретического материала.

1. Как находить экстремумы функции?

Т4 (необходимое и достаточное условие существование экстремума)

Если f ´(х)=0, то х₀ - стационарная точка,

если f ´(х) не существует, то х₀ - критическая точка.

Т5 (достаточное условие существования экстремума)

а) x₀ - точка max

f '(x) + -

f (x) x₀x

б) x₀ - точка min

f ' (x) + -

f (x) x

в) x₀ - точка перегиба

f ' (x) + - f '(x) - + _________________________________ x __________________________________x

f (x) f(x)

3. Исследование функции по графику производной.

Задачи ЕГЭ (группа В)

Функция y=f(x) определена на промежутке [-6;3]. График производной изображен на рисунке.

у y=f ' (x)

f ' (x) _ + _ + _

_______●______________●__________●______________●______________________

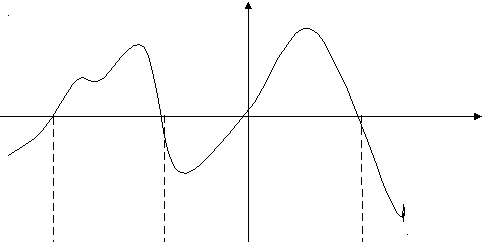
f (x) -5 -2 0 2

Задания для учащихся .

1) Изобразить схематически знаки производной на промежутке области определения:

2. Как называются точки -5, -2, 0, 2 ?

3. Ответить на вопросы:

   • Укажите число точек максимума. ( х_max=-2, х_min=2). Ответ: 2.

   • Найти число точек экстремумов. Ответ: 4.

   • Укажите число точек минимума функции. (x_min=-5, x_min=0) Ответ:2.

   • Укажите число промежутков возрастания функции. [-5;-2],[0;2]. Ответ: 2.

   • Укажите количество точек графика функции, в которых касательная параллельна оси ОХ. -5; -2; 0; 2 . Ответ: 4.

   • Найдите наибольшую из длин промежутков убывания функции. [-2;0] Ответ: 2.

   • Укажите количество промежутков убывания функции. Ответ: 3.

   • Найдите суммарную длину промежутков возрастания функции. (3+2=5) Ответ: 5.

   • Укажите количество интервалов убывания функции. Ответ: 3.

4. Схема исследования свойств функции и построение графика функции.

Пример 1. а) Построить график функции y=5x³ - 3x⁵

б) Для каждого значения параметра а решить уравнение.

Решение:

а) у=5х³ - 3х⁵

1).D(y) = (- ∞; +∞).

2). Функция нечетная.

3.)Нули функции: у=0 х³ ( 5 - 3х²) = 0,

х = 0, х = ±

4). Промежутки монотонности :

у ' = 15х² - 15 х⁴ ,

у ' = 0, 15х² (1 - х²) = 0

х = 0, х = ±1 - стационарные точки.

у '(х) - + + -

______________________________________________

у(х) -1 0 1 х

х_min =-1, x_max=1, x=0 -точка перегиба

у_min = у(- 1)= - 5 + 3 = - 2

y_max = y(1) = 5 - 3 =2

y(0) = 0

5). Построим график функции:

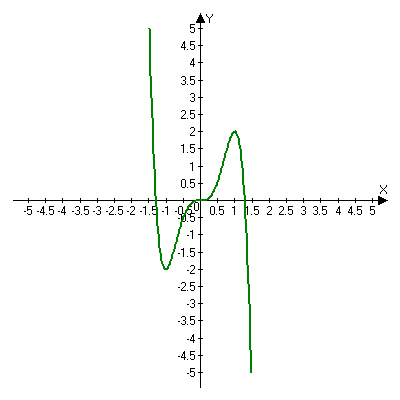
б). Решим уравнение: 5х³ - 3х² = а графически:

Пусть y= 5x³ -3x², y = a.

При а (-∞; -2) (2;∞) уравнение имеет 1 корень;

при а = -2, а = 2 уравнение имеет 2 корня;

при а уравнение имеет 3 корня.

5. Задачи централизованного тестирования.

1. Найдите количество точек экстремума функции у=0,6х⁵-1,5х⁴+х³+4.

Ответы: 1) 0 2) 1 3) 2 4) 4 5)5

у ' = 3х⁴ - 6х³ + 3х² Решение:

у ' + + + х

3х² (х² - 2х + 1) = 0 __________________________

х² (х - 1)² = 0 у 0 1

Нет экстремумов

Ответ: 1

2. Найдите длину промежутка убывания функции у=3х⁵-5х³+1.

Ответы: 1) 0 2) 1 3) 2 4) 4 5) 5

Решение :

у ' =15х⁴ - 15х²

15х² (х² -1) = 0

х=0 - корень четной кратности

у ' + - - +

___________________________________

у - 1 0 1

х = ± 1

Промежуток убывания [-1; 1], длина промежутка 2.

Ответ: 3

3. Найдите количество точек экстремумов функции у = 3х⁵ - 15х².

Ответы: 1) 0 2) 1 3) 2 4) 3 5) 4

Решение:

у ' =15х⁴ - 30х

15х ( х³ - 2) = 0 у ' + - +

х = 0, х =- точки экстремумов ___________________________________ х

у

Ответ : 3

4. Найдите значение функции у = 2х² - в точке минимума.

Ответы: 1) - 2) - 3) - 4) - 5) 0

Решение:

у ' =4х -

=0, 8х^3/2 - 1 =0, х > 0, х =

у_min = у() = 2 - = - = -

у ' - +

_________○________________●__________х

у 0

Ответ: 2

5. Найдите количество точек экстремума функции у = .

Ответы: 1) 1 2)2 3) 3 4) 4 5) 0

Решение:

у =- +

у ' = - =0

х = ± 1 - стационарная точка

х = 0 - критическая точка

у ' + - - +

_______________●______○______●_______ х х_max = -1, х_min = 1

у

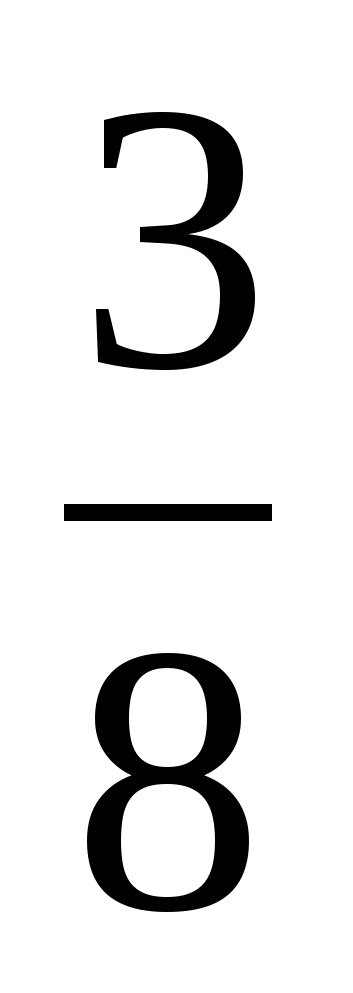
-1 0 1

Ответ: 2

6. Найдите точку минимума функции у = (х -1 )² .

Ответы: 1)0 2) 1 3) 2 4) 3 5)

Решение:

у ' =2 (х -1) + ОДЗ. х > 0

=0; = 0;

5х² - 6х +1 = 0 х ₁= 1, х₂ = - стационарные точки, х = 0 - критическая точка

х > 0

у ' + - +

__________○________●________●________х х_min = 1

у 0 1

Ответ: 2

7. Найти количество точек экстремумов функции у = .

Ответы: 1)2 2) 3 3) 1 4) 0 5) 4

Решение:

у = - +

у ' = - , =0

х = ± 3 - стационарные точки

х = 0 - критическая точка четной кратности

у ' + - - +

____________●________○_________●_______ х х_max = -3, x_min = 3

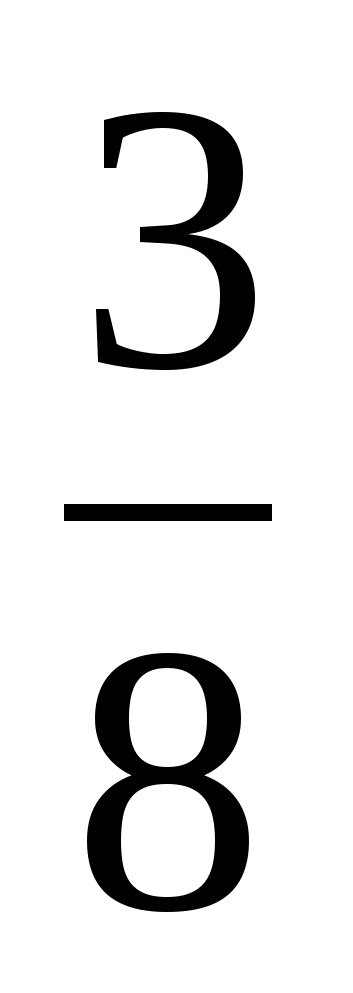
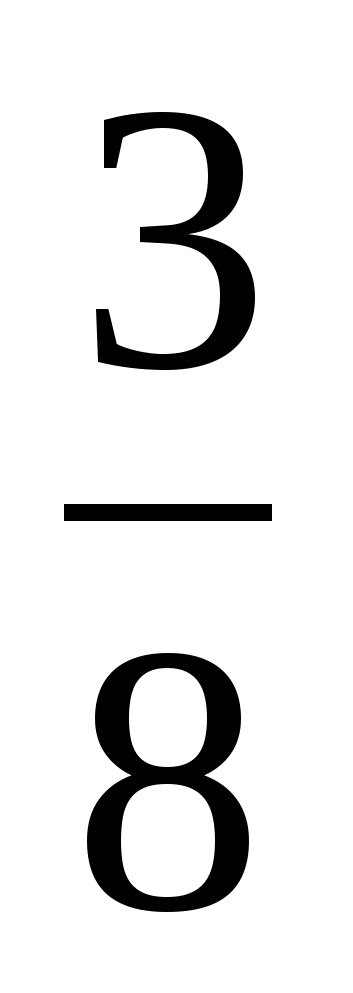
у -3 0 3

Ответ: 1

8. Найдите точку максимума функции у = (х -1)⁴ .

Ответы: 1) 0 2) 3) 4) 5) 1

Решение:

у ' =4 (х - 1)³ + ; =0; =0

х = 1, х = - стационарные точки

х = 0 - критическая точка (х > 0)

у ' + - +

______○_________●_________●_________х х_max =

у 0 1

Ответ: 4

6. Итоги урока.

• Повторили условия существования экстремума.

• По графику производной находили промежутки монотонности функции, определяли характер экстремумов.

• По графику функции, построенному с применением производной, исследовали, сколько решений может иметь уравнение, содержащее параметр.

• Познакомились с заданиями централизованного тестирования.

Приложения.

1. Найдите количество точек экстремума функции у=0,6х⁵ -1,5х⁴+х³+4.

Ответы: 1) 0 2) 1 3) 2 4) 4 5)5

2. Найдите длину промежутка убывания функции у=3х⁵-5х³+1.

Ответы: 1) 0 2) 1 3) 2 4) 4 5) 5

3. Найдите количество точек экстремумов функции у = 3х⁵ - 15х².

Ответы: 1) 0 2) 1 3) 2 4) 3 5) 4

4. Найдите значение функции у = 2х² - в точке минимума.

Ответы: 1) - 2) - 3) - 4) - 5) 0

5. Найдите количество точек экстремума функции у = .

Ответы: 1) 1 2)2 3) 3 4) 4 5) 0

6. Найдите точку минимума функции у = (х -1 )² .

Ответы: 1)0 2) 1 3) 2 4) 3 5)

7. Найти количество точек экстремумов функции у = .

Ответы: 1)2 2) 3 3) 1 4) 0 5) 4

8. Найдите точку максимума функции у = (х -1)⁴ .

Ответы: 1) 0 2) 3) 4) 5) 1