Конспект урока по теме «Прямоугольник. Ромб. Квадрат» (8 класс)

Конспект урока

Решение задач по теме: «Прямоугольник. Ромб. Квадрат»

8 класс

Урок геометрии - это, во-первых, знание теории и, во - вторых, правильное и разумное применение этой теории на практике. Данный урок - это урок систематизации и обобщения полученных знаний и применение этих знаний на практике.

Цель урока: создать условия для развития умений решать задачи по теме «Прямоугольник. Ромб. Квадрат», применяя изученные определения и свойства.

Задачи урока:

1) создать условия для:

• закрепления знаний, умения и навыков учащихся по теме " Прямоугольник. Ромб. Квадрат ";

• обобщения и систематизации теоретических знаний учащихся по теме " Прямоугольник. Ромб. Квадрат ";

2. развивать внимание, память, логическое мышление; активизировать мыслительную деятельность, умение анализировать, обобщать и рассуждать;

3. воспитание трудолюбия, усердия в достижении цели, интерес к предмету.

Оборудование урока:

1. Схемы выпуклых четырехугольников (у каждого ученика на столах);

2. Карточки для слабых учеников;

3. Карточки с геометрическими фигурами;

4. Доска, разноцветный мел, разноцветные маркеры.

Тип урока: повторительно-обобщающий.

Орг.форма: традиционная.

План урока:

1. Организационный момент (3 мин.)

2. Устная работа, проверка домашнего задания (15 мин.)

3. Решение задач (20 мин.)

4. Итог урока (2 мин.)

Доска в начале урока:

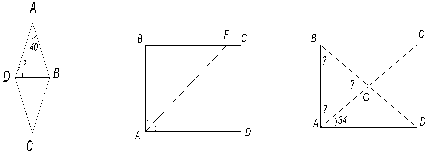1) 2) 3)

Ход урока:

1. Организационный момент:

В начале урока три ученика готовят домашнее задание на доске. Учитель сообщает тему и цель урока. Просит записать домашнее задание в дневник. Раздает карточки слабым ученикам.

Учитель:

Цель урока: обобщить и систематизировать знания и умения по теме: «Прямоугольник. Ромб. Квадрат.» Повторить определения и свойства выпуклых четырехугольников. Способы применения их к решению задач.

Домашнее задание: п. 45, 46; №432, 433,437(на дополнительную оценку).

2. Устная работа:

Свойства фигур показываются на доске учителем. Ученики отмечают эти свойства у себя на схемах (фронтальный опрос учащихся).

Учитель:

Какая фигура называется многоугольником?

Ученик:

Фигура, составленная из отрезков так, что смежные отрезки не лежат на одной прямой, а не смежные отрезки не имеют общих точек, называют многоугольником.

Учитель:

Какой многоугольник называется выпуклым?

Ученик:

Многоугольник называется выпуклым, если он лежит по одну сторону от каждой прямой, проходящей через две его соседние вершины.

Учитель:

Чему равна сумма углов выпуклого четырехугольника?

Ученик:

Сумма углов выпуклого четырехугольника равна 360⁰.

Учитель:

Дайте определение параллелограмма? Является ли параллелограмм выпуклым четырехугольником?

Ученик:

Параллелограммом называется четырехугольник, у которого противоположные стороны попарно параллельны.

Учитель:

Сформулируйте свойства параллелограмма.

Ученик:

1. В параллелограмме противоположные стороны равны и противоположные углы равны.

2. Диагонали параллелограмма точкой пересечения делятся пополам.

Учитель:

Сформулируйте признаки параллелограмма.

Ученик:

1. Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник - параллелограмм.

2. Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник - параллелограмм.

3. Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник - параллелограмм.

Учитель:

Какой четырехугольник называется прямоугольником?

Какими свойствами обладает прямоугольник?

Ученик:

Прямоугольником называется параллелограмм, у которого все углы прямые.

В прямоугольнике противоположные стороны равны, а диагонали точкой пересечения делятся пополам.

Учитель:

Сформулируйте особое свойство прямоугольника.

Ученик:

Диагонали прямоугольника равны.

Учитель:

Сформулируйте признак прямоугольника.

Ученик:

Если в параллелограмме диагонали равны, то этот параллелограмм - прямоугольник.

Учитель:

Какой четырехугольник называется ромбом? Какими свойствами обладает ромб?

Ученик:

Ромбом называется параллелограмм, у которого все стороны равны.

В ромбе противоположные углы равны и диагонали точкой пересечения делятся пополам.

Учитель:

Сформулируйте особое свойство ромба.

Ученик:

Диагонали ромба взаимно перпендикулярны и делят его углы пополам.

(1 ученик на доске по чертежу доказывает это свойство. Остальные ученики внимательно слушают и задают дополнительные вопросы.) (док-во на стр.105 п.46)

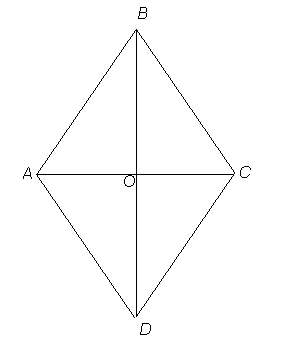Дано:

АВСD - ромб;

Док-ть:

ВD┴АС;

ВАС=САD; ВСА=DСА;

АВD=СВD; АDВ=СDВ.

Доказательство:

ΔАВС=ΔАDC (по трем сторонам) ВАС=САD; ВСА=DСА;

ΔАВD=ΔСВD (по трем сторонам) АВD=СВD; АDВ=СDВ.

ΔАВС - равнобедренный, ВО - медиана к стороне АС (т.к.диагонали ромба точкой пересечения делятся пополам) ВО - высота ВD┴АС.

Учитель:

Проверяем решение задачи №407.

Найдите углы, которые образуют диагонали ромба с его сторонами, если один из углов ромба 45⁰.

Ученик:

(2 ученик объясняет решение задачи)

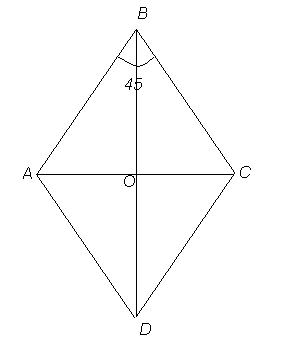Дано:

АВСD - ромб;

В=45⁰;

Найти:

АВD=?

ВАС=?

Учитель:

Проверяем решение задачи №412.

Даны равнобедренный прямоугольный треугольник АВС с прямым углом С, катетом АС=12см и квадрат CDEF, такой, что две его стороны лежат на катетах, а вершина Е- на гипотенузе треугольника. Найдите периметр квадрата.

Ученик:

(3 ученик объясняет решение задачи)

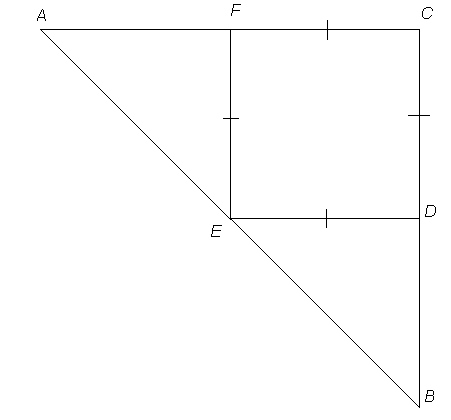
Дано:

ΔАСВ;

АС=ВС;

С=90⁰;

АС=12 см.

Найти:

периметр квадрата.

Решение:

ΔАСВ - прямоугольный и равнобедренный (по условию)А=В=45⁰ (сумма острых углов прямоугольного треугольника 90⁰). Проведем диагональ СЕ. ΔСЕА - прямоугольный и равнобедренный, т.к. А= АСЕ=45⁰ (диагонали квадрата делят углы пополам). EF - высота в равнобедренном ΔСЕА, проведенная к основанию АС EF- медиана AF=FC=12:2=6 см. периметр квадрата равен 24 см.

Учитель:

Какой четырехугольник называется квадратом?

Ученик:

Квадратом называется прямоугольник, у которого все стороны равны.

Квадратом называется ромб, у которого все углы прямые.

Учитель:

Сформулируйте основные свойства квадрата.

Ученик:

1. Все углы квадрата прямые.

2. Диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делятся пополам и делят углы квадрата пополам.

Учитель:

(учитель последовательно показывает карточки с фигурами: ромб, квадрат, прямоугольник, трапеция, параллелограмм)

Нарисуйте в тетради фигуры в той последовательности, в которой я вам их показала. Зачерните лишнюю фигуру. Объясните, почему вы ее зачеркнули.

3. Решение задач:

Задачи решаются устно.

1. Дано: АВСD - ромб, А = 40⁰. Найдите ВDA.

2. Дано: АВСD - прямоугольник, AF - биссектриса ВА D. Определите вид треугольника АВF и его углы.

3. Дано: АВСD - прямоугольник, СА D =34⁰. Найдите:

   • углы ΔАОВ;

   • углы между диагоналями. (см. рис. на доске)

Решение задач из учебника.

№436, 437 (резерв).

№436 (рассматриваем различные способы решения)

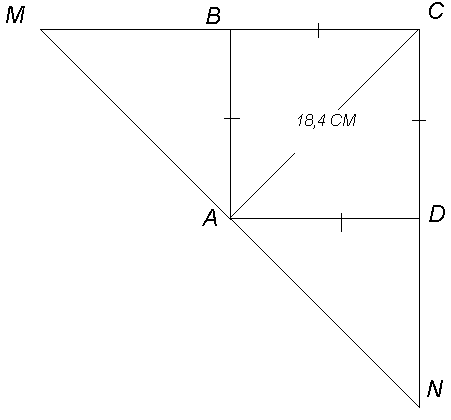
Дано:

АВСD - квадрат;

АС=18,4 см;

MN ┴ АС.

Найти: MN.

Решение:

Рассмотрим прямоугольные треугольники АСМ и АСN:

АС - общая сторона;

АСМ = АСN (т.к. диагонали квадрата делят углы пополам).

треугольники равны по катету и прилежащему острому углу. Из равенства треугольников следует равенство сторон МА и NА. Треугольники АСМ и АСN - равнобедренные, т.к. углы при основаниях равны (АМС=АСМ=45⁰; АNС=АСN=45⁰. Сумма острых углов прямоугольного треугольника равна 90⁰)

МА=АN=АС=18,4 см. MN=2АС=18,4·2=36,8см.

4. Итог урока.

Повторить определения и свойства прямоугольника, ромба и квадрата.

Выставление оценок.