Метод проблемного обучения на уроках математики в современной школе.

МЕТОД ПРОБЛЕМНОГО ОБУЧЕНИЯ НА УРОКАХ МАТЕМАТИКИ В СОВРЕМЕННОЙ ШКОЛЕ.

Т. И. Гуляева

Негосударственное образовательное учреждение «Школа-интернат №20 среднего (полного) общего образования ОАО РЖД» г. Омска

«Каждый человек видит тем больше нерешённых проблем, чем обширнее круг его знаний» С.Л.Рубинштейн

Обучение школьников ставить вопросы (проблемы) - важнейший фактор роста качества обучения, средство подготовки к творчеству, труду.

Умственное воспитание предполагает:

• овладение школьниками знаниями;

• овладение умениями правильно оперировать полученными знаниями, логически мыслить;

• развитие инициативы, умения принимать решения, не останавливаться на достигнутом;

• формирование творческого отношения к труду;

• формирование мотивов умственной деятельности.

Уровень развития умственных способностей всегда определяет способность правильно мыслить, достигать успехов в решении проблем. Задача учителя- научить школьника не только понимать, но и мыслить. Для этого надо развивать способности школьников. Это развитие обеспечивает возможность самостоятельно овладевать знаниями. Но умственная деятельность должна быть, прежде всего, мотивирована. Необходимы аргументы средства, побуждающие школьника активно действовать на уроке. У Плутарха есть известная притча о работниках, которые везли тачки с камнями. Работников было трое. К ним подошёл человек и задал каждому и них один и тот же вопрос: «Чем ты занимаешься?» Ответ первого был таков: «Везу эту проклятую тачку». По иному ответил второй: «Зарабатываю себе на хлеб». Третий воодушевлённо провозгласил: «Строю прекрасный храм!» Все они выполняли одну и ту же работу, но думали о ней, а, следовательно, и выполняли её по-разному. Поэтому, прежде всего, необходимо осознание школьниками полезности своего учебного труда, осознание мотивов своей деятельности. Конечно, в основе умственных способностей лежат природные задатки человека. Задача учителя в том и состоит, чтобы развить эти задатки.
Как известно, проблемой называют задачу, которую невозможно разрешить с помощью известных знаний и способов действий. Она обычно выглядит как противоречие, возникающее в ходе развития познания. Многие педагоги суть проблемного обучения видят в противоречии между знаниями и отсутствием необходимых знаний. Но тогда возникает вопрос: «Каков путь от незнания к знанию?». Если он лежит через заучивание, то здесь и проблемы нет. Но если для усвоения нового материала необходимы самостоятельные поиски, связанные с исследованием предметов и явлений, с выявлением их связей, изменений, то есть возникает проблемная ситуация, то здесь требуется напряжение умственной деятельности.

Можно выделить три группы проблемных ситуаций:

А. Познавательные (теоретическое мышление);
Б. Оценочные (критическое мышление);
В. Организаторско-производственные (практическое мышление).

Познавательные проблемы решаются сравнением, выдвижением гипотез, предположений и т.д. В результате появляются новые законы и выводы в науке, новые понятия…
Оценочные проблемы требуют критической оценки предметов и результатов труда.
Решение организаторско-производственных проблем связано с поиском путей различных положительных изменений окружающей действительности и способствует развитию практического мышления, а также ведёт к поиску применения знаний на практике.

Рассмотрим подробнее некоторые ситуации.

А. На каждом уроке возможно привлекать учащихся к самостоятельному определению понятий. На основании наблюдений, описаний ученики выделяют существенные признаки предмета или явления. Например, учащиеся усвоили понятие «прямоугольник» и переходят к изучению квадрата. Необходимо определить понятие «квадрат». На доске учитель нарисовал несколько квадратов разных по размерам, положению, цвету. Нужно установить, что общего во всех этих фигурах, дать определение понятия «квадрат». После многократного повторения этот приём закрепляется в сознании школьника как способ определения понятия, как средство познания окружающей действительности. Главное в решении познавательной проблемы - привлечь школьников к решению данной проблемы, заинтересовать их новой деятельностью.

Сравнение выступает как самостоятельная проблема: сравни геометрические фигуры, сравни выражения и т. д. Сравнение помогает глубже понять предметы и явления. С помощью сравнения устанавливается сходство и различие предметов и явлений по определенным признакам. Например, выявить сходство и различие между параллелограммом и ромбом, дать определение ромбу через понятие параллелограмма. Заполняя таблицу сходств и различий четырехугольников, учащиеся на долго запоминают свойства этих фигур.

Б. Основная цель организации оценочных проблемных ситуаций - развитие критического мышления учащихся. Нет такой области жизни, где бы не приходилось оценивать предметы и явления. Умение правильно, критически мыслить необходимо всем людям. Обычно на уроке учащимся приходится опровергать ложные суждения. В процессе этой работы они должны проявить высокую наблюдательность и путём сопоставления найти ошибку.

Примеры заданий:

• равным наклонным соответствуют равные наклонные;

• если произведение двух чётных чисел чётное число, то и сумма этих чисел чётное число;

• биссектриса угла в равнобедренном треугольнике есть одновременно его высота и медиана;

• в цветочном магазине продавали 67 роз. Красных было на 4 больше, чем белых. Сколько было красных и белых роз отдельно?

Необходимо развивать у школьников способность к анализу, умению находить ошибки и обосновывать их. Прививать школьникам эти навыки надо постепенно: сначала научить определять суждение, в котором имеется ошибка, затем подбирать аргументы, опровергающие ошибки и, наконец, развёрнуто и последовательно строить опровержение. Опровергнуть суждение - значит установить его ложность; приводимый аргумент должен точно соответствовать логическим законам, правилам. Можно использовать различные приемы для поиска ошибок: взаимопроверка, рецензирование и диспут.

В. Учебные организаторско -производственные ситуации способствуют подготовке учащихся к активной деятельности в производстве, развивают практическое мышление, учат находить выход из возможных трудных положений. На уроках по различным предметам можно и необходимо готовить учащихся к труду, к выбору профессии, учить решать проблемы, которые возникают в процессе практической деятельности. Знания учащихся становятся более глубокими и прочными, обогащаются новыми фактами.

Объяснение нового материала является эффективным, если содержание передаваемой информации и форма её подачи обеспечивают необходимую активность учащихся, и от того, как учитель организует объяснение, во многом зависит качество их знаний. Параграфы по геометрии начинаются сразу с определения или формулировки теоремы, поэтому самой приходится продумывать вводные замечания, связывать данную тему с предыдущей, создавать проблемные ситуации, подыскивать материал, который бы заинтересовал учащихся. Например, урок, посвящённый трапеции, можно начать сразу с определения, а можно начать так:
«Приходилось ли вам слышать слово «трапеция» раньше? Знаете ли вы, что оно означает?
Сегодня на уроке мы узнаем, какая фигура в геометрии называется трапецией и каковы её свойства, чем она отличается от четырехугольников, изученных ранее». А можно начать урок с изображения на доске различных выпуклых четырёхугольников. Среди них известные ребятам параллелограмм, прямоугольник, квадрат, ромб и новый четырёхугольник (трапеция). Учащимся предлагается назвать их и дать определение, а неизвестный четырёхугольник назвать « трапецией» и попросить учащихся дать самим определение (учащиеся должны увидеть параллельность только двух сторон).

Возьмём урок «Теорема Пифагора». Начать можно с исторических сведений, рассказать о Пифагоре, а уж затем перейти к доказательству самой теоремы. Изложение исторического материала занимает немного времени и способствует повышению интереса к изучаемой теме. И всё же наиболее целесообразным является вариант, предусматривающий создания проблемной ситуации: «Рассмотрим задачу. В прямоугольном треугольнике катеты равны 4 и 3 сантиметра. Чему равна гипотенуза этого треугольника?» Потом продолжаем: «Пока вы не можете решить такую задачу. Это не удивительно, так как для её решения необходимо знать очень важную теорему, с которой мы и познакомимся».
Предлагая учащимся задачу, решение которой возможно только с применением теоремы Пифагора, мы тем самым ставим проблему, как найти гипотенузу, зная катеты треугольника. Благодаря созданной проблемной ситуации, восприятие нового материала делается осознанным, целенаправленным, что способствует его глубокому усвоению.

Или вот урок по теме: « Формула корней квадратного уравнения» Учитель: Вы знаете, что математика одна из древнейших наук. В Древней Индии были распространены публичные соревнования по решению трудных задач. Задачи часто представлялись в стихотворной форме. Вот одна из таких задач:

Обезьянок резвых стая
Всласть, поевши, развлекалась.
Их в квадрате часть восьмая
На поляне забавлялась.
А двенадцать по лианам
Стали прыгать, повисая…
Сколько ж было обезьянок,
Ты скажи мне, в этой стае?

Далее по тексту задачи составляется уравнение и выясняется, что такое уравнение учащиеся решать не умеют.

Урок 1. Тема: « Формула корней квадратного уравнения»

Учитель: Вы знаете, что математика одна из древнейших наук. В Древней Индии были распространены публичные соревнования по решению трудных задач. Задачи часто представлялись в стихотворной форме. Вот одна из таких задач:

Обезьянок резвых стая
Всласть, поевши, развлекалась.
Их в квадрате часть восьмая
На поляне забавлялась.
А двенадцать по лианам
Стали прыгать, повисая…
Сколько ж было обезьянок,
Ты скажи мне, в этой стае?

Далее по тексту задачи составляется уравнение. При этом учащиеся могут допустить сами или учитель может спровоцировать следующую ошибку:. После проверки окончательно получаем уравнение . Это уравнение вида ax² + bx + c = 0. Далее выясняется. Почему оно называется квадратным, являются ли квадратными уравнения вида ax² + bx = 0, ax² + c = 0, bx + c = 0.
Возникает проблема, как решать такие уравнения?
Затем рассматриваются предлагаемые учащимся пути решения неполных квадратных уравнений, предпринимаются безуспешные попытки решения полного уравнения , записанного в общем виде ax² + bx + c = 0.
Вынесение общего множителя x(ax + b) + c = 0 по аналогии с решением уравнения ax² + bx = 0, или перенос свободного члена ax² + bx = - c по аналогии с уравнением ax² + c = 0 не приносят желаемых результатов. Все попытки решения обсуждаются. Если ученики высказывают сомнение можно ли решить эту задачу вообще, учитель предъявляет им уравнение , которое ребята способны решить и в котором после проведённых преобразований «узнают» исходное уравнение. Один из вариантов решения предлагает учитель. Он сообщает, что в древности, когда геометрия была более развита. чем алгебра . такие уравнения решали не алгебраически, а геометрически. Вот, например, как древние решали уравнение .

Рассмотрим рисунок 1.

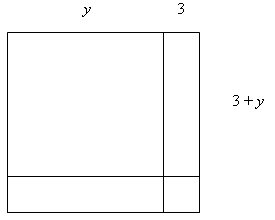
Рисунок 1

Решение представлено на этом рисунке. Это решение следует сопроводить записями: y + 3 = 5, откуда y = 2.
y + 3, как в уравнении y + 3 = 5 появляется число 5; что сделано с обеими частями уравнения; где на рисунке добавленное к обеим частям равенства число 9; является ли число - 8 корнем исходного уравнения; в ходе какой операции потерян этот корень; почему древние греки были обречены его потерять?

Затем выясняется, что выражение y² + y + 9 и 16 + 9 геометрически представляют собой один и тот же квадрат, а исходное уравнение и уравнение y² + 6y - 16 + 9 - 9 = 0 - одно и то же уравнение, откуда и получаем, что y + 3 = ±5.
Далее учитель выделяет новую проблему: как изобразить ситуацию геометрически, если второй коэффициент в уравнении отрицателен? Например, пусть уравнение имеет вид
y² - 6y - 16 = 0.
По аналогии с рассмотренной выше ситуацией, на рисунке появляются квадраты со сторонами y и y - 3. Если учащиеся, исходя из рисунка 2, предлагают рассмотреть равенство
y² = (y - 3)² + 6(y - 3) + 9, то после преобразований получим 0 = 0. На вопрос, почему последняя запись не позволила продвинуться в решении уравнения, следует ответ, что эта запись - алгебраическое тождество и в нём не использовано условие, что y² - 6y - 16 = 0. Преобразуя последнее равенство, получаем y² - 6y = 16. На рисунке 2 находим «изображение» выражения y² - 6y, и обращаем внимание, что в нём из площади квадрата со стороной y два раза вычитается площадь квадрата со стороной 3.

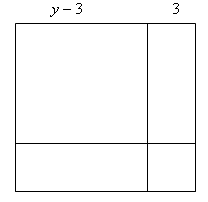
Рисунок 2

Значит, если к выражению y² - 6y прибавить 9, то получим площадь квадрата со стороной y - 3.
Заменяя выражение y² - 6y равным ему числом 16, получим (y - 3)² = 16 + 9, т.е. y - 3 = ± = ± 5.
Далее возникает очередная подпроблема: как представить рассмотренные решения квадратных уравнений в краткой алгебраической форме, обоб щив геометрические решения.
В результате такого обобщения получаем метод выделения полного квадрата.

Приведенный пример удовлетворяет всем требованиям проблемного обучения:

а) Изучение темы начинается с ситуации невозможности решить практическую задачу, обнаруженную в старинных рукописях.
б) Проблема разбивается на ряд подпроблем.
в) Решению проблемы способствует рассмотрение истории решения квадратных уравнений.
г) На уроке показаны два способа решения уравнения - геометрический и алгебраический.
д) В беседе рассмотрен ряд гипотез, не приведших к решению и ошибочные шаги.
е) Исторический материал естественно «вплетается» в содержание урока, делая его живым и занимательным.

Урок 2. Тема: «Теорема Пифагора»

Учитель предлагает решить задачу: На охоте с двух отвесных скал два охотника заметили козла и одновременно в него выстрелили, причём стрелы достигли цели одновременно. Охотники одновременно начали спуск к добыче с одинаковой скоростью (см. рис. 3).

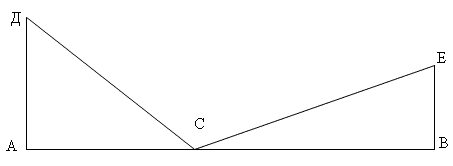
Рисунок 3

Проблемная ситуация возникает при построении математической модели практической задачи. Она рассматривается с помощью вопросов. Как на чертеже изображаются:

1) скалы?
2) расстояние между ними?
3) путь каждой стрелы?
4) путь каждого охотника?
5) что означает факт, что стрелы достигли цели одновременно?

Анализ задачи позволяет заключить, что на данном этапе задачу решить нельзя, так как невозможно использовать равенство отрезков ДС и СЕ, которые являются гипотенузами прямоугольных треугольников. Если бы зависимость между катетами и гипотенузой в прямоугольном треугольнике была известной, то можно было бы в каждом треугольнике выразить гипотенузу через катеты и приравнять полученные выражения.

ВОЗНИКАЕТ ПРОБЛЕМА:

Существует ли зависимость между гипотенузой и катетами в прямоугольном треугольнике, и, если она существует, то как она формулируется?
Для решения этой проблемы учитель организует поиск формулировки, предложив учащимся задание по группам:
Построить прямоугольные треугольники с катетами 3 и 4, 12 и 5, 6 и 8, 8 и 15 и измерить гипотенузу. Результаты заносятся в таблицу.

Далее выдвигаются и обсуждаются различные гипотезы.

Верно ли, что a + , если это справедливо для первого и третьего случая?

Верно ли, что a = , если это справедливо для четвёртого случая?

Если учащиеся не увидят существующей зависимости, то учитель продолжает заполнять таблицу, находя квадраты соответствующих значений.
Следующая проблема возникает при доказательстве. Можно использовать различные доказательства, известные из истории математики. После доказательства теоремы Пифагора, возвращаемся к исходной задаче. В заключении этого урока можно предложить учащимся следующий вопрос:
В Древнем Египте после разлива Нила требовалось восстановить границы земельных участков, для чего на местности необходимо было строить прямые углы. Египтяне поступали следующим образом: брали верёвку , завязывали на равных расстояниях узлы и строили треугольники со сторонами 3,4 и 5 таких отрезков. Правильно ли они поступали?