Разработка урока на тему:Классическое определение теории вероятностей

Урок на тему: «Введение классического определения теории вероятностей»

Цели:

образовательные:

• ввести определения и формулы для вычисления вероятностей (с первичным закреплением), дать краткий исторический очерк;

• научить ребят решать задачи на вычисление вероятностей с применением формул комбинаторики;

развивающие:

• формирование формально-логического мышления;

• развитие восприятия, памяти;

воспитательные:

• побуждать к преодолению трудностей в процессе умственной деятельности.

Оборудование: карточки с условиями задач, листочки для самостоятельной работы.

Тип урока: урок объяснения нового материала.

Вид урока: комбинированный урок-беседа и урок решения задач.

Метод: эвристический.

Ход урока

I. Организационный момент

II. Проверка выполнения домашнего задания

Опрос. Фронтально. (Повторение формул комбинаторики)

а) Сколько чисел можно записать с помощью цифр 1, 2, 3, 4 при условии, что все цифры различны. Что такое перестановки из n элементов, и как они считаются?

б) Пять человек участвуют в конкурсе. Сколькими способами им можно присудить первые три места? Что такое размещения из n элементов по k, и по какой формуле они считаются?

в) Сколькими способами можно выбрать 5 дежурных с первого ряда? Что такое сочетания из n элементов по k, и по какой формуле они считаются?

III. Обеспечение мотивации учебно-познавательной деятельности, актуализация знаний

В обыденной жизни, давая какие-либо прогнозы, мы нередко употребляем выражения "вероятность", "вероятно". Например, глядя утром в окно "Вероятно, сегодня будет дождь. К истории не готовился - вероятно будет 2. По литературе, вероятно, спросят… "и т.д.

Причём мы отдаём себе отчёт, в каких событиях "мало" вероятности, в каких - "много".

Маловероятно, что сегодня не будет алгебры… Невероятно, самостоятельной на физике не было!

Над проблемой численной оценки этой вероятности работали многие учёные, но только в ХХ веке, в основном благодаря трудам нашего соотечественника А.Н. Колмогорова, были построены математические основы теории вероятностей.

IV. Усвоение новых знаний

Давайте разберёмся, что же такое - случайное событие?

Выбираете билет на экзамене. Попадёт вам 16 счастливый билет или нет - случайное событие

Вызовут вас к доске на уроке или нет - случайное событие.

Выиграете вы в лотерее или нет - случайное событие.

Определение:

Случайное событие - которое может либо произойти, либо не произойти при одних и тех же условиях.

Далее работа по карточкам:

1. Найдите случайные и закономерные события.

1. При нагревании проволоки её длина увеличивается.

2. При бросании игральной кости выпадут 4 очка.

3. При бросании монеты выпадет герб.

4. При осмотре почтового ящика найдены три письма.

Определение:

Достоверным называется событие, которое происходит при каждом эксперименте.

2. Выберите достоверные события.

1. Два попадания при трёх выстрелах.

2. Получение пятёрки на экзамене.

3. Наугад выбранное случайное число не больше 1000.

4. Наугад выбранное число, составленное из цифр 1, 2, 3 без повторений, меньше 400.

Определение:

Невозможным называется событие, которое никогда не происходит.

3. Назовите невозможные события:

1. Отмена урока алгебры.

2. Появление слова "мама" при случайном наборе букв м, м, а, а.

3. Появление Толика в классе за 15 минут до звонка на 1 урок.

4. Появление 19 очков при бросании трёх игральных костей.

Кроме случайного события, с опытом связано ещё одно понятие - элементарное событие.

Определение:

Элементарное событие (исход) - один из взаимоисключающих вариантов, которым может завершиться случайный эксперимент.

Рассмотрим число исходов в следующих опытах:

Опыт 1: Бросание монеты.

Опыт 2: Бросание кубика.

Ω - множество исходов опыта

ω - исход опыта, элемент множества

ωΩ

АΩ

Рассмотрим пример на кубике: А={2, 4, 6}

Невозможное событие - 0, достоверное событие - Ω

Что же называется непосредственно "вероятностью" какого-либо события?

Французский естествоиспытатель Ж.Л.Л. Бюффон в XVIII столетии подбрасывал монету 4040 раз - герб выпал 2048 раз. Математик К. Пирсон в начале прошлого века подбрасывал её 24000 раз - герб выпал 12012 раз.

Значит, результаты бросаний монеты, хотя каждое из них и является случайным событием, при неоднократном повторении подвластны объективному закону.

Рассмотрим случайный эксперимент А,

n - равновозможные исходы, (примеры 1, 2, 3)

m - благоприятные исходы, (зависит от задачи)

Р(А)= - вероятность события.

Вероятность случайного события - это число из промежутка [0, 1].

Определение:

События называются равновозможными, если нет оснований полагать, что при многократном повторении этого испытания чаще наступит одно событие, чем другое.

А={} p(A)=p()+…+p()

Бросаем игральную кость. Выпасть могут или одно, или два, или три, или четыре, или пять, или шесть очков. Каждое из этих событий - элементарное, и вместе они образуют пространство элементарных событий.

Для опытов с равновозможными исходами рассмотрим несколько задач:

4. Найдём количество благоприятных исходов и вероятность события при бросании кубика.

1. Выпало чётное число очков 3; 1/2

2. Выпало меньше 3 очков 2; 1/3

3. Выпало меньше 5 очков 4; 2/3

4. Выпало не меньше 3 очков 4.

5. Подбрасываем монету, найдём количество благоприятных исходов и вероятность события

1. Выпадет «орёл» - 1; 1/2.

2. Выпадет «решка» - 1; 1/2

6. Подбрасываем 2 монеты подряд, найдём количество благоприятных исходов и вероятность события

1. Обе упадут на «орла» - 1; 1/4

2. Обе упадут на «решку» - 1; 1/4

3. Упадут на одинаковую сторону - 2; 1/2

Более возможно то событие, которому благоприятствует большее число равновозможных событий.

V. Проверка усвоения материала (самостоятельная работа с проверкой)

1 вариант

1. В ящике имеется 4 белых и 7 чёрных шаров. Какова вероятность того, что наудачу вытянутый шар окажется белым?
   
   Решение: Здесь m = 4, n = 11. Поэтому Р = .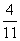

2. Если событие достоверное, то чему равна его вероятность?
   
   Вероятность достоверного события равна 1.

3. Какова вероятность невозможного события?
   
   Она равна нулю.

4. Кубик подбрасывают один раз. Какова вероятность появления четырёх очков?
   
   Р = .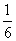

2 вариант

1. В ящике имеется 5 синих ручек и 7 чёрных. Какова вероятность того, что наудачу вытянутая ручка окажется синей?
   
   Решение: Здесь m = 5, n = 12. Поэтому Р =.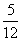

2. Какова вероятность невозможного события?
   
   Она равна нулю.

3. Если событие достоверное, то чему равна его вероятность?
   
   Вероятность достоверного события равна 1.

4. Кубик подбрасывают один раз. Какова вероятность появления чётных очков?
   
   Р = .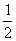

Анализ самостоятельной работы, подведение итога урока.

VI. Домашнее задание :

1. Из колоды в 36 карт случайным образом вытаскивают 3 карты. Найти вероятность того, что
   
   а) нет пиковой дамы,
   
   б) есть пиковая дама.

2. Случайно выбрали двузначное число. Найдите вероятность того, что оно
   
   а) оканчивается 0;
   
   б) состоит из одинаковых цифр;
   
   в) больше 27 и меньше 46;
   
   г) не является квадратом числа.