Урок в 10 классе по 'Тригонометрические функции'

10 класс

Тема урока: Функция y=cos(x) ее свойства и график.

Цель: 1) Повторить и закрепить свойства функции y=sin(x), навыки решения уравнений графическим способом, выполнение преобразований графика функции;

2) Изучить свойства функции у=cos(x), выработать умения изображать график схематически и по графику находить область определения и область значения функции, промежутки возрастания и убывания, знакопостоянства, нули функции, минимальное и максимальное значения;

3) выработать навыки применения полученных знаний при решении уравнений графическим способом, вычисления значения функции и выполнение преобразований графика у=cos(x)

Оборудование: графики, интерактивная доска, проектор, чертежные инструменты

Ход урока:

1. орг момент.

I этап

1) обращение к опорному конспекту и числовой окружности.

2) проверка домашнего задания ( слайд чистый работают карандашами)

3) вычислить:

a) ;

б)

в)

г)

4. Как построить график функции с помощью графика функции y=sin(x)

Какая точка является началом вспомогательной системы координат

II формирование новых знаний.

А) формулировка темы урока

Б) определяем цели урока

5. постройте график функции y=sin(x+п/2) (этапы построения диаграмм в эт)

Как построить график функции y=cos(x) (учащиеся рассуждают, обратить внимание на график построенной функции y=sin(x+п/2) преобразовать выражение, что получилось)

Вызываем к доске учащегося добавляем столбец с функцией y=cos(x) строим два графика одновременно (какой вывод)

Вывод: y=sin(х+п/2)= cos(x) и следовательно построенный в начале график функции и есть график функции косинус

Попробуйте самостоятельно по графику перечислить свойства функции y=cos(x)

1. D(f)=

2. y=cos(x) четная, так как график симметричен ОУ и cos(-x)= cos(x)

3 убывает ,

возрастает

4. периодична основной период Т=

5 ограничена сверху у=1 снизу у= - 1

6 у наименьшее = -1 в точке х=

у наибольшее = 1 в точке х=

7. непрерывна

8. E(f)=

9 выпукла вверх

выпукла вниз

Где применяются графики функций y=cos(x) и y=sin(x) (ученики: при решении уравнений и неравенств, систем уравнений и систем неравенств)

Пример 1 решить уравнение cos(x) - х² -1=0

cos(x)= х² +1

разбиваем на 2 функции y=cos(x) и у= х² +1

строим в эт графики этих функций и находим точку пересечения графиков (в случае необходимости уменьшаем шаг изменения аргумента).

Пример 2. решить графически уравнение cos(x)=х+п/2 (х=п/2)

Пример 3 решить графически уравнение cos(x)=2х-2п (x=5п/6)

Построить и прочитать и прочитать график кусочной функции

Одновременно по карточкам индивидуально работают несколько сильных учащихся. Они выполняют номер 16.67 (а,б)

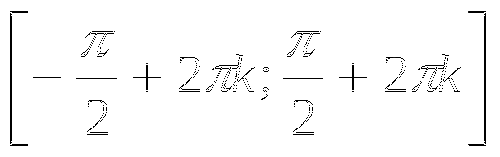
Показать применение логических функций в построении графика

Устно перечисляются свойства функции

1. D(f)=

2. четность ,не является ни четной ни нечетной

3 терпит разрыв в точке х=0

4. возрастание и убывание бесконечно меняется

5. у _{наименьшее} = -1

у _{наибольшее} = 1

6. E(f)=

7 не периодична.

III закрепление

Проверка индивидуальных графиков

16.67

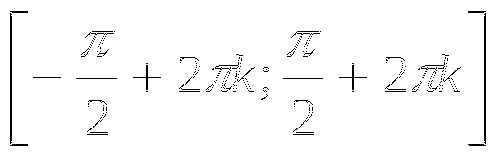
А)

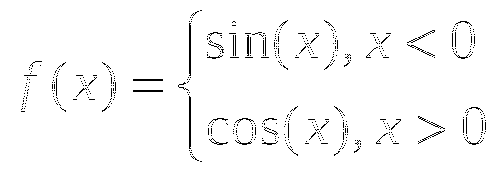
Б)

№ 16.14, 16,43 устно

№ 1614 найти по графику область значений

Y=sin(x) E(f)=[-1;1]

Y=cos(x)

16.43 по графику выяснить монотонность y=cos(x) на промежутке

- возрастает

- возрастает убывает

Выполнить самостоятельно по рядам

1 ряд у=2sinx 2 ряд y=-3cosx + 2 3 ряд y=5+4cosx

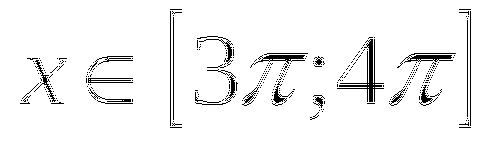
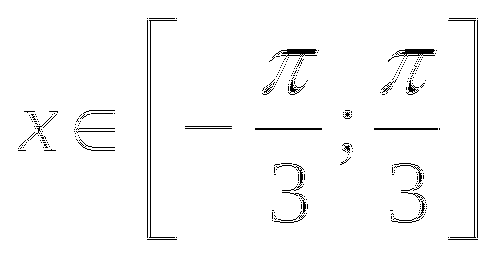
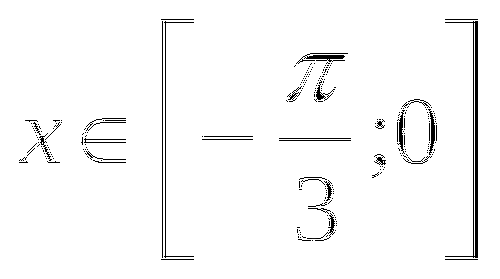
ЗАДАЧА: сколько целочисленных значений функции?

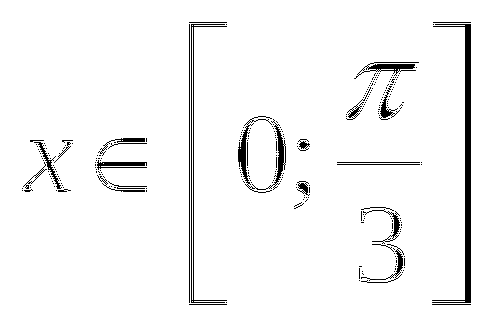
у доски работают три ученика

16.36 Известно, что f(x)=3sin(x) найдите

a) f(-х); б)2f(x) в) 2f(x)+1 г)f(-x)+f(x)

16.37 Известно, что f(x)=0,5cos(x) найдите

a) f(-х); б)2f(x) в) f(x+2п)+1 г)f(-x)-f(x)

16.38 Известно, что f(x)=сos(x/3) найдите

a) f(-х); б)3f(x) в) f(-3x) г)f(-x)-f(x)

16.41 (а) делают самостоятельно

IV Домашнее задание

Задается домашнее задание с комментированием

16.49(в) 16.52(а) 16.53(а,б)

Дополнительно 16.59(а,б)

Тестовая работа

1. н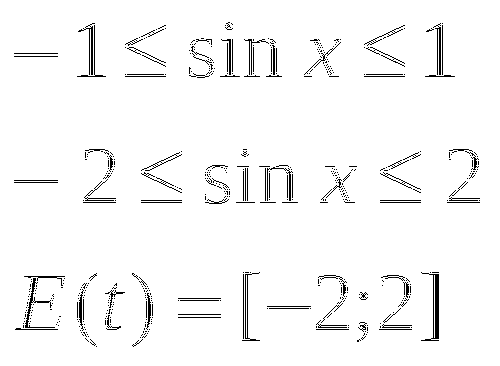айдите значение

a) б)-1 в)1 г)

2. Не выполняя построений ответьте на вопрос: какая из указанных точек с координатами принадлежит графику

y=cos(x) y=sin(x)

1. б) в) г)

3. Найти E(f)

Y=3cos(x)-2 y=3cos(x)+2

А) [-5;1] б)[-3;-2] в)[-3;2] г)[-1;5]

4. К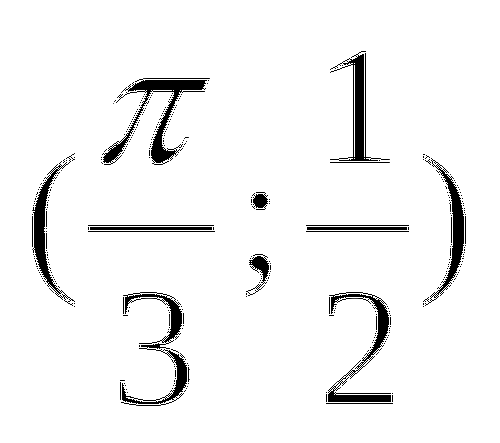акая из указанных точек является началом координат вспомогательной системы координат для построения графика

А) б) в) г)

5. Сколько корней имеет система уравнений

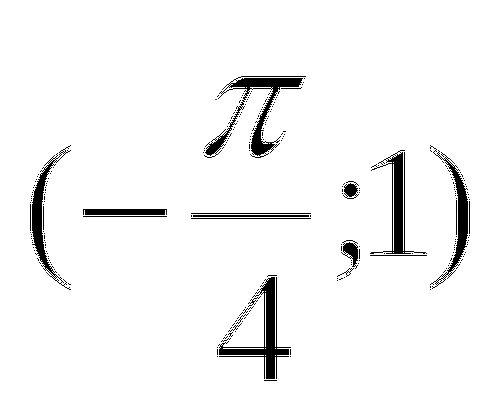
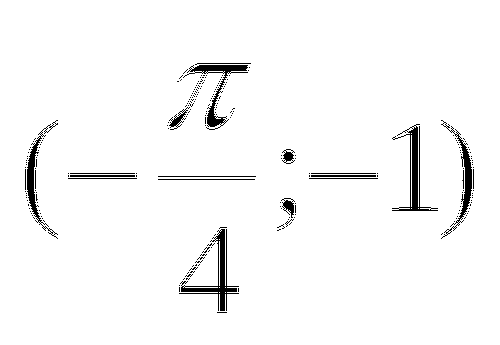
V Подведение итогов

Вопрос ученикам:

1. Какую тему мы изучали? (ответ учеников)

2. Какова цель урока ?

3. Чему научились?

4. Какие новые знания вы для себя приобрели?

5. Какого типа упражнения с помощью графика у=cos(x) , y=sin(x) вы можете выполнять