- Учителю
- Рабочая программа 7 класс
Рабочая программа 7 класс
7 класс.
1 .Пояснительная записка.
Рабочая программа по математике для 7 класса составлена в соответствии со следующими нормативно-правовыми документами:
· Федеральный компонент Государственного образовательного стандарта общего образования, утверждённым приказом Минобразования России от 05.03.2004 г. №1089 «Об утверждении федерального компонента государственных стандартов начального общего, основного общего и среднего (полного) общего образования»;
·Федеральные требования к образовательным учреждениям в части минимальной оснащённости учебного процесса и оборудования учебных помещений, утверждённые приказом Министерства образования и науки РФ от 04.10.2010 г. №986;
·Приказ Минобрнауки России от 19.12.2012 №1067 «Об утверждении федеральных перечней учебников, рекомендованных (допущенных) к использованию в образовательном процессе в образовательных учреждениях, реализующих образовательные программы общего образования и имеющих государственную аккредитацию, на 2013/2014 учебный го».
·Региональный (национально-региональный) компонент государственного образовательного стандарта дошкольного, начального общего, основного общего и среднего (полного) общего области от 17 января 2006 г. N15-ПП;
·Образовательная программа МБОУ СОШ № 22, утверждённая приказом директора от 17.05.2012 г. №2774
Рабочая программа позволяет всем участникам образовательного процесса получить представление о целях, содержании, общей стратегии обучения, воспитания и развития учащихся средствами данного учебного предмета. А также предусматривает выделение этапов обучения, структурирование учебного материала, определение его количественных и качественных характеристик на каждом из этапов, в том числе для содержательного наполнения промежуточной аттестации учащихся.
В ходе освоения содержания курса учащиеся получают возможность:
∙развить представления о числе и роли вычислений в человеческой практике; сформировать практические навыки выполнения устных, письменных, инструментальных вычислений, развить вычислительную культуру;
∙ овладеть символическим языком алгебры, выработать формально-оперативные алгебраические умения и научиться применять их к решению математических и нематематических задач;
∙ изучить свойства и графики элементарных функций, научиться использовать функционально-графические представления для описания и анализа реальных зависимостей;
развить пространственные представления и изобразительные умения, освоить основные факты и методы планиметрии, познакомиться с простейшими пространственными телами и их свойствами;
получить представления о статистических закономерностях в реальном мире и о различных способах их изучения, об особенностях выводов и прогнозов, носящих вероятностный характер;
∙ развить логическое мышление и речь - умения логически обосновывать суждения, проводить несложные систематизации, приводить примеры и контрпримеры, использовать различные языки математики (словесный, символический, графический) для иллюстрации, интерпретации, аргументации и доказательства;
∙сформировать представления об изучаемых понятиях и методах как важнейших средствах математического моделирования реальных процессов и явлений.
Курс алгебры построен в соответствии с традиционными содержательно-методическими линиями: числовой, функциональной, алгоритмической, уравнений и неравенств, алгебраических преобразований. В курсе алгебры 7-го класса продолжается систематизация сведений о преобразовании выражений и решении уравнений с одним неизвестным. Продолжается изучение степени с натуральным показателем. Изучаются свойства функций 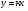 и ее график. Главное место занимают алгоритмы действий с многочленами - сложение, вычитание и умножение. Особое внимание уделяется разложению многочленов на множители с помощью вынесения за скобки общего множителя и с помощью группировки. Вырабатываются умения применять формулы сокращенного умножения как для преобразования произведения в многочлен, так и для разложения на множители. Даются первые знания по решению систем линейных уравнений с двумя переменными, что позволяет значительно расширить круг текстовых задач. Серьезное внимание уделяется формированию умений рассуждать, делать простые доказательства, давать обоснования выполняемых действий. Параллельно закладываются основы для изучения систематических курсов стереометрии, физики, химии и других смежных предметов.
и ее график. Главное место занимают алгоритмы действий с многочленами - сложение, вычитание и умножение. Особое внимание уделяется разложению многочленов на множители с помощью вынесения за скобки общего множителя и с помощью группировки. Вырабатываются умения применять формулы сокращенного умножения как для преобразования произведения в многочлен, так и для разложения на множители. Даются первые знания по решению систем линейных уравнений с двумя переменными, что позволяет значительно расширить круг текстовых задач. Серьезное внимание уделяется формированию умений рассуждать, делать простые доказательства, давать обоснования выполняемых действий. Параллельно закладываются основы для изучения систематических курсов стереометрии, физики, химии и других смежных предметов.
Для более широкого знакомства с математикой введен курс «Элементы статистики и теории вероятностей».На этом этапе продолжается решение задач путем перебора возможных вариантов, изучается статистический подход к понятию вероятности. Дается классическое определение вероятности, формируются умения вычислять вероятности с помощью формул комбинаторики. Особое внимание уделяется правилу сложения вероятностей.
Данное планирование определяет достаточный объем учебного времени для повышения математических знаний учащихся в среднем звене школы, улучшения усвоения других учебных предметов.
В курсе геометрии 7-го класса расширяются сведения о геометрических фигурах. На начальном этапе основное внимание уделяется двум аспектам: понятию равенства геометрических фигур (отрезков и углов) и свойствами измерения отрезков и углов. Главное место занимают признаки равенства треугольников. Формируются умения выделять равенство трех соответствующих элементов данных треугольников и делать ссылки на изученные признаки. Особое внимание уделяется доказательству параллельности прямых с использованием соответствующих признаков. Теорема о сумме углов треугольника позволяет получить важные следствия, что существенно расширяет класс решаемых задач. Серьезное внимание уделяется формированию умений рассуждать, делать простые доказательства, давать обоснования выполняемых действий. Параллельно закладываются основы для изучения систематических курсов стереометрии, физики, химии и других смежных предметов
Рабочая программа по математике для 7 классов обеспечивает реализацию государственного образовательного стандарта основного общего образования базового уровня.
Изучение математик основного общего образования базового уровня направлено на достижение следующих целей:
Цель обучения: формирование математического аппарата для решения задач из математики и смежных предметов.
Задачи обучения:
-
овладение системой математических знаний и умений, необходимых для применения практической деятельности изучения смежных дисциплин, продолжения образования;
-
овладение навыками дедуктивных рассуждений;
-
интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе: ясность и точность мысли, критичность мышления, интуиция, логическое мышление, элементы алгоритмической культуры, необходимой, в частности, для освоения курса информатики;
-
формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;
-
получение школьниками конкретных знаний о функциях как важнейшей математической модели для описания и исследования разнообразных процессов (равномерных, равноускоренных, экспоненциальных, периодических и т.д.);
-
воспитание культуры личности, отношения к математике как части общечеловеческой культуры, понимание значимости математики для научно технического прогресса;
-
развитие представлений о полной картине мира, о взаимосвязи математики с другими предметами.
Общая характеристика учебного предмета
Содержание математического образования в основной школе формируется на основе фундаментального ядра школьного математического образования. В программе оно представлено в виде совокупности содержательных разделов, конкретизирующих соответствующие блоки фундаментального ядра применительно к основной школе.
Содержание математического образования в VII классе включает следующие разделы:алгебра, функции, геометрия. Содержание каждого из этих разделов разворачивается в содержательно-методическую линию, пронизывающую все основные разделы содержания математического образования на данной ступени обучения.
Содержание раздела «Алгебра» направлено на формирование у учащихся математического аппарата для решения задач из разных разделов математики, смежных предметов, окружающей реальности. Язык алгебры подчеркивает значение математики как языка для построения математических моделей процессов и явлений реального мира. В задачи изучения алгебры входят также развитие алгоритмического мышления, необходимого, в частности, для усвоения курса информатики, овладения навыками дедуктивных рассуждений. Преобразование символьных форм вносит специфический вклад в развитие воображения учащихся, их способностей к математическому творчеству. В основной школе материал группируется вокруг рациональных выражений.
Содержание раздела «Функции» нацелено на получение школьниками конкретных знаний о функции как важнейшей математической модели для описания и исследования разнообразных процессов. Изучение этого материала способствует развитию у учащихся умения использовать различные языки математики (словесный, символический, графический), вносит вклад в формирование представлений о роли математики в развитии цивилизации и культуры.
Цель содержания раздела «Геометрия» - развить у учащихся пространственное воображение и логическое мышление путем систематического изучения свойств геометрических фигур на плоскости и в пространстве и применения этих свойств при решении задач вычислительного и конструктивного характера. Существенная роль при этом отводится развитию геометрической интуиции. Сочетание наглядности со строгостью является неотъемлемой частью геометрических знаний.
Результаты изучения учебного предмета
Изучение математики в VII классе дает возможность обучающимся достичь следующих результатов развития:
1) в личностном направлении:
• умение ясно, точно, грамотно излагать свои мысли в устной и письменной речи, понимать смысл поставленной задачи, выстраивать аргументацию, приводить примеры и контрпримеры;
• критичность мышления, умение распознавать логически некорректные высказывания, отличать гипотезу от факта;
• представление о математической науке как сфере человеческой деятельности, об этапах ее развития, о ее значимости для развития цивилизации;
• креативность мышления, инициатива, находчивость, активность при решении математических задач;
• умение контролировать процесс и результат учебной математической деятельности;
• способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений;
2) в метапредметном направлении:
• первоначальные представления об идеях и о методах математики как универсальном языке науки и техники, средстве моделирования явлений и процессов;
• умение видеть математическую задачу в контексте проблемной ситуации в других дисциплинах, в окружающей жизни;
• умение находить в различных источниках информацию, необходимую для решения математических проблем, представлять ее в понятной форме, принимать решение в условиях неполной и избыточной, точной и вероятностной информации;
• умение понимать и использовать математические средства наглядности (графики, диаграммы, таблицы, схемы и др.) для иллюстрации, интерпретации, аргументации;
• умение выдвигать гипотезы при решении учебных задач, понимать необходимость их проверки;
• умение применять индуктивные и дедуктивные способы рассуждений, видеть различные стратегии решения задач;
• понимание сущности алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом;
• умение самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем;
• умение планировать и осуществлять деятельность, направленную на решение задач исследовательского характера;
3) в предметном направлении:
• овладение базовым понятийным аппаратом по основным разделам содержания, представление об основных изучаемых понятиях (число, геометрическая фигура, уравнение, функция) как важнейших математических моделях, позволяющих описывать и изучать реальные процессы и явления;
• умение работать с математическим текстом (анализировать, извлекать необходимую информацию), грамотно применять математическую терминологию и символику, использовать различные языки математики;
• умение проводить классификации, логические обоснования, доказательства математических утверждений;
• умение распознавать виды математических утверждений (аксиомы, определения, теоремы и др.), прямые и обратные теоремы;
• развитие представлений о числе и числовых системах от натуральных до действительных чисел, овладение навыками устных, письменных, инструментальных вычислений;
• овладение символьным языком алгебры, приемами выполнения тождественных преобразований рациональных выражений, решения уравнений, систем уравнений, умение использовать идею координат на плоскости для интерпретации уравнений, систем, умение применять алгебраические преобразования, аппарат уравнений для решения задач из различных разделов курса;
• овладение системой функциональных понятий, функциональным языком и символикой, умение на основе функционально-графических представлений описывать и анализировать реальные зависимости;
• овладение геометрическим языком, умение использовать его для описания предметов окружающего мира, развитие пространственных представлений и изобразительных умений, приобретение навыков геометрических построений;
• усвоение систематических знаний о плоских фигурах и их свойствах, а также на наглядном уровне - о простейших пространственных телах, умение применять систематические знания о них для решения геометрических и практических задач;
• умения измерять длины отрезков, величины углов, использовать формулы для нахождения периметров, площадей и объемов геометрических фигур;
• умение применять изученные понятия, результаты, методы для решения задач практического характера и задач из смежных дисциплин с использованием при необходимости справочных материалов, калькулятора, компьютера.
2. Учебно-тематический план
-
№
Наименование разделов
Всего часов
В том числе
Самостоятеная
работа
теоретические
лабораторные
котрольные
1
Алгебраические выражения
10
1
2
Начальные геометричные сведения
10
1
3
Уравнение с одним неизвестным
8
1
4
Треугольники
17
1
5
Одночлены и многочлены
17
1
6
Разложение многочленов на множители
17
1
7
Алгебраические дроби
20
1
8
Параллельные прямые
13
1
9
Линейная функция
10
1
10
Системы двух уравнений с двумя переменными
11
1
11
Соотношение между сторонами и углами треугольника
18
2
12
Введение в комбинаторику
7
13
Повторение
12
всего
170
12
Содержание тем учебного курса математика (170 часов)
-
№
п\п
Тема, количество часов
Содержание.
Требования к результату обучения
Характеристика основных видов
деятельности ученика
(на уровне учебных действий).
1
Алгебраические выражения.
( 10 часов )
Числовые выражения. Алгебраические выражения. Формулы. свойства арифметических действий. Правила раскрытия скобок.
Знает, понимает:
-
понятия: « алгебраическое выражение», «значение алгебраического выражения», « числовое выражение», «значение числового выражения», « допустимые значения переменных, входящих в алгебраическое выражение»;
-
правила раскрытия скобок;
-
порядок выполнения действий в числовых выражениях;
-
законы сложения и умножения (переместительный, сочетательный, распределительный).
Умеет:
-
составлять буквенные выражения и формулы по условиям задач;
-
осуществлять в выражениях и формулах числовые подстановки и выполнять соответствующие вычисления;
-
выражать из формул одни переменные через другие;
Применяет полученные знания:
-
для выполнения расчетов по формулам;
-
для составления формул, выражающих зависимости между реальными величинами.
Выполнять элементарные знаково-символические действия: применять буквы для обозначения чисел, для записи общих утверждений; составлять буквенные выражения по условиям, заданным словесно, преобразовывать алгебраические суммы и произведения (выполнять приведение подобных слагаемых, раскрытие скобок, упрощение выражений). Вычислять числовое значение буквенного выражения. Составлять формулы, выражающие зависимости между величинами, вычислять по формулам.
2
Начальные геометрические сведения
(11 часов)
Точка, прямая, плоскость. Понятие о геометрическом месте точек. Часть прямой (отрезок, луч), угол. Отрезок прямой, как кратчайший путь между двумя точками. Расстояние. Длина отрезка. Угол. Прямой угол. Острые и тупые углы. Вертикальные и смежные углы. Биссектриса угла. Градусная мера угла. Перпендикулярность прямых.
Знать: какие фигуры называются равными; свойства измерения отрезков и углов; определение вертикальных и смежных углов, их свойства.
Уметь: Распознавать на чертежах и моделях геометрические фигуры (отрезки, углы, лучи, прямые). Изображать указанные геометрические фигуры, выполнять чертежи по условию простейших задач по теме «Вертикальные и смежные углы».
Применять: Владеть практическими навыками использования геометрических инструментов для нахождения длин отрезков и величин углов. Использовать их при решении простейших задач
Объяснять, что такое отрезок, луч. Угол, какие фигуры называются равными. Как сравниваются и измеряются отрезки и углы, что такое градус и градусная мера угла, какой угол называется прямым, тупым, острым, развернутым, что такое середина отрезка и биссектриса угла, какие углы называются смежными и вертикальными; формулировать и обосновывать утверждения о свойствах смежных и вертикальных углов; объяснять какие прямые называются перпендикулярными; формулировать и обосновывать утверждение о свойстве двух прямы, перпендикулярных третьей прямой; изображать и распознавать указанные простейшие фигуры на чертежах; решать задачи. Связанные с этими простейшими фигурами.
3
Уравнения с одним неизвестным.
( 8 часов )
Уравнение и его корни. Уравнения с одним неизвестным, сводящиеся к линейным. Решение задач с помощью уравнений.
Знает, понимает:
-
понятия: « уравнение», « корень уравнения», « решить уравнение»;
-
свойства уравнений;
-
алгоритм решения уравнения.
Умеет:
-
решать линейные уравнения;
-
решать текстовые задачи алгебраическим методом.
Применяет полученные знания:
для решения задач
Проводить доказательные рассуждения о корнях уравнения с опорой на определение корня, числовые свойства выражений. Распознавать линейные уравнения. Решать линейные, а также уравнения сводящиеся к ним. Решать простейшие уравнения с неизвестным под знаком модуля. Решать текстовые задачи алгебраическим способом: переходить от словесной формулировки условия задачи к алгебраической модели путём составления уравнения; решать составленное уравнение; интерпретировать результат.
4
Треугольники,
( 17 часов)
Внутренние и внешние углы треугольника. Стороны треугольника, его медиана, биссектриса и высота. Остроугольные, прямоугольные и тупоугольные треугольники. Равнобедренные треугольник, его свойства и признаки. Равносторонний треугольник. Признак равенства
треугольников. Центр, радиус, диаметр
окружности и круга. Хорда и дуга.
Знать определение и свойства, признаки равных треугольников; определение медианы, высоты и биссектрисы треугольника, перпендикуляра к прямой.
Знать определение и свойства равнобедренного треугольника.
Уметь доказывать равенство треугольников, т.е. выделять равенство трех соответствующих элементов данных треугольников и делать ссылки на изученные признаки (с помощью учителя и самостоятельно).
Применять их при решении простейших задач.
Объяснять, какая фигура называется треугольником, что такое вершины, стороны, углы и периметр треугольника, какой треугольник называется равнобедренным, равносторонним; какие треугольники называются равными; изображать распознавать на чертежах треугольники и их элементы; формулировать и доказывать теоремы о признаках равенства треугольников; объяснять, что называется перпендикуляром, проведенным из данной точки к данной прямой; формулировать и доказывать теорему о перпендикуляре к прямой; объяснять, какие отрезки называются медианой, биссектрисой и высотой треугольника; формулировать и доказывать теоремы о свойствах равнобедренного треугольника; решать задачи, связанные с применением признаков равенства треугольников и свойствами равнобедренного треугольника; формулировать определение окружности; объяснять, что такое центр, радиус, хорда и диаметр окружности; решать простейшие задачи на построение (построение угла, равного данному, построение биссектрисы угла, построение перпендикулярных прямых, построение середины отрезка) и более сложные задачи, использующие указанные простейшие; сопоставлять полученный результат с условием задачи; анализировать возможные случаи.
5
Одночлены и многочлены.
( 17 часов )
Степень с натуральным показателем и её свойства. Одночлен. многочлен. Сложение, вычитание и умножение многочленов. Деление одночлена и многочлена на одночлен.
Знает, понимает:
-
понятия: «степень с натуральным показателем», «многочлен», «одночлен», «стандартный вид одночлена»;
-
свойства степени с натуральным показателем;
-
правила действий с одночленами и многочленами (кроме деления многочлена на многочлен);
Умеет:
-
выполнять основные действия с многочленами и одночленами;
-
выполнять основные действия со степенями;
-
приводить одночлен и многочлен к стандартному виду.
Формулировать, записывать в символической форме и обосновывать свойства степени с натуральным показателем; применять свойства степени для преобразования выражений и вычислений. Выполнять действия с одночленами и многочленами. Применять различные формы самоконтроля при выполнении преобразований выражений.
6
Разложение многочлена на множители.
( 17 часов )
Вынесение общего множителя за скобки. Способ группировки. Формулы сокращенного умножения:
(a + b)(a - b)=(a2 - b2),
(
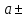 b)2 = a2
b)2 = a2 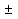 2ab+b2.
2ab+b2.
Знает, понимает:
-
формулы сокращенного умножения;
-
смысл «разложить на множители»;
-
алгоритм разложения многочлена на множители.
Умеет:
выполнять разложение многочлена на множители.
Применяет полученные знания:
для упрощения выражений
Доказывать формулы сокращенного умножения, применять их в преобразованиях выражений и вычислениях.
Выполнять разложение многочленов на множители разными способами. Выполнять разложение многочленов на множители с помощью формул куба суммы, куба разности, суммы кубов, разности кубов. Решать уравнения, применяя свойство равенства нулю произведения. Применять различные формы самоконтроля при выполнении преобразований.
7
Алгебраические дроби.
( 20 часов )
Алгебраическая дробь. Сокращение дробей. Сложение, вычитание, умножение и деление алгебраических дробей. Совместные действия над алгебраическими дробями.
Знает, понимает:
-
понятия: « алгебраическая дробь», « допустимые значения алгебраической дроби», « сокращение алгебраической дроби»;
-
смысл сходства действий над алгебраическими и обыкновенными дробями;
-
правила выполнения основных действий с алгебраическими дробями.
Умеет:
-
выполнять основные действия с алгебраическими дробями.
Применяет полученные знания:
для решения задач
Формулировать основное свойство алгебраической дроби и применять его для преобразования дробей. Выполнять действия с алгебраическими дробями. Находить допустимые значения букв, входящих в алгебраическую дробь. Решать уравнения, сводящиеся к линейным с дробными коэффициентами. Выполнять совместные действия над выражениями, содержащими алгебраические дроби.
8
Параллельные прямые,
( 13 часов)
Параллельность прямых, признаки и свойства параллельных прямых
Знать как называются углы при пересечении двух прямых секущей, определения, признаки, свойства и аксиому параллельных прямых.
Уметь доказывать параллельность прямых, используя соответствующие признаки, находить равные углы при параллельных прямых и секущей,
Применять теоремы для
обоснования способов построения параллельных прямых.
Формулировать определение параллельных прямых; объяснять с помощью рисунка, какие углы, образованные при пересечении двух прямых секущей, называются накрест лежащими, какие односторонними и какие соответственными; формулировать и доказывать теоремы, выражающие признаки параллельности прямых; объяснять, что такое аксиомы геометрии и какие аксиомы уже использовались ранее; формулировать аксиому параллельных прямых и выводить следствия из нее; формулировать и доказывать теоремы о свойствах параллельных прямых, обратные свойствам параллельных прямых, в связи с этим объяснять, что такое условие и заключение теоремы, какая теорема называется обратной по отношению к данной теореме; объяснять, в чем заключается метод доказательства от противного; приводить примеры использования этого метода; решать задачи на вычисление, доказательство и построение, связанные с параллельными прямыми.
9
Линейная функция и её график.
( 10 часов )
Прямоугольная система координат на плоскости. Понятие функции. Способы задания функций. График функции. Функция y=kx и её график. Линейная функция и её график.
Знает, понимает:
-
понятия: «функция», « функциональная зависимость», « независимая переменная», « график функции»;
-
способы задания функций;
-
влияние коэффициента k на расположение графика функции y=kx, y=kx+b.
Умеет:
-
находить значения функции, заданной формулой, таблицей, графиком по её аргументу;
-
находить значения аргумента по значению функции, заданной таблицей или графиком;
описывать свойства изученной функции, строить её график.
Вычислять значения функций, заданных формулами (при необходимости использовать калькулятор ); составлять таблицы значений функции. Описывать свойства функции на основе её графического представления. Моделировать реальные зависимости, выражаемые линейной функцией, с помощью формул и графиков. Интерпретировать графики реальных зависимостей. Использовать функциональную символику для записи разнообразных фактов, связанных с линейной функцией, обогащая опыт выполнения знаково-символических действий. Строить речевые конструкции с использованием функциональной терминологии. Использовать компьютерные программы для исследования положения на координатной плоскости графика линейной функции в зависимости от значений коэффициентов, входящих в формулу. Распознавать линейную функцию. Показывать схематически положение на координатной плоскости графиков функций вида y = kx, y = kx + b в зависимости от значений коэффициентов, входящих в формулы. Строить график функции y =
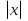 . Строить график линейной функции; описывать её свойства. Распознавать прямую и обратную пропорциональные зависимости. Решать текстовые задачи на прямую и обратную пропорциональные зависимости (в том числе с контекстом из смежных дисциплин, из реальной жизни).
. Строить график линейной функции; описывать её свойства. Распознавать прямую и обратную пропорциональные зависимости. Решать текстовые задачи на прямую и обратную пропорциональные зависимости (в том числе с контекстом из смежных дисциплин, из реальной жизни). 10
Системы двух уравнений с двумя неизвестными.
( 11 часов )
Система уравнений с двумя неизвестными. Решение системы уравнений первой степени с двумя неизвестными способами подстановки и сложения, графическим способом. Решение задач методом составления систем уравнений.
Знает, понимает:
-
понятия: «система уравнений», «система линейных уравнений с двумя неизвестными»;
-
основные способы решения систем уравнений с двумя неизвестными.
Умеет:
-
решать системы двух линейных уравнений;
-
решать текстовые задачи алгебраическим методом.
Применяет полученные знания:
для решения задач
Определять, является ли пара чисел решением данного уравнения с двумя неизвестными; приводить примеры решений уравнений с двумя неизвестными. Строить графики уравнений с двумя неизвестными, указанных в содержании. Находить целые решения систем уравнений с двумя неизвестными путём перебора. Решать системы двух уравнений первой степени с двумя неизвестными. Решать текстовые задачи, алгебраической моделью которых является уравнение с двумя неизвестными: переходить от словесной формулировки условия задачи к алгебраической модели путём составления системы уравнений; решать составленную систему уравнений; интерпретировать результат. Конструировать речевые высказывания, эквивалентные друг другу, с использованием алгебраического и геометрического языков. Использовать функционально- графические представления для решения и исследования уравнений и систем.
11
Введение в комбинаторику.
( 7 часов )
Исторические комбинаторные задачи. Различные комбинации с выбором из трёх элементов. Таблица вариантов. Правило произведения. Подсчет вариантов с помощью графов.
Знает, понимает:
-
Различные комбинации с выбором из трех элементов;
-
Таблицу вариантов;
-
Правила произведения;
-
Правила подсчета вариантов с помощью графов
Умеет:
-
Решает задачи на различные комбинации с выбором из трех элементов, на правило произведения;
-
Составляет таблицу вариантов
Подсчитывает количество вариантов с помощью графов
Применяет полученные знания:
для решения задач
Выполнять перебор всех возможных вариантов для пересчета объектов или комбинаций объектов. Применять правило комбинаторного умножения для решения задач на нахождение числа объектов, вариантов или комбинаций (диагонали многоугольника, рукопожатия, число кодов, шифров, паролей и т. п.). Подсчитывать число вариантов с помощью графов.
12
Соотношения между сторонами и углами треугольника,
( 18 часов)
Сумма углов треугольника. Неравенство треугольника. Соотношение между сторонами и углами треугольника. Перпендикуляр и наклонная. Прямоугольный треугольник, его признаки и свойства.
Знать:
определение остроугольных, тупоугольных, прямоугольных треугольников;
свойства и признаки равенства прямоугольных треугольников; теорему о сумме углов треугольника,
понятие расстояния от точки до прямой, между параллельными прямыми,
неравенство треугольника.
Понимать, что сторонами и углами в треугольнике существует взаимно однозначное соответствие.
Уметь решать задачи по теме «Сумма углов в треугольнике», задачи на построение треугольников с помощью циркуля и линейки. Применять их при решении простейших задач.
Формулировать и доказывать теорему о сумме углов треугольника и ее следствие о внешнем угле треугольника; проводить классификацию треугольников по углам; формулировать и доказывать теорему о соотношениях между сторонами и углами треугольника (прямое и обратное утверждение) и следствия из нее, теорему о неравенстве треугольника; формулировать и доказывать теоремы о свойствах прямоугольных треугольников; формулировать определения расстояния от точки до прямой, расстояния между параллельными прямыми; решать задачи на вычисление, доказательство и построение, связанные с соотношением между сторонами и углами треугольника и расстоянием между параллельными прямыми, при необходимости проводить по ходу решения дополнительные построения, сопоставлять полученный результат с условием задачи, в задачах на построение исследовать возможные случаи.
-
Требования к уровню подготовки учащихся.
В результате изучения курса математики 7-го класса учащиеся должны:
знать/понимать:
-
свойства степени с натуральным показателем;
-
определение одночлена и многочлена;
-
операции над одночленами и многочленами;
-
формулы сокращенного умножения;
-
способы разложения на множители;
-
определение алгебраической дроби, операции над ними;
-
линейную функцию и её свойства, график;
-
определение уравнения с одним неизвестным, корня уравнения, свойства с помощью которых решаются уравнения;
-
способы решения систем.
-
образом геометрия математического каким доказательства; приводить существо понятия примеры доказательств;
-
возникла из практических задач землемерия; примеры геометрических объектов и утверждения о них, важных для практики;
уметь:
-
составлять буквенные выражения и формулы по условиям задач, осуществлять в выражениях и формулах числовые подстановки и выполнять соответствующие вычисления, осуществлять подстановку одного выражения в другое; выражать из формул одну переменную через остальные;
-
выполнять основные действия со степенями с натуральным показателем, с многочленами; выполнять тождественные преобразования целых выражений; выполнять разложение многочленов на множители;
-
решать линейные уравнения и уравнения, сводящиеся к ним, системы двух линейных уравнений,
-
решать текстовые задачи алгебраическим методом, интерпретировать полученный результат, проводить отбор решений, исходя из формулировки задачи;
-
изображать числа точками на координатной прямой
-
определять координаты точки плоскости, строить точки с заданными координатами;
-
находить значение функции, заданной формулой, таблицей, графиком по ее аргументу; находить значение аргумента по значению функции, заданной графиком или таблицей;
-
описывать свойства изученных функций (y = kx + b, y = kx) и строить их графики.
-
пользоваться геометрическим языком для описания предметов окружающего мира;
-
распознавать геометрические фигуры, различать их взаимное расположение;
-
изображать геометрические фигуры; выполнять чертежи по условию задач; осуществлять преобразования фигур; распознавать на чертежах, моделях и в окружающей обстановке основные фигуры, изображать их;
проводить доказательные рассуждения при решении задач, используя известные теоремы, обнаруживая возможности для их использования; решать простейшие
планиметрические задачи
применять на практике для:
-
выполнения расчётов по формулам, составления формул, выражающих зависимость между реальными величинами; нахождения нужной формулы в справочных материалах
-
моделирования практических ситуаций и исследование построенных моделей с использованием аппарата алгебры; описания зависимости между физическими величинами соответствующими формулами при исследовании несложных практических ситуаций;
-
интерпретации графиков реальных зависимостей между величинами
· описания реальных ситуаций на языке геометрии;
· решения геометрических задач;
· решения практических задач, связанных с нахождением геометрических величин (используя при необходимости справочники и технические средства);
· построений геометрическими инструментами (линейка, угольник, циркуль, транспортир).
.
Календарно - тематическое планирование
-
№ п\п
Наименование темы
Дата
Коррекция
Алгебраические выражения, 10 часов
1
Числовые выражения
2
Числовые выражения
3
Алгебраические выражения
4
Алгебраические равенства. Формулы
5
Свойства арифметических действий
6
Свойства арифметических действий
7
Правила раскрытия скобок
8
Правила раскрытия скобок
9
Обобщение, систематизация и коррекция знаний.
10
Контрольная работа № 1 по теме «Алгебраические выражения»
Начальные геометрические сведения, 10 часов
11.
Прямая и отрезок.
12.
Луч и угол.
13.
Сравнение отрезков и углов.
14.
Измерение отрезков.
15.
Решение задач по теме «Измерение отрезков»
16.
Измерение углов
17.
Смежные и вертикальные углы
18.
Перпендикулярные прямые.
19.
Решение задач по теме «Перпендикулярные прямые»
20
Контрольная работа № 2. По теме «Начальные геометрические сведения»
Уравнения с одним неизвестным, 8 часов
21
Уравнение и его корни
22
Решение уравнений с одним неизвестным, сводящихся к линейным
23
Решение уравнений с одним неизвестным, сводящихся к линейным
24
Решение задач с помощью уравнений
25
Решение задач с помощью уравнений
26
Решение задач с помощью уравнений
27
Обобщение, систематизация и коррекция знаний.
28
Контрольная работа № 3 по теме «Уравнения с одним неизвестным»
Треугольники, 17 часов
29.
Треугольники
30.
Первый признак равенства треугольников.
31
Решение задач на применение первого признака равенства треугольников
32.
Медианы, биссектрисы и высоты треугольника
33
Равнобедренный треугольник. Свойства равнобедренного треугольника.
34.
Решение задач по теме «Равнобедренный треугольник».
35.
Второй признак равенства треугольников.
36
Решение задач на применение второго признака равенства треугольников.
37
Третий признак равенства треугольников.
38
Решение задач на применение третьего признака равенства треугольников.
39.
Окружность
40
Задачи на построение.
41
Задачи на построение.
42.
Решение задач на применение признаков равенства треугольников.
43
Решение задач.
44
Решение задач. Подготовка к контрольной работе.
45
Контрольная работа № 4 по теме: «Треугольники»
Одночлены и многочлены, 17 часов
46
Степень с натуральным показателем
47
Свойства степени с натуральным показателем
48
Свойства степени с натуральным показателем
49
Свойства степени с натуральным показателем
50
Одночлен. Стандартный вид одночлена
51
Умножение одночленов
52
Многочлены
53
Приведение подобных членов
54
Приведение подобных членов
55
Сложение и вычитание многочленов
56
Сложение и вычитание многочленов
57
Умножение многочлена на одночлен
58
Умножение многочлена на одночлен
59
Умножение многочлена на многочлен
60
Умножение многочлена на многочлен
61
Деление одночлена и многочлена на одночлен
62
Контрольная работа № 5 по теме «Одночлены и многочлены»
Разложение многочленов на множители, 17 часов
63
Вынесение общего множителя за скобки
64
Вынесение общего множителя за скобки
65
Способ группировки
66
Способ группировки
67
Способ группировки
68
Формула разности квадратов
69
Формула разности квадратов
70
Квадрат суммы. Квадрат разности
71
Квадрат суммы. Квадрат разности
72
Квадрат суммы. Квадрат разности
73
Применение нескольких способов разложения многочлена на множители
74
Применение нескольких способов разложения многочлена на множители
75
Применение нескольких способов разложения многочлена на множители
76
Применение нескольких способов разложения многочлена на множители
77
Обобщение, систематизация и коррекция знаний.
78
Обобщение, систематизация и коррекция знаний.
79
Контрольная работа № 6 по теме «Разложение многочленов на множители»
Алгебраические дроби, 20 часов
80
Алгебраическая дробь. Сокращение дробей
81
Алгебраическая дробь. Сокращение дробей
82
Алгебраическая дробь. Сокращение дробей
83
Приведение дробей к общему знаменателю
84
Приведение дробей к общему знаменателю
85
Приведение дробей к общему знаменателю
86
Сложение и вычитание алгебраических дробей
87
Сложение и вычитание алгебраических дробей
88
Сложение и вычитание алгебраических дробей
89
Умножение и деление алгебраических дробей
90
Умножение и деление алгебраических дробей
91
Умножение и деление алгебраических дробей
92
Умножение и деление алгебраических дробей
93
Совместные действия над алгебраическими дробями
94
Совместные действия над алгебраическими дробями
95
Совместные действия над алгебраическими дробями
96
Совместные действия над алгебраическими дробями
97
Обобщение, систематизация и коррекция знаний.
98
Обобщение, систематизация и коррекция знаний.
99
Контрольная работа № 7 по теме «Алгебраические дроби»
Параллельные прямые, 13 часов
100
Признаки параллельности двух прямых.
101
Признаки параллельности двух прямых.
102
Практические способы построения параллельных прямых
103
Решение задач по теме «Признаки параллельности прямых»
104
Аксиома параллельных прямых.
105
Свойства параллельных прямых
106
Свойства параллельных прямых
107
Решение задач по теме «Параллельные прямые»
108
Решение задач по теме «Параллельные прямые»
109
Решение задач.
110
Решение задач.
111
Решение задач. Подготовка к контрольной работе.
112
Контрольная работа № 8. По теме «Параллельные прямые»
Линейная функция и ее график, 10 часов
113
Прямоугольная система координат на плоскости
114
Прямоугольная система координат на плоскости
115
Функции
116
Функции
117
Функции
118
Функция y = kx и ее график
119
Функция y = kx и ее график
120
Функция y = kx и ее график
121
Линейная функция и ее график
122
Контрольная работа № 9 по теме «Линейная функция и её график.»
Система двух уравнений с двумя неизвестными, 11 часов
123
Системы уравнений
124
Системы уравнений
125
Способ подстановки
126
Способ подстановки
127
Способ сложения
128
Способ сложения
129
Графический способ решения систем уравнений
130
Графический способ решения систем уравнений
131
Решение задач с помощью уравнений
132
Обобщение, систематизация и коррекция знаний.
133
Контрольная работа № 10 по теме «Система двух уравнений с двумя неизвестными»
Глава 4. Соотношение между сторонами и углами треугольника, 18 часов
134
Сумма углов треугольника.
135
Сумма углов треугольника. Решение задач.
136
Соотношение между сторонами и углами треугольника.
137
Соотношение между сторонами и углами треугольника.
138
Неравенство треугольника
139
Решение задач. Подготовка к контрольной работе
140
Контрольная работа № 11 по теме: «Соотношение между сторонами и углами треугольника»
141
Прямоугольные треугольники и их свойства.
142
Решение задач на применение свойств прямоугольных треугольников
143
Признаки равенства прямоугольных треугольников.
144
Признаки равенства прямоугольных треугольников.
145
Прямоугольные треугольники. Решение задач.
146
Расстояние от точки до прямой. Расстояние между параллельными прямыми.
147
Построение треугольника по трем элементам.
148
Решение задач на построение.
149
Решение задач на построение.
150
Решение задач. Подготовка к контрольной работе.
151
Контрольная работа № 12. По теме: «Соотношение между сторонами и углами треугольника»
Введение в комбинаторику,7 часов
152
Исторические комбинаторные задачи
153
Различные комбинации из трех элементов
154
Различные комбинации из трех элементов
155
Таблица вариантов и правило произведения
156
Таблица вариантов и правило произведения
157
Подсчет вариантов с помощью графов
158
Подсчет вариантов с помощью графов
Повторение, 12часов
Литература
-
Ш.А. Алимов., Ю.М. Колягин., Ю.В Сидоров., Н.Е Федорова., М.И Шабунин. Алгебра: Учеб. для 7 кл. - М.: Просвещение, 2009.
-
Л. С Атанасян., В. Ф Бутузов., С. Б Кадомцев., Э. Г Позняк., И. И Юдина. Геометрия 7-9. - М.: Просвещение, 2008.
-
Б. Г Зив., В. М Мейлер., Дидактические материалы по геометрии за 7 класс. - М.: Просвещение,
-
Е.Г Лебедева.Алгебра.7 класс. Поурочные планы . «Учитель»
5 . Н.Ф. Гаврилова . Поурочные разработки по геометрии за 7 класс -«М.Вако»2006.
-
Е.В. Лебедева. Поурочные планы по учебнику Ш.А. Алимова 8 класс- «Волгоград, учитель» 2011.
-
И.В. Фотина., Коллективный способ изучения математики; 2009.
-
В.И. Жохов., Дидактические материалы за 7 класс; 2006 год- М.: Просвещение.
-
М.Н. Ляшова., Открытые уроки математики 5-11 класс - «Волгоград учитель».
-
М.Ю. Бессонова., Поурочные планирования по алгебре к учебнику А.Ш. Алимова, алгебра 7 класс-Издательство «Экзамен» 2008.
График проведения контрольных работ.
-
№
п/п
Тема
Ориент.
сроки.
1.
Контрольная работа № 1 по теме «Алгебраические выражения»
2.
Контрольная работа № 2. По теме «Начальные геометрические сведения»
3.
Контрольная работа № 3 по теме «Уравнения с одним неизвестным»
4.
Контрольная работа № 4 по теме: «Треугольники»
5.
Контрольная работа № 5 по теме «Одночлены и многочлены»
6.
Контрольная работа № 6 по теме «Разложение многочленов на множители»
7.
Контрольная работа № 7 по теме «Алгебраические дроби»
8.
Контрольная работа № 8. По теме «Параллельные прямые»
9.
Контрольная работа № 9 по теме «Линейная функция и её график.»
10.
Контрольная работа № 10 по теме «Система двух уравнений с двумя неизвестными»
11.
Контрольная работа № 11 по теме: «Соотношение между сторонами и углами треугольника»
12.
Контрольная работа № 12. По теме: «Соотношение между сторонами и углами треугольника»
Критерии и нормы оценки ЗУН, обучающихся применительно к различным формам контроля знаний по математике
-
Критерии.
1.1 Основой для определения уровня знаний являются критерии оценивания - полнота знаний, их обобщенность и системность:
-
полнота и правильность - это правильный, полный ответ;
-
правильный, но неполный или неточный ответ;
-
неправильный ответ;
-
нет ответа.
1.2 При выставление отметок необходимо учитывать классификацию ошибок и их количество:
-
грубые ошибки;
-
однотипные ошибки;
-
негрубые ошибки;
-
недочеты.
2 Шкала отметок
При оценке знаний и умений используется 5 - бальная система оценок, в соответствии с требованиями устава школы.
2.1 Оценка письменных контрольных работ обучающихся по математике.
Работа оценивается отметкой «5», если:
- работа выполнена полностью (100%);
- в логических рассуждениях и обосновании решения нет пробелов и ошибок;
- в решении нет математических ошибок (возможна одна неточность, описка, которая не является следствием незнания или непонимания учебного материала).
Отметка «4» ставится в следующих случаях:
- работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);
- допущены одна ошибка или есть два - три недочёта в выкладках, рисунках, чертежах или графиках (если эти виды работ не являлись специальным объектом проверки);
- работа соответствует 70-90%.
Отметка «3» ставится, если:
- допущено более одной ошибки или более двух - трех недочетов в выкладках, чертежах или графиках, но обучающийся обладает обязательными умениями по проверяемой теме или выполнено 45-69% работы.
Отметка «2» ставится, если:
- допущены существенные ошибки, показавшие, что обучающийся не обладает обязательными умениями по данной теме в полной мере.
- работа показала полное отсутствие у обучающегося обязательных знаний и умений по проверяемой теме или значительная часть работы выполнена не самостоятельно.
Учитель может повысить отметку за оригинальный ответ на вопрос или оригинальное решение задачи, которые свидетельствуют о высоком математическом развитии обучающегося; за решение более сложной задачи или ответ на более сложный вопрос, предложенные обучающемуся дополнительно после выполнения им каких-либо других заданий.
2.2 Оценка устных ответов обучающихся по математике.
Ответ оценивается отметкой «5», если ученик:
- полно раскрыл содержание материала в объеме, предусмотренном программой и учебником;
- изложил материал грамотным языком, точно используя математическую терминологию и символику, в определенной логической последовательности;
- правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;
- показал умение иллюстрировать теорию конкретными примерами, применять ее в новой ситуации при выполнении практического задания;
- продемонстрировал знание теории ранее изученных сопутствующих тем, сформированность и устойчивость используемых при ответе умений и навыков;
- отвечал самостоятельно, без наводящих вопросов учителя;
- возможны одна - две неточности при освещение второстепенных вопросов или в выкладках, которые ученик легко исправил после замечания учителя.
Ответ оценивается отметкой «4», если удовлетворяет в основном требованиям на оценку «5», но при этом имеет один из недостатков:
- в изложении допущены небольшие пробелы, не исказившее математическое содержание ответа;
- допущены один - два недочета при освещении основного содержания ответа, исправленные после замечания учителя;
- допущены ошибка или более двух недочетов при освещении второстепенных вопросов или в выкладках, легко исправленные после замечания учителя.
Отметка «3» ставится в следующих случаях:
- неполно раскрыто содержание материала (содержание изложено фрагментарно, не всегда последовательно), но показано общее понимание вопроса и продемонстрированы умения, достаточные для усвоения программного материала (определены «Требованиями к математической подготовке учащихся» в настоящей программе по математике);
- имелись затруднения или допущены ошибки в определении математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов учителя;
- ученик не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме;
- при достаточном знании теоретического материала выявлена недостаточная сформированность основных умений и навыков.
Отметка «2» ставится в следующих случаях:
- не раскрыто основное содержание учебного материала;
- обнаружено незнание учеником большей или наиболее важной части учебного материала;
- допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов учителя.
- ученик обнаружил полное незнание и непонимание изучаемого учебного материала или не смог ответить ни на один из поставленных вопросов по изученному материалу.
2.3. Общая классификация ошибок.
при оценке знаний, умений и навыков учащихся следует учитывать все ошибки (грубые и негрубые) и недочёты.
Грубыми считаются ошибки:
- незнание определения основных понятий, законов, правил, основных положений теории, незнание формул, общепринятых символов обозначений величин, единиц их измерения;
- незнание наименований единиц измерения;
- неумение выделить в ответе главное;
- неумение применять знания, алгоритмы для решения задач;
- неумение делать выводы и обобщения;
- неумение читать и строить графики;
- неумение пользоваться первоисточниками, учебником и справочниками;
потеря корня или сохранение постороннего корня;
- отбрасывание без объяснений одного из них;
- равнозначные им ошибки;
- вычислительные ошибки, если они не являются опиской;
- логические ошибки.
К негрубым ошибкам следует отнести:
- неточность формулировок, определений, понятий, теорий, вызванная неполнотой охвата основных признаков определяемого понятия или заменой одного - двух из этих признаков второстепенными;
- неточность графика;
- нерациональный метод решения задачи или недостаточно продуманный план ответа (нарушение логики, подмена отдельных основных вопросов второстепенными);
- нерациональные методы работы со справочной и другой литературой;
- неумение решать задачи, выполнять задания в общем виде.
Недочетами являются:
- нерациональные приемы вычислений и преобразований;
- небрежное выполнение записей, чертежей, схем, графиков.
3 Формы и сроки контроля.
-
Формы контроля: текущий контроль, текущий письменный контроль .Текущий и текущий письменный контроль успеваемости осуществляется учителями на протяжении всего учебного года и осуществляет проверку знаний учащихся в соответствии с учебной программой.
-
Учитель обязан ознакомить с системой текущего контроля учащихся на начало учебного года.
-
Учитель обязан своевременно и тактично довести до учащихся отметку текущего и текущего письменного контроля, обосновав ее в присутствии всего класса и выставить оценку в классный журнал.
-
Четвертные и полугодовые отметки в 5, 6 классах по математике, в 7 классе по алгебре и геометрии, 8, 9, 10, 11 классах по геометрии выставляется исходя из текущих оценок и контрольных работ.
-
Четвертные и полугодовые отметки в 8, 9 классах по алгебре и 10, 11 классах по алгебре и началам анализа выставляется на основании только текущих письменных работ (текущие отметки не ставятся).
4 Количество отметок.
4.1 Количество отметок для выставления четвертных в 8, 9 классах по алгебре должно быть не менее пяти. Количество отметок, для выставления итоговой отметки за полугодие в 10, 11 классах по алгебре и началам анализа, должно быть не менее семи.
4.2. Количество отметок за урок:
- математика 5-6 класс - не менее пяти отметок (при объяснении нового материала отметок может и не быть);
- алгебра 7 класс - не менее четырех отметок (при объяснении нового материала отметок может и не быть);
- геометрия 7-11 классы - не менее четырех отметок (при объяснении нового материала отметок может и не быть).