Методическая разработка

«Тематические тесты по математике для подготовки к ЕГЭ»

Подготовила учитель математики Галиуллина Р.Ф.

Содержание.

1. Арифметические вычисления, действия со степенями и радикалами. Стр.3

2. Тождественные преобразования алгебраических выражений. Стр. 5

3. Квадратные уравнения. Приложения теоремы Виета. Стр.7

4. Исследования квадратного трехчле хчлена. Стр.9

5. Арифметическая и геометрическая прогрессии. Стр.11

6. Рациональные уравнения и системы. Стр.13

7. Рациональные неравенства. Стр.15

8. Уравнения и неравенства, содержащие переменную под знаком модуля. Стр.7

9. Иррациональные уравнения и неравенства.Стр.9

10. Тригонометрические преобразования и вычисления. Стр.21

11. Действия с обратными тригонометрическими функциями. Стр.23

12. Тригонометрические уравнения. Стр.25

13. Тождественные преобразования и вычисления показательных и логарифмических выражений. Стр27.

14. Показательные и логарифмические уравнения. Стр29

15. Показательные и логарифмические неравенства. Стр31

16. Уравнение касательной к графику функции. Стр.33

17. Исследование функции с помощью производной. Стр.35

18. Векторы, их геометрические приложения. Метод координат. Стр.37

19. Задачи по планиметрии. Стр.39

20. Задачи по стереометрии. Стр.41

Ответы .Стр.43-44.

Предисловие.

Данная методическая разработка содержит комплект тематических тестов для подготовки к ЕГЭ. Каждый тест содержит 20 задач, среди которых есть задания как части В, так и части С . Ко всем тестам даны ответы, которые представлены в конце в таблице.

Комплект тематических тестов дает возможность готовиться к ЕГЭ по математике, выбрав задачи по той теме, которая вызывает наибольшую трудность.

Его можно использовать как для самостоятельной подготовки к ЕГЭ , так и на учебных занятиях итогового повторения.

1. Арифметические вычисления, действия со степенями и радикалами.

зада

ния

Условие задания

Варианты ответов

1

Значения скольких из приведенных ниже выражений являются рациональными числами?

; ; ; ; ;

1) 0 2) 4 3) 3 4) 2 5) 1

2

Сколько процентов числа 4 составляет разность между ним и 3 % числа 20?

1) 75 2) 80 3) 85 4) 90 5) 95

3

В разложении числа 12600 входят следующие различные простые множители

1) 1,2,3,5,7 2) 8,9,25,7 3) 2,3,25,7 4) 2,3,5,7 5) 2,3,5,13

4

Вычислить .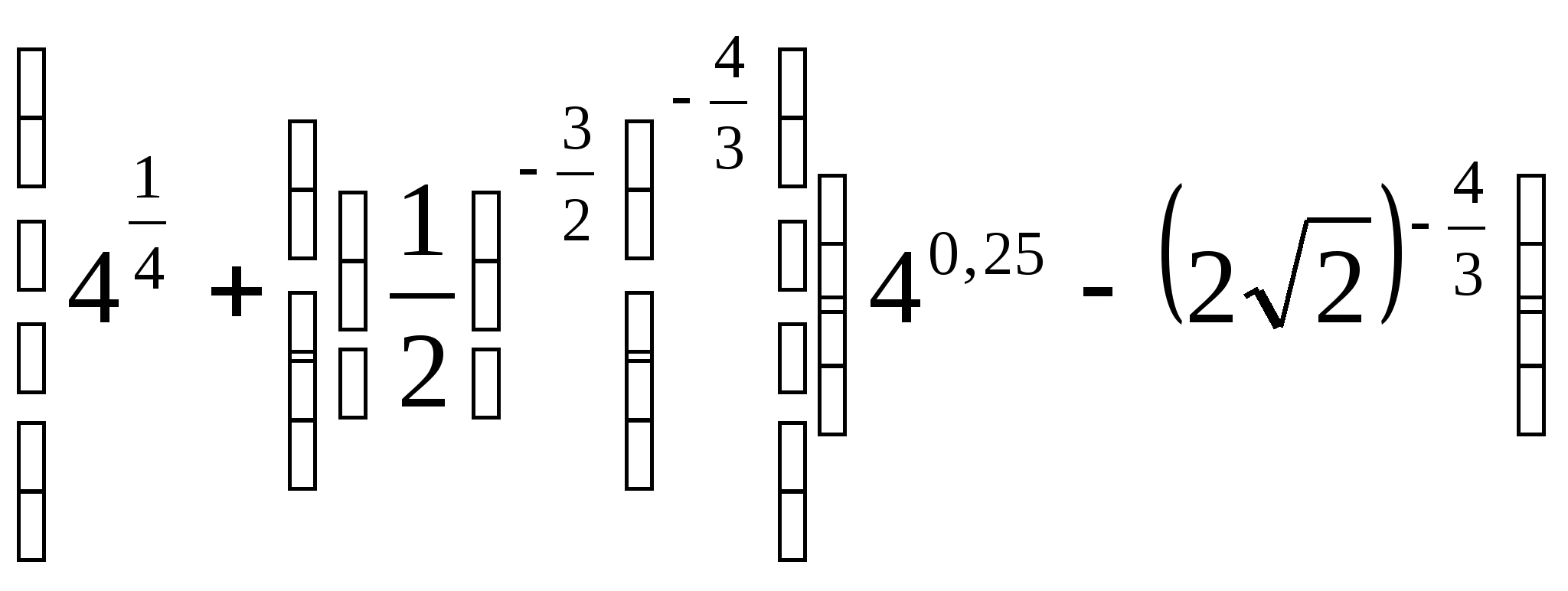

1) 2) 3) 4) 5)

5

Найти сумму остатков, получающихся при делении числа 2736455478346791 на 2,4,5,9,10,25.

1) 22 2) 19 3) 26 4) 21 5) 35

6

Число увеличили на 15 %, получили 109,25. Отсюда следует, что значение равно

1) 93,05 2) 95 3) 96 4) 93,08 5) 92,86

7

Значение выражения после упрощения равно

1) 2) 3) 4) 5)

8

Пусть сумма первых трех членов пропорции равна 59. Тогда, если второй член составляет , а третий первого члена, то четвертый член пропорции равен

1) 2) 3) 4) 5)

9

Среднее арифметическое чисел и равно

1) 2) 3) 4) 5)

10

Даны числа 600 и 1260. Частное от деления наименьшего кратного этих чисел на их наибольший общий делитель равно

1) 42 2) 210 3) 30 4) 1050 5) 420

11

Числители трех дробей пропорциональны числам 1, 2, 3, а знаменатели пропорциональны соответственно числам 1, 5, 4. Тогда, если среднее арифметическое этих дробей равно , то наименьшая из дробей есть

1) 2) 3) 4) 5)

12

Число, % которого составляют 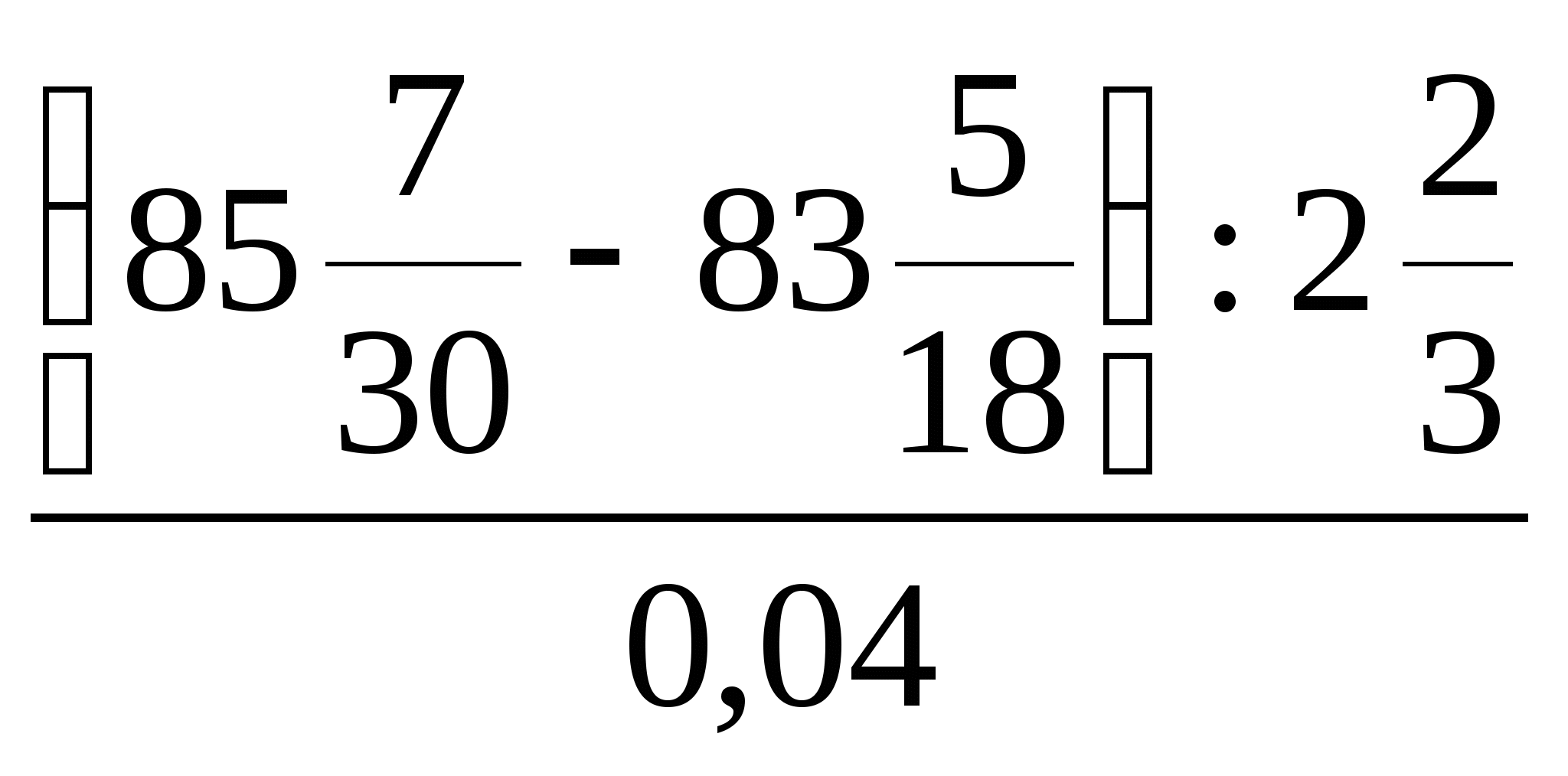, равно

1) 0,672 2) 400 3) 672 4) 500 5) 472

13

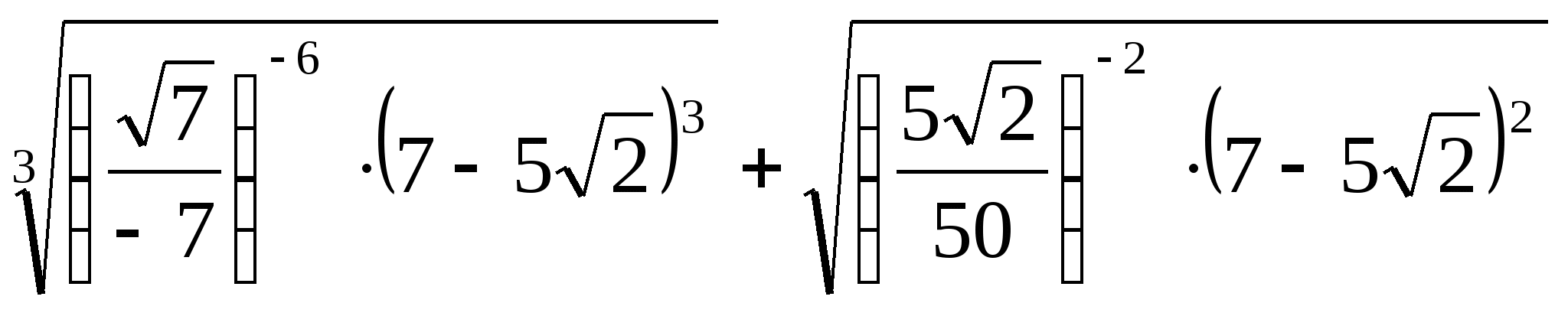. Результат вычислений равен

1) -1 2) 3) 1

4) 5) 0,005

14

Результат вычислений выражения 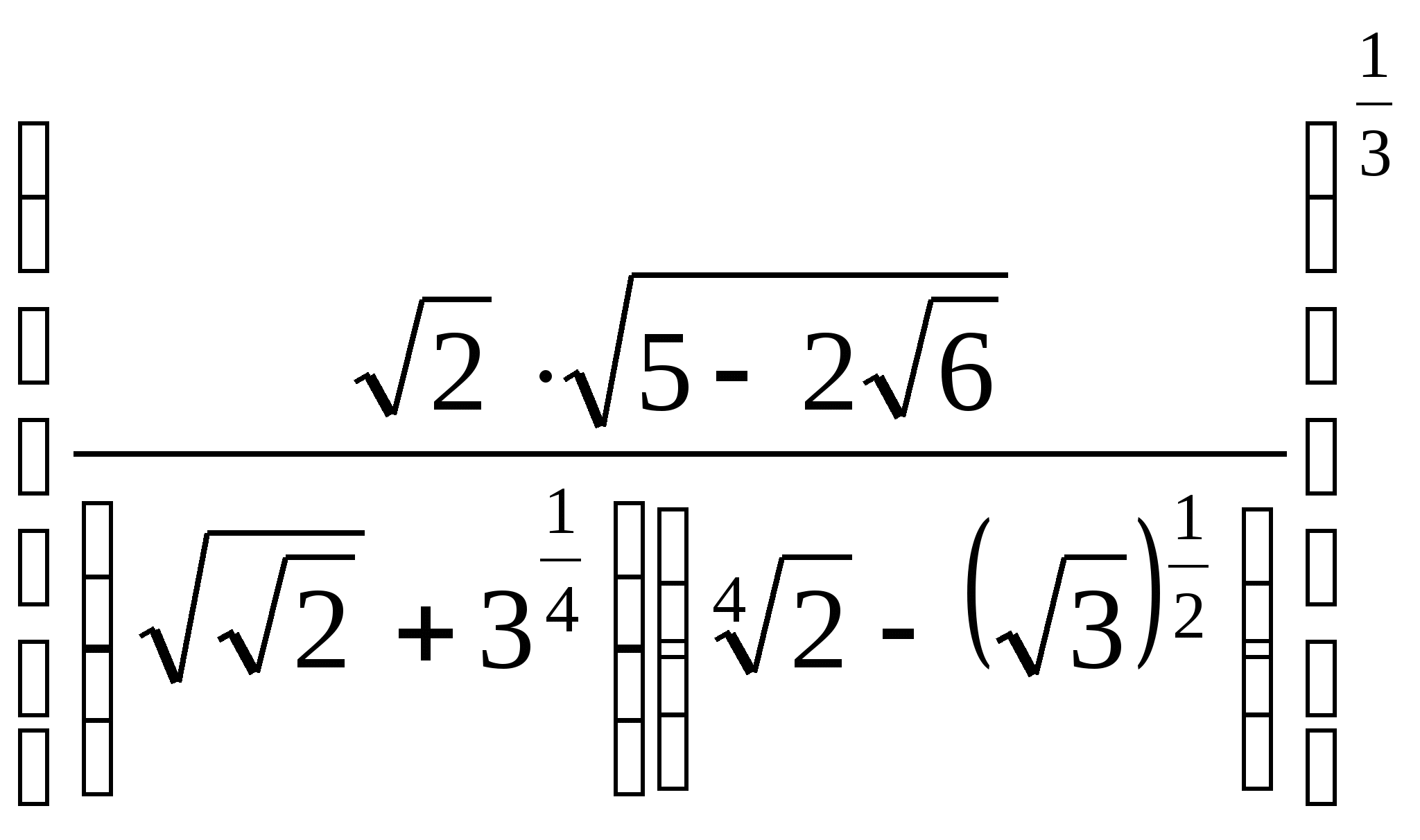равен

1) 2) 3) 1,12 4) 5)

15

Если 20 % числа равны , то это число равно

1) 15 2) 20 3) 25 4) 30 5) 35

16

Если 40 % числа равны , то это число равно

1) 2) 3) 4) 5)

17

Если , то равно

1) 2) 1 3) 4) 2 5)

18

Значение выражения равно

1) 2) 3) 1 4) 5)

19

Значение выражения 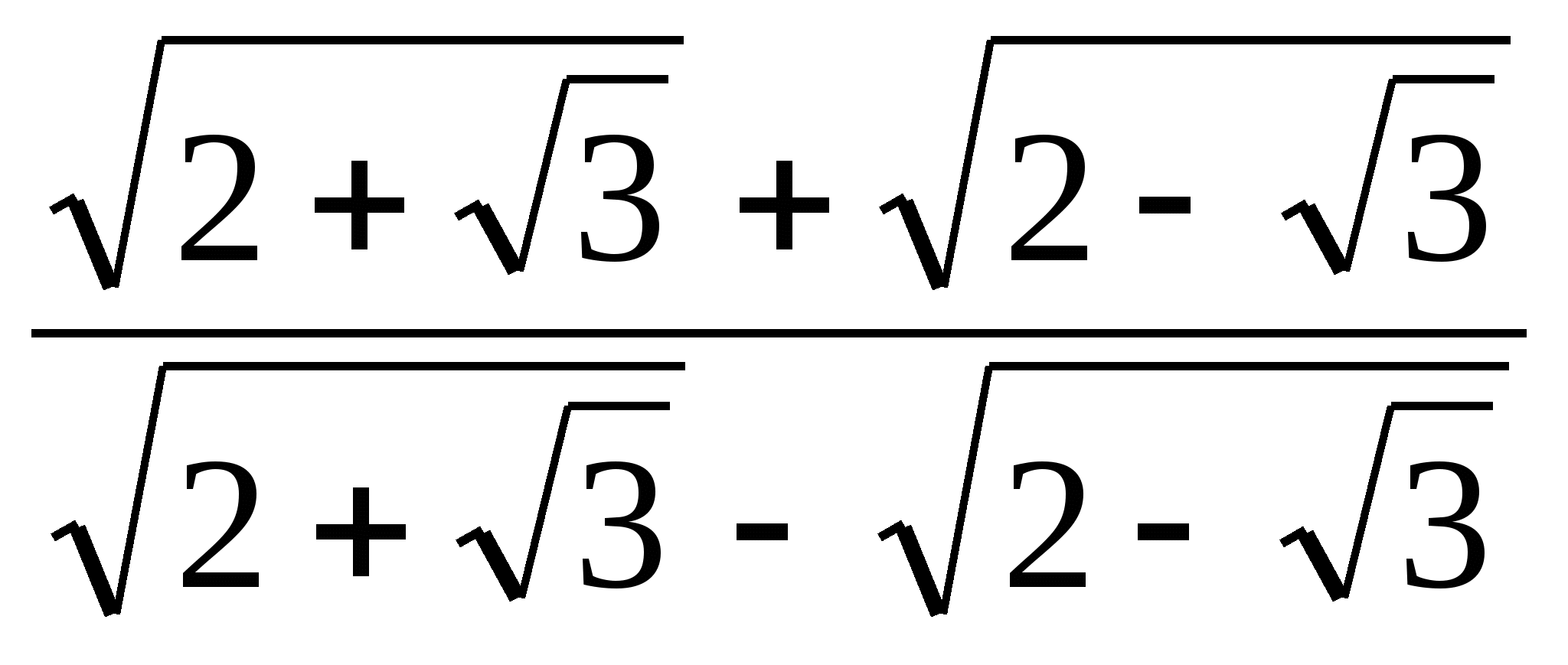равно

1) 1,5 2) 3) 4) 5)

20

Если и , то выражение равно

1) 2) 3) 4) 5) другому числу

2. Тождественные преобразования алгебраических выражений.

зада

ния

Условие задания

Варианты ответов

1

Сократить дробь .

1) 2) 3) 4) 5)

2

Упростить .

1) 2)

3) 4) 5)

3

Результат сокращения дроби имеет вид

1) 2) 3) 4) 5)

4

Результат сокращения дроби имеет вид

1) 2)

3) 4) 5)

5

Выражение после упрощения имеет вид

1) 2) 3) 4) 5)

6

Выражение после упрощения имеет вид

1) 2) 3) 4) 5)

7

Выражение после упрощения имеет вид

1) 2) 3) 4) 5)

8

Выражение после упрощения имеет вид

1) 2) 3) 4) 5)

9

Результат упрощения выражения 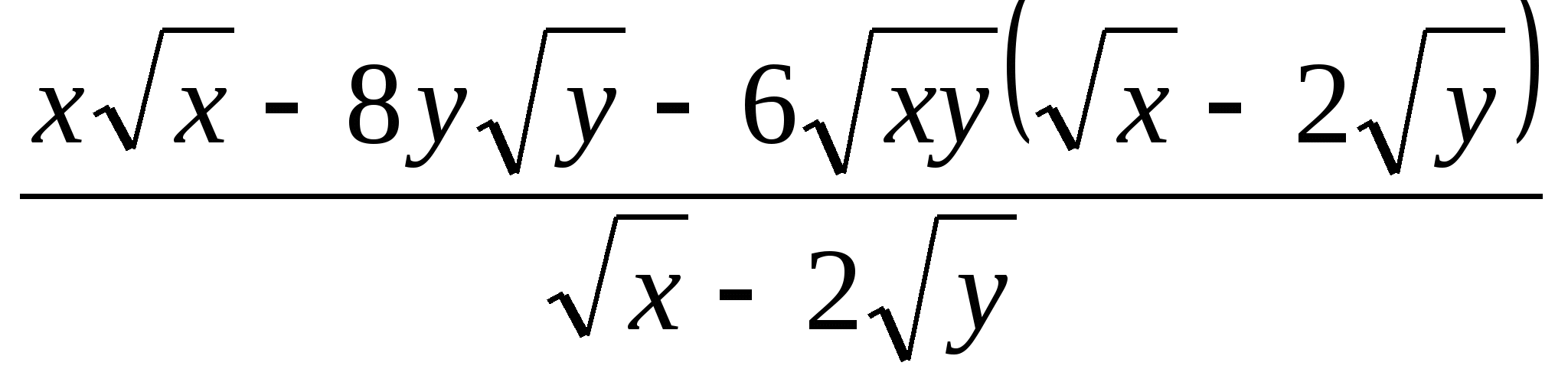имеет вид

1) 2) 3) 4) 5)

10

Результат упрощения выражения 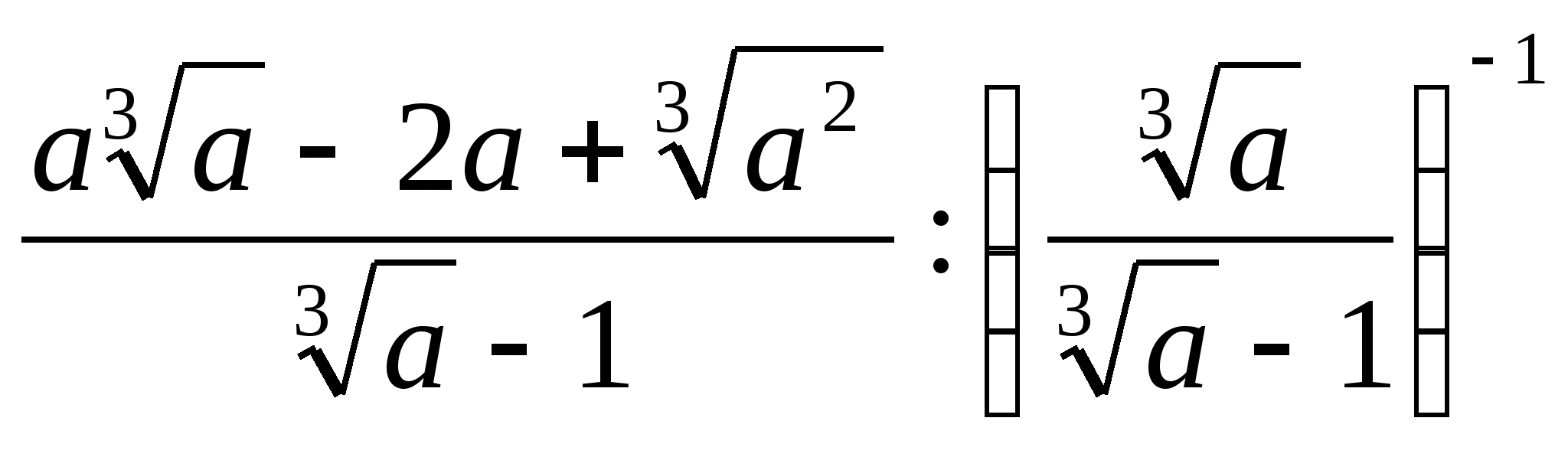имеет вид

1) 2) 3) 4) 5)

Выражение

в результате упрощения имеет вид

1) 2) 3) 4) 5)

16

Выражение

в результате упрощения имеет вид

1) 2) 3) 4) 5)

17

Выражение

в результате упрощения имеет вид

1) 2) 3) 4) 5)

18

Выражение

в результате упрощения имеет вид

1) 2)

3) 4)

5)

19

Выражение равно

1) 2)

3) 4) 5)

20

Значение выражения 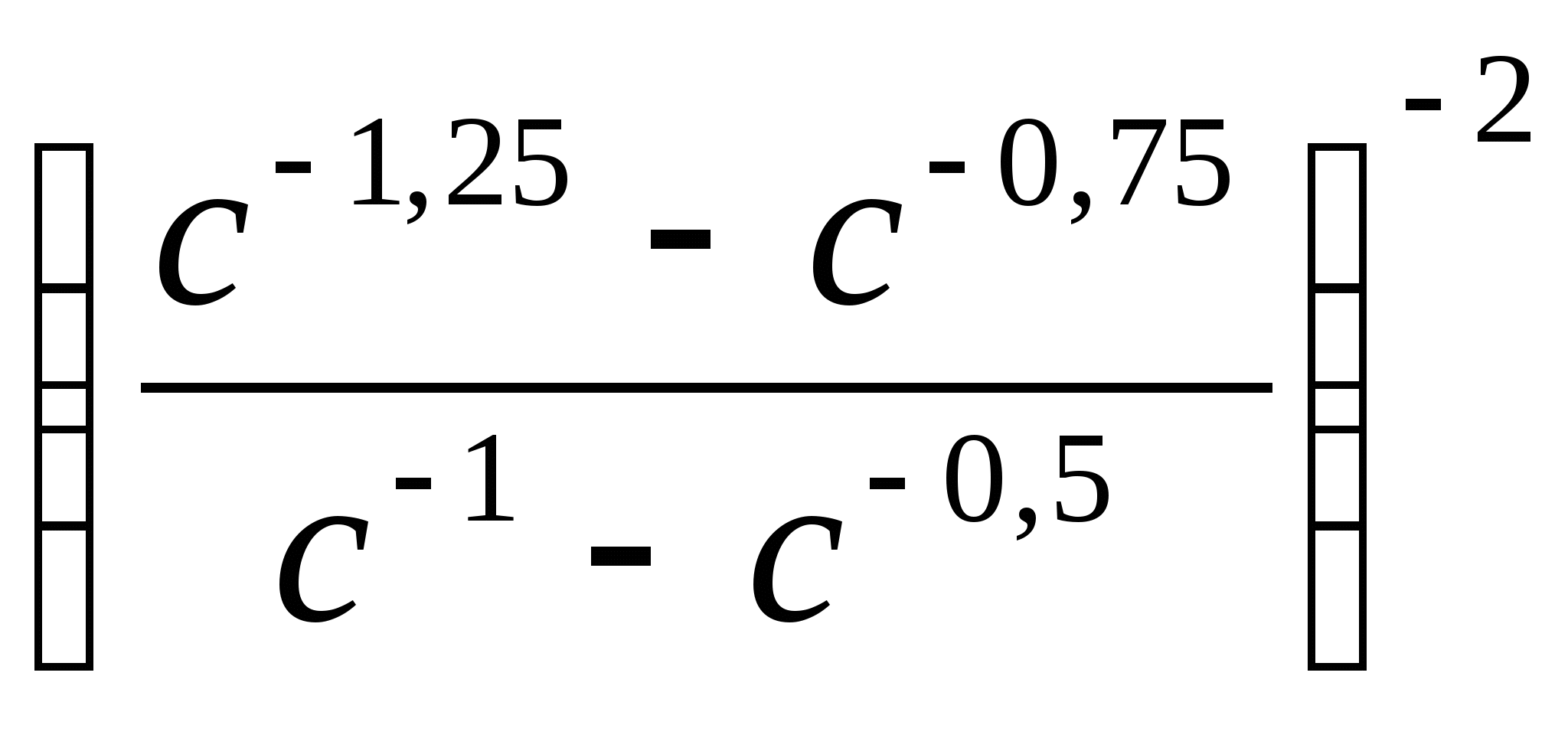при равно

1) 2) 3) 4) 5) 40

3. Квадратные уравнения. Приложения теоремы Виета.

зада

ния

Условие задания

Варианты ответов

1

Дано уравнение , и - его корни. Найти , если , а корни положительны.

1) -5 2) -3 3) -4 4) -6 5) -9

2

Составить квадратное уравнение, корни которого равны утроенным корням уравнения .

1)

2)

3)

4)

5)

3

Квадратное уравнение с рациональными коэффициентами, один из корней которого равен , имеет вид

1)

2)

3)

4)

5)

4

Сумма кубов корней уравнения равна

1) 2) 3) 4) 5)

5

Корни уравнения удовлетворяют условию , если равно

1) -55 2) 39 3) 60 4) -45 5) 45

6

В уравнении сумма квадратов корней равна 25, если равно

1) 36 2) -36 3) 42 4) -42 5) 24

7

Оба корня уравнения положительны, если удовлетворяет условию

1) 2)

3) 4) 5)

8

Оба корня уравнения отрицательны, если

1) 2)

3) 4)

5)

9

Сумма корней уравнения равна

1) 4 2) -2 3) 5 4) 3 5) -5

10

Корень уравнения принадлежит промежутку

1) 2) 3) 4) 5)

11

Найдите наименьшее значение , при котором уравнение имеет один корень.

12

Найдите наибольшее целое значение параметра , при котором уравнение имеет два различных действительных корня.

4. Исследования квадратного трехчлена.

зада

ния

Условие задания

Варианты ответов

1

Парабола расположена выше оси , если

1) 2) 3) 4) 5)

2

Квадратный трехчлен принимает только отрицательные значения, если принадлежит множеству

1) 2) 3) 4)

5)

3

Парабола не имеет общих точек с осью , если

1) 2) 3) 4) 5)

4

Парабола пересекает ось в двух точках, лежащих в правой полуплоскости, если принадлежит промежутку

1) 2) 3) 4) 5)

5

Корни квадратного трехчлена отрицательны, если принадлежит промежутку

1) 2) 3) 4) 5)

6

Если точка с координатами принадлежит параболе с вершиной в точке , то уравнение параболы имеет вид

1)

2)

3)

4)

5)

7

График квадратного трехчлена имеет общие точки с положительной полуосью , если принадлежит промежутку

1) 2) 3) 4) 5)

8

Точка принадлежит параболе с вершиной , если уравнение параболы имеет вид

1)

2)

3)

4)

5)

9

Квадратный трехчлен можно представить в виде квадрата двучлена, если принадлежит множеству

1) 2) 3) 4) 5)

10

График функции , убывающей на промежутке , пересекает ось ординат в точке 6, если равно

1) -2 2) 3 3) -3 4) 0 5) 2

11

Количество целых значений параметра , при которых абсцисса и ордината вершины параболы положительны, равно

1) 0 2) 1 3) 2 4) 3 5) 4

12

Количество целых значений параметра , при которых абсцисса вершины параболы отрицательна, а ордината положительна, равно

1) 7 2) 6 3) 4 4) 8 5) 5

13

Количество целых значений параметра , при которых абсцисса и ордината вершины параболы отрицательны, равно

1) 1 2) 5 3) 0 4) 2 5) 4

14

Найдите произведение коэффициентов трехчлена , зная, что он принимает наибольшее значение, равное 5, в точке , а его график пересекает ось в точке с ординатой, равной -4.

15

Найдите сумму коэффициентов трехчлена , зная, что он обращается в нуль при и что его наименьшее значение равно -8 при .

16

Найдите наибольшее значение функции , если ее график проходит через точки и .

17

Задайте формулой квадратичную функцию, если ее график проходит через точки и и функция принимает значение -4 в единственной точке. В ответ запишите наибольшую сумму коэффициентов.

18

Задайте формулой квадратичную функцию, если ее значения при и при совпадают, ее наибольшее значение равно 3, а график содержит точку . В ответ запишите сумму коэффициентов.

19

Сумма коэффициентов квадратного трехчлена равна 2. Найдите произведение его корней, если координаты вершины графика соответствующей ему квадратичной функции .

20

Найдите отношение абсциссы и ординаты вершины графика квадратичной функции, если сумма корней соответствующего ей квадратного трехчлена равна 5, сумма квадратов корней равна 13. а сумма коэффициентов трехчлена равна -2.

5. Арифметическая и геометрическая прогрессии.

зада

ния

Условие задания

Варианты ответов

1

Найти сумму шести первых членов геометрической прогрессии, у которой четвертый член равен -16, а первый член равен 2.

1) -40 2) -42 3) -44 4) -46 5) -4

2

Сумма первого и третьего членов арифметической прогрессии равна 12, а ее четвертый член равен 12. Найти сумму первых пятнадцати членов прогрессии.

1) 360 2) 375 3) 390 4) 405 5) 420

3

Произведение первого и четвертого членов возрастающей геометрической прогрессии с положительными членами равно 27, а сумма второго и третьего ее членов равна 12. Найти сумму второго и пятого членов прогрессии.

1) 82 2) 83 3) 84 4) 85 5) 86

4

Третий член арифметической прогрессии равен 8, а ее седьмой член равен 16. Найти сумму второго и шестого членов прогрессии.

1) 19 2) 20 3) 21 4) 22 5) 23

5

Если первый член геометрической прогрессии равен 4, а четвертый член равен -32, то сумма первых шести ее членов равна

1) 84 2) -84 3) -82 4) -6 5) 6

6

Пусть сумма шести первых членов геометрической прогрессии равна 910, а знаменатель равен 3. Тогда сумма первого и пятого ее членов равна

1) 305 2) 410 3) 205 4) 284 5) 192

7

В геометрической прогрессии, все члены которой положительны, первый член равен 243, а сумма первых трех членов равна 351. Тогда пятый член этой прогрессии равен

1) 1 2) 3 3) 9 4) 27 5) 81

8

В арифметической прогрессии сумма первых четырнадцати членов равна 112, а пятый член равен 13. Тогда сумма второго и шестого членов этой прогрессии равна

1) 30 2) 36 3) 42 4) 48 5) 54

9

В арифметической прогрессии, пятый член которой равен 18, сумма первых девяти членов равна

1) 138 2) 150 3) 162 4) 174 5) 186

10

В геометрической прогрессии, все члены которой отрицательные, сумма пятого и шестого членов равна -648, а четвертый член этой прогрессии равен -54. Тогда сумма первых четырех членов этой прогрессии равна

1) -50 2) -60 3) -70 4) -80 5) -90

11

Если в арифметической прогрессии первый и девятый члены соответственно равны -6 и 10, то сумма первых двенадцати ее членов равна

1) 20 2) -10 3) 80 4) 60 5) 36

6. Рациональные уравнения и системы.

зада

ния

Условие задания

Варианты ответов

1

Если система уравнений 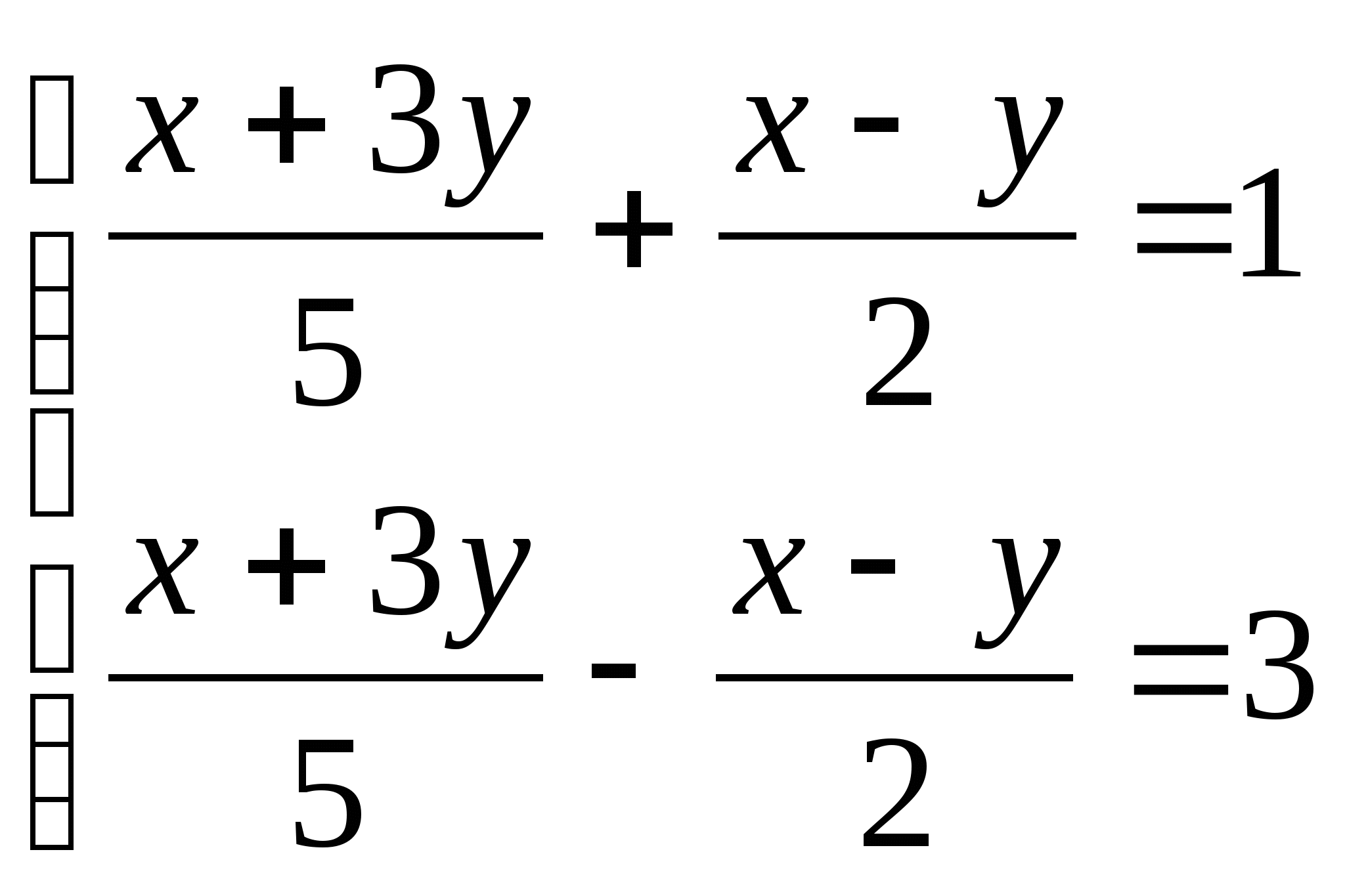имеет решение , то значение выражения равно

1) 4 2) -8 3) 8 4) 6 5) -4

2

Система уравнений имеет бесчисленное множество решений при , равном

1) 2 2) 3 3) 4 4) 6 5) 8

3

Если прямая проходит через точку пересечения прямых и , то значение равно

1) -3 2) -1 3) 4) 3 5) 5

4

Среднее арифметическое всех действительных корней уравнения равно

1) -2 2) 1 3) -1 4) 5)

5

Среднее арифметическое всех действительных корней уравнения равно

1) 2 2) 0 3) -1 4) 1 5)

6

Среднее арифметическое всех действительных корней уравнения равно

1) 2) 3) 0 4) 5)

7

Произведение корней уравнения равно

1) 2) -2 3) 8 4) -8 5) 10

8

Произведение корней уравнения равно

1) -6 2) 6 3) 4 4) -4 5) 1

9

Корень уравнения принадлежит промежутку

1) 2) 3) 4) 5)

10

Произведение корней уравнения равно

1) -1,8 2) 1,6 3) -1,2 4) 1,8 5) 2

11

Уравнение имеет два различных действительных корня, если принадлежит множеству

1) 2) 3) 4) 5)

12

Найти все значения параметра , при которых система уравнений 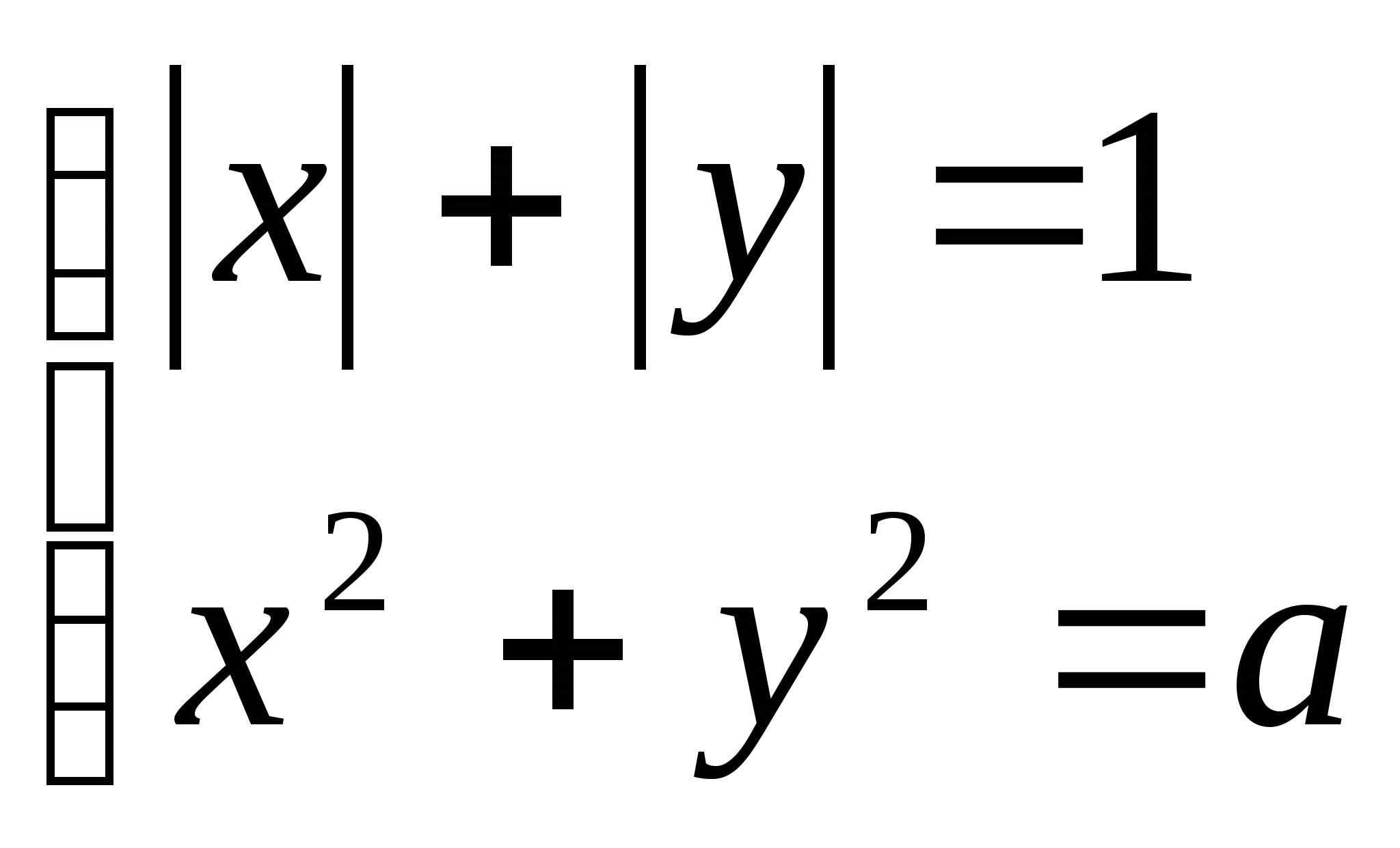имеет ровно четыре решения.

1) или 1 2) или 1 3) 4) 1 5)

1) 2) 3) 4)

5) правильного ответа нет

15

Найти наибольшее значение , при котором любое решение системы удовлетворяет неравенству .

16

Найти произведение всех значений , при которых система 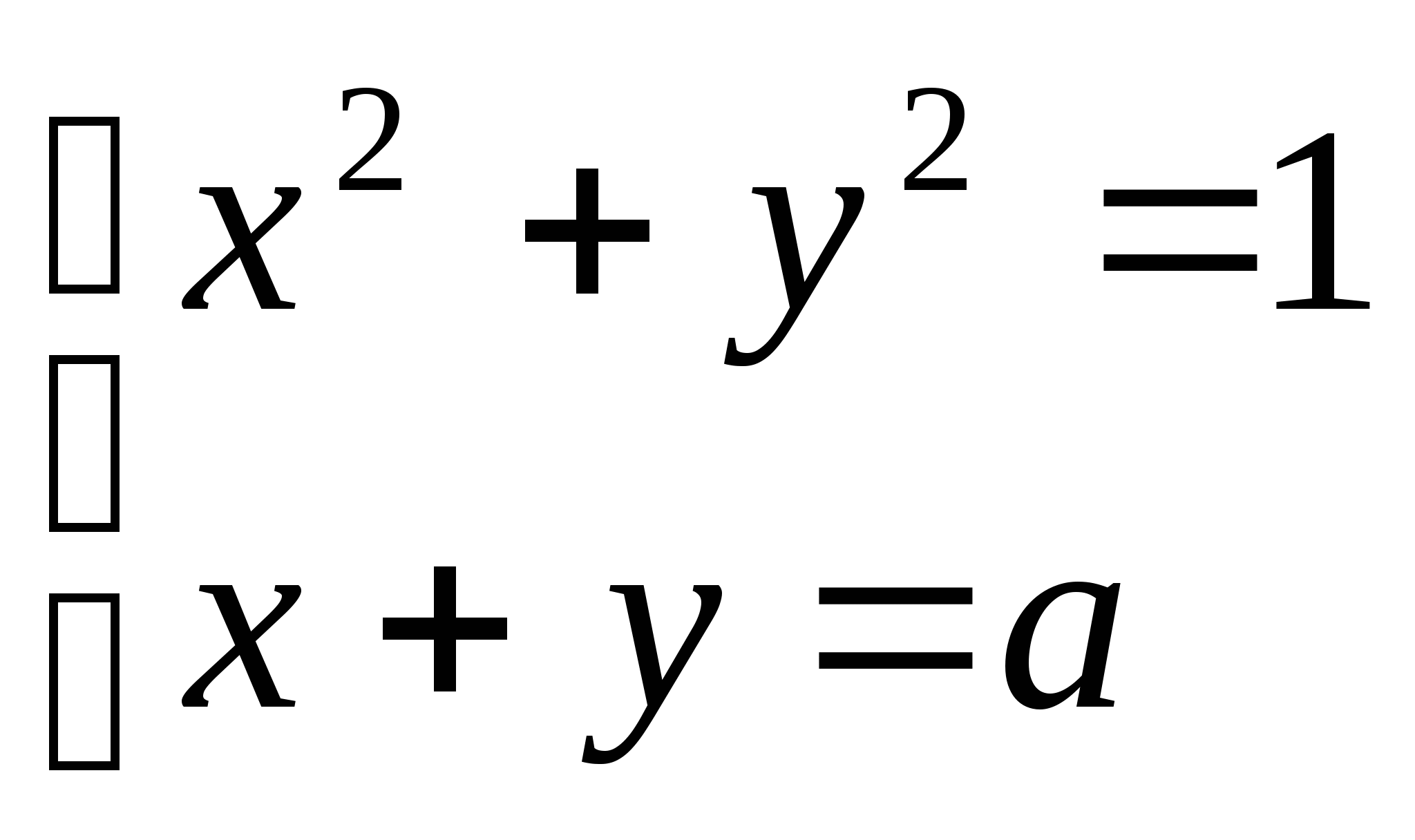имеет единственное решение.

17

Если - все целочисленные решения системы , то значение всех равно…

18

Найти наименьшее значение выражения при условии .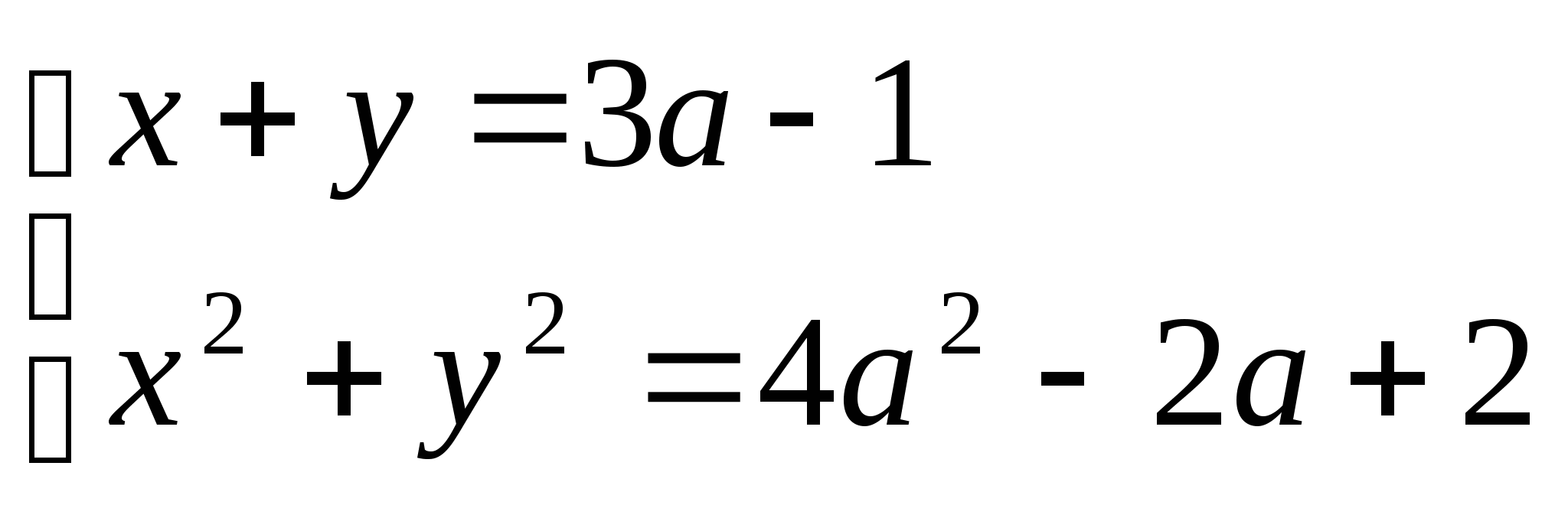

19

Найти , где - наибольшее значение , при котором уравнение имеет единственное решение.

20

Найти все значения , при которых уравнение имеет два различных корня. В ответ записать сумму длин конечных промежутков.

7. Рациональные неравенства.

зада

ния

Условие задания

Варианты ответов

1

Наибольшее решение неравенства равно

1) -1 2) -3 3) 1 4) 3 5) 0

2

Если - наибольшее из решений неравенства , то значение выражения равно

1) 2 2) 3) 3 4) 5 5)

3

Решение неравенства имеет вид

1)

2)

3)

4) 5)

4

Решение неравенства имеет вид

1)

2) 3) 4)

5)

5

Решение неравенства имеет вид

1)

2) 3) 4) 5)

6

Решение неравенства имеет вид

1) 2) 3) 4) 5)

7

Решение неравенства имеет вид

1) 2) 3) 4) 5)

1) 2)

3) 4)

5)

9

Среднее арифметическое всех целых решений неравенства равно

1) 5 2) 3 3) 6 4) 4 5) 7

10

Выберите промежуток, не содержащий ни одного решения неравенства .

1) 2) 3) 4) 5) среди предложенных правильного ответа нет

11

Число целых решений неравенства на промежутке равно

1) 3 2) 5 3) 3 4) 4 5) 7

12

Наибольшее целое решение, удовлетворяющее неравенству , равно

1) -2 2) -1 3) 2 4) 4 5) 8

13

Вычислите сумму всех целых решений неравенства .

14

Найдите количество всех целых решений неравенства , принадлежащих промежутку .

15

Найдите число целых решений неравенства .

16

Найдите сумму целых решений неравенства .

17

Укажите число целых решений неравенства .

18

Укажите число целых решений неравенства , принадлежащих отрезку .

19

Укажите середину промежутка множества решений неравенства .

20

Сумма целых отрицательных решений неравенства равна…

8. Уравнения и неравенства, содержащие переменную под знаком модуля.

зада

ния

Условие задания

Варианты ответов

1

Решение неравенства имеет вид

1) 2) 3) 4)

5)

2

Решение неравенства имеет вид

1) 2)

3) 4) 5)

3

Сумма целых решений неравенства равна

1) 12 2) 9 3) 7 4) 6 5) 16

4

Все решения неравенства заполняют на числовой оси промежуток, длина которого равна

1) 2) 3) 1 4) 5)

5

Разность между наибольшим и наименьшим корнями уравнения равна

1) 2) 3)

4) 5) 1

6

Все корни уравнения образуют множество

1) Ø 2) 3) 4) 5)

7

Найти сумму целых решений неравенства .

1) 20 2) 19 3) 13 4) 11 5) 12

8

Решение неравенства имеет вид

1) 2)

3) 4)

5)

9

Больший корень уравнения равен

1) 2 2) 3 3) 5 4) 6 5) 7

10

Сумма значений параметра (или значение, если оно одно), при которых уравнение имеет единственное решение, равна

1) 2 2) 4,4 3) 4 4) 6 5) 2,4

11

Найдите сумму корней уравнения .

12

Найдите сумму целых решений системы неравенств .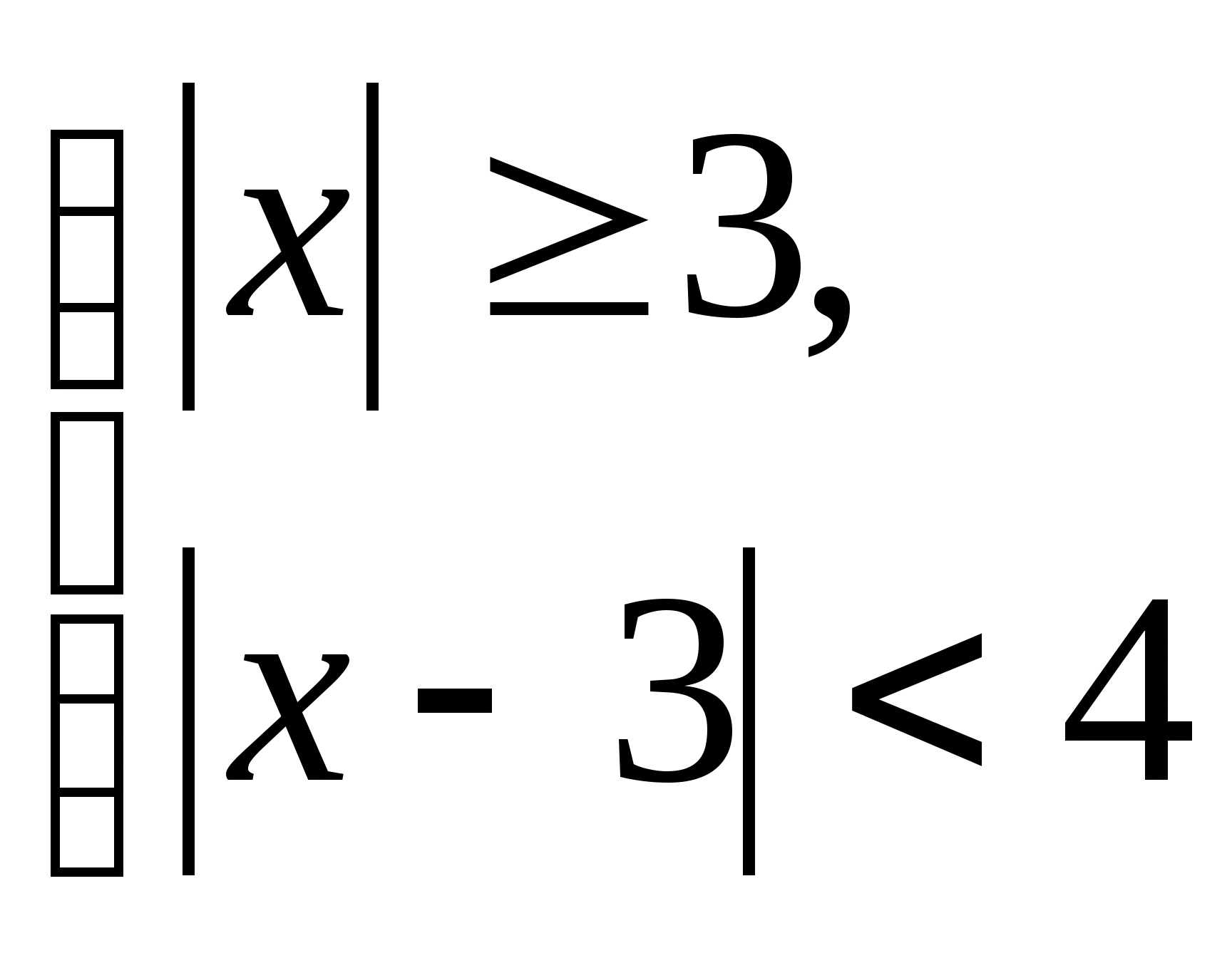

13

Число натуральных корней уравнения равно…

14

Дана функция . Найти наибольшее целое значение , для которого выполняется неравенство .

15

Указать длину промежутка, на котором верно неравенство .

16

Найти среднее арифметическое корней уравнения .

17

Найти наименьшее целое решение уравнения .

18

Если - наименьшее целое решение неравенства , а - количество целых решений данного неравенства, то значение равно…

19

Количество целых значений параметра , при которых уравнение не имеет решений, равно…

20

Найти наименьшее целое значение параметра , при котором уравнение не имеет решений.

9. Иррациональные уравнения и неравенства.

зада

ния

Условие задания

Варианты ответов

1

Пусть - корень уравнения . Тогда значение выражения равно

1) 12 2) 15 3) 14 4) 7 5) 7,5

2

Сумма корней уравнения равна

1) -4 2) 4 3) -3 4) 5 5) -2

3

Произведение корней уравнения равно

1) 25 2) 30 3) 24 4) 28 5) 32

4

Число различных корней уравнения равно

1) 2 2) 1 3) 4 4) 3 5) 5

5

Корни уравнения принадлежат промежутку

1) 2) 3) 4) 5)

6

Количество целочисленных решений неравенства равно

1) 7 2) 15 3) 9

4) другому числу 5) бесконечно

7

Сумма всех корней уравнения равна

1) -18 2) -12 3) -7 4) -6 5) -5

8

Найти число, ближайшее к корню уравнения .

1) 11 2) 5 3) 8 4) 1,5

5) другое число

9

Указать промежуток, содержащий хотя бы один корень уравнения .

1) 2)

3) 4)

5) другой промежуток

10

При каких значениях параметра уравнение имеет два различных корня?

1) 2) 3) 4) 5)

11

Найдите число целых решений неравенства .

12

Найдите сумму целых решений неравенства .

13

Найдите число целых решений неравенства .

14

Найдите число целых решений неравенства .

15

Найдите число целых решений неравенства .

16

Найдите число целых решений неравенства .

17

Среднее арифметическое всех целых решений неравенства равно…

18

Количество всех целых решений неравенства равно…

19

Наибольшее целое решение неравенства равно…

20

Сумма всех целых значений параметра , при которых неравенство верно для любых значений , равна…

10. Тригонометрические преобразования и вычисления.

зада

ния

Условие задания

Варианты ответов

1

Дано: . Вычислить .

1) 2) 3) 4) 5)

2

Дано: . Вычислить .

1) 2) 3) 4) 5)

3

Пусть . Тогда значение выражения равно

1) 2) 3) 4) 5)

4

Пусть . Тогда значение выражения равно

1) ) 3) -0,8 4) 5)

5

После упрощения выражение 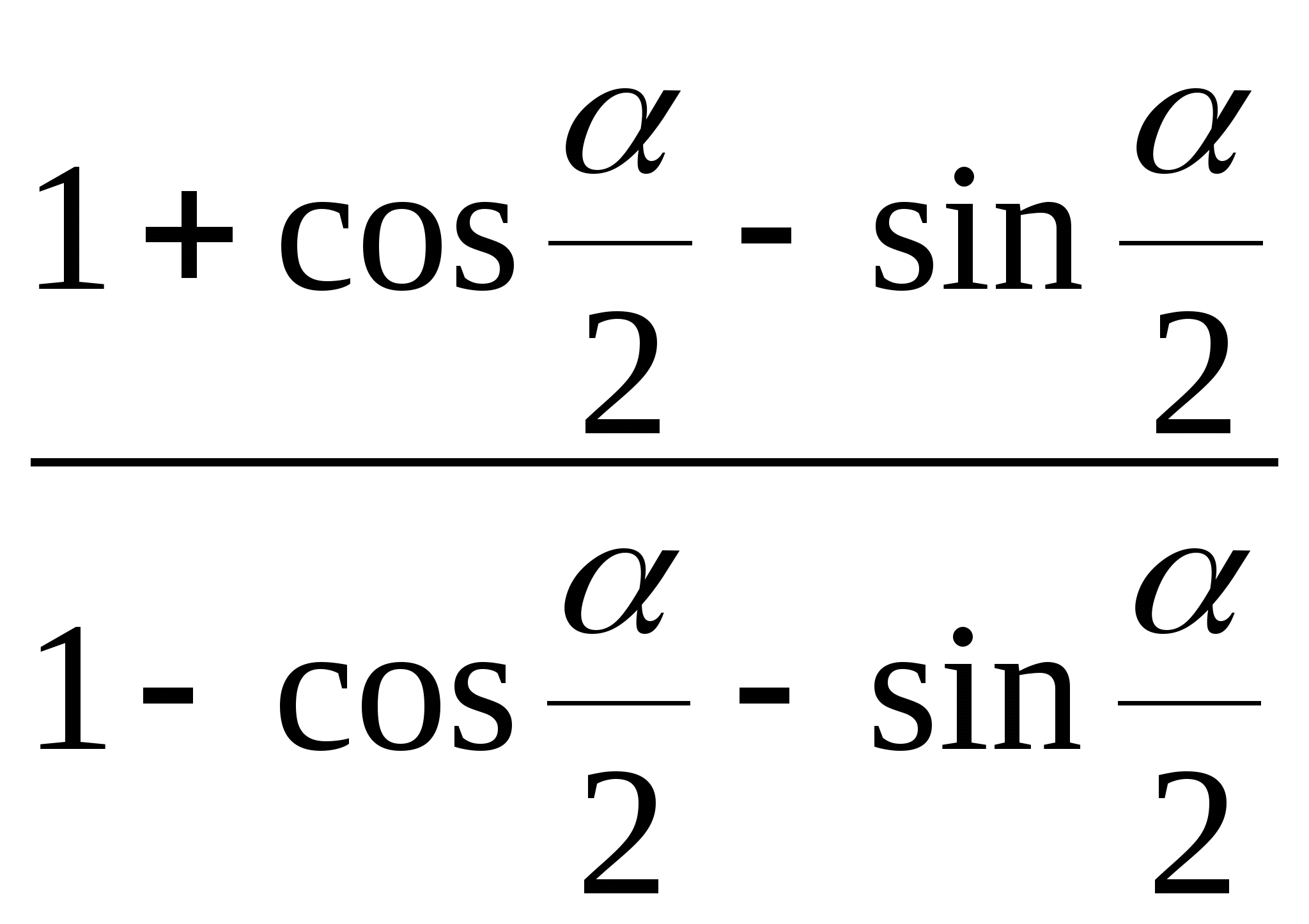имеет вид

1) 2) 3) 4) 5)

6

Значение выражения после упрощения имеет вид

1) 2) 3) 4) 1 5) -1

7

Значение выражения после упрощения равно

1) 2) 3) 4) 5)

8

Выражение после упрощения имеет вид

1) 2) -1

3) 4) 1 5)

9

Выражение после упрощения равно

1) 2) 2 3) 4) -2 5) 1

10

Если и , то значение выражения равно

1) 2) 3) 4) 5)

11

Если , то значение выражения равно

1) 2) 3) 4) 5)

12

Результат упрощения выражения равен

1) 2) 3) 1 4) 5) 2

13

Если , то значение выражения равно

1) 2) 3) 4) 5)

14

Результат упрощения выражения имеет вид

1) 2) 3) 4) 5)

15

Результат вычисления выражения равен

1) 3 2) 2 3) 1 4) -1 5) -2

16

Вычислить .

17

Вычислить .

18

Вычислить .

19

Упростить выражение .

20

Упростить выражение .

11. Действия с обратными тригонометрическими функциями.

зада

ния

Условие задания

Варианты ответов

1

Вычислить .

1) 2) 3) 4) 5)

2

Вычислить .

1) 2) 3)

4) 5)

3

Результат вычисления выражения равен

1) 2) 3) 4) 5)

4

Значение выражения равно

1) 2) 3) 4) 5)

5

Числитель (вместе со знаком) числа , записанного в виде несократимой простой дроби без иррациональности в знаменателе, равен

1) 2) 3) 4) 5)

6

Числитель (вместе со знаком) числа , записанного в виде несократимой простой дроби без иррациональности в знаменателе, равен

1) 2) 3) 4) 5)

7

Результат вычисления выражения равен

1) 2) 3) 4)

5)

8

Результат вычисления выражения равен

1) -0,949 2) 3) 4) 5)

9

Результат вычисления выражения равен

1) 2) 3) 4) 5) 3,873

10

Значение выражения равно

1) 2) 3) 4) 5)

12. Тригонометрические уравнения.

зада

ния

Условие задания

Варианты ответов

1

Найти модуль разности корней уравнения , принадлежащих отрезку .

1) 120 2) 135 3) 90 4) 100 5) 60

2

Найти , где - наименьший, а - наибольший из корней уравнения , принадлежащих отрезку .

1) 180 2) 135 3) 90 4) 75 5) 100

3

Сумма корней уравнения , принадлежащих интервалу , равна

1) -135 2) 180 3) 0 4) 45 5) 135

4

Число различных корней уравнения , удовлетворяющих неравенству , равно

1) 7 2) 5 3) 4 4) 3 5) 2

5

Разность наибольшего и наименьшего корней уравнения , принадлежащих интервалу , равна

1) 225 2) 180 3) -45 4) 45 5) 135

6

Сумма всех различных корней уравнения равна

1) 2) 3) 4) 5)

7

Решение уравнения , принадлежащее интервалу , равно

1) 280 2) 295 3) 300 4) 360 5) 420

8

Найти промежуток, содержащий наименьший по абсолютной величине отрицательный корень уравнения .

1) 2)

3) 4)

5) другой промежуток

9

Число различных решений уравнения на промежутке равно

1) 8 2) 6 3) 4 4) 5 5) 3

10

Найдите промежуток, содержащий сумму наименьшего и наибольшего корней уравнения , лежащих на промежутке .

1) 2)

3) 4)

5) другой промежуток

11

Укажите количество корней уравнения , принадлежащих отрезку .

12

Укажите количество корней уравнения , принадлежащих отрезку .

13

Укажите сумму корней (в градусах) уравнения , принадлежащих отрезку .

14

Укажите сумму корней (в градусах) уравнения , принадлежащих отрезку .

15

Найдите число решений уравнения , принадлежащих отрезку .

16

Количество корней уравнения , принадлежащих отрезку , равно…

17

Количество корней уравнения , принадлежащих отрезку , равно…

18

Количество различных корней уравнения , расположенных на промежутке , равно…

19

Найти количество решений уравнения , если .

20

При каком наименьшем уравнение имеет решение?

13. Тождественные преобразования и вычисления показательных и логарифмических выражений.

зада

ния

Условие задания

Варианты ответов

1

Если , то число равно

1) 2) 3) 4) 5)

2

Если , то число равно

1) 2) 3) 4) 5)

3

Результат вычисления выражения при условии, что , равен

1) -3 2) -2 3) -1,5 4) -2,5 5) -1

4

Результат вычисления выражения при условии, что , равен

1) 0,25 2) 0,5 3) 1,25 4) 0,2 5) 0,75

5

Результат вычисления выражения равен

1) 64 2) 16 3) 128 4) 256 5) 32

6

Если и , то равно

1) 2) 3) 4) 5)

7

Результат вычисления выражения равен

1) 5 2) 9 3) 81 4) 25 5) 10

8

Результат вычисления выражения равен

1) 9 2) 64 3) 18 4) 81 5) 8

9

Значение выражения равно

1) 0 2) 1 3) 2 4) -1 5) 3

10

Результат вычисления выражения равен

1) 2) 3) 2 4) 4 5) 5

11

Результат вычисления выражения равен

1) 4 2) 8 3) 4) 5)

12

Если и , то величина представляется в виде

1) 2) 3) 4) другой дроби, не содержащей логарифмов и букв x,y 5) не выражается через a и b

13

Вычислите .

14

Вычислите .

15

Вычислите .

16

Числа a, b и c положительны. Найти , если .

17

Вычислите .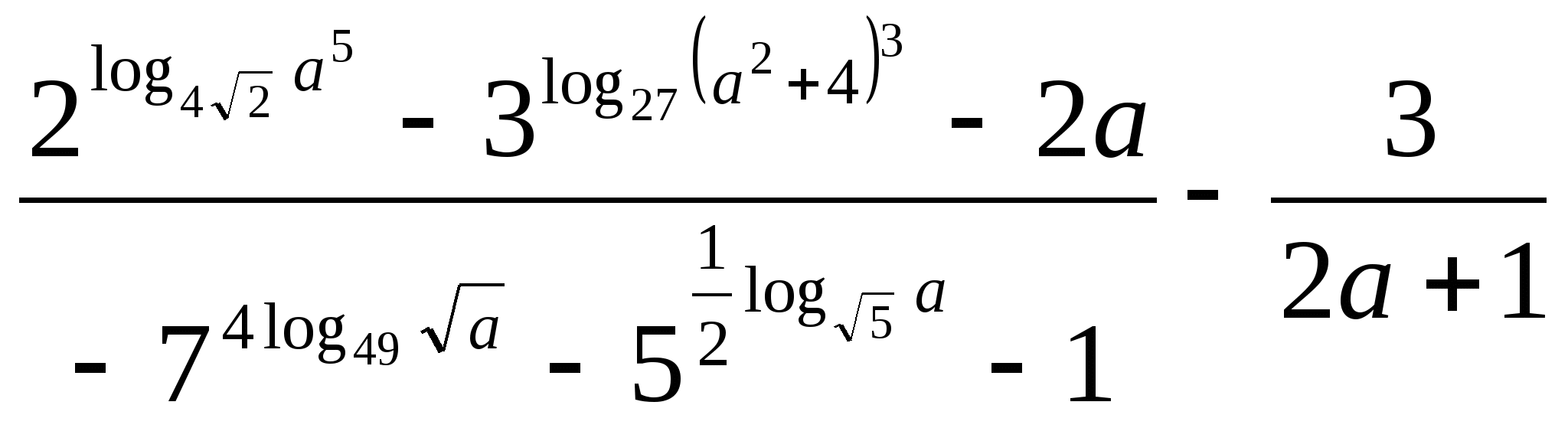

18

Упростить до целого числа .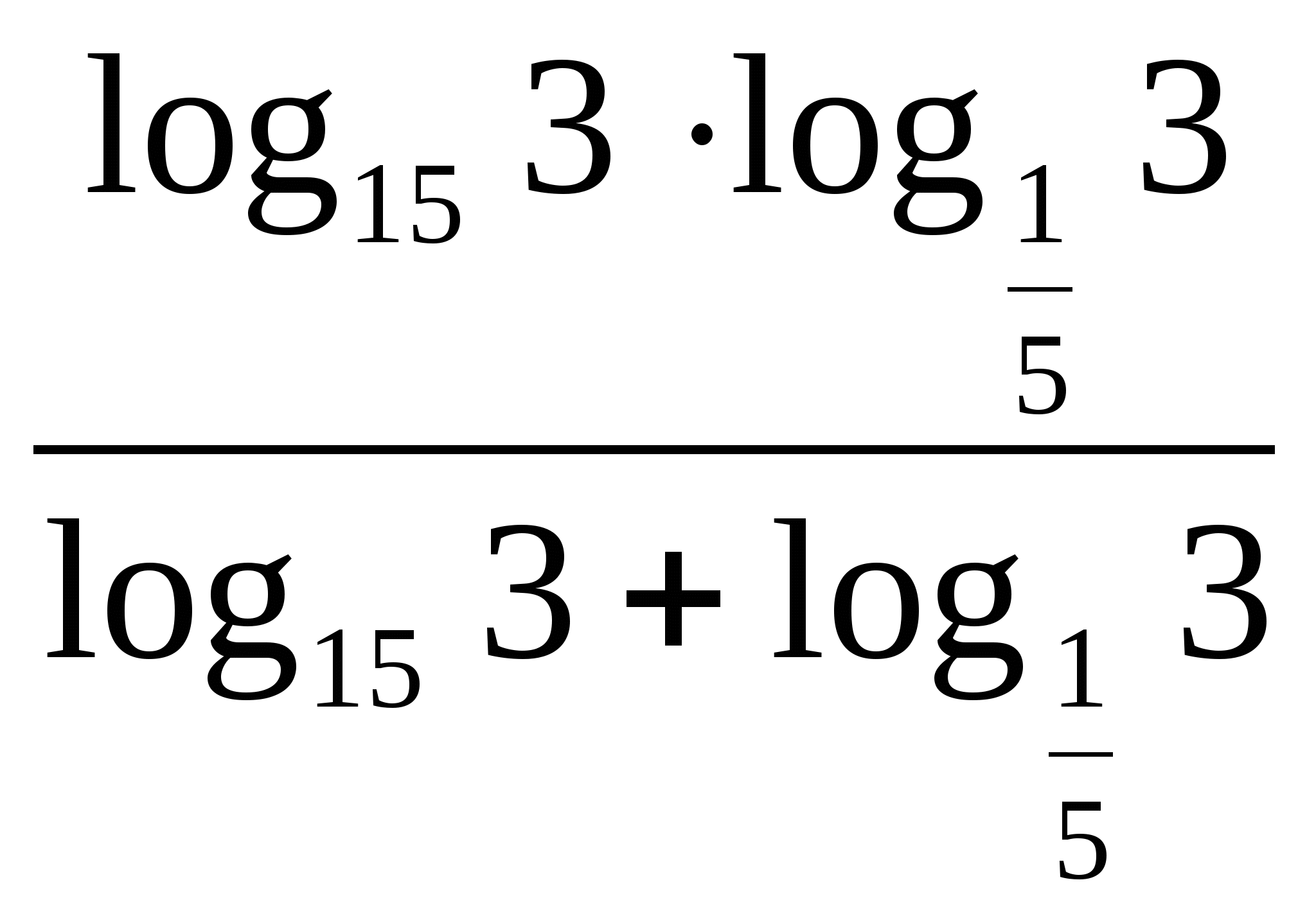

19

Вычислить .

20

Вычислить 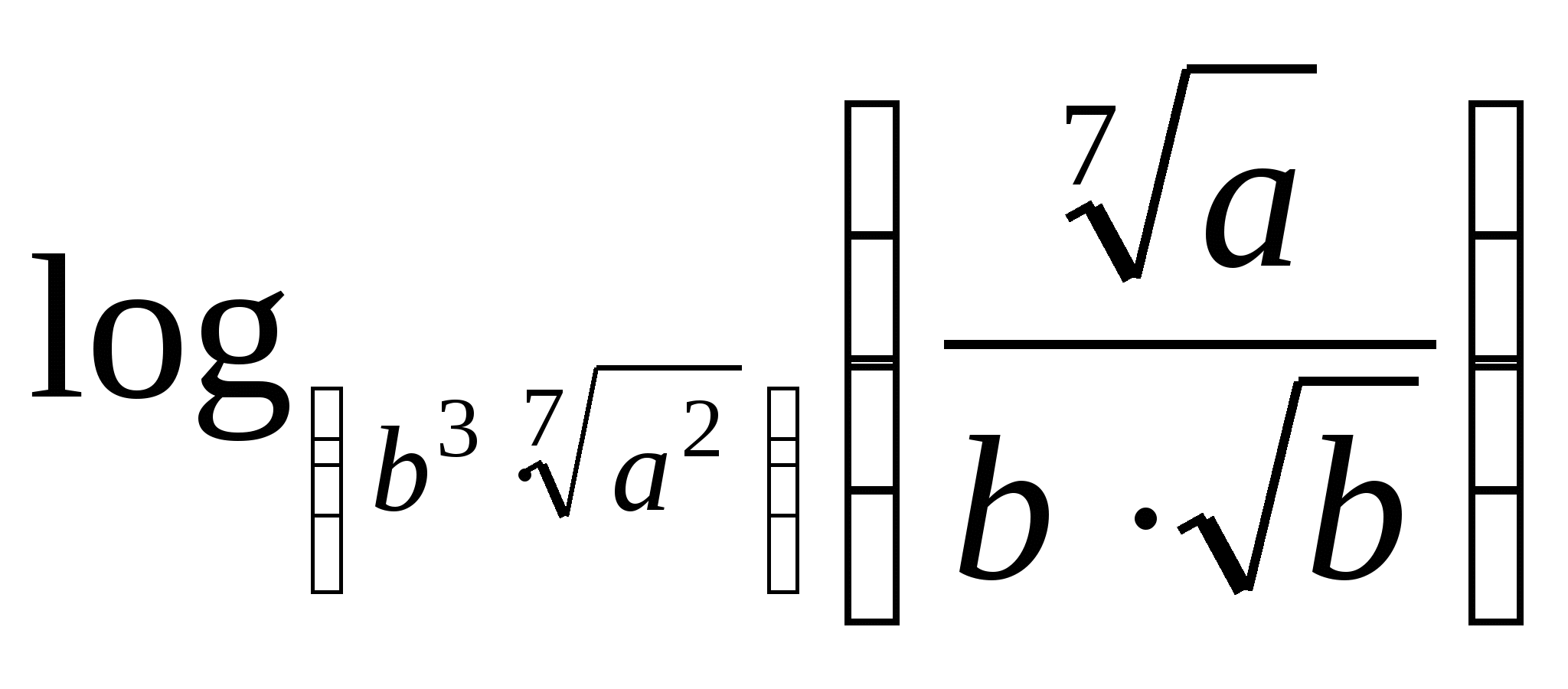, если .

14. Показательные и логарифмические уравнения.

зада

ния

Условие задания

Варианты ответов

1

Корень уравнения принадлежит промежутку

1) 2) 3)

4) 5)

2

Сумма корней уравнения равна

1) 1,0625 2) 9 3) 17 4) 1,125 5) 26

3

Корень уравнения принадлежит промежутку

1) 2) 3) 4) 5)

4

Сумма корней уравнения равна

1) 4,5 2) 2,5 3) 4 4) 3,5 5) 2

5

Если - число корней уравнения , а - его положительный корень, то значение выражения равно

1) 2) 3) 4) 5) 1

6

Сумма корней уравнения равна

1) 2) 3) 2 4) 5)

7

Уравнение имеет ровно один корень, если

1) 2)

3) или 4) 5)

8

Сумма корней уравнения равна

1) 5 2) -2,5 3) -6 4) -5 5) 2,5

9

Произведение корней уравнения равно

1) 27 2) 9 3) 4) 5) 3

10

Сумма корней уравнения равна

1) 2) 3) 4) 5)

11

Сумма корней уравнения равна

1) 10 2) 11 3) 2 4) 15 5) 4

12

Уравнение не имеет корней тогда и только тогда, когда

1) 2) 3) 4) 5)

13

Найти , где - меньший, а - больший корень уравнения .

14

Найти наименьшее целое значение, большее разности большего и меньшего корней уравнения .

15

Найти наименьший корень уравнения .

16

Решить уравнение .

17

Решить уравнение .

18

Решить уравнение .

19

Найти все значения параметра , при которых уравнение имеет единственное решение. Указать наименьшее значение .

20

Найти наибольшее целое значение параметра , при котором уравнение имеет два решения.

15. Показательные и логарифмические неравенства.

зада

ния

Условие задания

Варианты ответов

1

Решить неравенство .

1) 2) 3) 4) 5)

2

Решить неравенство .

1) 2) 3) 4) 5)

3

Решить неравенство .

1) 2) 3) 4) 5)

4

Решить неравенство .

1) 2) 3) 4) 5)

5

Решение неравенства имеет вид

1) 2) 3) 4) 5)

6

Решение неравенства 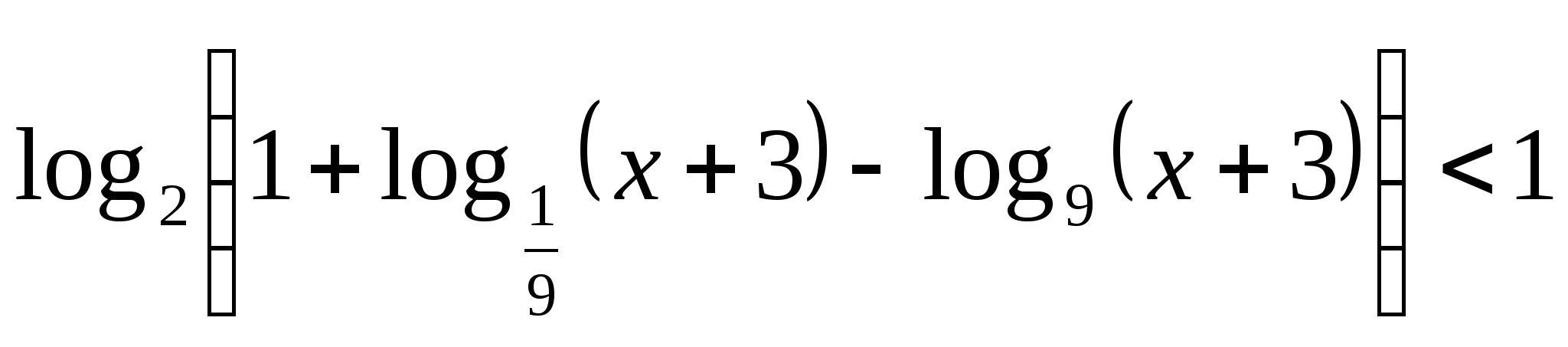имеет вид

1) 2)

3) 4) 5)

7

Решение неравенства имеет вид

1) 2) 3) 4)

5)

8

Количество целых решений неравенства равно

1) 0 2) 1 3) 2 4) 3 5) 4

9

Наименьшее целое , удовлетворяющее неравенству , равно

1) -1 2) -2 3) -3 4) -4 5) -5

10

Все решения неравенства составляют промежуток

1) 2) 3) 4) 5)

11

Наименьшее целочисленное решение неравенства на отрезке равно

1) 4 2) -7 3) 3

4) другому числу

5) не существует

12

Множество решений неравенства на числовой прямой есть

1) вся прямая 2) пустое множество 3) объединение двух интервалов

4) один интервал

5) объединение двух лучей

13

Найдите число целых решений неравенства .

14

Найдите наименьшее целое решение неравенства .

15

Найдите число целых решений неравенства .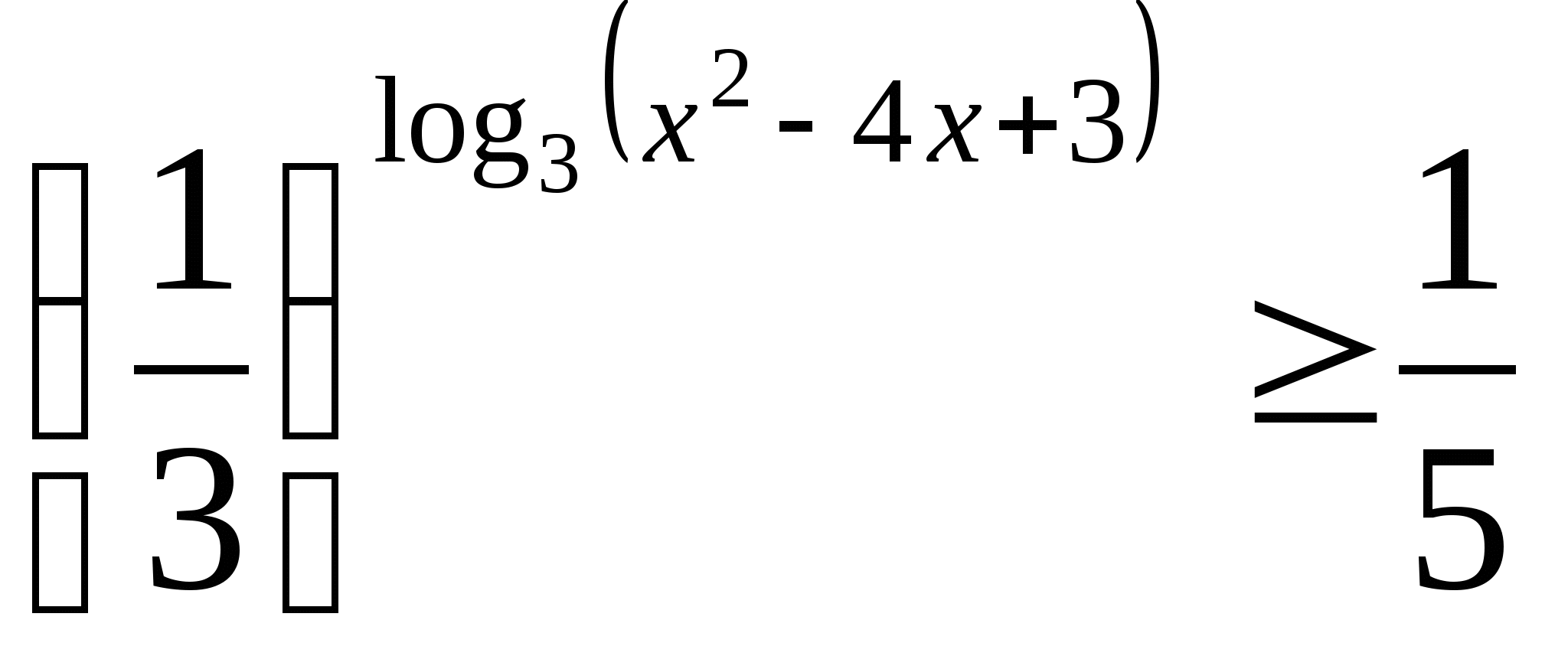

16

Найдите число целых решений неравенства .

17

Найдите число целых решений неравенства .

18

Найдите число целых решений неравенства .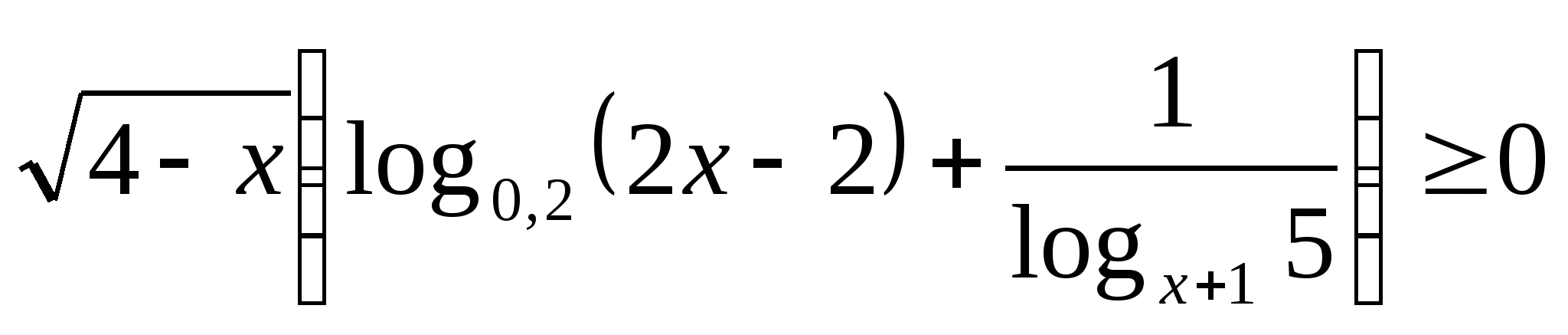

19

Найдите число целых решений неравенства .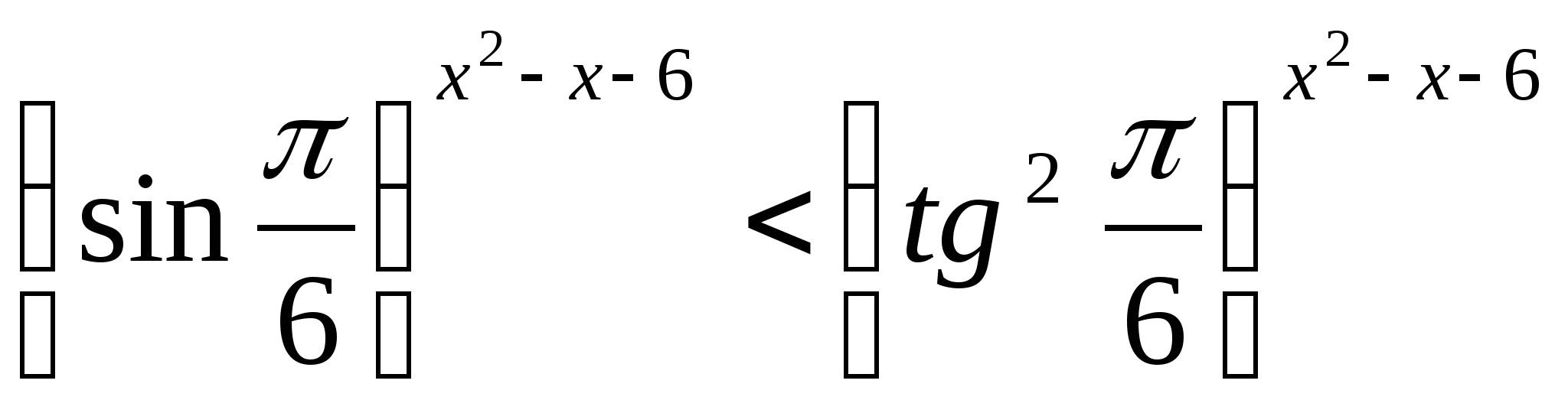

20

Найдите наименьшее целое решение неравенства .

16. Уравнение касательной к графику функции.

зада

ния

Условие задания

Варианты ответов

1

К графику функции в точке с абсциссой проведена касательная. Найти ординату точки графика касательной, абсцисса которой равна .

1) 36 2) 33 3) 35 4) 32 5) 34

2

К графику функции в точке с абсциссой проведена касательная. Найти угол между частью касательной, лежащей в верхней полуплоскости и положительным направлением оси .

1) 2) 3) 4) 5)

3

Найти уравнение касательной к графику функции , которая параллельна прямой, заданной уравнением .

1) 2)

3) 4) 5)

4

На графике функции взята точка . Касательная к графику, проведенная через точку , наклонена к оси под углом, тангенс которого равен . Найти абсциссу точки .

1) 2) 3) 4) 5)

5

В точке пересечения графика функции с осью абсцисс касательная к графику составляет с этой осью угол

1) 2) 3) 4) 5) 0

6

Уравнение касательной к графику функции в точке, где касательная параллельна прямой , имеет вид

1) 2)

3) 4) 5)

7

Пусть - координаты ближайшей к началу координат точки графика функции , где касательная имеет угловой коэффициент . Тогда равно

1) 2) 3) 4) 5)

8

Уравнение касательной к графику функции в не совпадающей с началом координат точке, где эта касательная параллельна оси , имеет вид

1) 2) 3) 4) 5)

9

Пусть касательная к графику функции , проведенная в точке с абсциссой , параллельна касательной к графику функции , проведенной в точке с абсциссой . Тогда, если , то равно

1) 0 2) -3 3) 1 4) 5) -2

10

Если касательная к графику функции , проведенная в точке с абсциссой , параллельна прямой , то равно

1) -12 2) 1 3) 13 4) 16 5) 5

11

Если касательная к графику функции перпендикулярна прямой , то точка касания имеет координаты

1) 2)

3) 4) 5)

12

Касательная к графику функции с угловым коэффициентом пересекает ось абсцисс в точке , равной

1) 2) 3)

4) 5)

13

Через точку (1;4) проходят две касательные к графику функции . Сумма абсцисс точек касания равна

1) 2) 3) 4) 1 5) -1

14

Касательная к графику функции в точке с абсциссой отсекает от положительной полуоси абсцисс вчетверо больший отрезок, чем от отрицательной полуоси ординат, тогда и только тогда, когда значение равно

1) 2) 3) 4) 5)

15

Найдите сумму координат точки с положительной абсциссой, касательная в которой к графику функции проходит через начало координат.

16

Касательная к параболе проходит через начало координат. Найдите значение параметра , при котором абсцисса точки касания положительна, а ордината равна 6.

17

К графику функции в точке проведена касательная. При каком значении параметра касательная проходит через точку М(1;2)?

18

Найти сумму всех действительных значений параметра , при которых график функции касается оси абсцисс.

19

Найти уравнение общей касательной к кривым и . В ответе записать площадь треугольника, отсекаемого касательной от осей координат.

20

К графику функции в точке пересечения его с прямой проведена касательная. Найти площадь треугольника, образованного касательной, заданной прямой и осью абсцисс.

17. Исследование функции с помощью производной.

зада

ния

Условие задания

Варианты ответов

1

Найти все интервалы возрастания функции .

1) 2)

3) 4) 5)

2

Найти сумму значений функции в точках максимумов и минимумов функции.

1) -11 2) -9 3) -7 4) -5 5) -3

3

Значение , где - меньшая из точек минимума функции , равно

1) 0 2) 2 3) 1 4) 3 5)

4

Дана функция , а - точка ее максимума. Тогда значение равно

1) 2 2) 3 3) 1 4) 5)

5

Количество целых значений на интервале возрастания функции равно

1) 0 2) 1 3) 2 4) 3 5) 4

6

Пусть и - соответственно наименьшее и наибольшее значения функции на отрезке . Тогда значение равно

1) 7 2) 8 3) 9 4) 10 5) 11

7

Значение производной функции в точке равно

1) 2) 3) 4) 5)

8

Количество целых значений , принадлежащих интервалу возрастания функции и находящихся в промежутке , равно

1) 3 2) 6 3) 2 4) 4 5) 7

9

Если и - значения функции в точках минимума и максимума соответственно, то значение выражения равно

1) 12 2) 4 3) 9 4) 15 5) -2

10

Найдите все значения параметра , при которых функция возрастает на

1) 2) 3) 4) 5)

11

Найдите число точек экстремума функции .

12

Пусть производная функции имеет вид . Вычислите суммарную длину промежутков возрастания функции .

13

Найдите количество целых чисел, принадлежащих промежутку убывания функции .

14

Вычислите сумму целых значений , принадлежащих промежутку (или промежуткам) возрастания функции .

15

Найти наименьшее значение функции на отрезке .

16

При каком значении максимум функции равен 2?

17

При каких значениях параметра функция имеет наименьшее значение, и это значение меньше 2,5? В ответ запишите наибольшее целое значение.

18

График функции пересекает ось в точке с абсциссой и касается оси в точке с абсциссой . Найти абсциссу точки минимума этой функции.

19

Какая наибольшая площадь может быть у прямоугольника, две вершины которого лежат на оси , а две другие - на графике функции ? В ответ запишите квадрат этой площади.

20

Стороны треугольника лежат на осях координат и на касательной к графику функции в точке, абсцисса которой удовлетворяет условию . Найти утроенное значение , при котором площадь треугольника будет наибольшей.

18. Векторы, их геометрические приложения. Метод координат.

зада

ния

Условие задания

Варианты ответов

1

Длина вектора , если А(-1,5,0) и В(1,1,2), равна

1) 2) 3) 4) 5)

2

Косинус угла между векторами и равен

1) 2) 3) 4) 5)

3

Значения , при которых модуль вектора не превышает 9, удовлетворяет условию

1) 2) 3)

4) 5)

4

В равнобедренном треугольнике с вершинами в точках А(2,3,1), В(1,3,3) и С(2,4,3) длина основания равна

1) 2 2) 3) 3 4) 5)

5

В треугольнике с вершинами в точках А(4,5,1), В(2,3,0) и С(2,1,-1) длина медианы BD равна

1) 1 2) 3) 4) 2 5)

6

Даны векторы , и . Тогда длина вектора равна

1) 2) 3) 4) 5)

7

Даны векторы , и . Тогда скалярное произведение векторов и равно

1) 15 2) 17 3) 20 4) 25 5) 12

8

Даны векторы , и . Тогда угол между векторами и равен

1) 2)

3) 4)

5)

9

В треугольнике с вершинами А(1,0,3), В(1,1,-3) и С(3,1,-1) длина меньшей стороны равна

1) 8 2) 3) 2 4) 5)

10

В треугольнике с вершинами А(3,7,-4), В(2,-1,1) и С(1,3,0) длина средней линии, параллельной АС, равна

1) 2) 9 3) 6 4) 5) 3

11

Если в параллелограмме ABCD заданы , то сумма координат точки С равна

1) 1 2) -1 3) 2 4) -2 5) 3

12

В треугольнике ABC точка M - середина стороны AB, точка N - середина стороны BC, . Тогда сумма координат вектора равна

1) 1 2) 2 3) 3 4) -1 5) -2

13

Если в параллелограмме ABCD заданы , то сумма координат точки пересечения диагоналей параллелограмма равна

1) 7 2) 6 3) 5 4) 4 5) 3

14

Если в четырехугольнике ABCD заданы , а векторы и - его диагонали, то модуль скалярного произведения векторов и равен

1) 2 2) 3 3) 4 4) 5 5) 6

15

Найдите , если и .

16

Дан вектор 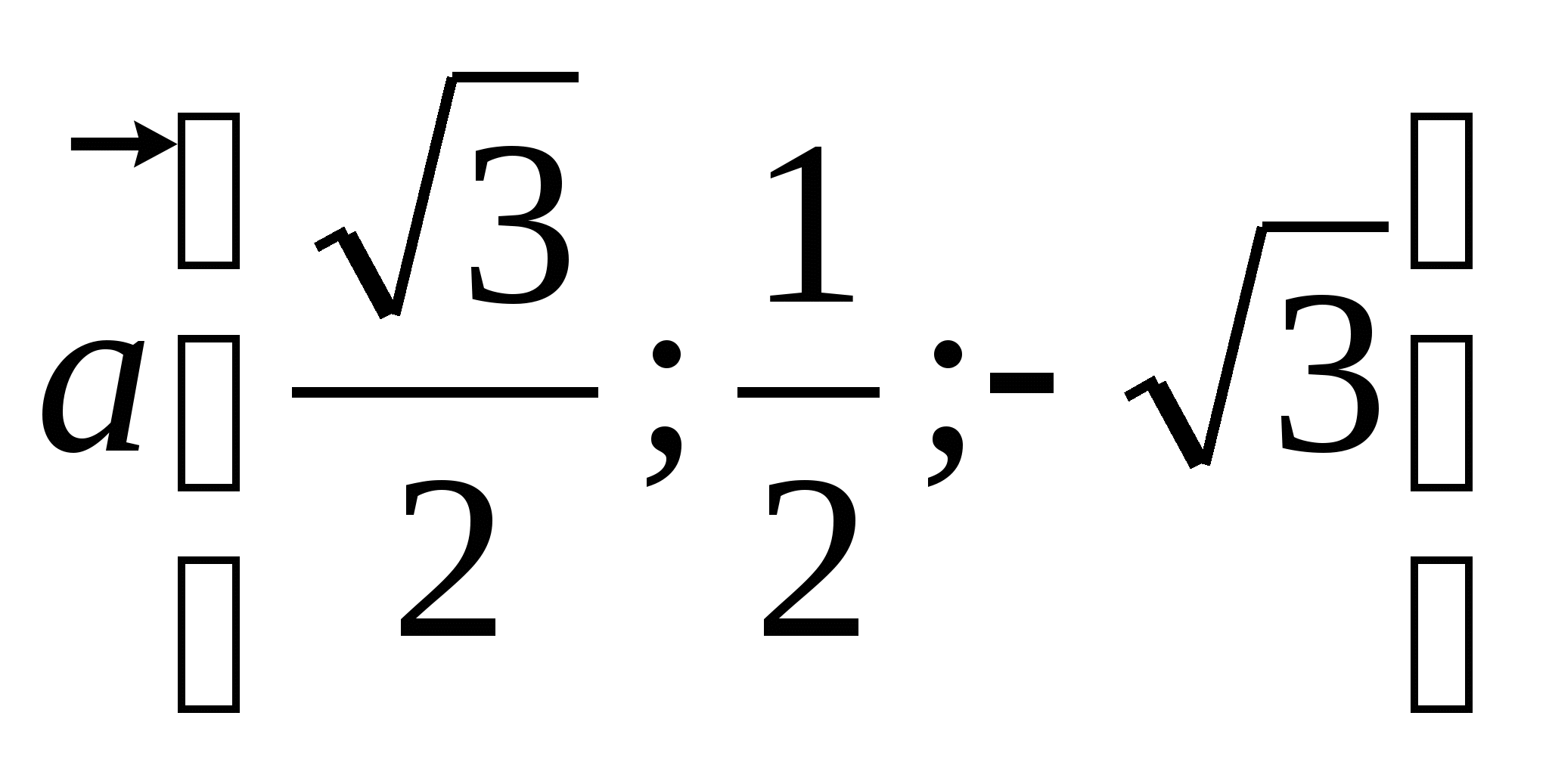. Найдите угол (в градусах) между данным вектором и осью .

17

Найдите , если делит угол между векторами и пополам.

18

Вектор имеет длину, равную 1 см. Векторы и образуют угол в . Вектор имеет длину, равную см. Найти длину вектора .

19

Дано: . Найти скалярное произведение векторов и .

20

Вершины выпуклого четырехугольника находятся в точках A(2;7), B(14;-1), C(7;-10), D(-3;-8). Точки M и N являются серединами сторон AB и CD соответственно. Укажите сумму координат середины отрезка MN.

19. Задачи по планиметрии.

зада

ния

Условие задания

Варианты ответов

1

Пусть основания трапеции равны 8 см и 2 см, а высота равна 5 см. Тогда расстояние от точки пересечения диагоналей до меньшего основания равно

1) 2 см 2) 1,5 см 3) 2,5 см 4) 4 см 5) 1 см

2

В ромб вписана окружность радиуса 3 см, а его тупой угол равен 150. Тогда площадь ромба равна

1) 28 см² 2) 72 см² 3) 18 см² 4) 36 см² 5) 48 см²

3

Если в равнобедренном треугольнике длина основания относится к длине боковой стороны как 4:3, а его периметр равен 20 см, то длина основания треугольника равна

1) 10 см 2) 8 см 3) 6 см

4) 12 см 5) 9 см

4

Если внутренние углы выпуклого четырехугольника относятся как 2:2,5:9,5:10, то меньший угол четырехугольника равен

1) 30 2) 45 3) 60 4) 15 5) 20

5

Если в окружности радиуса 26 см проведена хорда длиной 48 см, то длина отрезка, соединяющего середину этой хорды с центром окружности, равна

1) 4 см 2) 5 см 3) 10 см 4) 12 см 5) 8 см

6

Если из точки, взятой на окружности, проведены диаметр и хорда, равная радиусу, то угол между диаметром и хордой равен

1) 90 2) 30 3) 45 4) 60 5) 120

7

Если биссектриса внешнего угла равнобедренного треугольника ABC при основании AC образует с основанием угол в 132, то угол ABC равен

1) 15 2) 30 3) 18 4) 45 5) 12

8

Если из точки А, взятой на окружности, проведены две взаимно перпендикулярные хорды AB и AC, и хорда AC стягивает дугу в 54, то угол ACB равен

1) 36 2) 72 3) 63 4) 54 5) 126°

9

Если треугольник, периметр которого равен 15 см, делится медианой на два треугольника с периметрами 11 см и 14 см, то длина медианы равна

1) 6 см 2) 3 см 3) 7 см 4) 4 см 5) 5 см

10

Если одна из сторон треугольника на 3 см меньше другой, высота делит третью сторону на отрезки длиной 5 см и 10см, то периметр треугольника равен

1) 25 см 2) 40 см 3) 32 см 4) 20 см 5) 42 см

11

Если в равнобедренном треугольнике длина основания равна 12 см. а его периметр равен 32 см, то радиус окружности, вписанной в треугольник, равен

1) 4 см 2) 6 см 3) 3 см 4) 5 см 5) 2 см

12

Если высоты равнобокой трапеции делят ее на квадрат и два равнобедренных треугольника, а ее боковая сторона равна см, то сумма ее оснований равна

1) 12 см 2) 20 см 3) 22 см 4) 16 см 5) 18 см

13

Если в равнобокую трапецию вписана окружность радиуса 6 см, точка касания делит боковую сторону на отрезки, разность между которыми равна 5 см, то средняя линия трапеции равна

1) 10 см 2) 11 см 3) 12 см 4) 13 см 5) 15 см

14

Если из точки окружности проведены диаметр и хорда, длина которой равна 30 см, проекция хорды на диаметр относится к радиусу окружности как 18:25, то радиус окружности равен

1) 5 см 2) 10 см 3) 15 см 4) 20 см 5) 25 см

15

В прямоугольном треугольнике ABC с катетом AB=9 и медианой BM=7, проведенной к гипотенузе AC, расстояние между точкой M и основанием H высоты BH равно

1) 2) 3) 4) 5) другому числу

16

Отрезок длины 7, соединяющей боковые стороны трапеции и параллельный ее основаниям, равным 9 и 3, делит площадь трапеции в отношении

1) 5:4 2) 5:8 3) 2:1 4) 5) в другом отношении

17

Диагонали AC и BD четырехугольника ABCD пересекаются в точке О. Площади треугольников AOB и COD равны соответственно 3 м² и 4 м², а площадь треугольника BOC втрое больше площади треугольника COD. Найдите площадь четырехугольника ABCD.

18

Биссектриса острого угла прямоугольного треугольника делит противолежащий катет на отрезки 3 и 5. Следовательно, второй катет равен…

19

Окружность, проходящая через вершины B и C треугольника ABC, пересекает стороны AB и AC в точках M и N соответственно, а отрезки BN и CM пересекаются в точке K. Если и , то величина угла BKC (в градусах) равна…

20

Средняя линия равнобочной трапеции, описанной около круга, равна 170. Определить радиус круга, если нижнее основание трапеции больше верхнего на 160.

20. Задачи по стереометрии.

зада

ния

Условие задания

Варианты ответов

1

Известно, что высота правильной четырехугольной призмы равна , а площадь диагонального сечения равна 4 см². Тогда площадь основания равна

1) 16 см² 2) 4 см² 3) 8 см² 4) 2 см² 5) см²

2

Пусть в треугольной пирамиде все боковые грани образуют с плоскостью основания углы по 60, и в основание вписан круг площадью 9 см². Тогда высота пирамиды равна

1) 3 см 2) см 3) 3 см

4) см 5) 9 см

3

Если образующая конуса равна 6 см, а угол при вершине осевого сечения равен 60, то площадь поверхности шара, вписанного в этот конус, равна

1) см² 2) см² 3) см² 4) см² 5) см²

4

Высота правильного параллелепипеда равна 3 см. Через одну из сторон нижнего основания и противоположную - верхнего проведена плоскость. Объем параллелепипеда равен 48 см³. Тогда площадь сечения равна

1) 15 см² 2) 20 см² 3) 25 см² 4) 12 см² 5) 18 см²

5

В основании пирамиды лежит прямоугольный треугольник с катетами 6 см и 8 см. Объем пирамиды равен 40 см³. Все боковые ребра наклонены к плоскости основания под одинаковым углом. Этот угол равен

1) 45 2) 30 3) 60 4) 15 5) 2230

6

Конус вписан в шар радиуса 3 см, угол при вершине осевого сечения конуса равен 60. Площадь боковой поверхности конуса равна

1) см² 2) см² 3) см² 4) см² 5) см²

7

Если сфера проходит через все вершины куба с длиной ребра 9, то радиус сферы равен

1) 2) 3) 4)

5)

8

Если сфера радиуса 1 касается всех граней правильной треугольной призмы, то длина ребра основания призмы равна

1) 2) 3) 4) 5)

9

Сфера вписана в конус, образующая которого равна 12, а радиус основания - 3. Найдите длину линии касания сферы и боковой поверхности конуса.

1) 2) 3) 4) 5)

10

Если сфера радиуса 5 см проходит через все вершины прямоугольного параллелепипеда, в основании которого прямоугольник со сторонами 3 см и 4 см, то объем этого параллелепипеда (в куб. см) равен

1) 2) 3) 4) 5)

11

Если диагональ куба равна 12 см, то площадь (в кв. см) сферы, касающейся всех граней этого куба, равна

1) 2) 3) 4) 5)

12

Если в треугольной пирамиде SABC с высотой SH=3 все боковые ребра наклонены под углом 30 к плоскости основания ABC, а угол BAC равен 45, то длина ребра BC равна

1) 2) 3) 4) 5) другому числу

13

Если в правильной треугольной пирамиде SABC объемом 21 точка O - центр вписанной в треугольник SBC окружности, а боковое ребро в 7 раз больше ребра основания ABC, то объем пирамиды OABC равен

1) 7 2) 3 3) 4) 5) другому числу

14

В прямоугольном параллелепипеде ABCDABCD с ребрами AA=6, AB=5 и AD=8 косинус угла BAD равен

1) 2) 3) 4) 5) другому числу

15

Объем правильной треугольной призмы равен 36, а высота призмы вдвое больше стороны основания. Чему равна сторона основания этой призмы?

1) 2) 3) 4 4) 5) 6

16

Боковые ребра правильной треугольной пирамиды взаимно перпендикулярны, а сторона основания равна . Найдите объем этой пирамиды.

17

Сторона основания правильной треугольной пирамиды равна 6, а двугранный угол при основании равен 45. Найти объем пирамиды.

18

В основании пирамиды лежит прямоугольный треугольник, гипотенуза которого 12 см, а один из острых углов вдвое меньше другого. Вершина пирамиды удалена от всех вершин треугольника на 10 см. Найти , где - объем пирамиды.

19

Стороны основания треугольной пирамиды равны 39 см, 39 см и 30 см. Боковые грани пирамиды наклонены к плоскости основания под углом 60. Найти , где - объем пирамиды.

20

В шар вписан конус. Площадь осевого сечения конуса равна , а угол между высотой и образующей равен 45. Найдите объем шара.

Ответы.Тест 1

1

2

3

4

5

6

7

8

9

10

2

3

4

2

1

2

2

3

3

2

11

12

13

14

15

16

17

18

19

20

4

4

4

2

3

3

2

5

5

1

Тест 2

1

2

3

4

5

6

7

8

9

10

3

4

3

5

2

5

3

3

5

1

11

12

13

14

15

16

17

18

19

20

1

2

4

3

3

1

3

1

4

1

Тест 3

1

2

3

4

5

6

7

8

9

10

4

2

1

2

4

1

5

4

3

4

11

12

13

14

15

16

17

18

19

20

-13

3

-2

1

-2

1

-1

-0,2

-49

5

Тест 4

1

2

3

4

5

6

7

8

9

10

3

3

3

4

2

2

3

1

2

5

11

12

13

14

15

16

17

18

19

20

1

5

5

24

10

-0,75

8,5

1

11

10

4Тест 5

1

2

3

4

5

6

7

8

9

10

2

1

3

2

2

3

2

1

3

4

11

12

13

14

15

16

17

18

19

20

4

1

4

3

38

31

10

11

7

8

Тест 6

1

2

3

4

5

6

7

8

9

10

3

3

5

3

2

3

2

1

2

1

11

12

13

14

15

16

17

18

19

20

4

1

3

2

5

-2

-15

-0,9

-17

2

Тест 7

1

2

3

4

5

6

7

8

9

10

3

5

1

5

1

3

4

4

2

4

11

12

13

14

15

16

17

18

19

20

2

2

12

1

4

21

2

3

1

-7

Тест 8

1

2

3

4

5

6

7

8

9

10

2

3

2

1

3

5

5

4

4

2

11

12

13

14

15

16

17

18

19

20

8

18

9

2

2

-1

-1

-3

3

-8

Тест 9

1

2

3

4

5

6

7

8

9

10

3

3

2

1

5

3

3

5

5

5

11

12

13

14

15

16

17

18

19

20

6

9

1

1

1

5

1

2

3

10

Тест 10

1

2

3

4

5

6

7

8

9

10

1

4

1

1

3

1

2

4

2

4

11

12

13

14

15

16

17

18

19

20

3

4

1

3

4

1

-1

1

4

0

Тест 11

1

2

3

4

5

6

7

8

9

10

1

2

1

1

2

3

2

4

3

5

11

12

13

14

15

16

17

18

19

20

2,6

0,96

40

-1

3

0

-1

540

140

45

Тест 12

1

2

3

4

5

6

7

8

9

10

3

5

2

1

5

1

3

4

1

4

11

12

13

14

15

16

17

18

19

20

1

4

900

-210

3

2

4

1

2

-5

Тест 13

1

2

3

4

5

6

7

8

9

10

5

3

2

1

4

4

2

5

1

4

11

12

13

14

15

16

17

18

19

20

2

2

1

10

1

2

1

1

-3,5

-0,1

Тест 14

1

2

3

4

5

6

7

8

9

10

4

3

1

4

5

2

3

1

1

4

11

12

13

14

15

16

17

18

19

20

4

2

30

2

1,2

3

256

8

-6

-3

Тест 15

1

2

3

4

5

6

7

8

9

10

2

3

1

2

3

4

5

3

4

5

11

12

13

14

15

16

17

18

19

20

1

3

5

2

2

1

3

3

4

2

Тест 16

1

2

3

4

5

6

7

8

9

10

3

4

5

3

4

3

5

2

5

2

11

12

13

14

15

16

17

18

19

20

5

4

2

2

4

-1

0,375

0

25

60

Тест 17

1

2

3

4

5

6

7

8

9

10

4

3

3

5

4

3

2

2

2

1

11

12

13

14

15

16

17

18

19

20

3

7

7

-5

0

-0,5

17

4

432

-2

Тест 18

1

2

3

4

5

6

7

8

9

10

5

5

5

4

1

2

2

2

2

5

11

12

13

14

15

16

17

18

19

20

2

4

1

2

20

150

12

0,5

29

2

Тест 19

1

2

3

4

5

6

7

8

9

10

5

2

2

1

3

4

5

3

5

2

11

12

13

14

15

16

17

18

19

20

3

4

4

5

2

1

20

6

105

75

Тест 20

1

2

3

4

5

6

7

8

9

10

2

3

1

2

1

1

2

2

5

1

11

12

13

14

15

16

17

18

19

20

5

4

4

3

4

288

9

144

1800

4