- Учителю
- Урок по математике на тему 'производная и ее применение' (11 класс)
Урок по математике на тему 'производная и ее применение' (11 класс)
Итоговый урок по теме: «Производная и ее применение».
Цели урока:
-
обучающие цели:
-
систематизация и обобщение знаний учащихся по теме;
-
проверка усвоения учащимися пройденного материала;
-
-
развивающие цели:
-
развитие познавательного интереса;
-
развитие мыслительной деятельности;
-
развитие навыков обработки информации;
-
-
воспитательные цели:
-
воспитание ответственности;
-
воспитание духовности и культуры.
-
Оборудование:
-
мультимедийная установка,
-
сигнальные карточки,
-
копировальная бумага,
-
раздаточный материал: карточки для теста, фрагменты текста.
Ход урока:
I. Организационный момент.
II. Математический диктант (учащиеся пишут "под копирку" с последующей проверкой):
№ Зад.
I вариант
II вариант
1)
Записать определение производной с помощью математических символов.
Записать правила дифференцирования.
2)
Чему равна производная степенной функции.
Чему равна производная логарифмической функции.
3)
Условие возрастания функции на промежутке.
Необходимое условие экстремума
4)
Достаточное условие экстремума.
Условие убывания функции на промежутке.
5)
Геометрический смысл производной.
Уравнение касательной.
III. Задачи картинки: (учащимся выдаются карточки с цифрами 1, 2, 3, через проектор показываются картинки, после обдумывания по команде учителя учащиеся поднимают сигнальные карточки с номером верного ответа и фиксируют ответ в бланке ответов.)
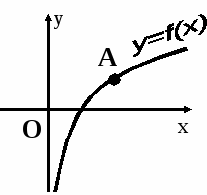
-
Какое значение принимает производная функции в точке А? Ответы:
$ 1) f'(x)=0;
$ 2) f'(x) <0;
$ 3) f'(x)> 0.
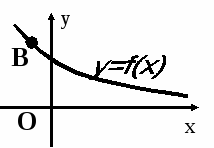
2.Какое значение принимает производная функции y=f(x) в точке В?
Ответы:
1) f'(x) =0;
2) f'(x) < 0;
3) f'(x) >0.
3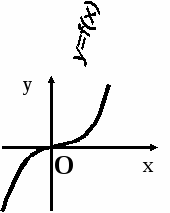 .Назовите промежуток возрастания функции.
.Назовите промежуток возрастания функции.
Ответы:
1) х <0;
2) x>0;
3) - <x <+.
4.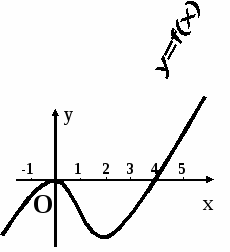 Назовите промежуток убывания функции.
Назовите промежуток убывания функции.
Ответы:1) 0 <x <3;
2) 0 <x <2
3) x >2.
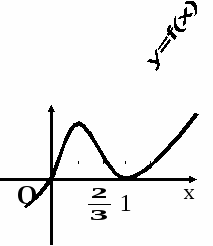
5. Назовите точки, в которых производная равна нулю.
Ответы: 1) ![]() ; 1.
; 1.
2) 0; 1.
3) 0; ![]() ; 1.
; 1.
IV. Тест: нахождение наибольшего и наименьшего значения функции на отрезке.
В какой из точек указанного отрезка функция достигает наибольшего (I, IV вариант), наименьшего (II, III вариант) значения?
I.Вариант: y=x3-3x
[-3;-2]
[-2;-1]
[-2;0]
[-2;2]
[-2;3]
Только на левом конце
Только на правом конце
Только во внутренней точке
Более чем в одной точке
Ни в одной точке
II.Вариант: y=x3-3x2
[-3-1]
[-1; 0]
[-1;1]
[-1;2]
[-1;3]
Только на левом конце
Только на правом конце
Только во внутренней точке
Более чем в одной точке
Ни в одной точке
I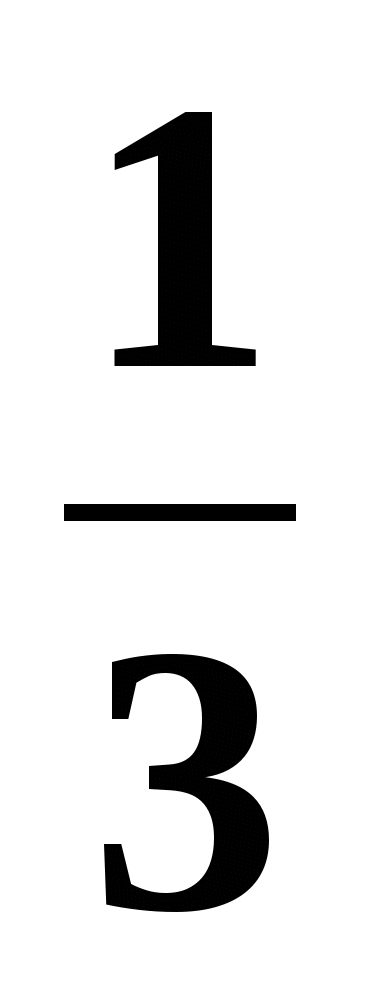 II.Вариант:
II.Вариант:
X2![]() , X≠0
, X≠0
Y=
0, X=0
[-3;-1]
[-1;0]
[0;1]
[1;3]
[3;5]
Только на левом конце
Только на правом конце
Только во внутренней точке
Более чем в одной точке
Ни в одной точке
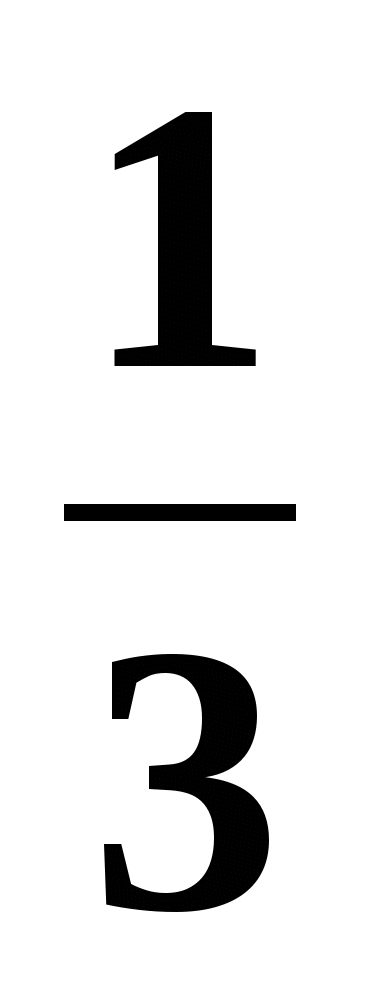 IV.Вариант:
IV.Вариант:
X![]() , X≠1
, X≠1
Y=
0, X=1
[-4;-2]
[-2;0]
[-1;1]
[0;1]
[1;5]
Только на левом конце
Только на правом конце
Только во внутренней точке
Более чем в одной точке
(Учащимся нужно отметить знаком «+» каждое найденное соответствие между вопросом и ответом. I и II варианты - более лёгкие, III и IV варианты - более сложные. Уровень сложности выбирают сами учащиеся. )
V.Верно ли, что:
а) если производная функции в некоторой точке равна нулю, то в этой точке имеется экстремум?
б) наибольшее или наименьшее значение функции на некотором отрезке наблюдается или в стационарных точках, или на концах отрезка?
в) функция f(x) и функция (f(x)) n, где n-натуральное число, на некотором промежутке принимают наибольшее (наименьшее) значение в одной и той же точке?
г) если производная больше нуля на некотором промежутке, то функция возрастает на этом промежутке?
д) в точке перегиба дифференцируемая функция меняет направление выпуклости?
При ответе на данные вопросы учащиеся должны поднять карточку с цифрой «0»,если утверждение неверно, или с цифрой «1», если утверждение верно.
VI.Запиши ответ (учащиеся пишут "под копирку" с последующей проверкой):
1.запиши промежутки монотонности функции и назови её экстремумы:
а )
)
б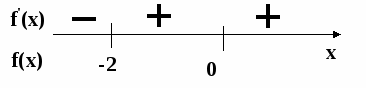 )
)
в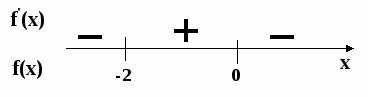 )
)
2) сравните, не прибегая к вычислениям, следующие значения производной функции, график которой изображен на рисунке:
а) f'(-2) и f'(1);
б) f'(2) и f'(3).
VII.Домашнее задание («Математика вокруг нас»):
а) Исследование свойств функции:
Отправимся в путь на автомобиле по шоссе из города А в город В. Будем внимательно приглядываться к рельефу дороги. Ровный участок дороги ассоциируется с термином «константа». Дорога идет под уклон-это монотонное убывание. Кончился спуск, и води-тель включает газ, отмечая тем самым точку минимума. Дорожный знак указывает подъем, а у математика наготове свой термин - монотонное возрастание. Перевалим через гребень холма - пройдена точка максимума. И снова началось монотонное убывание-спуск. На холмах дорога выпукла, в ложбинах вогнута, не отмеченные дорожными знаками стыки таких участков дороги математик отметит про себя как точки перегиба.
Математические понятия, о которых шла речь в этом описании, делятся на две группы : одни описывают поведение функции в окрестности некоторых характерных точек, другие - в некоторых промежутках. Чтобы в общих чертах воспроизвести профиль дороги, достаточно описать поведение функции сначала в окрестностях характерных точек, а затем в промежутках между этими точками. Воспроизведите профиль дороги.
б) Сказка про Функцию.
Жила-была тетушка Функция, и было у неё много-много дочек-точек. Жили они все в некоторой области Определения. Дружная была семья, работящая. Дочери росли и выросли, наконец, настоящими красавицами. Пора настала им замуж выходить. В соседней области, которая называлась область Значений, было много парней, так, что каждая точка смогла найти своего суженного.
Решила мать-Функция собрать своих дочерей и узнать кого они выбрали в мужья. Вот собрались они все, уселись рядком и стали о своих женихах рассказывать. Все рассказывают. Только две сестры сидят важно, словом не обмолвятся. Стали их расспрашивать. Наконец промолвила одна: «Что там ваши парни, ничем они не примечательны, да и правду сказать, каковы невесты таковы и женихи. Хорошо, что хоть кто-нибудь на вас позарился. Вот мой суженный в своей окрестности самый большой и имя у него красивое - Максимум».
Обиделись сестры, но промолчали. А тут другая заговорила: «Правду молвишь, сестрица. Скучно вы, остальные точки, будете жить. Разве с вашими будущими мужьями можно чего-нибудь добиться? Вот у меня муж будет тоже особенный - самый маленький в своей окрестности. И не важно, что маленький, главное, самый».
Рассердилась мать и решила проучить дочерей-зазнаек. И говорит она им: «Ну, дочери мои разлюбезные, благославляю я вас. Живите с мужьями своими в любви да согласии. А от меня, на жизнь новую, приданое примите. Есть у меня для каждой из вас штуковина одна, производная называется. Дарю я вам шкатулочки, где лежит столько золота, каков модуль значения производной, соответствующего каждой из вас. Поблагодарили дочери мать, поклонились в пояс и отправились каждая со своим приданным в новую жизнь. Больше всех радовались наши зазнайки. Уж у нас-то, думают, наверняка, самое лучшее приданное, раз у нас женихи самые-самые. А как открыли они свои шкатулки - даже золотой песчинки не нашли.
О какой теореме шла речь в сказке?
Чему равно значение производной в этих точках?
Нарисуйте пример графика функции о которой могла идти речь.
в) Обратимся к классикам… (Задача Льва Толстого):
В рассказе Л.Н.Толстого «Много ли человеку земли надо» идет речь о том как Пахом, который мечтал о собственной земле и, собрав наконец желаемую сумму, предстал перед требованием старшины: «Сколько за день земли обойдешь - вся твоя будет за 1000 рублей, но если к заходу солнца не возвратишься на место, с которого вышел, пропали твои деньги.»
В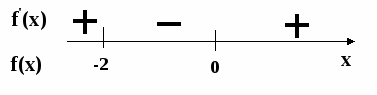 ыбежал утром Пахом, прибежал на место и упал без чувств, обежав четырехугольник перимет-ром 40 км.
ыбежал утром Пахом, прибежал на место и упал без чувств, обежав четырехугольник перимет-ром 40 км.
1) Какую площадь в данном случае имеет участок?
2) Является ли данная площадь наибольшей?
3) Из прямоугольников данного периметра выбрать тот, у которого площадь наибольшая.
г) Творческое задание:
Придумать или подобрать в литературе пример использования свойств производной функции в жизненных ситуациях.
VIII Итог урока:
Повторить: для решения каких задач используется производная;
алгоритмы решения основных задач с использованием производной.
На каждом этапе урока деятельность учащихся оценивается и в конце урока каждому выставляется итоговая оценка.