Урок алгебры 7 класс. Линейное уравнение с двумя переменными и его график.

Урок алгебры 7 класс.

Тема урока. Линейное уравнение с двумя переменными и его график.

1 модуль. Урок-установка к теме: «Системы линейных уравнений с двумя переменными».

Цели урока:

1. Образовательная. Формирование понятий: линейное уравнение с двумя переменными, решение линейного уравнения с двумя переменными, график линейного уравнения с двумя переменными, система линейных уравнений с двумя переменными; формирование умений строить графики линейных уравнений с двумя переменными. Ознакомление учащихся со способами решения систем линейных уравнений с двумя переменными, с составлением системы линейных уравнений с двумя переменными по условию задачи.

2. Развивающая. Развитие мышления учащихся через умение выделять главное, развитие сознательного восприятия учебного материала, внимания и памяти.

3. Воспитательная. Содействие воспитанию культуры письменной и устной математической речи, графической культуры; формирование умения работать в парах, умения оценивать друг друга и давать себе самооценку.

Цель. Ход урока.

1. Мотивация

Системы уравнений, как и отдельные уравнения используются для решения сложных и необходимых задач. Ранее мы отмечали, что довольно часто реальной ситуации служит линейное уравнение с одной переменной или уравнение, которое после преобразований сводится к линейному.

1,2 слайд. Исаак Ньютон сказал: «Чтобы решить вопрос, относящийся к числам или к отвлеченным отношениям величин, нужно лишь перевести задачу с родного языка на алгебраический».

Сегодня нам предстоит сделать первые шаги в данном направлении.

Но для этого нам нужно вспомнить материал предыдущих тем.

2. Актуализация опорных знаний.

Как называется функция у=-2х+7?

Как определить, принадлежат ли точки А(-4;15), В(4,1) графику функции?

Что является графиком функции?

Сколько точек необходимо?

Построим график функции у=-х+2.

Без построения определите, будут ли пересекаться прямые? Как они могут располагаться?

Что называется уравнением? Что значит - решить уравнение? Решить уравнение 9х-7=6х+14. Сколько решений может иметь такое уравнение? ------

3. Знакомство с установкой и осознание нового материала.

Урок 1. Уравнение с двумя переменными. График линейного уравнения с двумя переменными.

Слайд 3-5.

Слайд 3. Работа с установкой. Что является решением линейного уравнения с двумя переменными? Найти решение уравнения х-3у=10. Как это удобнее сделать? Х=3у+10 Слайд 4

Проверим, какие из пар чисел (6;-4) , (2;1) являются решениями следующих уравнений х+у=2, х-у=10 . Слайд 5

График уравнения х+у=2 у нас уже есть, построим график х-у=10, определим координаты точки пересечения.

Урок 2. Системы линейных уравнений с двумя переменными. Графический способ решения. Способ подстановки.

Слайд 6-8

Как определить количество решений системы уравнений?

Определим алгоритм решения системы линейных уравнений с двумя переменными. Какую систему мы уже решили?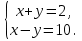

Слайд 9

Работа с установкой. В чем заключается способ подстановки?

Слайд 10

Решим систему способом подстановки.

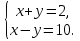
Слайд 11

Урок 3. Системы линейных уравнений с двумя переменными. Способ сложения. Решение задач составлением системы уравнений.

Работа с установкой. В чем заключается способ сложения?

Слайд 12

Решим систему способом сложения.

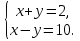
Урок 4,5. Многие задачи, в частности те, в которых нужно найти значение двух величин, удобно решать при помощи систем уравнений.

Слайд 13,14

4. Рефлексия. Осмысление результатов работы.

- Что нового узнали?

- Чему научились?

-Что показалось самым трудным?

Сегодня мы решили одну систему линейных уравнений с двумя переменными тремя способами. Следует обратить внимание на равноправие трёх способов решения систем. Преимуществом геометрического языка является его наглядность, зато алгебраический язык позволяет сводить задачу к точным вычислениям. На следующем уроке мы продолжим работать над темой и рассмотрим подробнее тему: «Уравнение с двумя переменными. График линейного уравнения с двумя переменными».

2 модуль.

Ход урока.

1. Закрепление и осознание знаний.

Самостоятельная работа с учебником. Работа в парах. Стр.217 отвечаем на вопросы по вариантам. Фронтальная работа. Стр.218 устные упражнения.

Решение упражнений у доски.

1. Определяем какая из пар является решением уравнения.

2. Выражаем одну переменную через другую.

3. Определяем принадлежность точки графику.

4. Строим график линейного уравнения с двумя переменными.

2. Подведение итогов урока.

На 22 грн купили несколько тетрадей по 5 грн и ручек по 3 грн. Сколько купили тетрадей и ручек? Решая задачу, количество тетрадей обозначь за х, а ручек за у. Составить уравнение по условию задачи. Назовите пару чисел, являющуюся решением этого уравнения.

3 модуль.

1. Закрепление знаний.

Решение упражнений у доски.

1. Построение в одной плоскости графиков двух уравнений. №1035

2. Составление уравнения, график которого пересекает оси координат в заданных точках. №1043

3. Самостоятельная работа с взаимопроверкой (обратная сторона доски).

А. Выразить переменную у через х. Пользуясь полученной формулой нати 2 решения. Х+у=12; у-х=10.

Б. Построить график уравнения, определив точки пересечения графика с координатными осями. 3Х+5у=15; 4у+3х=12.

В. Сколько решений имеет уравнение

(х-1)²+(у+2)²=0; (х+1)²+(у-2)²=0;

Каждое задание 4 балла.

2. Подведение итогов урока. Выставление оценок.