Рабочая программа по математике 9 класс УМК Ю.Г.Макарычев

РАБОЧАЯ ПРОГРАММА

Учителя муниципального бюджетного образовательного учреждения «Беркет-Ключёвская средняя общеобразовательная школа» Черемшанского муниципального района Республики Татарстан

Шамcутдиновой Кадрии Масхутовны

по математике

9 класс

Рассмотрено на заседании пед.совета

Протокол №______от «____»_____________2016 года.

2016-2017 учебный год.

Раздел 1.

Пояснительная записка.

Настоящая программа по математике для IX класса создана на основе:

- ФЗ - № 273 от 29.12.2012 «Об образовании в Российской Федерации»;

- Приказ МО и науки РФ от 5 марта2004 года № 1089 «Об утвержденииФедерального компонента государственных образовательных стандартов начального общего, основного общего и среднего(полного) общего образования» (с изменениями);

- Закон Республики Татарстан «Об Образовании» (в действующей редакции);

- Учебного плана МБОУ «Беркет-Ключевская СОШ» на 2016-2017 учебный год, утвержденного приказом №______от _____________2016 года;

- Примерные программы по учебным предметам. Программа для 5-11 классов татарской средней общеобразовательной школы, допущенной Министерством образования и науки РТ, под редакцией М.Г. Ахметзянова (Казань, «Магариф», 2009г.)

Примерная программа основного общего образования по математике и авторская программа по алгебре и геометрии взяты из «Программы общеобразовательных учреждений» АЛГЕБРА 7-9 классы, ГЕОМЕТРИЯ 7-9 классы, составитель: Бурмистрова Т.А издательство «Просвещение».

Рабочая программа рассчитана на 170 (102+68) часов (5 часа в неделю).

«Алгебра 9 класс» авторы Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.В. Суворова. Москва, «Просвещение» 2010г.

«Геометрия, 7 - 9» авторы Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. М.: Просвещение, 2009

- Законом РТ «Об образовании» (в действующей редакции);

Программа детализирует и раскрывает содержание стандарта, определяет общую стратегию обучения, воспитания и развития учащихся средствами учебного предмета в соответствии с целями изучения математики, которые определены стандартом.

Раздел 2.

Требования к уровню подготовки обучающихся.

Требования к результатам обучения направлены на реализацию деятельностного и личностно ориентированного подходов; освоение учащимися интеллектуальной и практической деятельности; овладение знаниями и умениями, востребованными в повседневной жизни, позволяющими ориентироваться в окружающем мире, значимыми для сохранения окружающей среды и собственного здоровья.

В результате изучения курса алгебры 9 класса обучающиеся должны:

знать/понимать

1. существо понятия математического доказательства; примеры доказательств;

2. существо понятия алгоритма; примеры алгоритмов;

3. как используются математические формулы, уравнения и неравенства; примеры их применения для решения математических и практических задач;

4. как математически определенные функции могут описывать реальные зависимости; приводить примеры такого описания;

5. как потребности практики привели математическую науку к необходимости расширения понятия числа;

6. вероятностный характер многих закономерностей окружающего мира; примеры статистических закономерностей и выводов;

7. каким образом геометрия возникла из практических задач землемерия; примеры геометрических объектов и утверждений о них, важных для практики;

8. смысл идеализации, позволяющей решать задачи реальной действительности математическими методами, примеры ошибок, возникающих при идеализации;

Алгебра

уметь

1. составлять буквенные выражения и формулы по условиям задач; осуществлять в выражениях и формулах числовые подстановки и выполнять соответствующие вычисления, осуществлять подстановку одного выражения в другое; выражать из формул одну переменную через остальные;

2. выполнять основные действия со степенями с целыми показателями, с многочленами и с алгебраическими дробями; выполнять разложение многочленов на множители; выполнять тождественные преобразования рациональных выражений;

3. применять свойства арифметических квадратных корней для вычисления значений и преобразований числовых выражений, содержащих квадратные корни;

4. решать линейные, квадратные уравнения и рациональные уравнения, сводящиеся к ним, системы двух линейных уравнений и несложные нелинейные системы;

5. решать линейные и квадратные неравенства с одной переменной и их системы;

6. решать текстовые задачи алгебраическим методом, интерпретировать полученный результат, проводить отбор решений, исходя из формулировки задачи;

7. изображать числа точками на координатной прямой;

8. определять координаты точки плоскости, строить точки с заданными координатами; изображать множество решений линейного неравенства;

9. распознавать арифметические и геометрические прогрессии; решать задачи с применением формулы общего члена и суммы нескольких первых членов;

10. находить значения функции, заданной формулой, таблицей, графиком по ее аргументу; находить значение аргумента по значению функции, заданной графиком или таблицей;

11. определять свойства функции по ее графику; применять графические представления при решении уравнений, систем, неравенств;

12. описывать свойства изученных функций (у=кх, где к0, у=кх+b, у=х2, у=х3, у =, у=, у=ах2+bх+с, у= ах2+n у= а(х - m) 2 ), строить их графики;

использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:

13. выполнения расчетов по формулам, составления формул, выражающих зависимости между реальными величинами; нахождения нужной формулы в справочных материалах;

14. моделирования практических ситуаций и исследований построенных моделей с использованием аппарата алгебры;

15. описания зависимостей между физическими величинами соответствующими формулами при исследовании несложных практических ситуаций;

16. интерпретации графиков реальных зависимостей между величинами;

Элементы логики, комбинаторики, статистики и теории вероятностей

уметь

17. проводить несложные доказательства, получать простейшие следствия из известных или ранее полученных утверждений, оценивать логическую правильность рассуждений, использовать примеры для иллюстрации и контрпримеры для опровержения утверждений;

18. извлекать информацию, представленную в таблицах, на диаграммах, графиках; составлять таблицы, строить диаграммы и графики;

19. решать комбинаторные задачи путем систематического перебора возможных вариантов, а также с использованием правила умножения;

20. вычислять средние значения результатов измерений;

21. находить частоту события, используя собственные наблюдения и готовые статистические данные;

22. находить вероятности случайных событий в простейших случаях;

использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:

23. выстраивания аргументации при доказательстве (в форме монолога и диалога);

24. распознавания логически некорректных рассуждений;

25. записи математических утверждений, доказательств;

26. анализа реальных числовых данных, представленных в виде диаграмм, графиков, таблиц;

27. решения практических задач в повседневной и профессиональной деятельности с использованием действий с числами, процентов, длин, площадей, объемов, времени, скорости;

28. решения учебных и практических задач, требующих систематического перебора вариантов;

29. сравнения шансов наступления случайных событий, оценки вероятности случайного события в практических ситуациях, сопоставления модели с реальной ситуацией;

30. понимания статистических утверждений.

Геометрия

уметь

1. пользоваться языком геометрии для описания предметов окружающего мира;

2. распознавать геометрические фигуры, различать их взаимное расположение;

3. изображать геометрические фигуры; выполнять чертежи по условию задач; осуществлять преобразования фигур;

4. распознавать на чертежах, моделях и в окружающей обстановке основные пространственные тела, изображать их;

5. в простейших случаях строить сечения и развертки пространственных тел;

6. проводить операции над векторами, вычислять длину и координаты вектора, угол между векторами;

7. вычислять значения геометрических величин (длин, углов, площадей, объемов), в том числе: для углов от 0 до 180° определять значения тригонометрических функций по заданным значениям углов; находить значения тригонометрических функций по значению одной из них, находить стороны, углы и площади треугольников, длины ломаных, дуг окружности, площадей основных геометрических фигур и фигур, составленных из них;

8. решать геометрические задачи, опираясь на изученные свойства фигур и отношений между ними, применяя дополнительные построения, алгебраический и тригонометрический аппарат, идеи симметрии;

9. проводить доказательные рассуждения при решении задач, используя известные теоремы, обнаруживая возможности для их использования;

10. решать простейшие планиметрические задачи в пространстве;

использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:

11. описания реальных ситуаций на языке геометрии;

12. расчетов, включающих простейшие тригонометрические формулы;

13. решения геометрических задач с использованием тригонометрии

14. решения практических задач, связанных с нахождением геометрических величин (используя при необходимости справочники и технические средства);

15. построений геометрическими инструментами (линейка, угольник, циркуль, транспортир).

Раздел 3.

Содержание учебного предмета.

Линейные и квадратные неравенства (повторение).

Рациональное неравенство. Метод интервалов.

Множества и операции над ними.

Система неравенств. Решение системы неравенств.

Функция. Независимая переменная. Зависимая переменная. Область определения функции. Естественная область определе­ния функции. Область значений функции.

Способы задания функции (аналитический, графический, табличный, словесный).

Свойства функций (монотонность, ограниченность, выпук­лость, наибольшее и наименьшее значения, непрерывность). Исследование функций: у = С, у = kx + т, у = kx², у = ах² + bх + с.

Четные и нечетные функции. Алгоритм исследования функ­ции на четность. Графики четной и нечетной функций.

Степенная функция с натуральным показателем, ее свойства и график. Степенная функция с отрицательным целым показате­лем, ее свойства и график.

(27ч)

Векторы

Понятие вектора. Равенство векторов. Сложение и вычитание векторов. Умножение вектора на число. Разложение вектора по двум неколлинеарным векторам. Координаты вектора. Простей­шие задачи в координатах. Уравнения окружности и прямой. Применение векторов и координат при решении задач.

(14 ч)

Уравнения и неравенства с одной переменной

Целые уравнения. Уравнение с двумя переменными и его график. Системы уравнений второй степени. Решение задач с помощью систем уравнений второй степени.

(14 ч)

Соотношения между сторонами и углами треугольника. Скалярное произведение векторов

Синус, косинус и тангенс угла. Теоремы синусов и косинусов. Решение треугольников. Скалярное произведение векторов и его применение в геометрических

(11 ч)

Уравнения и неравенства с двумя переменными

Уравнение с двумя переменными и его график. Системы уравнений второй степени. Решение задач с помощью систем уравнений второй степени. Неравенства с двумя переменными и их системы. Графическая интерпретация уравнений с двумя переменными и их систем, неравенств с двумя переменными и их систем.

(17 ч)

Длина окружности и площадь круга

Правильные многоугольники. Окружности, описанная около правильного многоугольника и вписанная в него. Построение правильных многоугольников. Длина окружности. Площадь круга.

(12 час.)

Арифметическая и геометрическая прогрессии

Арифметическая и геометрическая прогрессии. Формулы n-го члена и суммы первых nчленов прогрессии. Бесконечно убывающая геометрическая прогрессия.

(15 ч)

Движения

Отображение плоскости на себя. Понятие движения. Осевая и центральная симметрии. Параллельный перенос. Поворот. На­ложения и движения.

(7 ч)

Элементы комбинаторики и теории вероятностей

Комбинаторное правило умножения. Перестановки, размещения, сочетания. Относительная частота и вероятность случайного события.

(13 ч)

Начальные сведения из стереометрии

Предмет стереометрии. Геометрические тела и поверхности. Многогранники: призма, параллелепипед, пирамида, формулы для вычисления их объемов. Тела и поверхности вращения: цилиндр, конус, сфера, шар, формулы для вычисления их объемов

(8 ч)

Итоговое повторение

(25 ч)

Раздел 4.

Календарно-тематическое планирование ФК ГОС.

УМК Ю.Н.Макарычев, Н.Г. Миндюк, 2014 г, Москва «Просвещение»

п/п

Изучаемый раздел, тема урока

Количество часов

Календарные сроки

планируемые

фактические

Квадратичная функция (22ч)

Цель: расширить сведения о свойствах функций, ознакомить учащихся со свойствами и графиком квадратичной функции

1-

5

Повторение. Тождественные преобразования. Степень с целым показателем. Решение уравнений. Решение неравенств. Вводный контроль.

5

2- 8.09

§ 1. Функции и их свойства (5)

6

Функция. Область определения и область значений функции

1

9.09

7

Функция. Область определения и область значений функции

1

13.09

8

Свойства функций

1

14.09

9

Свойства функций

1

15.09

10

Свойства функций

1

16.09

§ 2. Квадратный трехчлен (6)

11

Квадратный трёхчлен и его корни

1

19.09

12

Квадратный трёхчлен и его корни

1

20.09

13

Разложение квадратного трёхчлена на множители

1

21.09

14

Разложение квадратного трёхчлена на множители

1

22.09

15

Разложение квадратного трёхчлена на множители. Проверочная самостоятельная работа

1

23.09

16

Контрольная работа №1 по теме: «Функции и их свойства. Квадратный трехчлен»

1

26.09

§ 3. Квадратичная функция и ее график (7)

17

График функции у=ах²

1

27.09

18

График функции у=ах²

1

28.09

19

Графики функций у=ах²+n, у=а(x - m)²

1

29.09

20

Графики функций у=ах²+n, у=а(x-m)²

1

30.09

21

Построение графика квадратичной функции

1

3.10

22

Построение графика квадратичной функции

1

4.10

23

Построение графика квадратичной функции

1

5.10

§ 4. Степенная функция. Корень n - й степени (3 + 1ч. к/р)

24

Функция у=хⁿ

1

6.10

25

Корень n-й степени

1

7.10

26

Степень с рациональным показателем

1

10.10

27

Контрольная работа № 2: «Квадратичная функция. Степенная функция»

1

11.10

Векторы. Метод координат. (14)

Цель: научить учащихся выполнять действия над векторами как направленными отрезками, что важно для применения векторов в физике; познакомить с использованием векторов и метода координат при решении геометрических задач

§ 1. Понятие вектора (1)

28

Понятие вектора. Равенство векторов.

Откладывание вектора от данной точки.

1

12.10

§ 2. Сложение и вычитание векторов. (2)

29

Сумма двух векторов. Сумма нескольких векторов. Вычитание векторов

1

13.10

30

Решение задач по теме: «Сложение и вычитание векторов»

1

14.10

§ 3. Умножение вектора на число. Применение векторов к решению задач. (2)

31

Умножение вектора на число

1

17.10

32

Применение векторов к решению задач. Средняя линия трапеции

1

18.10

§ 1. Координаты вектора (2)

33

Разложение вектора по двум неколлинеарным векторам

1

19.10

34

Координаты вектора

1

20.10

§ 2. Простейшие задачи в координатах (2)

35

Простейшие задачи в координатах

1

21.10

36

Простейшие задачи в координатах

1

24.10

§ 3. Уравнение окружности и прямой (5)

37

Уравнение окружности

1

25.10

38

Уравнение прямой

1

26.10

39

Уравнение окружности и прямой. Решение задач.

1

27.10

40

Решение задач по теме: «Метод координат»

1

28.10

41

Контрольная работа № 3 «Метод координат»

1

7.11

Уравнения и неравенства с одной переменной (14ч)

Цель: систематизировать и обобщить сведения о решении целых и дробных рациональных уравнений с одной переменной, сформировать умение решать неравенства вида ax²+bx+c>0, ax²+bx+c<0, где a≠0.

§ 5. Уравнения с одной переменной (8 + 1 ч. К/р.)

42

Целое уравнение и его корни

1

8.11

43

Уравнения, приводимые к квадратным

1

9.11

44

Уравнения, приводимые к квадратным

1

10.11

45

Дробные рациональные уравнения

1

11.11

46

Дробные рациональные уравнения

1

14.11

47

Дробные рациональные уравнения

1

15.11

48

Дробные рациональные уравнения

1

16.11

49

Контрольная работа №4 по теме: « Уравнения с одной переменной»

1

17.11

§ 6. Неравенства с одной переменной (5 + 1ч. к/р)

50

Решение неравенств второй степени с одной переменной

1

18.11

51

Решение неравенств второй степени с одной переменной

1

21.11

52

Решение неравенств методом интервалов

1

22.11

53

Решение неравенств методом интервалов

1

23.11

54

Обобщающий урок «Уравнения и неравенства с одной переменной»

1

24.11

55

Контрольная работа №5 по теме: « Неравенства с одной переменной»

1

25.11

Соотношения между сторонами и углами треугольника. Скалярное произведение векторов. (11)

Цель: развить умение учащихся применять тригонометрический аппарат при решении геометрических задач.

§ 1. Синус, косинус, тангенс угла (3)

56

Синус, косинус и тангенс угла

1

28.11

57

Основное тригонометрическое тождество. Формулы приведения.

1

29.11

58

Формулы для вычисления координат точки

1

30.11

§ 2. Соотношения между сторонами и углами треугольника (4)

59

Теорема о площади треугольника

1

1.12

60

Теоремы синусов и косинусов

1

2.12

61

Решение треугольников

1

5.12

62

Измерительные работы

1

6.12

§ 3. Скалярное произведение векторов (2 + 1ч р/з +1ч к/р)

63

Скалярное произведение векторов

1

7.12

64

Скалярное произведение в координатах

1

8.12

65

Применение скалярного произведения векторов при решении задач

1

9.12

66

Контрольная работа № 6 «Соотношения в треугольнике. Скалярное произведение векторов»

1

12.12

Уравнения и неравенства с двумя переменными (17ч)

Цель: выработать умение решать простейшие системы, содержащие уравнение второй степени с двумя переменными, и текстовые задачи с помощью составления таких систем.

§ 7. Уравнения с двумя переменными и их системы (12)

67

Уравнение с двумя переменными и его график

1

13.12

68

Уравнение с двумя переменными и его график

1

14.12

69

Графический способ решения систем уравнений

1

15.12

70

Графический способ решения систем уравнений

1

16.12

71

Графический способ решения систем уравнений

1

19.12

72

Решение систем уравнений второй степени

1

20.12

73

Решение систем уравнений второй степени

1

21.12

74

Решение систем уравнений второй степени

1

22.12

75

Решение задач с помощью систем уравнений второй степени

1

23.12

76

Решение задач с помощью систем уравнений второй степени

1

9.01

77

Решение задач с помощью систем уравнений второй степени

1

10.01

78

Решение задач с помощью систем уравнений второй степени

1

11.01

§ 8. Неравенства с двумя переменными и их системы (4 + 1ч. к/р)

79

Неравенства с двумя переменными

1

12.01

80

Неравенства с двумя переменными

1

13.01

81

Системы неравенств с двумя переменными

1

16.01

82

Системы неравенств с двумя переменными

1

17.01

83

Контрольная работа № 7 по теме: «Уравнения и неравенства с двумя переменными»

1

18.01

Длина окружности и площадь круга. (12)

Цель: расширить знание учащихся о многоугольниках; рассмотреть понятия длины окружности и площади круга и формулы для их вычисления

§ 1. Правильные многоугольники (4)

84

Правильный многоугольник

1

19.01

85

Окружность, описанная около правильного многоугольника и вписанная в правильный многоугольник

1

20.01

86

Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной окружности

1

23.01

87

Решение задач по теме: «Правильный многоугольник»

1

24.01

§ 2. Длина окружности и площадь круга (4 + 3ч. р/з + 1ч. к/р)

88

Длина окружности

1

25.01

89

Длина окружности. Решение задач

1

26.01

90

Площадь круга и кругового сектора

1

27.01

91

Площадь круга и кругового сектора. Решение задач

1

30.01

92

Обобщение по теме: «Длина окружности. Площадь круга»

1

31.01

93

Решение задач по теме: «Длина окружности и площадь круга»

1

1.02

94

Подготовка к контрольной работе

1

2.02

95

Контрольная работа № 8 по теме: «Длина окружности и площадь круга»

1

3.02

Арифметическая и геометрическая прогрессии (15ч)

Цель: дать понятие об арифметической и геометрической прогрессиях как числовых последовательностях особого вида.

§ 9. Арифметическая прогрессия (7 + 1ч. к/р))

96

Последовательности

1

6.02

97

Последовательности

1

7.02

98

Определение арифметической прогрессии. Формула п-го члена арифметической прогрессии

1

8.02

99

Определение арифметической прогрессии. Формула п-го члена арифметической прогрессии

1

9.02

100

Формула суммы п первых членов арифметической прогрессии

1

10.02

101

Формула суммы п первых членов арифметической прогрессии

1

13.02

102

Формула суммы п первых членов арифметической прогрессии

1

14.02

103

Контрольная работа № 9 по теме: « Арифметическая прогрессия»

1

15.02

§ 10. Геометрическая прогрессия(6 +1ч к/р)

104

Определение геометрической прогрессии. Формула п - го члена геометрической прогрессии

1

16.02

105

Определение геометрической прогрессии. Формула п - го члена геометрической прогрессии

1

17.02

106

Формула суммы п первых членов геометрической прогрессии

1

20.02

107

Формула суммы п первых членов геометрической прогрессии

1

21.02

108

Формула суммы п первых членов геометрической прогрессии

1

22.02

109

Формула суммы п первых членов геометрической прогрессии

1

24.02

110

Контрольная работа № 10 по теме: «Геометрическая прогрессия»

1

27.02

Движения (7ч)

Цель: познакомить учащихся с понятием движения и его свойствами, с основными видами движений, со взаимоотношениями наложений и движений.

§ 1. Понятие движения (3)

111

Понятие движения

1

28.02

112

Свойства движений

1

1.03

113

Решение задач по теме «Понятие движения. Осевая и центральная симметрии»

1

2.03

§ 2. Параллельный перенос и поворот (3 +1ч к/р)

114

Параллельный перенос

1

3.03

115

Поворот

1

6.03

116

Решение задач по теме: «Параллельный перенос. Поворот» Решение задач по теме: «Движения»

1

7.03

117

Контрольная работа № 11 «Движения»

1

9.03

Элементы комбинаторики и теории вероятностей (13ч)

Цель: ознакомить учащихся с понятиями перестановки, размещения, сочетания и соответствующими формулами для подсчета их числа; ввести понятия относительной частоты и вероятности случайного события.

§ 11. Элементы комбинаторики (9)

118

Примеры комбинаторных задач

1

10.03

119

Примеры комбинаторных задач

1

13.03

120

Перестановки

1

14.03

121

Перестановки

1

15.03

122

Размещения

1

16.03

123

Размещения

1

17.03

124

Сочетания

1

29.03

125

Сочетания

1

30.03

126

Решение комбинаторных задач

1

31.03

§ 12. Начальные сведения из теории вероятностей (3ч + 1ч.к/р)

127

Относительная частота случайного события

1

3.04

128

Вероятность равновозможных событий

1

4.04

129

Решение задач по теории вероятностей

1

5.04

130

Контрольная работа №12 по теме: «Комбинаторика и теория вероятностей»

1

6.04

Начальные сведения из стереометрии.(8ч).Об аксиомах планиметрии.(2ч)

Цель: дать начальное представление о телах и поверхностях в пространстве; познакомить учащихся с основными формулами для вычисления площадей поверхностей и объемов тел; дать более глубокое представление о системе аксиом планиметрии и аксиоматическом методе

§ 1. Многогранники (4)

131

Предмет стереометрии. Многогранник

1

7.04

132

Призма. Параллелепипед.

1

10.04

133

Объем тела. Свойства прямоугольного параллелепипеда

1

11.04

134

Пирамида. Решение задач

1

12.04

§ 2. Тела и поверхности вращения (4)

135

Цилиндр

1

13.04

136

Конус

1

14.04

137

Сфера и шар

1

17.04

138

Решение задач. Тела и поверхности вращения

1

18.04

139

Об аксиомах планиметрии

1

19.04

140

Об аксиомах планиметрии

1

20.04

Итоговое повторение. (25ч)

Цель: систематизировать теоретические знания учащихся за курс математики 9 класса

141

142

Графики функций

2

21.04

24.04

143-144

Уравнения, неравенства, системы

2

25.04

26.04

145-146

Арифметическая и геометрическая прогрессии

2

27.04

28.04

147-148

Элементы комбинаторики и теории вероятностей

2

2.05

3.05

149-150

Текстовые задачи.

2

4.05

5.05

151

Повторение по теме «Начальные геометрические сведения. Параллельные прямые»

1

8.05

152

Треугольники

1

9.05

153

Треугольники

1

10.05

154

Окружность

1

11.05

155-156

Четырехугольники. Многоугольники

2

12.05

157

Векторы. Метод координат. Движения

1

15.05

158

Векторы

1

16.05

159

Контрольная работа № 13. Итоговая работа

1

17.05

160-170

Комплексное повторение основных вопросов курса алгебры. Решение тренировочных заданий (подготовка к ОГЭ)

11

18.05-25.05

Приложение:

Контрольные работы.

АлгебраК-1

Вариант 1.

1. Дана функция . При каких значениях аргумента ? Является ли эта функция возрастающей или убывающей?

2. Разложите на множители квадратный трехчлен:

а) ; б) .

3. Сократите дробь .

4. Область определения функции g - отрезок . Найдите нули функции, промежутки возрастания и убывания, область значений функции.

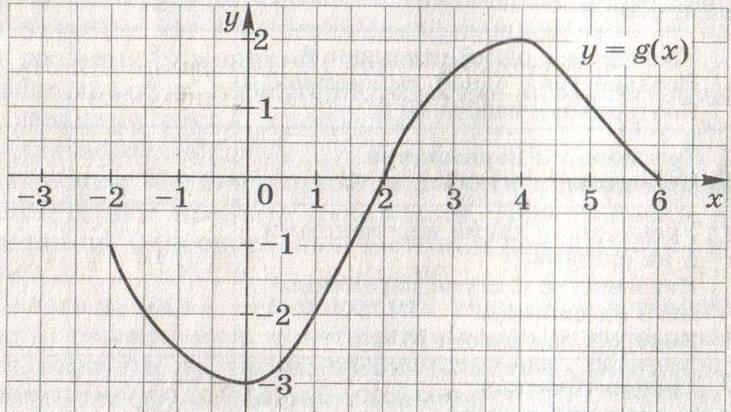
5. Сумма положительных чисел а и b равна 50. При каких значениях а и b их произведение будет наибольшим?

К-1

Вариант 2.

1. Дана функция . При каких значениях аргумента ? Является ли эта функция возрастающей или убывающей?

2. Разложите на множители квадратный трехчлен:

а) ; б) .

3. Сократите дробь .

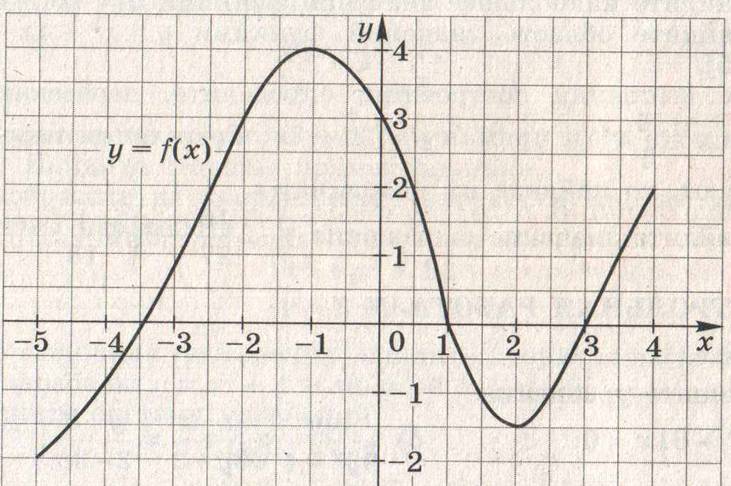
4. Область определения функции f - отрезок . Найдите нули функции, промежутки возрастания и убывания, область значений функции.

5. Сумма положительных чисел с и d равна 70. При каких значениях c и d их произведение будет наибольшим?

К-2

Вариант 1.

1. Постройте график функции . Найдите с помощью графика:

а) значение у при х = 0,5;

б) значения х, при которых у = - 1;

в) нули функции; промежутки, в которых

y > 0 и в которых y < 0;

г) промежуток, на котором функция возрастает.

2. Найдите наименьшее значение функции .

3. Найдите область значений функции , где .

4. Не выполняя построения, определите, пересекаются ли парабола и прямая . Если точки пересечения существуют, то найдите их координаты.

5. Найдите значение выражения

К-2

Вариант 2.

1. Постройте график функции . Найдите с помощью графика:

а) значение у при х = 1,5;

б) значения х, при которых у = 2;

в) нули функции; промежутки, в которых

y > 0 и в которых y < 0;

г) промежуток, на котором функция убывает.

2. Найдите наибольшее значение функции .

3. Найдите область значений функции , где .

4. Не выполняя построения, определите, пересекаются ли парабола и прямая . Если точки пересечения существуют, то найдите их координаты.

5. Найдите значение выражения

К-3

Вариант 1.

1. Решите уравнение:

а) ;

б) .

2. Решите неравенство:

а) ; б) .

3. Решите неравенство методом интервалов:

а) ; б) .

4. Решите биквадратное уравнение

.

5. При каких значениях т уравнение имеет два корня?

6. Найдите область определения функции

.

7. Найдите координаты точек пересечения графиков функций и .

К-3

Вариант 2.

1. Решите уравнение:

а) ; б) .

2. Решите неравенство:

а) ; б) .

3. Решите неравенство методом интервалов:

а) ; б) .

4. Решите биквадратное уравнение

.

5. При каких значениях п уравнение не имеет корней?

6. Найдите область определения функции

.

7. Найдите координаты точек пересечения графиков функций и .

К-4

Вариант 1.

1. Решите систему уравнений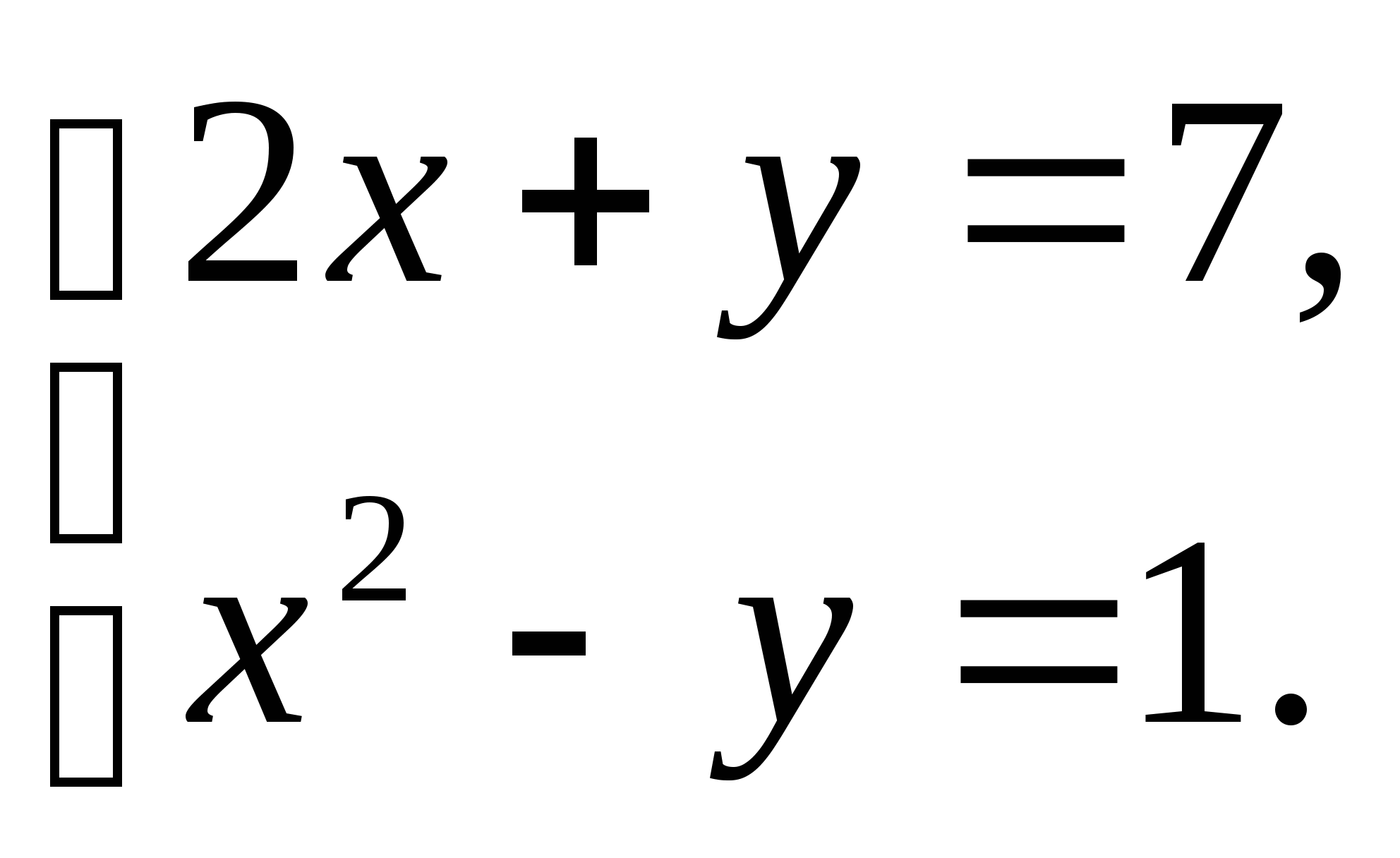

2. Периметр прямоугольника равен 28 м, а его площадь равна 40 м². Найдите стороны прямоугольника.

3. Изобразите на координатной плоскости множество решений системы неравенств

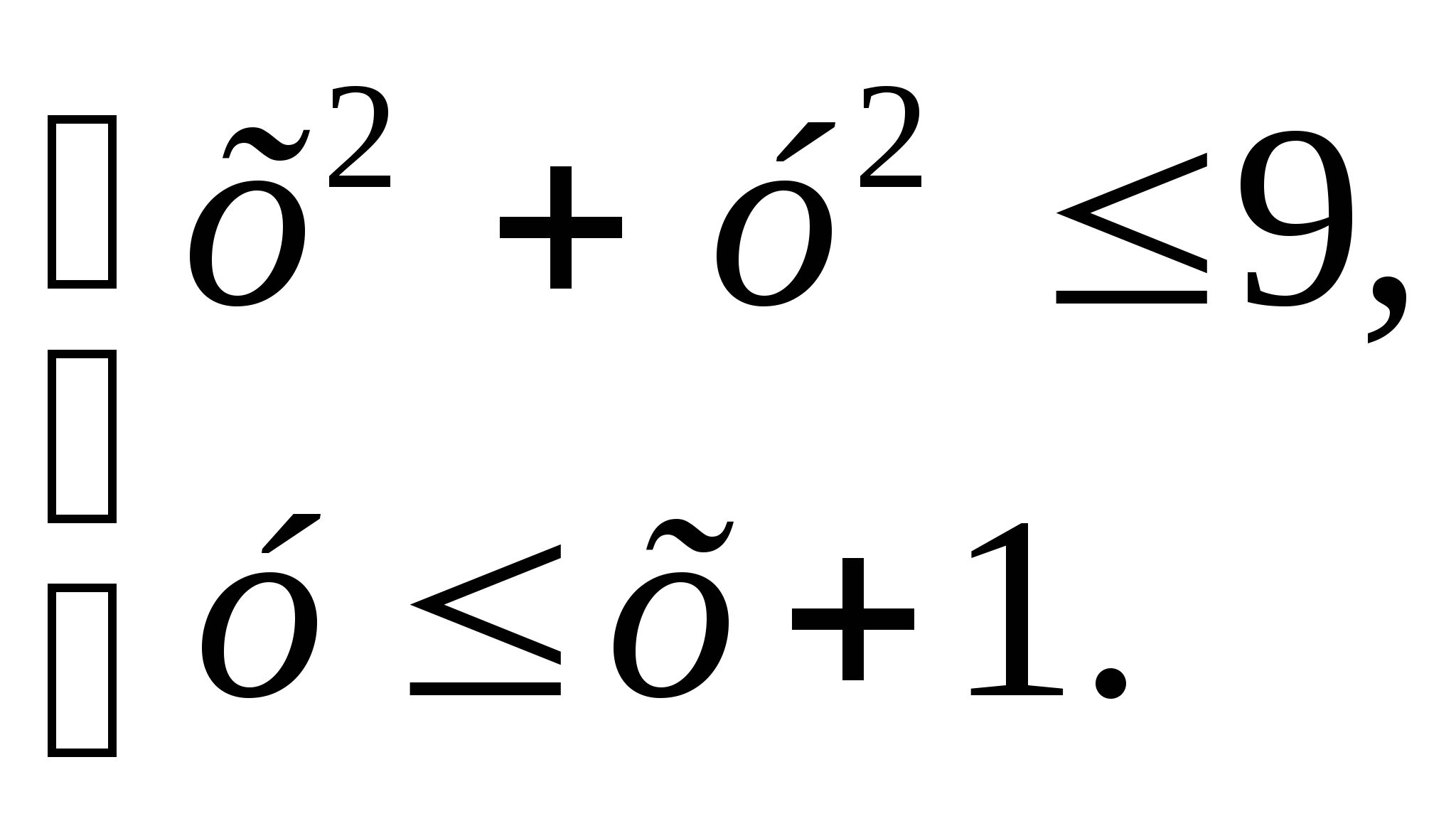
4. Не выполняя построения, найдите координаты точек пересечения параболы и прямой .

5. Решите систему уравнений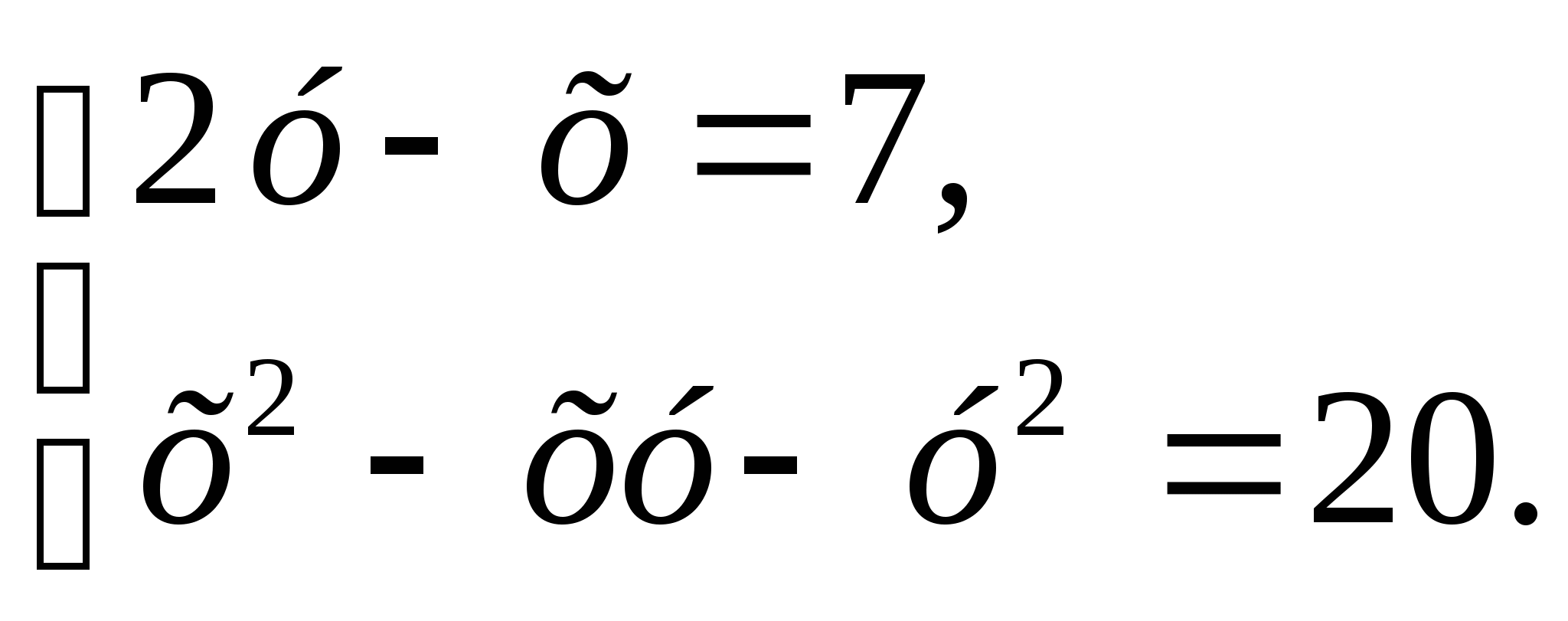

К-4

Вариант 2.

1. Решите систему уравнений

2. Одна из сторон прямоугольника на 2 см больше другой стороны. Найдите стороны прямоугольника, если его площадь равна 120см².

3. Изобразите на координатной плоскости множество решений системы неравенств

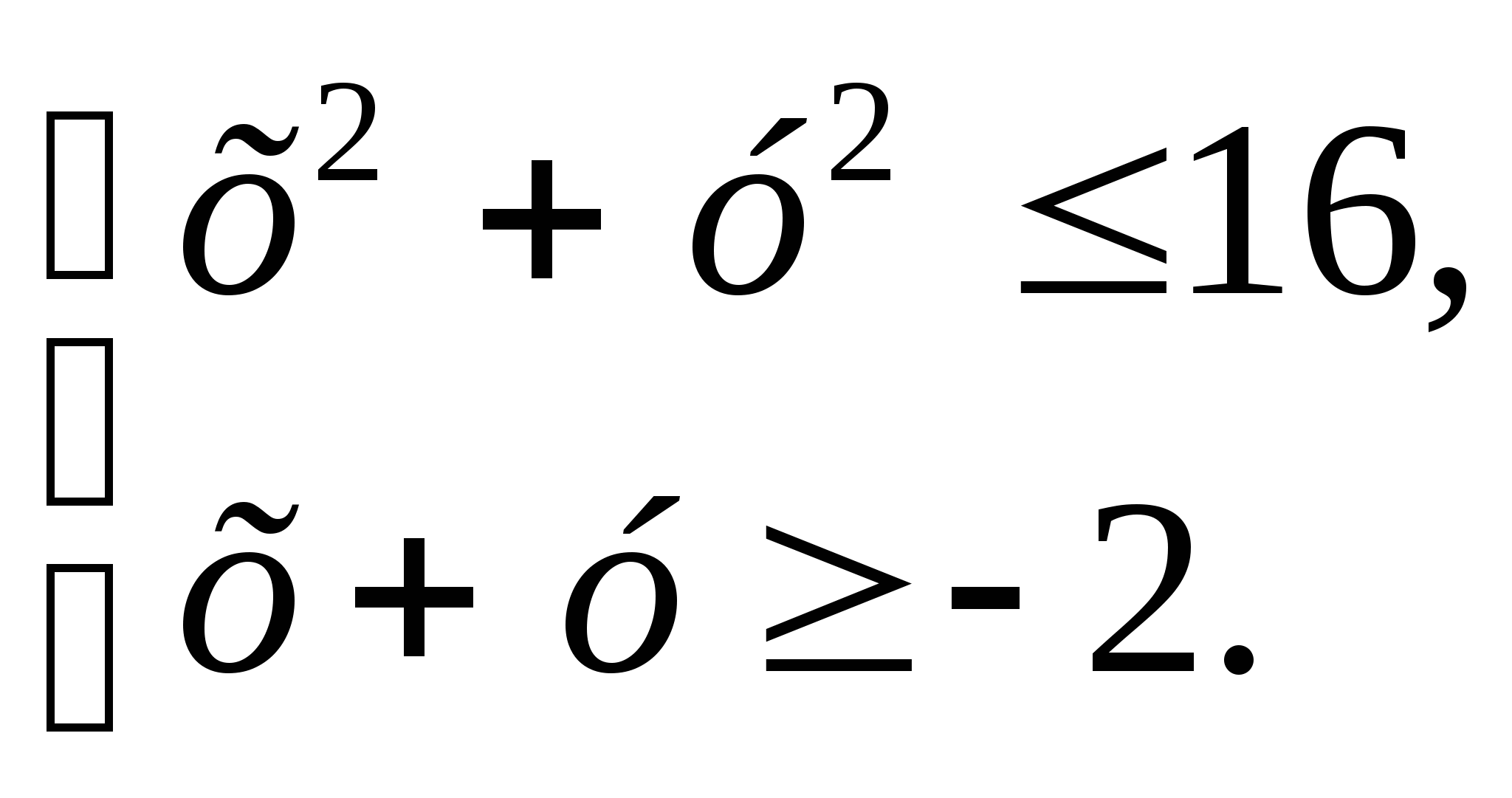
4. Не выполняя построения, найдите координаты точек пересечения окружности и прямой .

5. Решите систему уравнений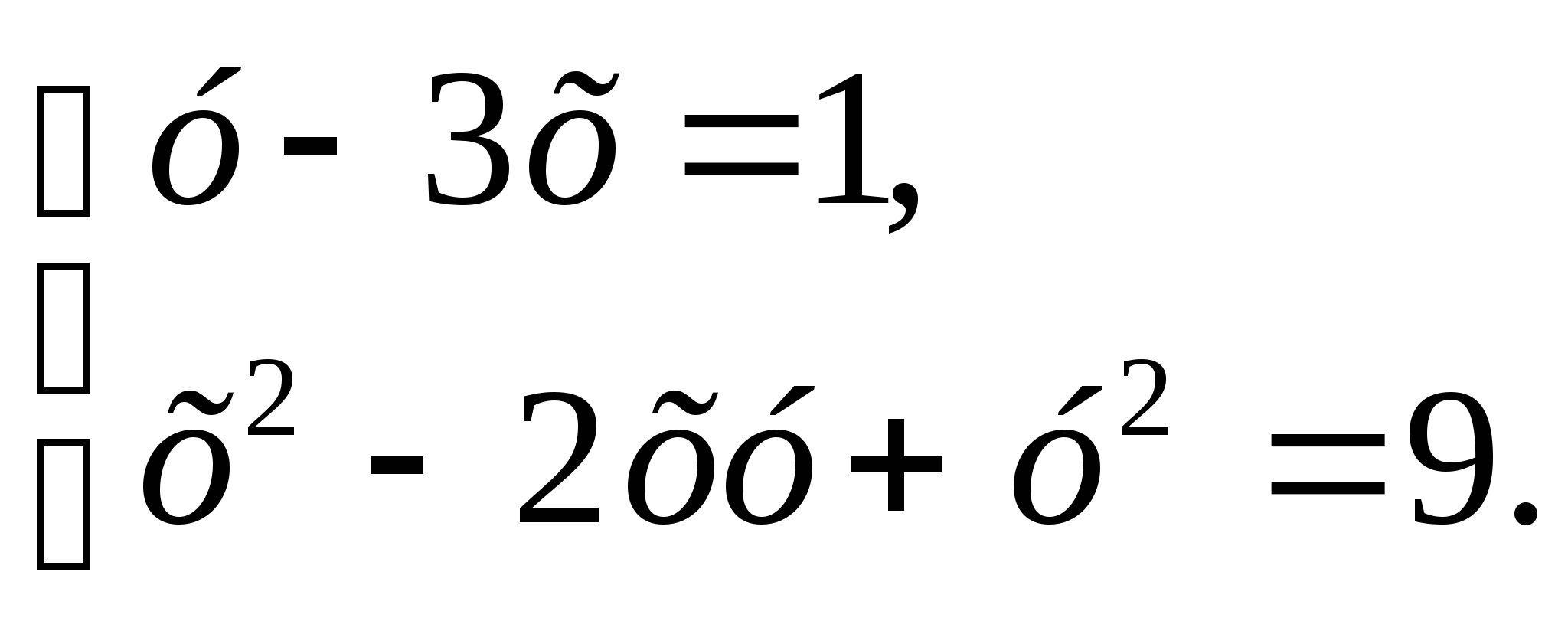

К-5

Вариант 1.

1. Найдите двадцать третий член арифметической прогрессии , если и .

2. Найдите сумму шестнадцати первых членов арифметической прогрессии: 8; 4; 0; … .

3. Найдите сумму шестидесяти первых членов последовательности , заданной формулой .

4. Является ли число 54,5 членом арифметической прогрессии , в которой и ?

5. Найдите сумму всех натуральных чисел, кратных 3 и не превосходящих 100.

К-5

Вариант 2.

1. Найдите восемнадцатый член арифметической прогрессии , если и .

2. Найдите сумму двадцати первых членов арифметической прогрессии: - 21; - 18; - 15; … .

3. Найдите сумму сорока первых членов последовательности , заданной формулой .

4. Является ли число 30,4 членом арифметической прогрессии , в которой и ?

5. Найдите сумму всех натуральных чисел, кратных 7 и не превосходящих 150.

К-6

Вариант 1.

1. Найдите седьмой член геометрической прогрессии , если и .

2. Первый член геометрической прогрессии равен 2, а знаменатель равен 3. Найдите сумму шести первых членов этой прогрессии.

3. Найдите сумму бесконечной геометрической прогрессии: 24; -12; 6; … .

4. Найдите сумму девяти первых членов геометрической прогрессии с положительными членами, зная, что и .

К-6

Вариант 2.

1. Найдите шестой член геометрической прогрессии , если и .

2. Первый член геометрической прогрессии равен 6, а знаменатель равен 2. Найдите сумму семи первых членов этой прогрессии.

3. Найдите сумму бесконечной геометрической прогрессии: - 40; 20; - 10; … .

4. Найдите сумму восьми первых членов геометрической прогрессии с положительными членами, зная, что и .

К-7

Вариант 1.

1. Сколькими способами могут разместиться 5 человек в салоне автобуса на 5 свободных местах?

2. Сколько трехзначных чисел, в которых нет одинаковых цифр, можно составить из цифр 1, 2, 5, 7, 9?

3. Победителю конкурса книголюбов разрешается выбрать две книги из 10 различных книг. Сколькими способами он может осуществить этот выбор?

4. В доме 90 квартир, которые распределяются по жребию. Какова вероятность того, что жильцу не достанется квартира на первом этаже, если таких квартир 6?

5. Из 8 мальчиков и 5 девочек надо выделить для работы на пришкольном участке 3 мальчиков и 2 девочек. Сколькими способами это можно сделать?

6. На четырех карточках записаны цифры 1, 3, 5, 7. Карточки перевернули и перемешали. Затем наугад последовательно положили эти карточки в ряд одну за другой и открыли. Какова вероятность того, что в результате получится число 3157?

К-7

Вариант 2.

1. Сколько шестизначных чисел можно составить из цифр 1, 2, 3, 5, 7, 9 без повторений цифр?

2. Из 8 учащихся класса, успешно выступивших на школьной олимпиаде, надо выбрать двух для участия в городской олимпиаде. Сколькими способами можно сделать этот выбор?

3. Из 15 туристов надо выбрать дежурного и его помощника. Какими способами это можно сделать?

4. Из 30 книг, стоящих на полке, 5 учебников, а остальные художественные произведения. Наугад берут с полки одну книгу. Какова вероятность того, что она не окажется учебником?

5. Из 9 книг и 6 журналов надо выбрать 2 книги и 3 журнала. Сколькими способами можно сделать этот выбор?

6. На пяти карточках написаны буквы а, в, и, л, с. Карточки перевернули и перемешали. Затем наугад последовательно положили эти карточки в ряд одну за другой и открыли. Какова вероятность того, что в результате получится слово «слива»?

ИТОГОВАЯ КОНТРОЛЬНАЯ РАБОТА

Вариант 1.

1. Упростите выражение .

2. Решите систему уравнений

3. Решите неравенство .

4. Представьте выражение в виде степени с основанием а.

5. Постройте график функции . Укажите, при каких значениях х функция принимает положительные значения.

6. В фермерском хозяйстве под гречиху было отведено два участка. С первого участка собрали 105 ц гречихи, а со второго, площадь которого на 3 га больше, собрали 152 ц. Найдите площадь каждого участка, если известно, что урожайность гречихи на первом участке была на 2 ц с 1 га больше, чем на

втором.

ИТОГОВАЯ КОНТРОЛЬНАЯ РАБОТА

Вариант 2.

1. Упростите выражение .

2. Решите систему уравнений

3. Решите неравенство .

4. Представьте выражение в виде степени с основанием у.

5. Постройте график функции . Укажите, при каких значениях х функция принимает отрицательные значения.

6. Из пункта А в пункт В, расстояние между которыми 45 км, выехал велосипедист. Через 30 мин вслед за ним выехал второй велосипедист, который прибыл в пункт В на 15 мин раньше первого. Какова скорость первого велосипедиста, если она на 3 км/ч меньше скорости второго?

ГеометрияКР №1.

Вариант №1.

1. Найдите координаты и длину вектора 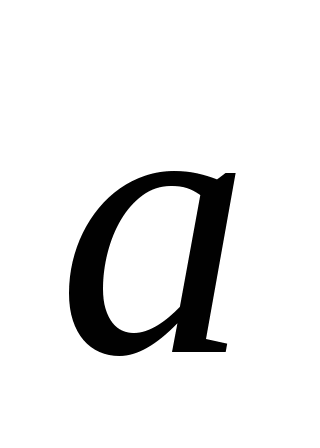, если = - + , =, =,

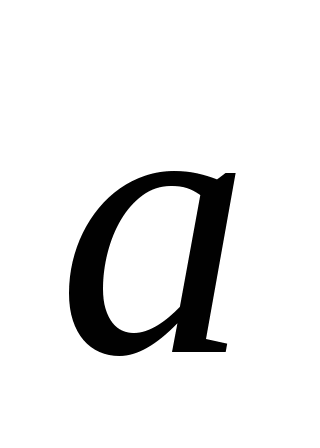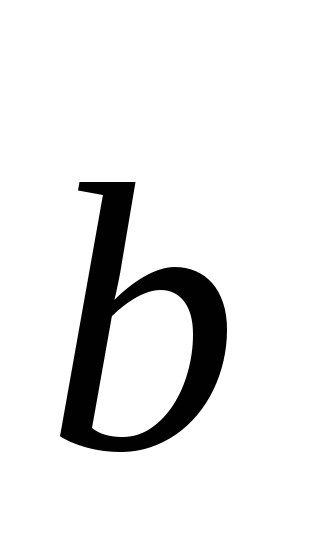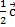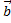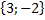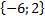2. Даны координаты вершин треугольника АВС: А(-6;1),В(2;4), С(2;-2). Докажите, что треугольник АВС равнобедренный, и найдите высоту треугольника, проведенную из вершины А.

3. Окружность задана уравнением

(х-1)²+y²=9. Напишите уравнение прямой, проходящей через ее центр и параллельной оси ординат.

КР №1.

Вариант №2.

4. Найдите координаты и длину вектора 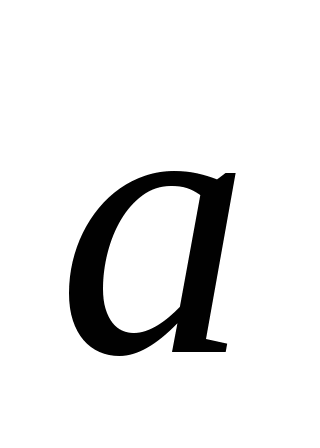, если = , =, =,

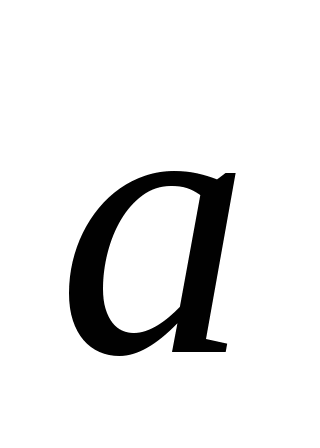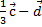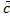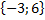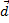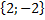5. Даны координаты вершин четырехугольника АВСD: А(-6;1), В(0;5), С(6;-4), D(0;-8). Докажите, что АВСD прямоугольник, и найдите координаты точки пересечения его диагоналей.

6. Окружность задана уравнением

(х+1)²+(y-2)²16. Напишите уравнение прямой, проходящей через ее центр и параллельной оси абсцисс.

КР №2.

Вариант №1.

1.Найдите угол между лучом ОА и положительной полуосью ОХ, если А(-1;3).

2.Решите треугольник АВС, если В=30⁰, С=105⁰, ВС=3см.

3.Найдите косинус угла М треугольника KLM, если К(1;7), L(-2;4), М(2;0).

КР №2.

Вариант №2.

1.Найдите угол между лучом ОВ и положительной полуосью ОХ, если В(3;3).

2.Решите треугольник ВСD, если В=45⁰, D=60⁰, ВС=см.

3.Найдите косинус угла A треугольника ABC, если A(3;9), B(0;6), C(4;2).

КР №3.

Вариант №1.

1.Периметр правильного треугольника, вписанного в окружность, равен 45см. Найдите сторону правильного восьмиугольника, вписанного в ту же окружность.

2.Найдите площадь круга, если площадь вписанного в ограничивающую его окружность квадрата равна 72см.

3.Найдите длину дуги окружности радиуса 3см, если её градусная мера равна 150⁰.

КР №3.

Вариант №2.

1.Периметр правильного шестиугольника, вписанного в окружность, равен 48см. Найдите сторону квадрата, вписанного в ту же окружность.

2.Найдите длину окружности, если площадь вписанного в нее правильного шестиугольника равна 72см².

3.Найдите площадь кругового сектора, если градусная мера его дуги равна 120⁰, а радиус круга равен 12см.

КР №4

Вариант №1.

1. Начертите равнобедренный треугольник АВС (АВ=ВС). Постройте фигуру, симметричную данному треугольнику относительно точки С. Укажите параллельные прямые и объясните, почему они параллельны.

2. Начертите ромб АВСD, О - точка пересечения его диагоналей. Постройте фигуру, в которую перейдёт ромб ABCD при параллельном переносе на вектор

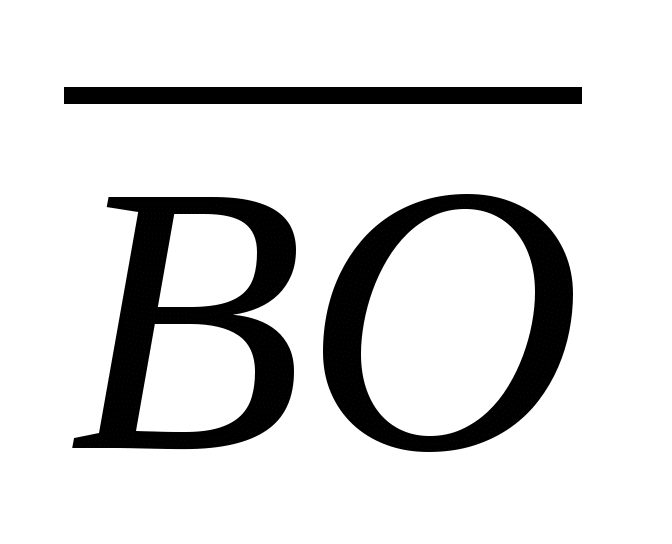
3. Начертите прямоугольный равнобедренный треугольник. Выполните поворот этого треугольника на 90⁰ по часовой стрелке вокруг одной из вершин острого угла.

4. Начертите прямоугольник ABCD и постройте ему симметричный относительно прямой АС.

КР №4

Вариант №2.

1. Начертите равносторонний треугольник АВС. Постройте фигуру, симметричную данному треугольнику относительно точки С. Укажите параллельные прямые и объясните, почему они параллельны.

2. Начертите параллелограмм АВСD, О - точка пересечения его диагоналей. Постройте фигуру, в которую перейдёт параллелограмм ABCD при параллельном переносе на вектор .

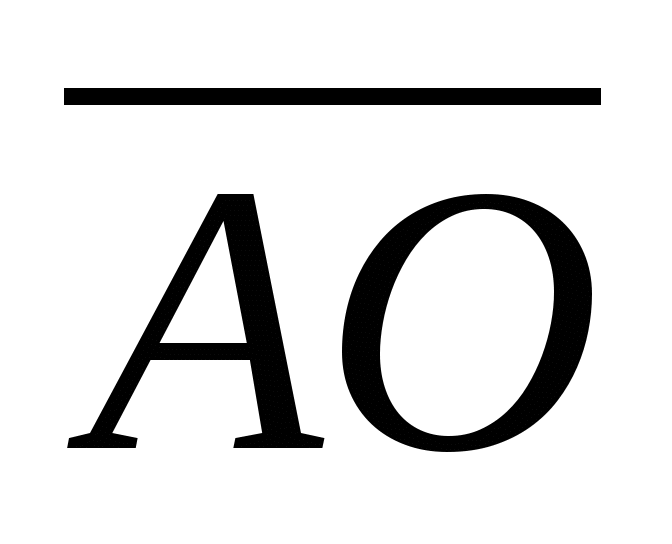3. Начертите прямоугольный равнобедренный треугольник. Выполните поворот этого треугольника на 60⁰ против часовой стрелке вокруг одной из вершин острого угла.

4. Треугольник АВС - правильный. Постройте точку А₁ симметричную точкеА. Относительно прямой ВС. Определите вид четырёхугольника АВА₁С.

Итоговая к/р

Вариант 1

1.В треугольнике АВС точка D - середина стороны АВ ,точка М - точка пересечения медиан.

а) Выразите вектор через векторы и и вектор через векторы и

б) Найдите скалярное произведение

, если АВ=АС=2, <В=75^о.

2. Даны точки А (1;1), В (4;5), С(-3;4).

а) Докажите, что треугольник АВС равнобедренный и прямоугольный.

б) Найдите длину медианы СМ.

3. В треугольнике АВС <А= α >90⁰, <В=β,

высота ВD равна h.

а) Найдите сторону АС и радиус R описанной окружности.

б) Вычислите значение R, если α=120⁰ ,

β=15⁰, h=6 см.

4. Хорда окружности равна а и стягивает дугу в 120⁰. Найдите: а) длину дуги;

б) площадь сектора, ограниченного этой дугой и двумя радиусами.

Итоговая к/р

Вариант 2

1.В параллелограмме АВСD диагонали пересекаются в точку О.

а) Выразите вектор через векторы и и вектор через векторы и

б) Найдите скалярное произведение

, если АВ=2ВС=6, <А=60^о.

2. Даны точки К (0;1), М (-3;-3), N(1;-6).

а) Докажите, что треугольник KMN равнобедренный и прямоугольный.

б) Найдите длину медианы NL.

3. В треугольнике АВС <А= α >90⁰, <В=β,

высота СD равна h.

а) Найдите сторону АВ и радиус R описанной окружности.

б) Вычислите значение R, если α=135⁰ ,

h=3 см., β=30⁰

4. Хорда окружности равна а и стягивает дугу в 60⁰. Найдите: а) длину дуги;

б) площадь сектора, ограниченного этой дугой и двумя радиусами.

Раздел № 6. Мониторинг успешности усвоения учебного материала