- Учителю
- 'Решение задач на проценты', 5 класс
'Решение задач на проценты', 5 класс
Учитель Ученики
-
Самоопределение к учебной деятельности
Цель:
1) включить учащихся в учебную деятельность;
-
определить содержательные рамки урока, продолжить решать задачи на проценты.
Организация учебного процесса на этапе №1:
- Здравствуйте, ребята! Вновь мы встречаемся на уроке математики. А для чего?
- Какую большую тему мы сейчас изучаем?
- Почему мы столько времени уделяем процентам?
- Что вы уже знаете о процентах, чему научились?
- Чему мы еще должны научится?
- Значит, сегодня на уроке будут вами сделаны новые «открытия» для вас в математике. Какого типа наш урок?
- Правильно! Вспомните, какой главный вывод вы уже сделали?
- И, значит, задачи на проценты…
- А поэтому, что нам необходимо повторить?
- Правильно! Итак, начнем!
- Сделать для себя новые открытия;
- Повторять изученное ранее;
- Учиться самостоятельно работать;
- Учиться находить и исправлять свои ошибки;
- Учиться оценивать свою работу.
- Проценты.
- Проценты играют важную роль в жизни человека: экономике, технике, науке.
- Мы знаем определение процента;
- Умеем переводить проценты в дроби и дроби в проценты;
- Решать задачи на проценты.
- Урок открытия новых знаний.
- Проценты - это дроби.
- Задачи на дроби!
- Правила перевода процентов в дроби и дробей в проценты;
-
Актуализация знаний и фиксация затруднений в деятельности
Цель:
1) актуализировать учебное содержание, необходимое и достаточное для восприятия нового материала: понятие процента, правила перевода дробей в проценты и обратно, нахождение части от числа, выраженной дробью;
-
Актуализировать мыслительные операции, необходимые для восприятия нового материала - сравнение, анализ, обобщение;
-
Зафиксировать все повторяемые понятия - в виде алгоритмов, схем, символов;
-
Зафиксировать индивидуальные затруднения в деятельности, демонстрирующее на личностном уровне недостатки в знаниях: все способы решения задач на нахождение процента от числа.
Организация учебного процесса на этапе №1:
-
Вырази в процентах:
1
0,02
2,5
3
4
1*100%=100%
0,02*100%=2%
2,5*100%=250%
![]() * 100% =
* 100% = ![]() = 75%
= 75%
[Ученики работают в тетрадях. Ученик на дополнительной доске выполняет это задание самостоятельно. Затем, открывает решение и весь класс сравнивает свои результаты решением их на доске. В тетради выставляют «+» и «?»]
Вопрос к отвечающему ученику:
- Какое правило использовал при выполнении задания?
- Правила перевода числа в проценты: чтобы перевести число в проценты, надо это число умножить на 100 и поставит знак «%».
[На столе ряд формул]
- Можно ли это правило записать с помощью формулы?
- Найди эту формулу на столе.
- Да.
-[Находит и показывает ребятам. Затем крепит к доске]
а=а*100 %
-
[Фронтальная работа]
-
Верно ли, что 30%=1/3?
- Чем вы воспользовались для доказательства?
- Есть ли формула, выражающая это правило?
- Найди ее на столе.
-
Верно ли, что 78% больше половины?
-
По заданной схеме составь задачу.
[на доске заготовлена схема]
- Какого типа задача?
- Вспомните алгоритм нахождения части от числа.
- Какой формулой выражается этот алгоритм?
- Решите задачу.
Индивидуальное задание:
- Сформулируйте задачу так, чтобы она стала задачей на проценты.
Нет, т.к. 30%=30/100=3/10, 3/10<>1/3
- Правилом перевода процентов в число: чтобы перевести проценты в число, надо количество процентов разделить на 100.
- Да.
[Ученик находит необходимую формулу и показывает ее ребятам, затем крепит к доске]
р%=р/100=0,01р
- Да, т.к. половина - это 50%, а 78%>50%.
- На школьном дворе 40 деревьев, ¾ из них - клены. Сколько кленов на школьном дворе?
- Нахождение части от числа, выраженной дробью.
- Чтобы найти часть от числа, выраженную дробью, надо число умножить на дробь.
[Ученик выбирает формулу, показывает ее классу и крепит к доске]
b=a*m/n
40*3/4=30 (д) [решают на листе, ответ комментируют с места, учитель записывает на доске]
-
Выявление причины затруднения и постанова цели деятельности
Цель:
1) организовать коммуникативное взаимодействие, в ходе которого фиксируется затруднение в учебной деятельности;
2) постановки цели урока и согласование темы урока;
- Что нужно сделать, чтобы задача на дроби стала задачей на проценты?
- Сформулируйте задачу.
- Составьте схему к задаче.
- Сравните схемы двух задач.
- Что находим в первой задаче?
- Что надо найти во второй задаче?
- Чему же будем учиться сегодня на уроке? Какова цель урока?
- Тема урока…
-Правильно. Запишем ее в тетрадь.
- Перевести дроби и числа в условии задачи в проценты.
1 - 100%
¾ - 75%
- На школьном дворе 40 деревьев, ¾ из них - клены. Сколько кленов на школьном дворе?
- Они похожи.
- Часть от числа выраженной дробью.
- Процент от числа.
- Находить проценты от числа.
- «Нахождение процента от числа».
-
Построение проекта выхода из затруднения
Цель:
1) организовывать коммуникативные взаимодействия для построения нового способа действия, устраняющего причину затруднений;
2) зафиксировать новый способ действия в знаковой и вербальной форме.
Организация учебного процесса на этапе №4:
- Решите эту задачу.
- Ребята, я увидела несколько вариантов решения:
а) 40:100*75=30 - верное ли это решение.
- Смысл этого решения
б) 40*![]()
Что означает дробь ![]()
- Какое действие выполняем с этой дробью?
- Повторим действия, которые выполняются при этом решении (в решении №3)
в) 40*![]() - откуда дробь
- откуда дробь ![]() ?
?
- К какому типу задач мы свели решение нашей задачи?
- В чем различие решения этих задач?
- Повторим, какие действия мы выполняли при нахождении процента от числа?
- Мы нашли способ решения задачи?
- Решите эту задачу, используя ваш проект.
[Ученики решают самостоятельно. Учитель проходит и записывает варианты решений.]
- Да, применили правило нахождения процента от числа.
[Формула нахождения процента от числа вывешивается на доску]
- 1) 40:100 - на 1%
2) (40:100)*75 - на 75%
![]() - перевод процентов в дробь
- перевод процентов в дробь
- умножаем на число.
- 1. перевели проценты в дробь,
2. дробь умножили на число.
- Это сократили дробь ![]() , которая означает перевод процентов в дробь.
, которая означает перевод процентов в дробь.
- К нахождению части от числа.
- В задачах на проценты сначала проценты надо перевести в дробь.
1) проценты перевели в дробь,
2) число умножим на дробь.
- Да.
1) 75%=![]() =
=![]()
2) 40*![]() =30 (д).
=30 (д).
Ответ: 30 кленов.
-
Реализации построенного проекта
Цель: переход нового знания в сознание учащихся и сохранить его там в форме алгоритма и формулы процента.
Организация деятельности учащихся на этапе №5:
- Любую ли задачу на нахождение процента от числа можно решить по этому проекту?
- Да.
- Сформируйте алгоритм решения задач этого типа.
- Используя сформированный алгоритм, решите задачу:
Найти 25% от 16.
- Можно ли данные алгоритм представить в виде формулы?
- Что для этого нужно сделать?
- Что поможет сформулировать задачу в общем виде?
- Составьте схему к задаче на нахождение процента от числа в общем виде.
- Чтобы найти процент от числа, необходимо:
1) проценты перевести в дробь (или натуральное число),
2) число умножить на дробь (или натуральное число).
1) 25%=1/4.
2) 16*1/4=16/4=4.
Ответ: 4.
- Да.
- Сформулировать задачу в общем виде.
- Схема и задача.
[Обсуждаем смысл схемы]
- Используя алгоритм, решите задачу в общем виде.
- Что мы получим?
- Что можно найти по этой формуле?
- Как можно назвать эту формулу?
- Что нового вы узнали?
- А для чего?
- Так чем же сейчас займемся?
a - 100% - целое.
b - это p% от числа a, т.е. часть от числа, выраженная в процентах.
Надо найти часть от числа, выраженного в процентах.
-
p% = p/100
-
b = a* p/100
- Формулу b=a*p/100
- Процент от числа.
- Формулой процентов.
- Мы узнали алгоритм нахождения процента от числа и формулу процента.
- Чтобы применять их при решении задач.
- Будем тренироваться применять алгоритм и формулу при решении задач на нахождение процента от числа.
-
Первичное закрепление к внешней речи
Цель: зафиксировать новое учебное содержание (алгоритм нахождения процента от числа и формулу процента) во внешней речи.
Организация учебного процесса на этапе №5:
[решение у доски с проговариванием алгоритма]
№351 (б, л)
б) 30% от 15 мл
-
30%=
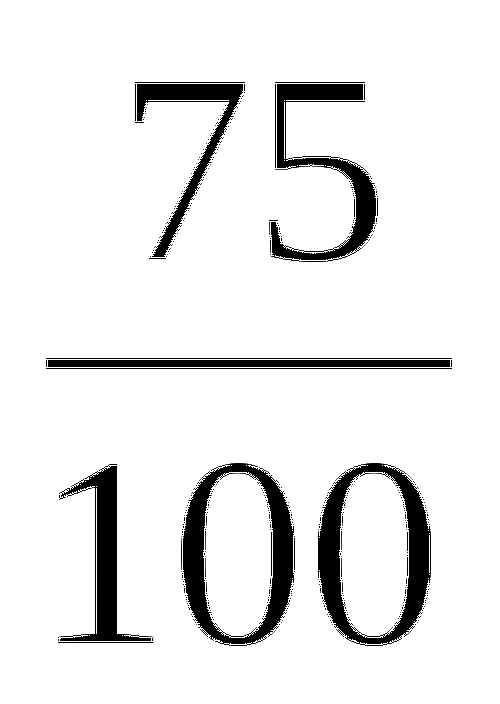 =
=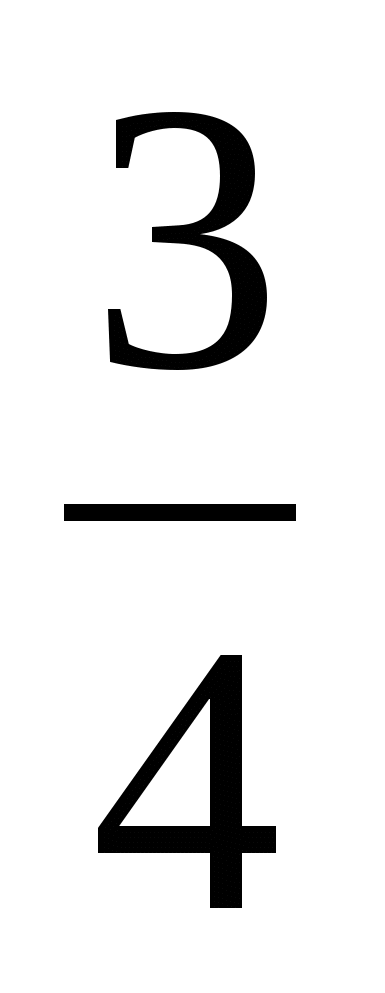 =0,3
=0,3 -
15*0,3=4,5 (мл)
Ответ: 4,5 мл.
л) 35,6% от b.
-
35,6%=35,6:100=0,356
-
b*0,356=0,356b
№356 (2) - у доски ученик.
1 сп. 1) 100%+4%=104% - через год.
2) 104%=104:100=1,04
-
1200*1,04=1248 (р) - через год.
2 сп. 1) 4%=4:100=0,04
2)1200*0,04=48 (р) - прибавки
-
48+1200=1248 (р) - через год.
- Вы научились применять новый алгоритм и формулу процента?
- А как это проверить?
- Верно. Итак, самостоятельная работа.
- Да!
- Написать самостоятельную работу!
-
Самостоятельная работа с самопроверкой по эталону
Цель: проверить умение применять новые учебные знания [алгоритм нахождения % от числа и формулу процента] в типовых условиях на основе сопоставления своего решения с эталоном доля самопроверки.
Организация учебного процесса на этапе №6:
№351 (в, к):
в) 200% от 72 л.
к) 12% от а.
№353 (1) - задача.
[После выполнения работы, ученики сверяют по эталону, обсуждаются и исправляются ошибки]
- Работа окончена. Какой следующий этап нашей работы?
- А как это проверить?
- Верно. Итак, самостоятельная работа.
- Проверяем!
- Самопроверка:
мы должны проверить по образцу ответы т поставить «+» если ответ верен и «?», если ответ не верен.
- Затем проверить по эталону правильность применения правил.
- Выяснить и исправить ошибку.
- Оценить свою работу.
На доске таблица:
№
Количество ошибок:
351 (в)
-
351 (к)
-
353
-
Те ребята, которые без ошибок справились с задание, выполняют дополнительное задание. (№351 з, м)
[проверка по эталону]
-
Включение в систему знаний и повторение
Цель:
-
тренировать навыки использования нового содержания совместно с ранее изученным;
-
повторить учебное содержание которое пригодится на следующих уроках.
Организация учебного процесса на этапе №7:
Решение задач у доски.
Задача №1:
Длина и ширина прямоугольника соответственно 8 см и 6 см. Длину уменьшили на 30%, а ширину увеличили на 15%. Как и на сколько уменьшится площадь прямоугольника.
Решение:
-
30%=0,3 на столько уменьшится длина.
8*0,3=2,4 (см)
8-2,4=5,6 (см) - новая длина.
-
15%=0,15
6*0,15=0,9 (см) - увелич. ширину
6+0,9 (см) - новая ширина.
-
8*6=48 (см2) - площадь первого прямоугольника.
-
5,6*6,9=38,64 (см2) - площадь второго прямоугольника.
-
48-38,64=9,36 (см2) - площадь второго прямоугольника уменьшилась.
Ответ: уменьшилась на 9,36 см2.
Задача №2:
Первые три часа туристы шли со скоростью 4 км/ч. После привала их скорость увеличилась на 20% и они прошли еще 2 км. С какой средней скоростью двигались туристы?
Решение:
-
3*4=12 (км) - прошли за 3 ч.
-
20% = 0,2
4*0,2=0,8 (км/ч) - увеличилась скорость.
4+0,8=4,8 (км/ч) - новая скорость.
-
4,2*2=8,4 (км) - прошли за 2 ч.
-
12+8,4=20,4 (км) - весь путь.
-
3+2=5 (ч) - все время.
-
V ср =
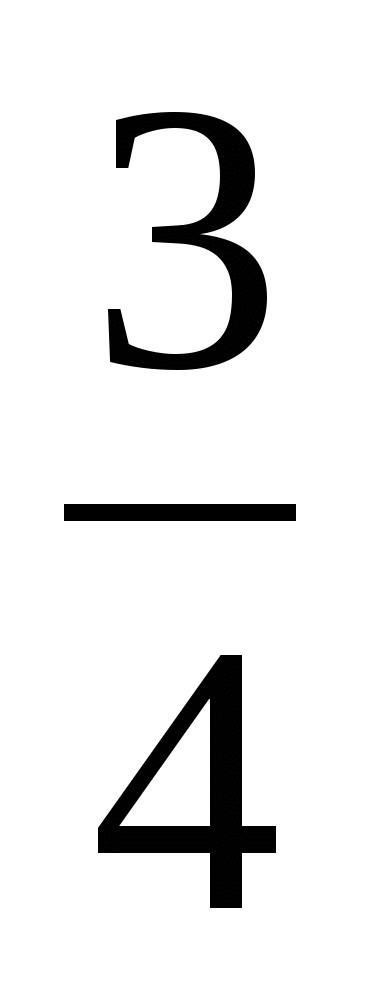
V ср = ![]() = 4,08 (км/ч) - средняя скорость.
= 4,08 (км/ч) - средняя скорость.
Ответ: 4,08 км/ч.
-
Рефлексия
Цель:
-
зафиксировать новое содержание, изученное на уроке (алгоритм нахождения процента от числа и применение формулы процента);
-
оценить собств. деятельность;
-
зафиксировать затруднения;
-
обсудить домашнее задание.
Организация учебного процесса на этапе №8:
- Ребята, какая тема нашего урока?
- Цель урока?
- Что нового вы узнали?
- Какую цель каждый ставил перед собой?
- Достигли ли цели?
- В листах самоконтроля поставьте оценку за этапы.
- Новый прием.
- Применение нового правила.
- С/р.
- Над чем надо поработать еще?
Оцените свою работу за урок!
Спасибо. Запишите домашнее задание.
§ 2 п. 2 (алгоритм)
№405 (2 по выбору)
№406 (1)
№425 * твор. здание на оценку.
Спасибо за урок. Успехов! До скорой встречи!
- Нахождение процента от числа.
- Научиться находить процент от числа.
- Что процент от числа можно находить не только по правилу нахождения процентов, а по алгоритму и формуле процентов.
[Ставят оценки]
- Научиться находит процент от числа.
[ставят оценку в листах самоконтроля]
Поднимают «смайлики»:
«желтый» - 5;
«зеленый» - 4 (усвоил, но есть ошибки);
«синий» - не понял.
-
Тема: «Задачи на проценты. Нахождение процента от числа».
2) Тип урока: открытие новых знаний.
3) Цель:
1. Формировать способность выведения нового способа решения задачи на нахождение процента от числа и применения его к решению задач.
2. Развитие мыслительных операций (сравнение, анализ, синтез).
Оборудование, демонстрационный материал:
1) Задания для актуализации:
№1: 1, ![]() , 0,02, 0,004, 2,5;
, 0,02, 0,004, 2,5;
№2: 1%, 100%, 46%, 0,4%, 0,02%.
П1. a=a*100%
П2. P%=p:100=![]() =0,01p
=0,01p
№5.
b=a*![]()
b=a:100*p
Алгоритм нахождения процента от числа:
-
представить проценты в виде дроби или натурального числа;
-
выполнить умножение.
Формула процента:
b= a*![]() =a*0,01p
=a*0,01p
Раздаточный материал.
Эталон для самопроверки.
№351 (в, к)
в) 200%=2 - представить проценты в виде дроби или натурального числа.
72*2=144 (л) - умножить число на дробь (или натуральное число).
к) 12%=0,12 - представить проценты в виде дроби или натурального числа.
а*0,12=0,12а - выполнить умножение.
№353 (1)
-
10%=0,1 - представить проценты в виде дроби или натурального числа.
2) 20000*0,1 = 2000 (р) - вознаграждение - выполнить умножение.
Ответ: 2000 р.
Эталон к дополнительному заданию:
№351 (з, м)
з) 75% от 80%
75%=0,75
80*0,75= 60%
м) 66![]() % от с
% от с
66![]() % =
% = ![]() =
=![]()
с*![]() =
=![]() с
с
Задача 1.
Длина и ширина прямоугольника 8 см и 6 см соответственно. Длину уменьшили на 30%, а ширину увеличили на 15%. Как и на сколько изменится площадь прямоугольника?
Задача 2.
Первые 3 часа туристы шли со скоростью 4 км/ч. После привала их скорость увеличилась на 20% и она прошли еще 2 км. С какой средней скоростью двигались туристы?