- Учителю
- Урок по алгебре для 10 класса «Комплексные числа и арифметические операции над ними (сложение и вычитание)»
Урок по алгебре для 10 класса «Комплексные числа и арифметические операции над ними (сложение и вычитание)»
Государственное Образовательное учреждение Среднего Профессионального Образования «Колледж сервиса города Оренбурга оренбургской области»
Методическая разработка открытого урока по алгебре и началам анализа по теме:
«Комплексные числа и арифметические операции над ними»
Подготовила
преподаватель математики
первой квалификационной категории
Наговицына Гульлария Шавгатовна
Оренбург, 2014
Тема: Комплексные числа и арифметические операции над ними.
Цель: создать условия для развития мышления старшеклассников через формирование нового понятия - понятия комплексного числа и арифметических действий над ними.
Вид занятия: урок усвоения новых знаний.
Задачи:
образовательные: повторить историю развития чисел; показать необходимость расширения множеств натуральных, рациональных, действительных чисел; расширить множество чисел введением комплексных чисел; ознакомить с арифметическими действиями над комплексными числами;
развивающие: способствовать развитию информационных умений обучающихся, умения работать с текстом слайда; способствовать развитию творческой и мыслительной деятельности обучающихся; продолжить формирование умений четко и ясно излагать свои мысли, анализировать, делать выводы;
воспитательные: активизировать познавательную деятельность учащихся; развитие навыков самостоятельной работы, волевых качеств для достижения результатов, интереса к предмету.
Оборудование: компьютер, проектор, экран, дидактический материал, школьная доска.
План урока:
-
Организационный этап.
-
Актуализация опорных знаний учащихся.
-
Мотивация учебной деятельности учащихся (Постановка цели и задач урока).
-
Первичное усвоение новых знаний и проверка понимания.
-
Первичное закрепление.
-
Рефлексия
-
Подведение итогов занятия.
Подробный конспект урока:
-
Организационный этап.
Приветствие, проверка подготовленности, организация внимания.
Добрый день(утро), ребята. Я рада, что мне представилась возможность провести свой конкурсный урок с вами. Сегодня мы с вами будем работать с числами - простыми и сложными, привычными и необычными. Наш урок я хочу начать со слов, которые говорил Иоганн Гёте: «Числа не управляют миром, но показывают, как управляется мир».
А как вы считаете, верно ли это? (Мнения учащихся - Почему согласны?)
Действительно, числа повсюду - с самого рождения человек окружен числами - дата рождения, рост, вес.
-
Актуализация опорных знаний учащихся.
Чтоб время даром не терять, разминку будем начинать.
Вы уже знакомы со многими числами и умеете с ним работать. Давайте, мы вспомним то, что уже известно вам. И мне понадобится ваша помощь - перед вами расположены числовые множества, которые вы все изучали ранее. Расположите эти круги таким образом, чтобы выстроилась правильная последовательность. ( На столе числовые множества - натуральные, целые, рациональные и действительные числа, один учащийся на доске с помощью магнита выстраивает «круги Эйлера»). А все очень внимательно наблюдают за работой …… Все согласны с полученным результатом?
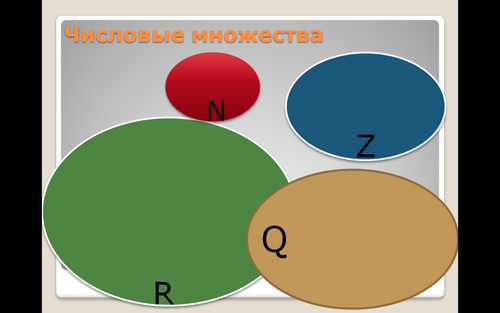
Молодцы. Спасибо.
А что мы знаем о каждом множестве конкретно?
- Первое множество - самое маленькое - это множество натуральных чисел. Как обозначается множество натуральных чисел? (N)
- Приведите примеры натуральных чисел (1.2.3.4.5…….). Хорошо.
- Для чего нужны натуральные числа? ( Для счета предметов)
- Какие операции выполнимы во множестве натуральных чисел? (Сложение, умножение)
- Какие операции не всегда выполнимы во множестве натуральных чисел? (вычитание, деление, извлечение корней)
-Вот вы привели примеры натуральных чисел, я тоже хочу привести вам пример натурального числа. Мой пример - это число -3.(Учащиеся возмущается)
- Вы со мной не согласны? (Не согласны)
- Почему? (Число -3 является целым числом)
- Верно, и это следующее множество. Как обозначается множество целых чисел? (Буквой Z)
- Приведите примеры целых чисел? (-5,-99,-1,0, 5,123 и т.д.) Т.е это натуральные числа, им противоположные и 0.
- Какие операции выполнимы во множестве целых чисел? ( Сложение, вычитание, умножение)
- Какие операции не всегда выполнимы во множестве целых чисел? (деление, извлечение корней)
-Но для решения задачи о деление целого на несколько частей, недостаточно целых чисел и приходится вводить дробные числа.
-Как называется следующее множество? ( Множество рациональных чисел)
- Как обозначается множество рациональных чисел? ( Буквой Q)
- Приведите примеры рациональных чисел? ( 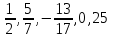 и т.д.)
и т.д.)
- Какие операции выполнимы во множестве рациональных чисел? (Сложение, вычитание, умножение, деление)
- Какие операции не всегда выполнимы во множестве рациональных чисел? (Извлечение корней из неотрицательных чисел)
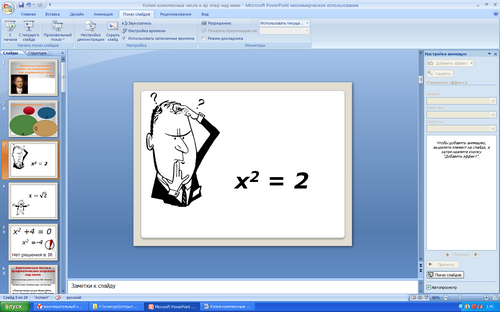
- Однако уравнение x2 = 2 не имеет рациональных корней. Еще в глубокой древности
появилась необходимость введения иррациональных чисел.
-Какое множество образуют рациональные и иррациональные числа? (Множество действительных чисел)
- Как обозначается множество действительных чисел? (Буквой R)
- Приведите примеры действительных чисел? (Все известные нам до этого числа + число пи.)
- Какие операции выполнимы во множестве действительных чисел? (Сложение, вычитание, умножение, деление).
- Какие операции не всегда выполнимы во множестве действительных чисел? (Извлечение корней из произвольных чисел)
- Замечательно!
В этом множестве мы можем извлекать корни из некоторых чисел. 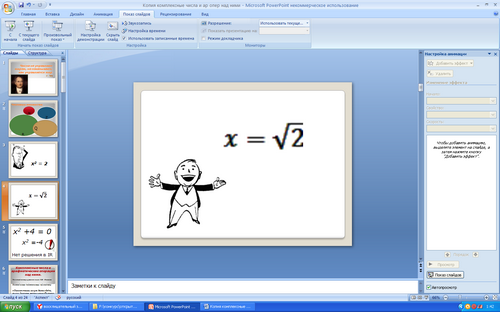
Попробуем решить уравнение: x2 +4 = 0.(Решения нет)
Все записи сегодня на уроке вы будете вести в маршрутных листах, которые лежат у вас на столе. Подпишите их и приступим к работе.

-
Мотивация учебной деятельности учащихся.
- Но мы ж с вами до этого не сдавались и сейчас не сдадимся! И подумаем, а может быть существуют другие числа, с помощью которых мы сможем записать корни этого уравнения?
-Да, такие числа существуют! Про них мы сегодня и поговорим.
У вас на столах маршрутные листы на урок, в которых мы будем сегодня вести все записи.
Тема урока: Комплексные числа и арифметические операции над ними.
Чтобы не было разногласий в постановке ударения, обратимся к толковому словарю русского языка, где написано, что , когда речь идет о числах, предпочтительнее ударение ставить на второй слог, это специальный математический термин. У математиков даже есть шутка по этому поводу - кОмплексными могут быть обеды, числа бывают только комплексными. Но если вы поставите ударение на первый слог, ошибки в этом тоже нет.
(На доску прикрепить круг, изображающий множество комплексных чисел, которое больше всех остальных).
Исходя из темы, как вы думаете, на какие вопросы нам нужно ответить на уроке? (Какие числа называются комплексными и как с этими числами работать.)
-Верно.
-Как вы уже все знаете, именно в это время в нашей стране проводятся зимние олимпийские игры «Сочи 2014».Посмотрите видеофрагмент ( ВИДЕО) Открытие олимпиады - это шоу, которое потрясло воображение всего мира! Сколько музыки и света, энергии и положительных эмоций!

-Чтобы музыка играла, а лампы горели, нам необходим электрический ток. Комплексные числа используются в научных расчетах схем переменного тока.
Живой портрет.
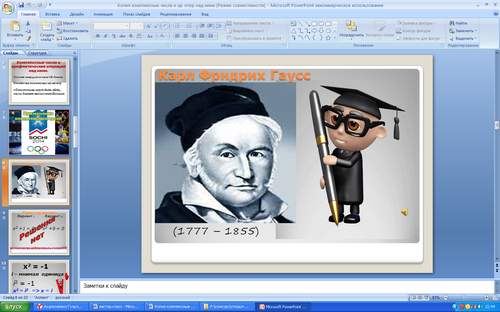
- Но не только в физике можно найти применение комплексным числам! Без комплексных чисел ракеты не полетели бы в космос, субмарины не погружались бы на морские глубины, биологи не посчитали бы изменения в популяции животных. Сам термин «комплексные числа» ввёл немецкий математик Карл Фридрих Гаусс. Мы сегодня с вами наряду с учеными окунемся в мир комплексных чисел.
-
Первичное усвоение новых знаний и проверка понимания.
Начнем с известного. Предлагаю вам решить простейшие уравнения по вариантам:
Вариант 1
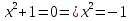 - решения нет в R
- решения нет в R
Вариант 2
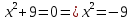 - решения нет в R
- решения нет в R
- Какие у вас получились ответы? (У всех решение нет).
- На самом деле эти уравнения имеют решение во множестве комплексных чисел. Чтобы найти их, рассмотрим определение в ваших маршрутных листах:
-
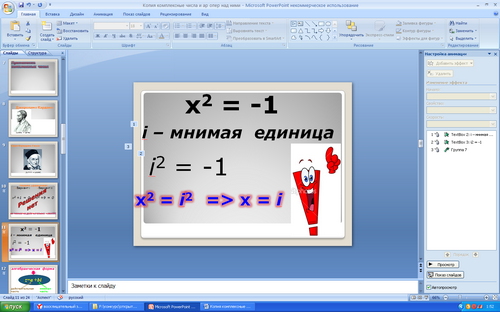
Корень уравнения x2 = -1 называется мнимой единицей и обозначается буквой i.
Таким образом, символ i удовлетворяет условию i2 = -1.
- Так что же теперь получается, мы можем извлекать квадратный корень из отрицательных чисел? (Да, с помощью нового символа)
И теперь, решая уже известное нам уравнение 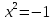 , мы получаем, что
, мы получаем, что 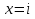 .
.
- А что же такое само комплексное число? Для этого обратимся к понятию комплексного числа:
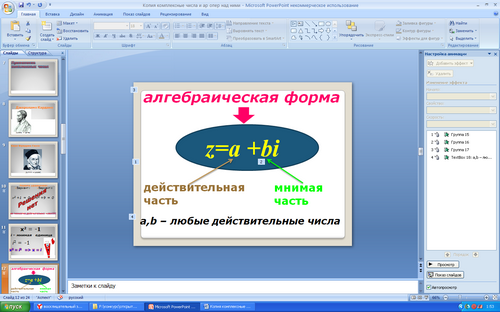
Комплексным числом называется сумму вида z=a +bi, где a - действительная часть,
bi - мнимая часть.
Множество комплексных чисел принято обозначать буквой С.
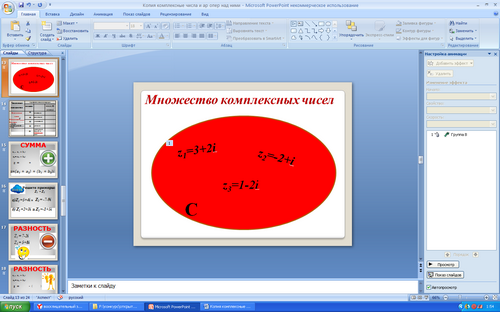
Примеры:
z1=3+2i, z2=-2+i, z3=1-2i и т.д.
Приведите свои примеры.
Примеры учащихся.
Мы определили с вами, какие числа называются комплексными числами. Посмотрите, это множество больше, чем все остальные. Как вы думаете, можно ли с этими числами работать так же, как и с другими? (Да)
Сегодня на уроке мы познакомимся с операциями сложения и вычитания комплексных чисел. Другие арифметические действия над комплексными числами вы сможете рассмотреть позже самостоятельно с помощью методических рекомендаций, которые останутся у вас.
-
Действия над комплексными числами в алгебраической форме.
-Хоть эти числа пока необычны для нас, они мало чем отличаются от других привычных нам чисел. Поэтому действия с комплексными числами не представляют особой сложности. Как же складываются комплексные числа? Для ответа на данный вопрос мы воспользуемся определением
: 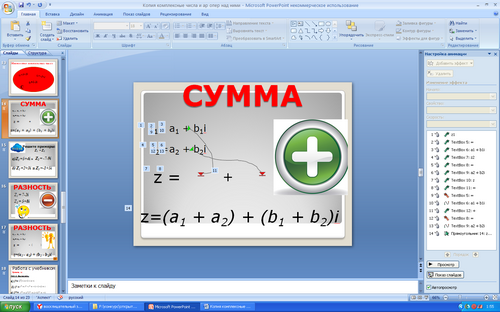
Суммой двух комплексных чисел z1 = a1 + b1i и z2 = a2 + b2i называется комплексное число вида z=z1 + z2 = (a1 + a2) + (b1 + b2)i.
-Назовите действительные части этих комплексных чисел. (a1 и a2).
-Верно. Назовите мнимые части этих комплексных чисел. (b1i и b2i )
- Получается, чтобы сложить 2 комплексных числа, нужно к действительной части первого к.ч. прибавить действительную часть второго к.ч., к мнимой части первого к.ч прибавить мнимую часть второго комплексного числа.
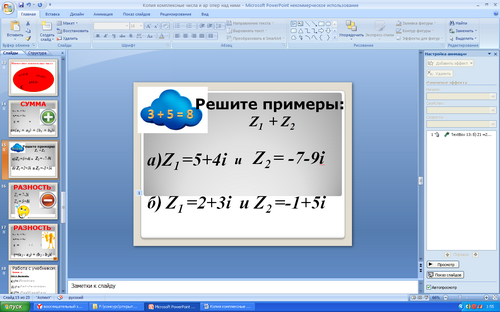
Например, 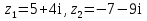
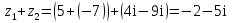 .
.
Второй пример попробуйте решить вы и к доске прошу …….
- Молодцы!
- Какая операция является обратной для сложения? (Вычитание)
Повернитесь к своим одноклассникам, образуя группы по 4 человека, и вместе выполните задание:
Вам предложены два комплексных числа.
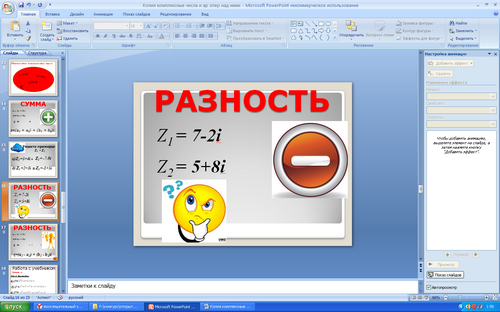
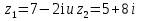 .
.
Назовите действительные и мнимые части этих комплексных чисел. Выполните операцию вычитание. Попробуйте вывести правило вычитания комплексных чисел. На это вам отводится 1 минута. Кто справится раньше, поднимаем руки.
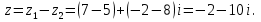
Разностью двух комплексных чисел z1 = a1 + b1i и z2 = a2 + b2i называется комплексное число вида z=z1 - z2 = (a1 - a2) + (b1 - b2)i.
- Как вы уже заметили, формулы, определяющие правила действий над комплексными числами в алгебраической форме, не нуждаются в запоминании. И получаются автоматически, если формально выполнить соответствующие действия над двучленами a1 + b1i и a2 + b2i
-
Первичное закрепление.
- В курсе алгебры основной школы комплексные числа хорошо рассмотрены в учебнике Мордковича для профильных классов. Чтобы не быть голословными, рассмотрим несколько примеров из учебника:
Работа с учебником:
Уровень А:
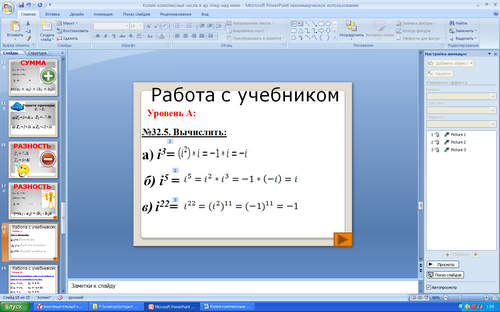
- Первое задание - разминка. Исходя из условия i2 = -1 вычислим:
№32.5. Вычислить:
а) i3 ; б) i5 ; в) i22 .
На местах решаются задания, один учащийся на каждый пример у доски, самопроверку проводим с помощью презентации или доски.
-Как можно расписать степень?
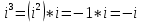
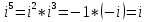
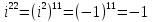
- Молодцы! Вы с легкостью справляетесь со всеми задачами! Применим наши новые знания о сумме и разности комплексных чисел для выполнения следующего здания:
Уровень В:
№32.10 Для комплексных чисел z1 и z2 найдите их сумму z1 + z2 и разность z1 - z2 , если:
а) z1 = 1+i, z2 = 1-i;
б) z1 = 1+i, z2 = -1+2i;
в) z1 = -i, z2 = 1-i;
г) z1 = i3 +4 i4 , z2 = i2 -3(-i)3
-
Рефлексия.
-Замечательно! Молодцы! С помощью новых знаний, вы справились с заданиями. Теперь мы можем сказать, что выполнили задачи, поставленные на уроке?
(Да, мы узнали, какие числа называются комплексными и научились их складывать и вычитать)
Закончите предложения:
-
Сегодня я узнал(а)…
-
У меня вызвало затруднение…
-
Урок дал мне для жизни…
-
Подведение итогов занятия.
Какой важный вывод, вы можете сделать из нашего урока?
(Какие бы проблемы и трудности нас не окружали в жизни, это не значит, что мы в безысходности. Это значит, что нам не хватает знаний, умений.)
-Верно, ведь недаром Иоганн Гете говорил, что числа не управляют миром, но показывают как управляется мир. И чтобы вы в любой ситуации могли управлять своей жизнью, вы должны стремиться к получению новых знаний.
Спасибо за урок! До свидания!
Маршрутный лист
Фамилия _____________________________ Имя _____________________
Тема урока: Комплексные числа и арифметические операции над ними.
Решить уравнение: 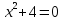
Решить уравнение:
Вариант 1
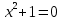
Вариант 2
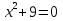
Корень уравнения x2 = -1 называется мнимой единицей и обозначается буквой i
-
i2 = -1
Комплексным числом называется сумму вида z=a +bi, где a- ,
bi -
Приведите свои примеры
Суммой двух комплексных чисел z1 = a1 + b1i и z2 = a2 + b2i называется комплексное число вида z=z1 + z2 = (a1 + a2) + (b1 + b2)i.
Решить примеры:
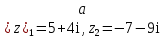
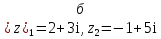
Работа по группам (по 4 человека)
Найдите разность двух комплексных чисел:
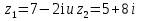
Разностью двух комплексных чисел z1 = a1 + b1i и z2 = a2 + b2i называется ___________________________________________________________________________
Работа с учебником:
№32.5. Вычислить:
а) i3 =
б) i5 =
б) z1 = 1+i, z2 = -1+2i;
№32.10 Для комплексных чисел z1 и z2 найдите их сумму z1 + z2 и разность z1 - z2 , если
Закончите предложения:
-
Сегодня я узнал(а)…
-
У меня вызвало затруднение…
-
Урок дал мне для жизни…