Делимость суммы и разности чисел

</<font face="Times New Roman, serif">Тема урока: Делимость суммы и разности чисел (6 класс)

Цели:

• Закрепить признаки делимости суммы и разности при выполнении упражнений;

• Развивать навыки решения задач и примеров;

• Сформировать внимательное и аккуратное выполнение делимости суммы и разности чисел.

Организационный момент. Доброе утро ребята. Мы продолжаем с вами изучение делимости суммы и разности чисел. Чтобы нам перейти к закреплению изученного материала, давайте вспомним материал предыдущего урока.Подготовительный этап

Метод: репродуктивный

Форма: фронтальный опрос

Учитель

Ученик

Доска(опора)

Проверим домашнее задание.

Возникли какие-нибудь сложности при выполнении домашней работы?

Вспомним правила:

- сформулируйте определение кратного

- сформулируйте определение делителя

- Найдите НОК(15,20)

- Найдите

НОД(14,20)

- сформулируйте правило делимости произведения

- сформулируйте правило делимости сложения и разности чисел

Найдите НОК(15,20)

- Найдите

НОД(14,20)

Этап применения действия.

Открываем тетради. Записываем «Классная работа. Делимость суммы и разности чисел »

Записываем номер 784 (один их учащихся решает на доске)

Решите задачу 778 на доске и в тетрадях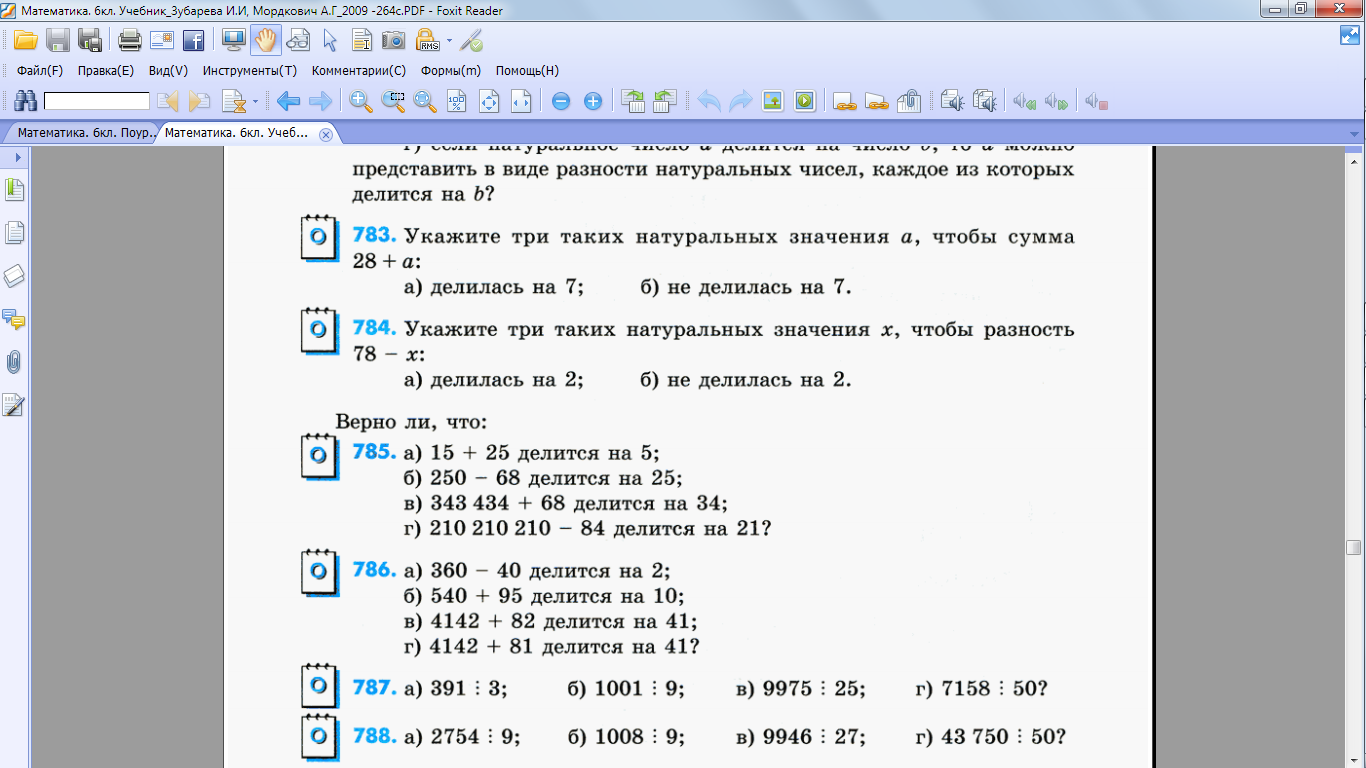

МОЛОДЦЫ!

5. решить номер 797

МОЛОДЦЫ!!!

Открывают тетради. Записывают «Классная работа» и тему урока.

Рефлексия:

С каким действием мы сегодня работали?

Что вы можете сказать о делимости произведения, делимости суммы и разности чисел?

Возникли ли у вас сложности при делении одночлена на одночлен?

Запишем домашнее задание: повторить определения, правила, номера: №801(б,в), 802

-Делимостью

- если хотя бы один из множителей делится на некоторое число, то и произведение

делится на это число

- нет.