- Учителю
- Конспект урока алгебры в 8 классепо теме «Решение задач с помощью квадратных уравнений»
Конспект урока алгебры в 8 классепо теме «Решение задач с помощью квадратных уравнений»
Конспект урока алгебры в 8 классе
Тема: Решение задач с помощью квадратных уравнений.
Цели урока: А) Общеобразовательные: формирование учебного действия - «Исследование процессов реальной действительности с помощью аппарата квадратных уравнений». Раскрытие перед учащимися этапов процесса решения задач прикладного характера: а) мотивация; б) анализ условия задачи; в) моделирование;г)решение задачи внутри математической модели; д) содержательная интерпретация полученных результатов.
Б) Воспитательные: формирование учебных умений по развитию устной математической речи учащихся.
Методы обучения: частично поисковый, проблемный.
Ход урока.
Проверка домашнего задания.
2 этап. Формирование учебного действия по исследованию процессов реальной действительности и современного производства.
Задача 1. В одной из лесосек близ Новосибирска в т985 году было 200000 м3 древесины. Количество древесины последовательно возрастает каждый год на одно и то же число процентов, в результате чего в 1987 году оно составило 212180 м3 . Найти ежегодный прирост древесины в процентах.
Методика работы с задачей.
1 этап. Мотивационный. Учитель должен учащимся сказать, что такие задачи приходится решать специалистам различных отраслей производства.
2 этап. Анализ условия задачи. Учащимся задаются вопросы:
-
Какое количество древесины было в лесосеке в 1985 году?
-
Какой прирост древесины в процентах был в 1986 и 1987 годах?
-
Назовите процент прироста древесины за каждый год.
-
Какое количество древесины стало в лесосеке в 1987 году?
3 этап. Моделирование. На данном этапе условие задачи, сформулированное на естественном языке переводится на язык математики. От реальной ситуации переходят к построению адекватной математической модели.
Х - ежегодный процент прироста древесины.
200000̇̇ .(1+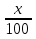 ) _ количество древесины в лесосеке к концу 1986 года.
) _ количество древесины в лесосеке к концу 1986 года.
200000. (1+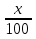 ) .(1+
) .(1+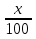 ) _ количество древесины в лесосеке к концу 1987 года.
) _ количество древесины в лесосеке к концу 1987 года.
Согласно условию задачи мы имеем уравнение:
200000̇̇ .(1+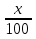 )2 = 212180 (1)
)2 = 212180 (1)
Уравнение (1) _ математическая модель реальной ситуации.
Математическая задача: решить уравнение (1).
4 этап. Решение задачи внутри математической модели.
200000̇̇ .(1+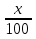 )2 = 212180 ;
)2 = 212180 ;
10000 .(1+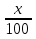 )2 = 10609;
)2 = 10609;
10000 + 200х +х2 _ 10609 = 0;
Х2 + 200х _ 609 = 0 (2)
Решаем квадратное уравнение (2).
Ответ для математической задачи: х1 =3; х2 = _ 203.
5 этап. Критическое осмысление полученных результатов. Поскольку за х принят процент прироста древесины, то х2 = _ 203 не удовлетворяет условию задачи. Следовательно, х = 3%.
Ответ: ежегодный прирост древесины составляет 3%.
Задача 2. Бригада медеплавильщиков с целью ускорения плавки дважды усовершенствовала технологию производства за счёт: 1) увеличения концентрации дутья кислорода и 2) повышения температуры дутья. Поэтому дважды равномерно была повышена производительность труда. Найти рост производительности труда каждый раз, если бригада за смену увеличила плавку с 5 до 6,05 т.
Методика работы с задачей.
1 этап. Мотивационный.
2 этап. Анализ условия задачи.
3 этап. Моделирование.
Х _ десятичная дробь, показывающая рост производительности труда в процентах после первого усовершенствования технологии производства.
5000 . (1 + х) _ объем производства после первого вида усовершенствования;
5000 . (1 + х) . (1 + х) _ объем производства после второго вида усовершенствования.
Согласно условию задачи имеем уравнение:
5000 . (1 + х) . (1 + х) =6050
Или 100 (1 + х)2 = 121 (1). Уравнение (1) _ математическая модель задачи.
4 этап. Решение задачи внутри математической модели:
100 х2 + 200 х _ 21 = 0;
Х1 = 0,1; х2 = _ 2,1.
Ответ для математической задачи: х1 = 0,1; х2 = _ 2,1.
5 этап. Критическое осмысление полученных результатов.
Для практической задачи подходит только х = 0,1.
Вывод: рост производительности труда составляет 10%.
Домашнее задание:
Задача 1. При постройке сооружения требовалось вырыть 8000 м3 грунта в определенный срок. Работа была закончена на 8 дней раньше срока, так как бригада землекопов ежедневно перевыполняла план на 50 м3. Найти в какой срок бригада должна была закончить работу. Найти ежедневный процент перевыполнения.
Ответ: за 40 дней; 25%.
Задача 2. Для лесозащитных насаждений отведена полоса длиной 24 км и шириной 50 м. по нормам лесопосадки (измеряемым в человеко-днях) 18 человек должны закончить работу к намеченному сроку. Но, увеличив дневную норму на 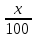 га за человеко-день, 15 рабочих закончили посадку на два дня раньше намеченного срока. Какую площадь предполагалось засаживать за один день одному рабочему и сколько засаживали в действительности?
га за человеко-день, 15 рабочих закончили посадку на два дня раньше намеченного срока. Какую площадь предполагалось засаживать за один день одному рабочему и сколько засаживали в действительности?
Ответ: 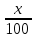 га и 1га.
га и 1га.
Выводы по уроку.