План-конспект урока по геометрии 'Равнобедренный треугольник и его свойства' (7 класс)

ПЛАН-КОНСПЕКТ УРОКА

Равнобедренный треугольник и его свойства

ФИО (полностью)

Керзенмей Чойгана Кара-ооловна

Место работы

МБОУ СОШ с.Эйлиг-Хемский

Должность

учитель

Предмет

математика

Класс

7

Тема урока

Равнобедренный треугольник и его свойства.

Базовый учебник

Л.С.Атанасян, В.Ф.Бутузов и другие «Геометрия 7-9 класс»

8. Цели урока: сформировать представления учащихся о равнобедренном треугольнике и его свойствах.

9. Задачи:

- обучающие:

• знакомство учащихся с понятиями равнобедренного и равностороннего треугольника и их свойствами;

• формирование умения учащихся применять рассмотренные свойства при решении задач.

-развивающие:

• развитие устной и письменной речи;

• развитие логического мышления (определять и объяснять понятия, читать рисунок, анализировать, сравнивать, выделять главное, доказывать);

• развитие навыков исследовательской деятельности.

-воспитательные:

• воспитание навыков самоконтроля и взаимоконтроля, правильной самооценки, умения работать в паре;

• воспитание самостоятельности учащихся через организацию индивидуальной деятельности;

• воспитывать культуру речи, внимание к точности формулировок

10. Тип урока: урок введения нового материала с использованием ЭОР.

11. Формы работы учащихся: фронтальная, парная, индивидуальная.

Ход урока.

1. Актуализация опорных знаний учащихся.

1). Фронтальный опрос уч-ся с использованием презентации:

- Что называется треугольником?

- Назовите основные элементы треугольника.

- Как найти периметр треугольника?

- Что называется медианой треугольника?

- Что называется высотой треугольника?

- Что называется биссектрисой треугольника?

- Какие треугольники называются равными?

- Что называется теоремой?

1. Какие теоремы нам уже известны? (Свойство смежных углов и свойство вертикальных углов.)

2. Любая теорема состоит из условия и заключения. Как вы понимаете, что может означать словосочетание «условие теоремы», а что - «заключение теоремы»? (Условие - это уже известные факты, о которых говорится в теореме, а заключение - это то, что нужно получить, доказать.)

- Сформулируйте первый признак равенства треугольников.

2). Работа у доски (по готовым чертежам - 2уч-ся).

Задача 1.

Найти на рисунке треугольники, равные по первому признаку.

B

D

C

A

E

G

F

Задача 2.

Прямые АС и ВД пересекаются в точке О так, что ВО = СО, АО = ДО. Найти угол В и отрезок СД, если угол С равен 60⁰, а отрезок АВ = 12 см.

2. Объяснение нового материала.

1. Определение равнобедренного треугольника; его боковые стороны и основание.

2. Определение равностороннего треугольника.

3. Доказательство двух теорем о свойствах равнобедренного треугольника.

Чертеж, краткую запись условия и заключение теоремы, а также основные этапы доказательства полезно записать на доске и в тетрадях учащихся.

1. Теорема. В равнобедренном треугольнике углы при основании равны.

Дано: ∆АВС - равнобедренный треугольник,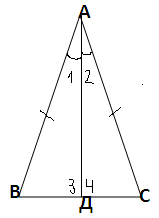

ВС - основание. рис.1

Доказать: ∟В=∟С.

Доказательство:

Проведем биссектрису АД треугольника (рис.1).

∆АВД=∆АСД по двум сторонам и углу между

ними (АВ=АС по условию, АД - общая сторона, ∟1=∟2,

так как АД - биссектриса). Значит, ∟В=∟С, что и требовалось доказать.

Это свойство в дальнейшем часто используется при решении задач и доказательств теорем, поэтому оно должно быть хорошо усвоено.

2. Теорема. В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.

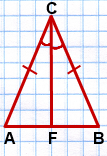
Дано: Дано:

∆ ABC,

AC=BC,

CF - биссектриса.

Доказать: CF - медиана и высота.

Доказательство:

Рассм. треугольники ACF и BCF (важно правильно их !)

1) AC=BC (по условию (как боковые стороны равнобедренного треугольника))

2) ∠ACF=∠BCF (так как CF - по условию).

3) сторона CF - общая.

Значит, ∆ ACF=∆ BCF (по двум сторонам и углу между ними).

Из равенства треугольников следует равенство соответствующих сторон и углов.

Таким образом, AF=BF, следовательно, CF - .

∠AFC=∠BFC. А так как эти углы - смежные, значит, они прямые:∠AFC=∠BFC=90º.

Значит, CF - .

Что и требовалось доказать.

Мы установили, что биссектриса, медиана и высота равнобедренного треугольника, проведенные к основанию, совпадают. Поэтому справедливы также утверждения:

1. Высота равнобедренного треугольника, проведенная к основанию, является медианой и биссектрисой.

2. Медиана равнобедренного треугольника, проведенная к основанию, является высотой и биссектрисой.

3. Закрепление изученного материала.

1. Решить задачу №108.

Дано: ∆ АВС- равнобедренный треугольник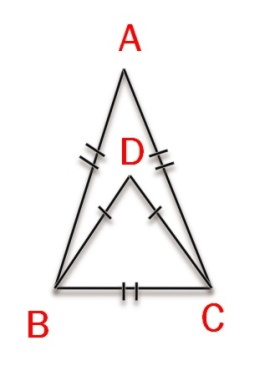

АВ=АС

Р∆ АВС= 40 см

∆ ВСD- равносторонний треугольник

Р∆ ВСD= 45 см.

Найти: АВ, ВС.

Решение:

ВС=СД=ВД (по условию), Р∆ ВСD= 45 см=3ВС, отсюда ВС=45:3=15(см).

По условию Р∆ АВС= 40 см, ВС=15см, тогда АВ+АС=40-15=25(см). Так, по условию ∆ АВС -равнобедренный, то АВ=АС=25:2=12,5(см).

Ответ: АВ=12,5см; ВС=15см.

IV. Физминутка.

V. Лабораторная работа.(учащимся раздаются листы с заданиями лабораторной работы)

Цель: 1)Выяснить какие треугольники называются равнобедренными (равносторонними);

2)Какими свойствами они обладают.

Оборудование: масштабная линейка, транспортир.

Задание 1. Измерьте стороны треугольника, запишите результат измерений:

1. АВ = ………см; BC = ………см; AC = ………см;

2. MN = ………см; NK = ………см; MK = ………см;

3. ST = ………см; TR = ………см; SR = ………см;

4. DE = ………см; EF = ………см; DF = ………см;

5. OQ = ………см; QG = ………см; OG = ………см.

Задание 2. Треугольники ∆ABC, ∆MNK, ∆STR - равнобедренные. Сравните результаты измерений и дайте определение равнобедренного треугольника:

Треугольник называется равнобедренным, если_____________________________

______________________________________________________________________

Треугольник ∆OQG - равносторонний. Посмотрите на результаты измерений, дайте определение равностороннего треугольника:

Треугольник называется равносторонним, если ____________________________

Можно, ли равносторонний треугольник назвать равнобедренным? ____________

А равнобедренный - равносторонним? ____________________________________

VI. Итог урока. Рефлексия.

1. Какая тема нашего урока?

2. Какова цель нашего урока?

3. Выполнен ли план урока?

4. Какие новые понятия мы сегодня узнали?

5. Какой треугольник называется равнобедренным?

6. Какие стороны называются боковыми, основанием?

7. Какой треугольник называется равносторонним?

8. Является ли равносторонний треугольник равнобедренным?

9. Каким свойством обладают углы в равнобедренном треугольнике?

10. Каким свойством обладают углы в равностороннем треугольнике?

VII. Домашнее задание. Изучить п.18 с доказательством теорем, ответить на вопросы 10-12 на стр.48, решить задачи №104, 107 и 117.