- Учителю
- Урок «Геометрическая прогрессия» для 9 класса
Урок «Геометрическая прогрессия» для 9 класса
Пасичник Надежда Николаевна - учитель математики МОУ СОШ № 6
с углубленным изучением английского языка г. Апатиты
Геометрическая прогрессия в задачах
(9 класс)
Тип урока: семинар-практикум
Цели и задачи:
Образовательные:
-
Закрепить и расширить знания учащихся по основному блоку темы «Геометрическая прогрессия».
-
Научить применять полученные знания для моделирования и дифференциального решения задач разных уровней усвоения учебного материала и различного содержания.
-
В результате учебного исследования подвести к изучению последнего блока темы «Сумма бесконечной геометрической прогрессии».
Конструктивные:
-
Создать условия для индивидуального развития учащихся: стимулировать учебный успех одноклассников; сотрудничать внутри группы и с учителем.
-
Предоставить возможность применения учащимися математических знаний к изучению действительности и решению практических задач; развитию их логического мышления и познавательного интереса
Развивающие:
-
Интеллектуальное развитие учащихся, формирование качеств мышления, характерных для математической деятельности.
-
Формирование представлений об идеях и методах математики, о математике как форме
описания и методе познания действительности.
-
Формирование представлений о математике как части общечеловеческой культуры.
Форма работы на уроке: групповая. [Урок составлен в соответствии с разноуровневой технологией обучения - как способ реализации внутренней уровневой дифференциации ]
Рабочее название группы
Сокр.
Классификация
в ИТО
Уровень обучения
Назначение группы для достижения учебных целей
Натуралисты
Н![]()
Группа выравнивания
М
-
достижение обязательного уровня обучения;
-
умение применять формулы в процессе решения задач
Историки
И![]()
Группы поддержки
О
-
закрепление на достигнутом уровне;
-
расширение знаний в процессе работы с новой информацией
Экономисты
Э![]()
О
Исследователи
И![]()
Группа развития
П
-
выход на более высокий уровень знаний в процессе работы, требующей доказательства или исследования
Условные обозначения уровней: М - минимальный; О - общий; П - продвинутый
Оборудование: ПК, мультимедиа проектор
Приложения:
-
Тест по теме «Геометрическая прогрессия» - карточки для каждого учащегося
уровней О и П
-
Карточка - О Б Р А З Е Ц - для каждого учащегося уровня М
-
ИНДИВИДУАЛЬНЫЕ карточки - для каждого учащегося уровня М
-
КАРТОЧКИ для ГРУППОВОЙ работы
-
Презентация «Геометрическая прогрессия» - сопровождение в Power Point
С Х Е М А У Р О К А
Этап урока
Время
(мин.)
Учебный материал
Содержание работы
Самоопределение к деятельности (организация)
1
Слайды 1-3
ПР. 5
Объявление темы; настрой на достижение поставленных целей
Контроль
9
ПРИЛОЖЕНИЯ 1, 2, 3
И![]() Э
Э![]() И
И![]() - однородный состав класса
- однородный состав класса
Работа с тестом «Геометрическая прогрессия»
Н![]()
Работа с индивидуальными карточками по представленному ОБРАЗЦУ
Актуализация знаний
3
И![]() Э
Э![]() И
И![]() - однородный состав класса
- однородный состав класса
Взаимопроверка выполненного теста
Н![]()
Сдача тетрадей учителю.
Опрос по формулам
Постановка учебной задачи
1
ПР.ИЛОЖЕНИЕ 4
Н![]() И
И![]() Э
Э![]() И
И![]() - работа в группах
- работа в группах
Группы получают задания соответственно тематике группы
Выполнение учебной задачи
10
Н![]() И
И![]() Э
Э![]() И
И![]() - работа в группах
- работа в группах
Обсуждение и решение задач на листах. Консультация учителя. Подготовка к «защите» полученного задания
«Публичная» защита
15 - по 5
Слайды 4- 13 ПР. 5
Н![]() И
И![]() Э
Э![]()
Представители групп выступают с прорешанными задачами: представляют классу содержание задач, предлагают порешать на уроке или дома.
Заключительный этап
6
И![]() - группа создает эвристическую ситуацию, нацеливающую учащихся на изучение следующей темы. Учитель объявляет тему следующего занятия и уточняет Д/З:
- группа создает эвристическую ситуацию, нацеливающую учащихся на изучение следующей темы. Учитель объявляет тему следующего занятия и уточняет Д/З:
-
[ Задачи для Д / З ] , представленные группами.
-
Заполнить «магический квадрат» так, чтобы в каждом столбце и в каждой строке получилась геометрическая прогрессия
-
27
36
6
8
С О Д Е Р Ж А Н И Е У Ч Е Б Н О Г О М А Т Е Р И А Л А
ПРИЛОЖЕНИЕ 1---------------------------------------------------------------------------------------------------------
Тест по теме «Геометрическая прогрессия»
I вариант
1. В геометрической прогрессии ![]() ;
; ![]() . Найдите знаменатель q.
. Найдите знаменатель q.
1) 9; 2) 3; 3) ![]() ; 4)
; 4) ![]()
2. В геометрической прогрессии ![]() ;
; ![]() . Найдите шестой член этой прогрессии.
. Найдите шестой член этой прогрессии.
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]()
3. В геометрической прогрессии ![]() ;
; ![]() . Найдите сумму пяти первых членов этой
. Найдите сумму пяти первых членов этой
прогрессии.
1)18,8; 2) 80,2; 3) 48,4; 4) 39,6
4. Найдите первый член геометрической прогрессии, если ![]() и
и ![]() .
.
1) 4; 2) 6; 3) 2; 4) 8,5
5.В возрастающей геометрической прогрессии ![]() , сумма первых трех ее членов равна 26.
, сумма первых трех ее членов равна 26.
Найдите ![]() .
.
1) 32; 2) 162; 3) 54; 4) 48
II вариант
1. В геометрической прогрессии ![]() ;
; ![]() . Найдите знаменатель q.
. Найдите знаменатель q.
1) 2; 2) ![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]()
2. В геометрической прогрессии ![]() ;
; ![]() . Найдите пятый член этой прогрессии.
. Найдите пятый член этой прогрессии.
1) ![]() ; 2) 40,5; 3) -13,5; 4)
; 2) 40,5; 3) -13,5; 4) ![]()
3. В геометрической прогрессии ![]() ;
; ![]() . Найдите сумму шести первых членов этой
. Найдите сумму шести первых членов этой
прогрессии.
1) -9,3; 2) 6,3; 3) 3,2; 4) -18,9
4. Найдите первый член геометрической прогрессии, если ![]() и
и ![]() .
.
1) 3; 2) 2; 3) 4; 4) 1,5
5. В убывающей геометрической прогрессии ![]() , сумма первых трех ее членов равна 42.
, сумма первых трех ее членов равна 42.
Найдите ![]()
1) 6; 2) 3; 3) -81; 4) 1,5
Ответы к тесту
№ задания
1
2
3
4
5
I
4
2
3
1
3
II
3
3
4
1
2
ПРИЛОЖЕНИЕ 2----------------------------------------------------------------------------------------------------------
Карточка - О Б Р А З Е Ц
№ 1
(![]() ) - геометрическая прогрессия 1,6; 0,8;…
) - геометрическая прогрессия 1,6; 0,8;…
Найдите следующие три члена прогрессии.
Решение
1,6; 0,8;…- геометрическая прогрессия; ![]() ;
; ![]() ;
; ![]()
![]() ;
; ![]() ;
; ![]()
Ответ: 0,4 ; 0,2 ; 0,1
№ 2
(![]() ) - геометрическая прогрессия,
) - геометрическая прогрессия, ![]() ;
; ![]() ;
; ![]()
Решение
![]() ;
; ![]() 0,05 Ответ:
0,05 Ответ: ![]() 0,05
0,05
№ 3
(![]() ) - геометрическая прогрессия,
) - геометрическая прогрессия, ![]() ;
; ![]() ;
; ![]()
Решение
![]()
![]()
![]() ;
; ![]() Ответ:
Ответ: ![]()
№ 4
(![]() ) - геометрическая прогрессия,
) - геометрическая прогрессия, ![]() ;
; ![]() ;
; ![]()
Решение
![]()
![]()
![]() ;
; ![]() ;
; ![]() Ответ:
Ответ: ![]()
№ 5
(![]() ) - геометрическая прогрессия,
) - геометрическая прогрессия, ![]() ;
; ![]() ;
; ![]()
Решение
![]() ;
;
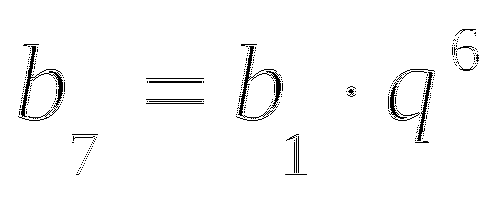
Ответ: ![]()
ПРИЛОЖЕНИЕ 3-------------------------------------------------------------------------------------------------------
ИНДИВИДУАЛЬНЫЕ карточки
Карточка 1
(![]() ) - геометрическая прогрессия № 2
) - геометрическая прогрессия № 2 ![]() ;
; ![]() ;
; ![]()
№ 3 ![]() ;
; ![]() ;
; ![]()
№ 4 ![]() ;
; ![]() ;
; ![]()
№ 5 ![]() ;
; ![]() ;
; ![]()
Карточка 2
(![]() ) - геометрическая прогрессия
) - геометрическая прогрессия
№ 1 0,7 ; 2,1 ; …
Найдите следующие три члена прогрессии.
№ 3 ![]() ;
; ![]() ;
; ![]()
№ 4 ![]() ;
; ![]() ;
; ![]()
№ 5 ![]() ;
; ![]() ;
; ![]()
Карточка 3
(![]() ) - геометрическая прогрессия № 2
) - геометрическая прогрессия № 2 ![]() ;
; ![]() ;
; ![]()
№ 3 ![]() ;
; ![]() ;
; ![]()
№ 4 ![]() ;
; ![]() ;
; ![]()
№ 5 ![]() ;
; ![]() ;
; ![]()
Карточка 4
(![]() ) - геометрическая прогрессия
) - геометрическая прогрессия
№ 1 0,9 ; 1,8 ; …
Найдите следующие три члена прогрессии.
№ 2 ![]() ;
; ![]() ;
; ![]()
№ 4 ![]() ;
; ![]() ;
; ![]()
№ 5 ![]() ;
; ![]() ;
; ![]()
Карточка 5
(![]() ) - геометрическая прогрессия № 2
) - геометрическая прогрессия № 2 ![]() ;
; ![]() ;
; ![]()
№ 3 ![]() ;
; ![]() ;
; ![]()
№ 4 ![]() ;
; ![]() ;
; ![]()
№ 5 ![]() ;
; ![]() ;
; ![]()
Карточка 6
(![]() ) - геометрическая прогрессия
) - геометрическая прогрессия
№ 1 0,3 ; 1,8 ; …
Найдите следующие три члена прогрессии.
№ 2 ![]() ;
; ![]() ;
; ![]()
№ 3 ![]() ;
; ![]() ;
; ![]()
№ 4 ![]() ;
; ![]() ;
; ![]()
Ответы к карточкам
№ карточки
№ з а д а н и я
№ 1
№ 2
№ 3
№ 4
№ 5
1
---
![]()
![]()
![]()
![]()
2
6,3; 18,9;
56,7
---
![]()
![]()
![]()
3
---
![]()
![]()
![]()
![]()
4
3,6; 7,2;
14,4
![]()
---
![]()
![]()
5
---
![]()
![]()
![]()
![]()
6
10,8;64,8;
388,8
![]()
![]()
![]()
---
ПРИЛОЖЕНИЕ 4-----------------------------------------------------------------------------------------------------------
КАРТОЧКИ для ГРУППОВОЙ работы ( Решения к заданиям)
НАТУРАЛИСТЫ
№ 1 Расцвели весной в саду цветочки. На первой клумбе - 1 цветок, на второй - 2 цветка, на третьей - 4цветка и т.д. Сколько цветочков расцвело на всех 6 клумбах этого сада ?
№ 2 Птичка в понедельник подлетела к окну и склевала 5 зернышек, а в каждый последующий день - в 3 раза больше. Какой сегодня день, если птичка уже склевала (на вчерашний день ) 147620 зернышек ?
№ 3 Некий вид бактерий размножается делением со скоростью 1дел./сек. (каждую секунду бактерии раздваиваются). Лаборант заметил, что если посадить в пустой сосуд I бактерию, то через одну минуту сосуд окажется полным. Через какое время наполнится сосуд, если вначале в него посадить 2 бактерии ? [ Задача для Д / З ]
Решение
№ 1 ![]() 63(цветка)
63(цветка)
№ 2 ![]() 10; Сегодня - четверг,
10; Сегодня - четверг, ![]() понедельник.
понедельник.
№ 3 Задача на смекалку 59 секунд
ИСТОРИКИ
№ 1 Легенда о награде изобретателя шахматной игры. По преданию, индийский царь Шерам, восхищенный остроумием шахматной игры, призвал к себе изобретателя шахмат Сету и сказал ему: «Я желаю достойно вознаградить тебя ! Исполню любое твое желание...» Сета попросил положить на первую клетку доски 1 пшеничное зерно, на вторую - 2 зерна, на третью - 4 зерна и т. д. Сколько нужно зерен ? Среднеазиатский математик Бернулли получил верный ответ:
18 446 744 073 709 551 615 зерен.
Задания:
-
а) Округлите ответ так, чтобы первая цифра была значущей, а остальные - нули.
-
б) За сколько лет можно собрать по всей Земле урожай для причитающейся награды,
если масса одного зернышка приближенно равна четверти грамма, а годовой урожай Земли равен![]() тонн?
тонн?
№ 2 Русский фольклор. Шли семь старцев. У каждого старца по семи костылей. На каждом костыле по семи сучков. На каждом сучке по семи кошелей. В каждом кошеле по семи пирогов. В каждом пироге по семи воробьев. Сколько всего воробьев ? [ Задача для Д / З ]
Решение
№ 1 а) ![]() ; б)
; б) ![]() (зерен) - за 1 год;
(зерен) - за 1 год; ![]() 100(лет)
100(лет)
№ 2 ![]() 117649 (воробьев)
117649 (воробьев)
ЭКОНОМИСТЫ
В Сберегательном банке России для срочных вкладов начисляют сложные проценты или
"проценты на проценты"
Формула сложного процентного роста для расчета ![]() - суммы через n лет, если S - начальная сумма, а банк начисляет p% годовых.
- суммы через n лет, если S - начальная сумма, а банк начисляет p% годовых.
![]()
Пользуясь формулой сложного процентного роста, решите задачи:
№ 1 Какая сумма будет на срочном вкладе через 4 года, если банк начисляет 10% годовых , а
начальный вклад равен 2 000 рублей?
№ 2 Какой капитал надо отдать в рост под 20% годовых, чтобы через 3 года получить
вместе с процентами не менее 10 000 рублей? (Результат округлите до целых)
[ Задача для Д / З ]
Решение
№ 1 ![]() ;
; ![]() 2928,2 (рублей)
2928,2 (рублей)
№ 2 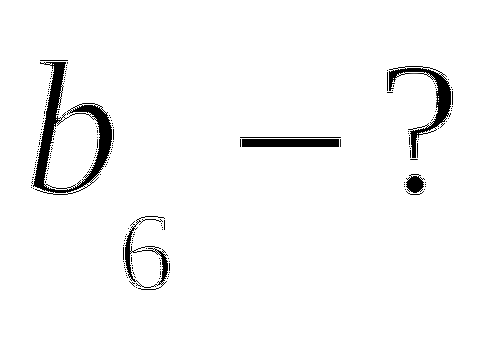 5788 (рублей)
5788 (рублей)
ИССЛЕДОВАТЕЛИ
Парадокс Зенона
-
Древнегреческий философ Зенон Элейский еще в V веке до нашей эры обратил внимание на противоречивость движения. Зенон рассуждал так: « Если лягушка прыгает вперед на половину заданного пути, затем на половину половины пути и т.д., то она никогда не дойдет до конечного пункта, - путь ее бесконечен…»
ЗАДАНИЯ:
№1 Изучите «Парадокс Зенона». Объясните, в чем же суть парадокса?
№ 2 Рассмотрите пример геометрической прогрессии при ![]() ( например,
( например, ![]() ) . Вычислите сумму членов
) . Вычислите сумму членов![]() при
при ![]() - это бесконечно убывающая геометрическая прогрессия.
- это бесконечно убывающая геометрическая прогрессия.
№3 Можете вывести формулу в общем виде ? Тогда запишите эту формулу !
№4 И все же: какой путь проскачет лягушка ? [ Задача для Д / З ]
Решение
№ 2 ![]()
![]()
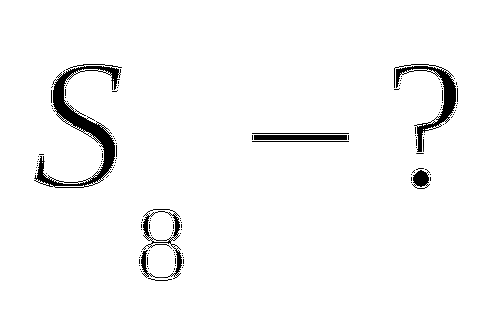 =
= ![]() - сумма n первых членов геометрической
- сумма n первых членов геометрической
прогрессии , где ![]() ,
,![]() . При этих условиях прогрессия становится
. При этих условиях прогрессия становится
бесконечно убывающей, и ![]() .
.
№ 3
![]() , при
, при ![]() и
и ![]()
![]() - общая формула
- общая формула
№ 4 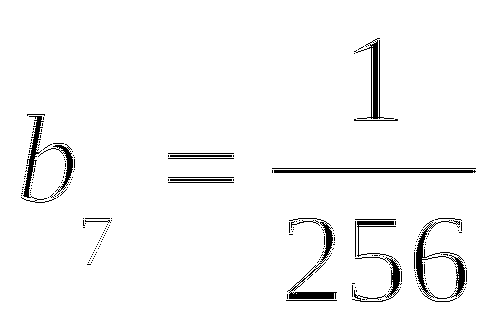 1 - путь лягушки
1 - путь лягушки
ПРИЛОЖЕНИЕ 5 -----------------------------------------------------------------------------------------------------------
Презентация «Геометрическая прогрессия» - сопровождение в Power Point
-------------------------------------------------------------------------------------------------------------------------------------
МАГИЧЕСКИЙ квадрат (Решение)
-
27
54
108
216
9
18
36
72
3
6
12
24
1
2
4
8