- Учителю
- Урок по геометрии для 7 класса по теме «Теорема о сумме углов треугольника»
Урок по геометрии для 7 класса по теме «Теорема о сумме углов треугольника»
МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА № 11
МУНИЦИПАЛЬНОГО ОБРАЗОВАНИЯ ГОРОД - КУРОРТ АНАПА
Номинация «Физико-математические науки (математика)»
План - конспект урока по теме:
«Теорема о сумме углов треугольника»
7 класс
Разработала: Быкова Е.А., учитель математики высшей квалификационной категории
Анапа, 2013
Открытый урок по геометрии в 7-м классе на тему:
«ТЕОРЕМА О СУММЕ УГЛОВ ТРЕУГОЛЬНИКА»
Тип урока: изучение нового материала.
Цели:
-
Образовательные: повторить и обобщить знания о треугольнике; доказать теорему о сумме углов треугольника и классифицировать треугольники по углам и сторонам; научиться применять полученные знания при решении задач.
-
Развивающие: развивать геометрическое мышление, интерес к предмету, познавательную и творческую деятельность учащихся, математическую речь, умение самостоятельно добывать знания.
-
Воспитательные: развивать личностные качества учащихся, таких как целеустремленность, настойчивость, аккуратность, умение работать в коллективе; содействовать формированию активной жизненной позиции учащихся.
Вид урока: комбинированный.
Оборудование: мультимедийный проектор, компьютер.
Презентация в программе Microsoft Office Power Point 2007 (Приложение 1)
Литература: учебник «Геометрия 7-9» авторов Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кодомцев. Издательство «Просвещение». Москва, 2008.
Ход урока
I. Анализ результатов контрольной работы.
1. Проанализировать характерные ошибки, допущенные в контрольной работе.
2. Выполнить работу над ошибками.
II. Изучение нового материала.
1. Решить задачу по готовому чертежу на доске (см. рис.).
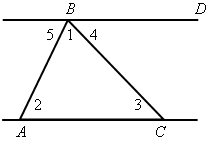
На рисунке ВD || АС.
Найдите сумму углов треугольника АВС.
2. Вслед за решением этой задачи перед учащимися ставится вопрос: случайно ли сумма углов данного треугольника АВС оказалась равной 180° или этим свойством обладает любой треугольник?
Поиск ответа естественно приводит к формированию теоремы о сумме углов треугольника.
3. Доказательство теоремы о сумме углов треугольника.
4. Внешний угол треугольника.
Определение: Внешним углом треугольника называется угол, смежный с каким-нибудь углом этого треугольника.
Сколько внешних углов можно построить у любого треугольника?
Теорема: Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним. Рассмотреть доказательство по учебнику п.30.
5. Классификация треугольников. Перед введением классификации треугольников по углам (п. 31) учащимся задается вопрос: «Может ли треугольник иметь: а) два прямых угла; б) два тупых угла; в) один прямой и один тупой угол?».
Ответы должны быть обоснованы с помощью теоремы о сумме углов треугольника.
Теорема о сумме углов треугольника позволяет классифицировать треугольники не только по сторонам, но и по углам.
Записать в тетрадях вывод из этих ответов (следствие из теоремы о сумме углов треугольника): в любом треугольнике либо все три угла острые, либо два угла острые, а третий - тупой или прямой.
6. Ввести понятия остроугольного, тупоугольного и прямоугольного треугольников и обратить внимание учащихся на названия сторон прямоугольника, треугольника - гипотенуза и катет (рис. 126 учебника, модели треугольников).
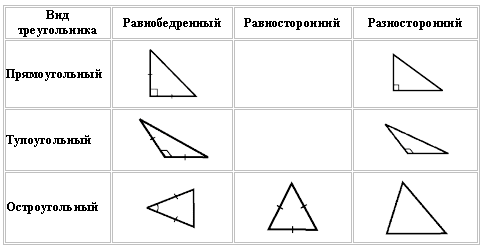
7. Устно решить задачи.
В треугольнике АВС угол А равен 90°, при этом другие два угла:
а) один острый, а другой может быть прямым;
б) оба острые;
в) один острый, а другой может быть тупым .
2. В треугольнике АВС угол В - тупой, при этом другие два угла могут быть:
а) только острыми;
б) острый и прямой;
в) острый и тупой.
3. В остроугольном треугольнике могут быть:
а) все углы острые;
б) один тупой угол;
в) один прямой угол.
4. Найдите угол С треугольника АВС, если угол А= 65º, угол В= 57º.
5. Найдите угол С равностороннего треугольника АВС, если В = 70°
III. Закрепление изученного материала.
1. Решить задачи на доске и в тетрадях.
IV. Итоги урока.
Домашнее задание: изучить пункты 30-31; ответить на вопросы 1; 3; 4; 5 на с. 89; решить задачи №№ 223 (а), 225. Составить кроссворд по теме "Треугольник".