Тема урока: Сложение и вычитание дробей с разными знаменателями

Цели урока:

• познавательная: изучить алгоритм нахождения суммы, разности дробей с разными знаменателями;

• развивающая: учить планировать, анализировать;

• воспитательная: воспитание внимательности, поддержание интереса к предмету, взаимосотрудничество.

Формы работы: фронтальная, индивидуальная, коллективная.

Оборудование:

• таблица "Сложение и вычитание долей, обыкновенных дробей с разными знаменателями";

• презентация;

• дидактическая игра "Математическое лото";

• индивидуальные карточки.

Методы: словесно-репродуктивный метод, проблемное изложение.

Этапы урока

Цели

Виды деятельности

1.Организационный

Поддержание интереса к предмету

Историческая справка

2.Актуализация знаний

Повторить ранее изученный материал

Устные упражнения

Индивидуальные задания

3.Изучение новой темы

Составить алгоритм сложения дробей

Учить планировать, анализировать

Объяснение учителя

Коллективная работа

4.Тренировочные упражнения

Формирование умений и навыков

Индивидуальная работа «Мат. лото»

5.Итог урока

Проверить уровень усвоения темы

Алгоритм

Домашние задание

Ход урока

Организационный момент

Ребята, сегодня на уроке мы продолжим изучение обыкновенных дробей.

Вы знаете, что дроби возникли в древности, так как были необходимы в практической жизни. Разные народы по-разному обозначали дроби, по своим правилам выполняли действия.

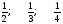Например, древние египтяне (в XX веке до н.э.) использовали лишь единичные дроби,

и т.д., то есть дроби, числительные которых равны 1. Все вычисления с дробными числами производились с помощью этих единичных дробей, что было очень сложно. Поэтому вычисления с дробями могли выполнять лишь специально обученные писцы.

Лишь в XVI веке стали рассматривать дроби с любым натуральным показателем, и были приняты общие правила действия над ними. Но ещё долго считалось, что действия с обыкновенными дробями - сложнейшее дело.

Недаром у немцев сохранилась поговорка: «Попасть в дробь», что означает попасть в тупик, в трудное положение.

Вы, школьники XXI века н.э., шагнули далеко вперёд. Вы немало знаете о дробях, немало умеете. Некоторые скажут, что сократить дробь, привести дроби к общему знаменателю, сравнить дроби не так уж и сложно. Верно.

Чтобы свободно оперировать с дробями, надо хорошо знать правила, алгоритмы и точно им следовать. И тогда никто «не попадёт в дробь».

Актуализация знаний

Для успешной работы на уроке нужны знания и умения

1. по сокращению дробей;

2. по приведению дробей к общему знаменателю;

3. умение складывать и вычитать дроби с одинаковыми знаменателями.

Подумайте, какие понятия нужно вспомнить.

К доске для решения задач вызвать 4 ученика.

№ 1. Приведите дроби к общему знаменателю:

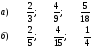
№ 2. Приведите дроби к общему знаменателю:

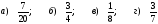
№ 3.1.Замените обыкновенную дробь десятичной:

3.2. Замените десятичную дробь обыкновенной:

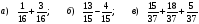№ 4. Выполните действия:

Фронтальная работа с классом (вопросы задают либо учащиеся, либо учитель).

1.Что, значит, сократить дробь?

2.Что является общим знаменателем дробей?

3.Какое число называется дополнительным множителем? Как он находится?

4.Алгоритм приведения дробей к общему знаменателю. Что называется общим кратным?

5.Правило сложения (вычитания) дробей с одинаковыми знаменателями.

Проверим, как ребята справились с заданиями.

Первый ученик читает задание. Объясняет, как выполнил.

Комментарий учителя: Вспомнили «Как найти общий знаменатель дробей, если один из знаменателей делится на другие; если знаменатели взаимно простые».

Второй ученик читает задание. Объясняет, как выполнил.

Комментарий учителя: Вспомнили все способы нахождения наименьшего общего кратного чисел.

Третий ученик читает задание. Объясняет, как выполнил.

Четвертый ученик читает задание. Объясняет, как выполнил.

Комментарий учителя и дополнения по необходимости.

Проверка домашнего задания

Вопросы учащихся. Образцы решения показать при необходимости.

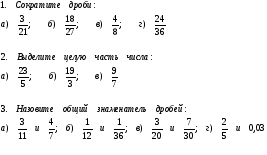Устные упражнения (презентация)

Учитель: «Рада, что в целом класс не «попал в дробь».

Физкультминутка

Изучение нового материала

Римский оратор и писатель Цицерон говорил, что без знаний дробей никто не может признаваться знающим математику.

Вы умеете сравнивать дроби, складывать и вычитать дроби с одинаковыми знаменателями. Но не знаете пока правил сложения, вычитания дробей с разными знаменателями. Значит, есть над чем работать.

Тема урока «Сложение и вычитание дробей с разными знаменателями»

Древние египтяне использовали лишь единичные дроби, другие дроби они представляли через единичные. Составлялись специальные таблицы. Так в древнем папирусе Ринда была такая таблица:

Запишите равенство

Это равенство является решением старинной задачи: « Разделите 7 булок на 12 человек поровну, не разрезая ни одной булки на 12 равных частей».

Ответ: каждый получит часть булки и 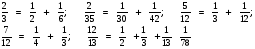часть булки.

Проверим, так ли это.

Найдите сумму дробей

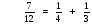Когда встречается трудность, надо попытаться использовать то, что вы знаете, умеете.

Учитель: «Что знаете? Что умеете?» (презентация)

Коллективная работа.

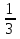
Проанализируем и составим программу (алгоритм) сложения (вычитания) дробей с разными знаменателями (презентация)

1.Найти общий знаменатель дробей (наименьший общий знаменатель дробей)

2.Найти дополнительный множитель к каждой дроби

3.Найти новые числители каждой дроби

4.Сложить (вычесть) полученные дроби с одинаковыми знаменателями

5.Сократить полученную дробь, выделить целую часть (если возможно)

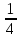Ученики сначала слушают, затем пишут.

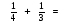Задание выполняет ученик. Комментарий ученика или учителя.

Можно складывать 3 и больше дробей.

Задача. Для нормального питания детям в возрасте от 11 до 15 лет нужно потреблять в сутки белков 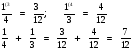кг, жиров 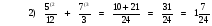кг и углеводов 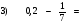кг. Сколько всего этих указанных продуктов необходимо потреблять детям в сутки?

Решение задачи.

Задание выполняет ученик. Комментарий ученика или учителя

Самостоятельная работа «Математическое лото»

(инструкция)

Каждый ученик получает индивидуальный набор карточек с 4 заданиями и лист ответов.

Оценивается работа (на обороте карточек рисунок)

Дополнительное задание:

Задача 1. Масса птицы грифа достигает 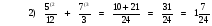ц, а масса африканского страуса 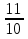ц. Сравните массы птиц. Насколько одна птица тяжелее другой?

Задача 2. Один ученик может убраться в классе за 20 минут, а другой - за 30 минут. Какую часть класса уберут ученики за 1 минуту, если будут работать вместе? За какое время они уберут весь класс вместе?

Итог урока

Учитель: «Ребята, сегодня вы познакомились с алгоритмом сложения и вычитания дробей с разными знаменателями. Какие умения нужны при сложении и вычитании дробей?»

Домашнее задание: п.11, ответы на вопросы, №322 (а, б), 360(г, д, ж, з, к, л).

Оценки за урок.