Рабочая программа по геометрии 8 класс

Пояснительная записка.

Данная рабочая программа ориентирована на учащихся 8 класса, составлена и реализуется на основе следующих документов:

Примерная программа основного общего образования по математике, 2-е издание/ М.: Просвещение, 2010

Авторская программа для общеобразовательных учреждений по геометрии по учебному комплексу авторов Л.С.Атанасян, В.Ф.Бутузов и др, составитель Т.А.Бурмистрова,М.: Просвещение 2011

Федеральный закон «Об образовании в Российской Федерации» от 21 декабря 2012 № 273-ФЗ

Устав МБОУ Грузиновская СОШ

Основная образовательная программа МБОУ Грузиновская СОШ (по реализации БУП-2004) 2014-2015 учебный год (5-11 класс)

Основные цели курса:

-овладение системой математических знаний и умений, необходимых в практической деятельности, продолжения образования;

-приобретение опыта планирования и осуществления алгоритмической деятельности;

-освоение навыков и умений проведения доказательств, обоснования выбора решений;

-приобретение умений ясного и точного изложения мыслей;

-развить пространственные представления и умения, помочь освоить основные факты и методы планиметрии;

-научить пользоваться геометрическим языком для описания предметов.

Задачи обучения:

- научить учащихся выполнять действия над векторами как направленными отрезками;

-познакомить с использованием векторов и метода координат при решении геометрических задач;

- развить умение учащихся применять тригонометрический аппарат при решении геометрических задач;

- расширить знания учащихся о многоугольниках;

- рассмотреть понятия длины окружности и площади круга для их вычисления;

- познакомить учащихся с понятием движения и его свойствами;

- дать начальное представление о телах и поверхностях в пространстве..

Контрольные работы направлены на проверку уровня базовой подготовки учащихся, а также на дифференцированную проверку владения формально-оперативным математическим аппаратом, способность к интеграции знаний по основным темам курса.

Общая характеристика учебного предмета

Геометрия - один из важнейших компонентов математического образования. Она необходима для приобретения конкретных знаний о пространстве и практически значимых умений, формирования языка описания объектов окружающего мира, развития пространственного воображения и интуиции, математической культуры, эстетического воспитания учащихся. Изучение геометрии вносит вклад в развитие логического мышления, в формирование понятия доказательства.

В курсе геометрии 8-го класса продолжается решение задач на признаки равенства треугольников, но в совокупности с применением новых теоретических факторов. Теореме о сумме углов выпуклого многоугольника позволяет расширить класс задач. Формируется практические навыки вычисления площадей многоугольников в ходе решения задач. Особое внимание уделяется применению подобия треугольников к доказательствам теорем и решению задач. Даются первые знания о синусе, косинусе и тангенсе острого угла прямоугольного треугольника. Даются учащимся систематизированные сведения об окружности и её свойствах, вписанной и описанной окружностях. Серьезное внимание уделяется формированию умений рассуждать, делать простые доказательства, давать обоснования выполняемых действий. Параллельно закладываются основы для изучения систематических курсов стереометрии, физики, химии и других смежных предметов.

Курс характеризуется рациональным сочетанием логической строгости и геометрической наглядности. Увеличивается теоретическая значимость изучаемого материала, расширяются внутренние логические связи курса, повышается роль дедукции, степень абстрактности изучаемого материала. Учащиеся овладевают приемами аналитико-синтетической деятельности при доказательстве теорем и решении задач. Систематическое изложение курса позволяет начать работу по формированию представлений учащихся о строении математической теории, обеспечивает развитие логического мышления школьников. Изложение материала характеризуется постоянным обращением к наглядности, использованием рисунков и чертежей на всех этапах обучения и развитием геометрической интуиции на этой основе. Целенаправленное обращение к примерам из практики развивает умения учащихся вычленять геометрические факты, формы, и отношения.

Место предмета в учебном плане ОУ.

Базисный учебный (образовательный) план на изучение геометрии в основной школе отводит 2 учебных часа в неделю в течение каждого года обучения, всего 210 уроков.

Согласно федеральному базисному учебному плану для образовательных учреждений Российской Федерации и учебному плану школу на изучение геометрии в 7 классе отводится 70 часов из расчета: 2 часа в неделю. В соответствии с Постановлением минтруда России о переносе выходных дней в в 2015 году от 27.08. 2014 года №860 в 2014-2015 учебном году в связи с праздничными днями 1.05 программа скорректирована и будет выдана в полном объеме 69 часов за счет уменьшения часов на повторение в конце учебного года.

Последовательность изучения тем:

Тема

Количество часов

Контрольные работы

Повторение

2

Четырехугольники

14

1

Площадь

16

1

Подобные треугольники

19

2

Окружность

15

1

Повторение

6

1

Итого

70

6

Содержание обучения

Повторение курса геометрии 7 класса

Характеристика основных содержательных линий

Четырехугольники

Многоугольник, выпуклый многоугольник, четырехугольник. Параллелограмм, его свойства и признаки. Трапеция. Прямоугольник, ромб, квадрат, их свойства. Осевая и центральная симметрии. Цель: изучить наиболее важные виды четырехугольников - параллелограмм, прямоугольник, ромб, квадрат, трапецию; дать представление о фигурах, обладающих осевой или центральной симметрией. Доказательства большинства теорем данной темы и решения многих задач проводятся с помощью признаков равенства треугольников, поэтому полезно их повторить, в начале изучения темы. Осевая и центральная симметрии вводятся не как преобразование плоскости, а как свойства геометрических фигур, в частности четырехугольников.

Площадь

Цель: расширить и углубить полученные в 5-6 классах представления обучающихся об измерении и вычислении площадей; вывести формулы площадей прямоугольника, параллелограмма, треугольника, трапеции; доказать одну из главных теорем геометрии - теорему Пифагора. Вывод формул для вычисления площадей прямоугольника, параллелограмма, треугольника, трапеции основывается на двух основных свойствах площадей, которые принимаются исходя из наглядных представлений, а также на формуле площади квадрата, обоснование которой не является обязательным для обучающихся. Нетрадиционной для школьного курса является теорема об отношении площадей треугольников, имеющих по равному углу. Она позволяет в дальнейшем дать простое доказательство признаков подобия треугольников. В этом состоит одно из преимуществ, обусловленных ранним введением понятия площади. Доказательство теоремы Пифагора основывается на свойствах площадей и формулах для площадей квадрата и прямоугольника. Доказывается также теорема, обратная теореме Пифагора.

Подобные треугольники

Подобные треугольники. Признаки подобия треугольников. Применение подобия к доказательству теорем и решению задач. Синус, косинус и тангенс острого угла прямоугольного треугольника.

Цель: ввести понятие подобных треугольников; рассмотреть признаки подобия треугольников и их применения; сделать первый шаг в освоении учащимися тригонометрического аппарата геометрии.5 Определение подобных треугольников дается не на основе преобразования подобия, а через равенство углов и пропорциональность сходственных сторон. Признаки подобия треугольников доказываются с помощью теоремы об отношении площадей треугольников, имеющих по равному углу. На основе признаков подобия доказывается теорема о средней линии треугольника, утверждение о точке пересечения медиан треугольника, а также два утверждения о пропорциональных отрезках в прямоугольном треугольнике. Дается представление о методе подобия в задачах на построение. В заключение темы вводятся элементы тригонометрии - синус, косинус и тангенс острого угла прямоугольного треугольника.

Окружность

Взаимное расположение прямой и окружности. Касательная к окружности, ее свойство и признак. Центральные и вписанные углы. Четыре замечательные точки треугольника. Вписанная и описанная окружности.

Цель: расширить сведения об окружности, полученные учащимися в 7 классе; изучить новые факты, связанные с окружностью; познакомить обучающихся с четырьмя заме- чательными точками треугольника. В данной теме вводится много новых понятий и рассматривается много утверждений, связанных с окружностью. Для их усвоения следует уделить большое внимание решению задач. Утверждения о точке пересечения биссектрис треугольника и точке пересечения серединных перпендикуляров к сторонам треугольника выводятся как следствия из теорем о свойствах биссектрисы угла и серединного перпендикуляра к отрезку. Теорема о точке пересечения высот треугольника (или их продолжений) доказывается с помощью утверждения о точке пересечения серединных перпендикуляров. Наряду с теоремами об окружностях, вписанной в треугольник и описанной около него, рассматриваются свойство сторон описанного четырехугольника и свойство углов вписанного четырехугольника.

Повторение. Решение задач

Цель: Повторение, обобщение и систематизация знаний, умений и навыков за курс геометрии 8 класса.

Тематическое планирование

Название темы (раздела)

количество часов

Основное содержание по темам

Характеристика основных видов деятельности

Вводное повторение

2

Начальные геометрические сведения. Параллельные прямые

Признаки равенства треугольников. Задачи на построение

Решать задачи из разделов курса VII класса: формулировать и доказывать признаки и свойства параллельных прямых, призн равенства треуг-ов; соотношения между сторонами и углами треугольника . Характеризовать понятия: теорема, свойство, признак.

Четырехугольники

14

Многоугольник, выпуклый ногоугольник, четырехугольник. Параллелограмм, его свойства и признаки. Трапеция. Прямоугольник, ромб, квадрат, их свойства. Осевая и центральная симметрии.

Формулировать определения

параллелограмма, прямоугольника,

квадрата, ромба, трапеции, равнобедренной

и прямоугольной трапеции, средней линии

трапеции; распознавать и изображать их

на чертежах и рисунках.

Формулировать и доказывать теоремы о

свойствах и признаках параллелограмма,

прямоугольника, квадрата, ромба, трапеции.

Решать задачи на построение,

доказательство и вычисления.

Моделировать условие задачи с помощью

чертежа или рисунка, проводить

дополнительные построения в ходе

решения. Выделять на чертеже

конфигурации, необходимые для

проведения обоснований логических шагов

решения. Интерпретировать полученный

результат и сопоставлять его с условием

задачи

Площадь

14

Понятие площади многоугольника. Площади прямоугольника, параллелограмма, треугольника, трапеции. Теорема Пифагора.

Формулировать и доказывать теорему

Пифагора и обратную ей.

Выводить формулы площадей прямоугольника, параллелограмма, треугольника и трапеции.

Находить площадь многоугольника

разбиением на треугольники четырехугольники.

Объяснять и иллюстрировать отношение

площадей подобных фигур.

Решать задачи на вычисление площадей

треугольников, четырехугольников и

многоугольников. Опираясь на данные

условия задачи, находить возможности

применения необходимых формул,

преобразовывать формулы. Использовать

формулы для обоснования доказательных

рассуждений в ходе решения.

Интерпретировать полученный результат

и сопоставлять его с условием задачи

Подобные треугольники

19

Подобные треугольники. Признаки подобия треугольников. Применение подобия к доказательству теорем и решению задач. Синус, косинус и тангенс острого угла прямоугольного треугольника.

Формулировать определение подобных

треугольников.

Формулировать и доказывать теоремы о

признаках подобия треугольников, теорему

Фалеса.

Формулировать определения и иллюстрировать понятия синуса, косинуса,

тангенса и котангенса острого угла

прямоугольного треугольника. Выводить

формулы, выражающие функции угла

прямоугольного треугольника через его стороны.

Формулировать определения синуса, косинуса, тангенса, котангенса углов от 0 до

180°. Выводить формулы, выражающие

функции углов от 0 до 180° через функции

острых углов. Формулировать и

разъяснять основное тригонометрическое

тождество. По значениям одной тригонометрической функции угла вычислять

значения других тригонометрических функций этого угла.

Решать задачи на построение, доказательство и вычисления. Выделять в условии задачи условие и заключение.

Моделировать условие задачи с помощью

чертежа или рисунка, проводить дополнительные построения в ходе решения. Опираясь на данные условия задачи, проводить необходимые рассуждения. Интерпретировать полученный результат и сопоставлять его с условием задачи

Окружность

15

Взаимное расположение прямой и окружности. Касательная к окружности, ее свойство и признак. Центральные и вписанные углы. Четыре замечательные точки треугольника. Вписанная и описанная окружности.

Формулировать определения понятий,

связанных с окружностью, центрального и

вписанного углов, секущей и касательной к

окружности, углов, связанных с окружностью.

Формулировать и доказывать теоремы о

вписанных углах, углах, связанных с окружностью.

Формулировать соответствие между величиной центрального угла и длиной дуги

окружности.

Изображать, распознавать и описывать

взаимное расположение прямой и окружности.

Решать задачи на вычисление линейных величин, градусной меры угла.

Решать задачи на построение, доказательство и вычисления.

Моделировать условие задачи с помощью

чертежа или рисунка, проводить дополнительные построения в ходе решения. Выделять на чертеже конфигурации, необходимые для проведения обоснований логических шагов решения.

Интерпретировать полученный результат

и сопоставлять его с условием задачи

Повторение

2

Повторение по темам «Четырехугольники», «Площадь», «Подобные треугольники»

Знать материал, изученный в курсе математики за 8 класс.

Владеть общим приемом решения задач.

Уметь применять полученные знания на практике.

Уметь логически мыслить, отстаивать свою

точку зрения и выслушивать мнение других,

работать в команде.

Календарно-тематическое планирование

№

Дата

Тема урока

раздел

Кол-во часов

Оборудование

Основные виды учебной деятельности

Требования к результату

Виды контроля

1

2.09

Треугольники

Повторение

1

Компьютер-проектор

доска

треугольник

транспортир

циркуль

линеика

Решать задачи из разделов курса VII класса: признаки равенства треугольников; соотношения между сторонами и углами треугольника

фронтальный опрос

2

4.09

Параллельные прямые

1

Компьютер-проектор

доска

Решать задачи по теме признаки и свойства параллельных прямых.

фронтальный опрос

I

1. Четырехугольники (14 ч).

3

9.09

Многоугольник. Выпуклый многоугольник Четырехугольник

Ч

Е

Т

Ы

Р

Е

Х

У

Г

О

Л

Ь

Н

И

К

И

2

Компьютер-проектор

доска

треугольник

транспортир

циркуль

линеика

Объяснять , что такое многоугольник, периметр многоугольника, выпуклый многоугольник, четырёхугольник

Знать -

- определение многоугольника и четырёхугольника и их элементов

-утверждение о сумме углов выпуклого многоугольника

- определение и признаки параллелограмма,

-свойство противолежащих углов и сторон параллелограмма,

- свойство диагоналей параллелограмма,

-определение трапеции, равнобокой и прямоугольной трапеции

уметь -

-изображать

многоугольники и четырёхугольники, называть по рисунку их элементы: диагонали, вершины, стороны, соседние и противоположные вершины и стороны,

- применять полученные знания в ходе решения задач

-воспроизводить доказательства признаков и свойств параллелограмма и трапеции и применять их при решении задач

Уметь доказывать свойства и признаки и применять их при решении задач уметь выполнять деление отрезка на n равных частей с помощью циркуля и линейки , уметь выполнять задачи на построение четырехугольников .

Проверка домашнего задания

фронтальный опрос

4

11.09

Многоугольник. Выпуклый многоугольник Четырехугольник

Компьютер-проектор

доска

треугольник

транспортир

циркуль

линеика

Называть элементы многоугольника, вывести формулу суммы углов выпуклого многоугольника, находить углы многоугольников, их периметры.

фронтальный опрос

5

16.09

Параллелограмм

1

Компьютер-проектор

доска

треугольник

транспортир

циркуль

линеика

таблица

Знать определение параллелограмма Формулировать и доказывать теоремы:

- свойство диагоналей параллелограмма;

- свойство противолежащих сторон и углов параллелограмма;

Решать задачи по теме

фронтальный опрос

6

18.09

Признаки параллелограмма

1

Компьютер-проектор

доска

треугольник

транспортир

циркуль

линеика

таблица

Формулировать и доказывать признаки параллелограмма;

применять их при решении

задач

фронтальный опрос индивидуальная работа у доски

7

23.09

Признаки параллелограмма

1

Компьютер проектор

доска

треугольник

транспортир

Признаки параллелограмма;

применять при решении

задач

индивидуальная работа по карточкам

8

25.09

Трапеция

1

Компьютер-проектор

доска

треугольник

транспортир

циркуль

линеика

таблица

Формулировать определение трапеции, виды трапеций, свойство трапеции,

Применять при решении

задач

фронтальный опрос индивидуальная работа у доски

9

30.09

Параллелограмм Трапеция

1

Компьютер-проектор

доска

треугольник

транспортир

циркуль

линеика

Применять при решении

задач знания свойств и признаков параллелограмма

фронтальный опрос индивидуальная работа у доски

10

2.10

Прямоугольник.

1

Компьютер-проектор

доска

чертежные инструменты

Формулировать определение прямоугольника, его свойств и признаков.

Доказывать изученные теоремы и применять их при решении задач

фронтальный опрос индивидуальная работа у доски

11

7.10

Ромб , квадрат

1

Компьютер-проектор

доска

чертежные инструменты

Формулировать определение ромба и квадрата, его свойств и признаков.

Доказывать изученные теоремы и применять их при решении задач

фронтальный опрос индивидуальная работа у доски

12

9.10

Решение задач Прямоугольник, ромб, квадрат

1

Компьютер-проектор

доска

чертежные инструменты Карточки

Доказывать изученные теоремы и применять их при решении задач

Математический диктант

13

14.10

Решение задач по теме «Параллелограмм»

1

Компьютер-проектор

доска

чертежные инструменты

Решать задачи на вычисление, доказательство и построение, используя изученные признаки, свойства и теоремы

Самостоятельная работа

14

16.10

Осевая и центральная симметрия.

1

Компьютер-проектор

доска

чертежные инструменты

Формировать определения симметричных точек и фигур относительно прямой и точки.

Строить симметричные точки и распознавать фигуры, обладающие осевой симметрией и центральной симметрией.

фронтальный опрос индивидуальная работа у доски

15

21.10

Решение задач» Параллелограммы»

1

Компьютер-проектор

доска

чертежные инструменты, Карточки

Решать задачи, опираясь на изученные свойства

Теоретический тест

16

23.10

Контрольная работа № 1 «Четырехугольники»

1

Применять все изученные формулы и теоремы при решении задач

II

Площади фигур (14 ч).

Знать:

- формулы для вычисления площадей параллелограмма, треугольника, трапеции, прямоугольника

- формулировки и доказательства теоремы Пифагора

Уметь:

- применять изученные формулы и теоремы в решении задач

- в устной форме доказывать теоремы и излагать необходимый теоретический материал

- закрепить в процессе решения задач ЗУН

17

28.10

Площадь многоугольника

П

Л

О

Щ

А

Д

И

Ф

И

Г

У

Р

1

Компьютер-проектор

доска

чертежные инструменты, таблица

Объяснять, что такое площадь;

основные свойства площадей и формулу для вычисления площади прямоугольника

Работа у доски , работа с учебником

18

30.10

Площадь прямоугольника

1

Компьютер-проектор

доска

чертежные инструменты

Вывести формулу для вычисления площади прямоугольника и использовать ее при решении задач

фронтальный опрос индивидуальная работа у доски

19,

11.11

Площадь параллелограмма

1

Компьютер-проектор

доска

чертежные инструменты

Вывести формулы для вычисления площади параллелограмма Доказывать и применять все изученные формулы при решении задач

фронтальный опрос индивидуальная работа у доски

20

13.11

Площадь параллелограмма

1

Компьютер-проектор

доска

чертежные инструменты

Доказывать и применять все изученные формулы при решении задач

фронтальный опрос индивидуальная работа у доски

21

18.11

Площадь треугольника

1

Компьютер-проектор

доска

чертежные инструменты

таблица

Вывести формулы для вычисления площади треугольника, теорему об отношении площадей треугольников, имеющих по равному углу

Доказывать их и применять все изученные формулы при решении задач

фронтальный опрос индивидуальная работа у доски

22

20.11

Теорема об отношении площадей треугольника , имеющих по равному углу

1

Компьютер-проектор

доска

чертежные инструменты

Вывести, теорему об отношении площадей треугольников, имеющих по равному углу

Доказывать их и применять все изученные формулы при решении задач

фронтальный опрос индивидуальная работа у доски

23

25.11

Площадь треугольника. Решение задач

1

Компьютер-проектор

доска

чертежные инструменты

Доказывать и применять все изученные формулы при решении задач.

фронтальный опрос индивидуальная работа по карточкам

24

27.11

Площадь трапеции

1

Компьютер-проектор

доска

чертежные инструменты

Вывести формулу для вычисления площади трапеции,

её доказывать и применять при решении задач

фронтальный опрос индивидуальная работа у доски

25

2.12

Площадь трапеции

1

Компьютер-проектор

доска

чертежные инструменты

Выводить формулу для вычисления площади трапеции, и применять при решении задач

Самостоятельная работа

26

4.12

Теорема Пифагора

1

Компьютер-проектор

доска

чертежные инструмент, таблица

Формулировать и доказывать:

теорему Пифагора и применять их при решении задач (находить неизвестную величину в прямоугольном треугольнике)

фронтальный опрос индивидуальная работа у доски

27

9.12

Теорема , обратная теореме Пифагора

1

Компьютер-проектор

доска

чертежные инструменты

Формулировать и доказывать:

теорему Пифагора и применять их при решении задач (находить неизвестную величину в прямоугольном треугольнике)

фронтальный опрос индивидуальная работа у доски

28

11.12

Теорема Пифагора , решение задач.

1

Компьютер-проектор

доска

чертежные инструменты

Формулировать и доказывать:

теорему Пифагора и применять их при решении задач (находить неизвестную величину в прямоугольном треугольнике)

фронтальный опрос индивидуальная работа у доски

тест

29

16.12

Теорема Пифагора, решение задач.

1

Компьютер-проектор

доска

чертежные инструменты

Формулировать и доказывать:

теорему Пифагора и применять их при решении задач (находить неизвестную величину в прямоугольном треугольнике)

Самостоятельная работа

30

18.12

Контрольная работа № 2 «Площадь»

1

применять все изученные формулы и теоремы при решении задач

III

Подобные треугольники (19ч).

31

23.12

Пропорциональные отрезки. Определение подобных треугольников.

П

О

Д

О

Б

Н

Ы

Е

Т

Р

Е

У

Г

О

Л

Ь

Н

И

К

И

1

Компьютер-проектор

доска

чертежные инструменты

таблица

Объяснять, что такое:

- преобразование подобия, коэффициент подобия, подобные фигуры;

Признаки подобия треугольников , отношения пропорциональных отрезков. Знать отношения периметров и площадей.

- определение средней линии треугольника,

- формулировка теоремы о средней линии треугольника,

- пропорциональные отрезки в прямоугольном треугольнике

- определение синуса, косинуса и тангенса острого угла прямоугольного треугольника,

- основное тригонометрическое тождество,

- значения синуса, косинуса и тангенса углов 30⁰, 45⁰ и 60⁰

- основное тригонометрическое тождество,

- значения синуса, косинуса и тангенса углов 30⁰, 45⁰ и 60⁰

Уметь -

Применять все изученные теоремы и формулы , значения синуса , косинуса и тангенса , метрические отношения при решении задач.

фронтальный опрос индивидуальная работа у доски

32

25.12

Отношение площадей подобных треугольников

1

Компьютер-проектор

доска

чертежные инструменты

Доказывать теорему об отношении площадей подобных треугольников и свойство биссектрисы треугольника

Находить неизвестные величины из пропорциональных отношений, применять теорию при решении задач

фронтальный опрос индивидуальная работа у доски

33

13.01

Признаки подобия треугольников . Первый признак подобия

1

Компьютер-проектор

доска

чертежные инструменты

Формулировать и доказывать 1 признак подобия треугольников

и применять его при решении задач

фронтальный опрос индивидуальная работа у доски

34

15.01

Второй признак подобия

1

Компьютер-проектор

доска

чертежные инструменты

Формулировать и доказывать 2 признак подобия треугольников

и применять его при решении задач

фронтальный опрос индивидуальная работа у доски

35

20.01

Третий признак подобия

Компьютер-проектор

доска

чертежные инструменты

Формулировать и доказывать 3 признак подобия треугольников

и применять его при решении задач

фронтальный опрос индивидуальная работа у доски

36

22.01

Решение задач по теме «Признаки подобия»

1

Компьютер-проектор

доска

чертежные инструменты

Применять все изученные формулы и теоремы при решении задач

фронтальный опрос индивидуальная работа у доски

теретический тест

37

27.01

Решение задач по теме «Признаки подобия»

1

Компьютер-проектор

доска

чертежные инструменты

Применять все изученные формулы и теоремы при решении задач

Самостоятельная работа

38

29.01

Контрольная работа № 3 «Признаки подобия треугольников»

1

Применять все изученные формулы и теоремы при решении задач

39

3.02

Средняя линия треугольника

1

Компьютер-проектор

доска

чертежные инструменты

Формулировать и доказывать теорему о средней линии треугольника и применять при решении задач

фронтальный опрос индивидуальная работа у доски

40

5.02

Средняя линия треугольника

1

Компьютер-проектор

доска

чертежные инструменты

Формулировать и доказывать теорему о средней линии треугольника и применять при решении задач

фронтальный опрос индивидуальная работа у доски

41

10.02

Пропорциональные отрезки в прямоугольном треугольнике

1

Компьютер-проектор

доска

чертежные инструменты

Формулировать и доказывать теоремы о точке пересечения медиан треугольника и пропорциональных отрезках в прямоугольном треугольнике и применять при решении задач

фронтальный опрос индивидуальная работа у доски

42

12.02

Пропорциональные отрезки в прямоугольном треугольнике

1

Компьютер-проектор

доска

чертежные инструменты

Формулировать и доказывать теоремы о точке пересечения медиан треугольника и пропорциональных отрезках в прямоугольном треугольнике и применять при решении задач

фронтальный опрос индивидуальная работа с карточками

43,

17.02

Практические приложения подобия треугольников. О подобии произвольных фигур

1

Компьютер-проектор

доска

чертежные инструменты

С помощью циркуля и линейки делить отрезок в данном отношении и решать задачи на построение

фронтальный опрос индивидуальная работа у доски

44

19.02

Практические приложения подобия треугольников. О подобии произвольных фигур

1

Компьютер-проектор

доска

чертежные инструменты

С помощью циркуля и линейки делить отрезок в данном отношении и решать задачи на построение

фронтальный опрос индивидуальная работа у доски

45

24.02

Синус, косинус и тангенс острого угла прямоугольного треугольника

1

Компьютер-проектор

доска

чертежные инструменты

таблица

Объяснять, что такое синус, косинус и тангенс острого угла прямоугольного треугольника

фронтальный опрос индивидуальная работа у доски

46

26.02

Синус, косинус и тангенс острого угла прямоугольного треугольника

1

Компьютер-проектор

доска

чертежные инструменты

Решать задачи на нахождение синуса, косинуса и тангенса острого угла прямоугольного треугольника

Математический диктант

47

3.03

Значения синуса, косинуса, тангенса углов 30 ,45 ,60 .

1

Компьютер-проектор

доска

чертежные инструменты

Знать значения синуса, косинуса и тангенса для углов 30, 45 и 60, метрические соотношения

фронтальный опрос индивидуальная работа у доски

48

5.03

Контрольная работа № 4 «Применение подобия к доказательству теорем и решению задач»

1

Применять все изученные формулы и теоремы при решении задач

49

10.03

Обобщающий урок по теме «Подобие»

1

Компьютер-проектор

доска

чертежные инструменты

Применять все изученные формулы и теоремы при решении задач

фронтальный опрос индивидуальная работа у доски

IV

1. Окружность (15 ч).

50

12.03

Взаимное расположение прямой и окружности

О

К

Р

У

Ж

Н

О

С

Т

Ь

1

Компьютер-проектор

доска

чертежные инструменты

Исследовать возможные случаи взаимного расположения прямой и окружности ,применять при решении задач

Знать определения касательной, точки касания, отрезков касательных, проведенных из одной точки; центрального и вписанного углов, серединного перпендикуляра, вписанной и описанной окружностей; свойство касательной и ее признак; свойства отрезков касательных, проведенных из одной точки, теорему о вписанном угле и ее следствия; теорему об отрезках пересекающихся хорд, свойство биссектрисы угла и его следствия, теорему о серединном перпендикуляре, теорему о точке пересечения высот треугольника; теоремы об окружностях: вписанной в треугольник и описанной около треугольника; свойства описанного и вписанного четырехугольников.

Уметь решать задачи по теме

фронтальный опрос индивидуальная работа у доски

51

17.03

Касательная к окружности.

1

Компьютер-проектор

доска

чертежные инструменты

таблица

Формулировать определение касательной, свойство и признак касательной

Доказывать и применять при решении задач, выполнять задачи на построение окружностей и касательных, определять отрезки хорд окружностей.

фронтальный опрос индивидуальная работа у доски

52

19.03

Касательная к окружности.

1

Компьютер-проектор

доска

чертежные инструменты

таблица

Формулировать определение касательной, свойство и признак касательной,

применять знания при решении задач, выполнять задачи на построение окружностей и касательных, определять отрезки хорд окружностей.

фронтальный опрос индивидуальная работа у доски

опрос теории

53

31.03

Градусная мера дуги окружности.

1

Компьютер-проектор

доска

чертежные инструменты

Объяснять, какой угол называется центральным и какой вписанным, как определяется градусная мера дуги

окружности

Применять при решении задач

фронтальный опрос индивидуальная работа у доски

54

2.04

Теорема о вписанном угле.

1

Компьютер-проектор

доска

чертежные инструменты

Формулировать теорему о вписанном угле, следствия из нее и теорему о произведении отрезков пересекающихся хорд.

Доказывать эти теоремы и применять при решении задач

фронтальный опрос индивидуальная работа у доски

работа с карточками

55

7.04

Теорема о вписанном угле.

1

Компьютер-проектор

доска

чертежные инструменты

Формулировать теорему о вписанном угле,

Доказывать эти теоремы и применять при решении задач

фронтальный опрос индивидуальная работа у доски

56

9.04

Свойство биссектрисы угла .

2

Компьютер-проектор

доска

чертежные инструменты

Знать теорему о биссектрисе угла и следствия

Доказывать теоремы теоремы о биссектрисе угла применять ее при решении задач, выполнять построение замечательных точек треугольника.

фронтальный опрос индивидуальная работа у доски

57

14.04

Свойство серединного перпендикуляра к отрезку.

Компьютер-проектор

доска

чертежные инструменты

Доказывать теоремы теорему о серединном перпендикуляре к отрезку, их следствия и применять их при решении задач, выполнять построение замечательных точек треугольника.

фронтальный опрос индивидуальная работа у доски

58

16.04

Теорема о пересечении высот треугольника

1

Компьютер-проектор

доска

чертежные инструменты

Доказывать теорему и применять при решении задач, выполнять построение замечательных точек треугольника.

фронтальный опрос индивидуальная работа у доски

тест

59,

21.04

Вписанная окружность

1

Компьютер-проектор

доска

чертежные инструменты

таблица

Объяснять, какая окружность называется вписанной в многоугольник, теорему об окружности, вписанной в треугольник, свойства описанного четырехугольника

фронтальный опрос индивидуальная работа у доски

60

23.04

Вписанная окружность

1

Компьютер-проектор

доска

чертежные инструменты

Доказывать теорему и применять при решении задач

фронтальный опрос индивидуальная работа у доски

61

28.04

Описанная окружность

1

Компьютер-проектор

доска

чертежные инструменты

таблица

Объяснять, какая окружность называется описанной около многоугольника, теорему об окружности, описанной около треугольника, свойства вписанного четырехугольника.

фронтальный опрос индивидуальная работа у доски

62

30.04

Описанная окружность

1

Компьютер-проектор

доска

чертежные инструменты

Доказывать теорему об описанной окружности и применять при решении задач

фронтальный опрос индивидуальная работа у доски

63

5.05

Решение задач по теме «Окружность»

1

Компьютер-проектор

доска

чертежные инструменты

- определять градусную меру центрального и вписанного угла;

- решать задачи с использованием замечательных точек треугольника;

фронтальный опрос индивидуальная работа у доски

64

7.05

Контрольная работа № 5 «Окружность»

1

Применять все изученные формулы и теоремы при решении задач

Повторение 5ч.

65

12.05

Решение задач Четырехугольники

1

Компьютер-проектор

доска

чертежные инструменты

Решать задачи по теме «Четырехугольники»

знать наиболее важные виды четырехугольников их свойства;

уметь находить площади многоугольников;

знать теорему Пифагора, уметь применять ее при решении задач;

знать признаки подобия треугольников, уметь применять их при решении

задач;

уметь находить значения синуса, косинуса и тангенса острого угла

прямоугольного треугольника;

знать случаи взаимного расположения прямой и окружности, свойство и

признак касательной к окружности, о четырех замечательных точках

треугольника;

иметь представление о вписанной и описанной окружностях.

фронтальный опрос индивидуальная работа у доски

66

14.05

Решение задач Четырехугольники

1

Компьютер-проектор

доска

чертежные инструменты

Решать задачи по теме «Четырехугольники»

фронтальный опрос индивидуальная работа у доски

самостоятельная работа

67

19.05

Решение задач «Площади»

1

Компьютер-проектор

доска

чертежные инструменты

Решать задачи по теме «Площади»

фронтальный опрос индивидуальная работа у доски

тест

68

21.05

Решение задач «Подобие»

1

Компьютер-проектор

доска

чертежные инструменты

Решать задачи по теме «Подобие»

тест

69

26.05

Итоговая контрольная работа

1

Компьютер-проектор

доска

чертежные инструменты

Применять все изученные формулы и теоремы при решении задач

70

28.05

Решение задач

Решать задачи по всем темам курса геометрии 8 класса

С/р

ПЕРЕЧЕНЬ контрольных работ

№ урока

Вид контроля

Тема

Дата проведения

16

Контрольная работа

Четырехугольники

23.10

30

Контрольная работа

Площадь

18.12

38

Контрольная работа

Признаки подобия треугольников

29.01

48

Контрольная работа

Применение подобия к доказательству теорем и решению задач

5.03

64

Контрольная работа

Окружность

7.05

69

Контрольная работа

Итоговая

26.05

Результаты освоения учебного предмета и система их оценки

Результаты обучения представлены в Требованиях к уровню подготовки учащихся, примерных текстах контрольных работ по курсу геометрии за 8 класс и задают систему итоговых результатов обучения, достижение которых является обязательным условием положительной аттестации ученика за курс.

Планируемые результаты

должны знать:

Определение многоугольника, четырёхугольника, параллелограмма, трапеции, ромба, прямоугольника, квадрата. Свойства и признаки данных геометрических фигур. Формулы для нахождения площадей фигур. Теорему Пифагора. Признаки подобия треугольников. Определение синуса, косинуса, тангенса прямоугольного треугольника, соотношение между сторонами и углами прямоугольного треугольника. Центральные и вписанные углы. Четыре замечательные точки треугольника. Свойства биссектрисы угла и серединного перпендикуляра к отрезку. Теорему о пересечении высот треугольника, а также теоремы о вписанной и описанной окружностях.

должны уметь:

Вычислять сумму внутренних углов многоугольника. Решать задачи с использованием свойств геометрических фигур. Находить площади параллелограмма, прямоугольника, трапеции, ромба. Использовать теорему Пифагора для определения сторон прямоугольного треугольника. Решать задачи с использованием признаков подобия треугольников. Вычислять элементы прямоугольного треугольника, используя тригонометрические функции. Решать задачи по теме окружность, центральные и вписанные углы, вписанные и описанные окружности.

владеть компетенциями:

познавательной, коммуникативной, информационной и рефлексивной.

способны решать следующие жизненно-практические задачи:

Самостоятельно приобретать и применять знания в различных ситуациях, работать в группах, аргументировать и отстаивать свою точку зрения, уметь слушать других, извлекать учебную информацию на основе сопоставительного анализа объектов, пользоваться предметным указателем энциклопедий и справочником для нахождения информации, самостоятельно действовать в ситуации неопределённости при решении актуальных для них проблем.

Критерии оценок по математике

Рекомендации по оценке знаний и умений учащихся по математике

Опираясь на эти рекомендации, учитель оценивает знания и умения учащихся с учетом их индивидуальных особенностей.

1. Содержание и объем материала, подлежащего проверке, определяется программой. При проверке усвоения материала нужно выявлять полноту, прочность усвоения учащимися теории и умения применять ее на практике в знакомых и незнакомых ситуациях.

2. Основными формами проверки знаний и умений учащихся по математике являются письменная контрольная работа и устный опрос.

При оценке письменных и устных ответов учитель в первую очередь учитывает показанные учащимися знания и умения. Оценка зависит также от наличия и характера погрешностей, допущенных учащимися.

1. Среди погрешностей выделяются ошибки и недочеты. Погрешность считается ошибкой, если,она свидетельствует о том, что ученик не овладел основными знаниями, умениями, указанными впрограмме

К недочетам относятся погрешности, свидетельствующие о недостаточно полном или недостаточно прочном усвоении основных знаний и умений или об отсутствии знаний, не считающихся в программе основными. Недочетами также считаются: погрешности, которые не привели к искажению смысла полученного учеником задания или способа его выполнения; неаккуратная запись; небрежное выполнение чертежа.

Граница между ошибками и недочетами является в некоторой степени условной. При одних обстоятельствах допущенная учащимися погрешность может рассматриваться учителем как ошибка, в другое время и при других обстоятельствах - как недочет.

4. Задания для устного и письменного опроса учащихся состоят из теоретических вопросов и задач.Ответ на теоретический вопрос считается безупречным, если по своему содержанию полностью соответствует вопросу, содержит все необходимые теоретические факты я обоснованные выводы, а его изложение и письменная запись математически грамотны и отличаются последовательностью и аккуратностью.

Решение задачи считается безупречным, если правильно выбран способ решения, само решение сопровождается необходимыми объяснениями, верно выполнены нужные вычисления и преобразования, получен верный ответ, последовательно и аккуратно записано решение.

5. Оценка ответа учащегося при устном и письменном опросе проводится по пятибалльной системе, т. е. за ответ выставляется одна из отметок: 1 (плохо), 2 (неудовлетворительно), 3 (удовлетворительно), 4 (хорошо), 5 (отлично).

6. Учитель может повысить отметку за оригинальный ответ на вопрос или оригинальное решение задачи, которые свидетельствуют о высоком математическом развитии учащегося; за решение более сложной задачи или ответ на более сложный вопрос, предложенные учащемуся дополнительно после выполнения им заданий.

Критерии ошибок

К грубым ошибкам относятся ошибки, которые обнаруживают незнание учащимися формул, правил, основных свойств, теорем и неумение их применять; незнание приемов решения задач, рассматриваемых в учебниках, а также вычислительные ошибки, если они не являются опиской;

К негрубым ошибкам относятся: потеря корня или сохранение в ответе постороннего корня; отбрасывание без объяснений одного из них и равнозначные им;

К недочетам относятся: нерациональное решение, описки, недостаточность или отсутствие пояснений, обоснований в решениях

Оценка устных ответов учащихся

Ответ оценивается отметкой «5», если ученик:

полно раскрыл содержание материала в объеме, предусмотренном программой и учебником,

изложил материал грамотным языком в определенной логической последовательности, точноиспользуя математическую терминологию и символику;

правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;

показал умение иллюстрировать теоретические положения конкретными примерами,применять их в новой ситуации при выполнении практического задания;

продемонстрировал усвоение ранее изученных сопутствующих вопросов, сформированность11и устойчивость используемых при отработке умений и навыков;

отвечал самостоятельно без наводящих вопросов учителя. Возможны одна - две неточностипри освещении второстепенных вопросов или в выкладках, которые ученик легко исправил по замечанию учителя.

Ответ оценивается отметкой «4», если он удовлетворяет в основном требованиям на оценку «5», но при этом имеет один из недостатков:

в изложении допущены небольшие пробелы, не исказившие математическое содержание ответа;

допущены один - два недочета при освещении основного содержания ответа, исправленные по замечанию учителя;

допущены ошибка или более двух недочетов при освещении второстепенных вопросов или в выкладках, легко исправленные по замечанию учителя.

Отметка «3» ставится в следующих случаях:

неполно или непоследовательно раскрыто содержание материала, по показано общее понимание вопроса и продемонстрированы умения, достаточные для дальнейшего усвоения программного материала (определенные «Требованиями к математической подготовке учащихся»);

имелись затруднения или допущены ошибки в определении понятий, использовании математической терминологии, чертежах, выкладках, исправленные после нескольких

наводящих вопросов учителя;

ученик не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме;

при знании теоретического материала выявлена недостаточная сформированность основных умений и навыков.

Отметка «2» ставится в следующих случаях:

не раскрыто основное содержание учебного материала;

обнаружено незнание или непонимание учеником большей или наиболее важной части учебного материала;

допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов учителя.

Отметка «1» ставится, если:

ученик обнаружил полное незнание и непонимание изучаемого учебного материала или не смог ответить ни на один из поставленных вопросов по изучаемому материалу.

Оценка письменных работ учащихся

Отметка «5» ставится, если:

работа выполнена полностью;

в логических рассуждениях и обосновании решения нет пробелов и ошибок; •S в решении нет математических ошибок (возможна одна неточность, описка, не являющаяся следствием незнания или непонимания учебного материала).

Отметка «4» ставится, если:

работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);

допущена одна ошибка или два-три недочета в выкладках, рисунках, чертежах или графиках (если эти виды работы не являлись специальным объектом проверки).

Отметка «3» ставится, если:

допущены более одной ошибки или более двух-трех недочетов в выкладках, чертежах или графиках, но учащийся владеет обязательными умениями по проверяемой теме.

Отметка «2» ставится, если:

допущены существенные ошибки, показавшие, что учащийся не владеет обязательными умениями по данной теме в полной мерс.

Отметка «1» ставится, если:

работа показала полное отсутствие у учащегося обязательных знаний и умений по проверяемой теме или значительная часть работы выполнена не самостоятельно.

Перечень учебно-методического и материально-технического обеспечения

Для учащихся:

Учебник «Геометрия, 7-9», авторы Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др.

Для учителя:

1. Геометрия: учебник для 7-9 кл. / Л. С. Атанасян, В. Ф. Бутузов, С. В. Кадомцев и др.- М.: Просвещение, 2011.

2. Изучение геометрии в 7, 8, 9 классах: метод, рекомендации: кн. для учителя / [Л.С. Атанасян, В.Ф. Бутузов, Ю.А. Глазков и др.]. - М.: Просвещение, 2010.

3. Гусев В. А. Геометрия: дидакт. материалы для 8 кл. / В.А. Гусев, А.И. Медяник. - М.: Просвещение, 2010.

4. Зив Б.Г. Геометрия: Дидактические материалы для 8 кл. / Б.Г. Зив, В.М. Мейлер. - М.: Просвещение, 2010.

5. Гаврилова Н.Ф. Поурочные разработки по геометрии. 8 класс. М.: ВАКО, 2010 - (В помощь школьному учителю)

Печатные пособия

1. Демонстрационный материал в соответствии с основными темами программы обучения:

• Теорема Пифагора

• Синус, косинус и тангенс острого угла прямоугольного треугольника

• Подобие треугольников

• Формула площади треугольников

• Свойства параллелограмма

• Трапеция

• Признаки параллелограмма

• Теорема Фалеса

• Площадь многоугольника

• Окружность. Хорда и касательная

• Окружность, описанная около треугольника

• Окружность, вписанная в треугольник

• Центральные и вписанные углы

2. Карточки с заданиями по математике

3. Портреты выдающихся деятелей математики

Учебно- практическое и учебно- лабораторное оборудование

1. Комплект чертежных инструментов: линейка, транспортир, угольник, циркуль.

2. Комплект планиметрических тел.

Технические средства обучения:

1. Компьютер

2. Мультимедийный проектор

3. Экран

Интернет-сайты

• www.

• www.mathvaz.ru

• www.1september.ru

• www.math.ru

• www.allmath.ru

• www.uztest.ru

КОНТРОЛЬНАЯ РАБОТА № 1 «Четырехугольники» 23.10

Вариант I

1. Диагонали прямоугольника АВСD пересекаются в точке О. Найдите угол между диагоналями, если АВО = 30°.

2. В параллелограмме KМNP проведена биссектриса угла МKР, которая пересекает сторону MN в точке Е.

а) Докажите, что треугольник KМЕ равнобедренный.

б) Найдите сторону KР, если МЕ = 10 см, а периметр параллелограмма равен 52 см.

Вариант II

1. Диагонали ромба KМNP пересекаются в точке О. Найдите углы треугольника KОМ, если угол МNP равен 80°.

2. На стороне ВС параллелограмма АВСD взята точка М так, что АВ = ВМ.

а) Докажите, что АМ - биссектриса угла ВАD.

б) Найдите периметр параллелограмма, если СD = 8 см, СМ = 4 см.

КОНТРОЛЬНАЯ РАБОТА № 2 «Площадь» 18.12

Вариант I

1. Смежные стороны параллелограмма равны 32 см и 26 см, а один из его углов равен 150°. Найдите площадь параллелограмма.

2. Площадь прямоугольной трапеции равна 120 см², а ее высота равна 8 см. Найдите все стороны трапеции, если одно из оснований больше другого на 6 см.

3. На стороне АС данного треугольника АВС постройте точку D так, чтобы площадь треугольника АВD составила одну треть площади треугольника АВС.

Вариант II

1. Одна из диагоналей параллелограмма является его высотой и равна 9 см. Найдите стороны этого параллелограмма, если его площадь равна 108 см².

2. Найдите площадь трапеции АВСD с основаниями АD и ВС, если АВ = 12 см, ВС = 14 см, АD = 30 см, В = 150°.

3. На продолжении стороны KN данного треугольника KМN постройте точку Р так, чтобы площадь треугольника NMP была в два раза меньше площади треугольника KМN.

КОНТРОЛЬНАЯ РАБОТА № 3 «Подобные треугольники» 29.01

Вариант I

1. На рисунке 1 АВ || СD. а) Докажите, что АО : ОС = ВО : ОD. б) Найдите АВ, если ОD = 15 см, ОВ = 9 см, СD = 25 см.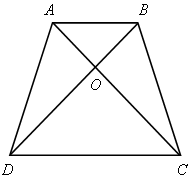

2. Найдите отношение площадей треугольников АВС и KMN, если АВ = 8 см, ВС = 12 см, АС = 16 см, KM = 10 cм, MN = 15 см, NK = 20 см.

Вариант II

1. На рисунке 2 MN || АС. а) Докажите, что АВ · BN = CВ · BM. б) Найдите MN, если AM = 6 см, ВM = 8 см, АС = 21 см.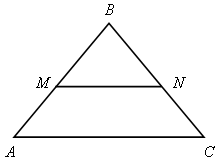

2. Даны стороны треугольников PQR и АВС: PQ = 16 см, QR = 20 см, PR = 28 см и АВ = 12 cм, ВС = 15 см, АС = 21 см. Найдите отношение площадей этих треугольников.

Контрольная работа № 4 5.03

Вариант I

1. В прямоугольном треугольнике АВС А = 90°, АВ = 20 см; высота АD = 12 см. Найдите АС и cos C.

2. Диагональ ВD параллелограмма АВСD перпендикулярна к стороне АD. Найдите площадь параллелограмма АВСD, если АВ = 12 см,
А = 41°.

Вариант II

1. Высота ВD прямоугольного треугольника АВС равна 24 см и отсекает от гипотенузы АС отрезок DС, равный 18 см. Найдите АВ и соs A.

2. Диагональ АС прямоугольника АВСD равна 3 см и составляет со стороной АD угол 37°. Найдите площадь прямоугольника АВСD.

КОНТРОЛЬНАЯ РАБОТА № 5 «Окружность» 7.05

Вариант I

1. Через точку А окружности проведены диаметр АС и две хорды АВ и АD, равные радиусу этой окружности. Найдите углы четырехугольника АВСD и градусные меры дуг АВ, ВС, СD, АD.

2. Основание равнобедренного треугольника равно 18 см, а боковая сторона равна 15 см. Найдите радиусы вписанной в треугольник и описанной около треугольника окружностей.

Вариант II

1. Отрезок ВD - диаметр окружности с центром О. Хорда АС делит пополам радиус ОВ и перпендикулярна к нему. Найдите углы четырехугольника АВСD и градусные меры дуг АВ, ВС, СD, АD.

2. Высота, проведенная к основанию равнобедренного треугольника, равна 9 см, а само основание равно 24 см. Найдите радиусы вписанной в треугольник и описанной около треугольника окружностей.

Итоговая контрольная работа по геометрии 26.05.

8 класс

1 вариант

1. Найдите площадь равнобедренного треугольника со сторонами 10см, 10см и 12 см.

2. В параллелограмме две стороны 12 и 16 см, а один из углов 150°. Найдите площадь параллелограмма.

3. В равнобедренной трапеции боковая сторона равна 13 см, основания 10 см и 20 см. Найдите площадь трапеции.

4. В треугольнике АВС прямая MN , параллельная стороне АС, делит сторону ВС на отрезки BN=15 см и NC=5 см, а сторону АВ на ВМ и АМ. Найдите длину отрезка MN, если АС=15 см.

5. В прямоугольном треугольнике АВС =90°, АС=8 см, =45°. Найдите:

а)АС; б) высоту СD, проведенную к гипотенузе.

6. Дан прямоугольный треугольник АВС, у которого С-прямой, катет ВС=6 см и А=60°. Найдите:

а) остальные стороны ∆АВС

б) площадь ∆АВС

в) длину высоты, опущенной из вершины С.

2 вариант

1. В равнобедренном треугольнике боковая сторона равна 13 см, а высота, проведенная к основанию, 5 см. Найдите площадь этого треугольника.

2. В параллелограмме АВСД АВ=8 см, АД=10 см, 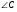=30°. Найдите площадь параллелограмма.

3. В прямоугольной трапеции АВСД боковая сторона равна АВ=10 см, большее основание АД= 18 см, 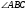=45°. Найдите площадь трапеции.

4. В треугольнике АВС со сторонами АС=12 см и АВ=18 см проведена прямая MN, параллельная АС, MN=9 см. Найдите ВМ.

5. В прямоугольном треугольнике АВС =90°, АС=8 см, =45° . Найдите:

а)АВ; б) высоту СD, проведенную к гипотенузе.

6. Дан прямоугольный треугольник АDС, у которого D-прямой, катет AD=3 см и DАC=30°. Найдите:

а) остальные стороны ∆АDС

б) площадь ∆АDС

в) длину высоты, проведенной к гипотенузе.