- Учителю
- Устный счёт по математике 5 класс
Устный счёт по математике 5 класс
Устный счёт к разделу
«Обыкновенные и десятичные дроби» математика 5 класс
Учитель математики СОШ №34
инновационного типа г.Павлодара
Мукушева Айгуль Хайруллаевна
Павлодар 2014 год
Содержание работы
по теме: «Обыкновенные и десятичные дроби» для 5 класса.
1. Перечень тем …………………………………………………………………. 2
2. Пояснительная записка ………………………………………………………3 - 5
3. Приложение №1 «Запись и чтение обыкновенных и десятичных дробей» … .6
4. Приложение №2 «Сложение и вычитание обыкновенных дробей» ………….7
5. Приложение №3 «Сравнение десятичных дробей» ……………………………8
6. Приложение №4 «Сложение и вычитание десятичных дробей» …………….9
7. Приложение №5 «Изображение обыкновенных дробей на координатном луче» ………………………………………………………………………………..10
8. Приложение №6 «Умножение обыкновенных дробей»………………………11
9. Приложение №7 «Деление обыкновенных дробей» ………………………….12
10. Приложение №8 «Умножение десятичных дробей» ………………………..13
11. Приложение №9 «Деление десятичных дробей» ……………………………14
12. Приложение №10 «Арифметические действия над обыкновенными дробями»…………………………………………………………………………….15
13. Приложение №11 «Арифметические действия над десятичными дробями» ……………………………………………………………………………………….16
14. Использованная литература …………………………………………………..17
«Математику уже затем учить надо, что она ум в порядок приводит».
М.В.Ломоносов.
Пояснительная записка.
Одна из важнейших задач образовательного процесса - развитие у школьников логического мышления. Для осуществления развивающих целей обучения необходимо активизировать познавательную деятельность, создать ситуацию заинтересованности. Целенаправленное, интенсивное развитие логического мышления становится одной из центральных задач обучения, важнейшей проблемой его теории и практики.
Умение мыслить логически, выполнять умозаключение без опоры на наглядность, сопоставлять суждения по определённым правилам - необходимое условие успешного усвоения учебного материала. Главная цель моей работы по развитию логического мышления состоит в том, чтобы дети научились делать выводы из тех суждений, которые им предлагается в качестве исходных. Решение логических задач на уроках математики не только повышает активность учащихся и развивает их мышление, но и в значительной степени вызывает интерес к математике.
Необходимо особенно в среднем звене на уроках математики систематически использовать устный счёт, способствующие целенаправленному развитию логического мышления учащихся, их математическому развитию, формированию у них познавательного интереса и самостоятельности. Такие задания требуют от школьников наблюдательности, творчества и оригинальности.
Логические (мыслительные) действия, дают человеку новое знание. Но важная отличительная их способность в том, что здесь добывается знание о чём-то неявном, скрытом, незримом, недоступном органам чувств.
Развитие логического мышления, в свою очередь, позволяет подрастающей личности адекватно воспринимать окружающуюся действительность, реально оценивать свою роль в происходящих вокруг событиях, выбирать тождественные методы реагирования.
В данной программе создана система знаний, направленных на развитие творческого и логического мышления у младшего школьника, включающую в себя умение наблюдать, сравнивать, обобщать, находить закономерности, строя простейшие предложения, проверять их, делая выводы, иллюстрировать их на примерах.
Цели обучения
Цели обучения математике в общеобразовательном учреждении определяются её ролью в развитии общества в целом и формировании личности каждого отдельного человека.
Без базовой математической подготовки невозможна постановка образования современного человека. В школе математика служит опорным предметом для изучения смежных дисциплин. В послешкольной жизни реальной необходимостью в наши дни становится непрерывное образование, что требует полноценной базовой общеобразовательной подготовки, в том числе и математической. И, наконец, все больше специальностей, требующих высокого уровня образования, связано с непосредственным применением математики (экономика, бизнес, финансы, физика, химия, техника, информатика, биология, психология и многое другое). Таким образом, расширяется круг школьников, для которых математика становится профессионально значимым предметом.
Для жизни в современном обществе важным является формирование математического стиля мышления проявляющегося в определенных умственных навыках. В процессе математической деятельности в арсенал приемов и методов человеческого мышления естественным образом включаются индукция и дедукция, обобщение и конкретизация, анализ и синтез, классификация и систематизация, абстрагирование и аналогия. Объекты математических умозаключений и правила их конструирования вскрывают механизм логических построений, вырабатывают умения формулировать, обосновывать и доказывать суждения, тем самым развивают логическое мышление. Ведущая роль принадлежит математике в формировании алгоритмического мышления, воспитании умений действовать по заданному алгоритму и конструировать новые. В ходе решения задач - основной учебной деятельности на уроках математики - развиваются творческая и прикладная стороны мышления.
Использование в математике наряду с естественным нескольких математических языков дает возможность развивать у учащихся точную, экономную и информативную речь, умение отбирать наиболее подходящие языковые (в частности, символические, графические) средства.
Математическое образование вносит вклад в формирование общей культуры человека. Изучение математики способствует эстетическому воспитанию человека, развивает его воображение, пространственные представления.
Роль математической подготовки в общем образовании современного человека ставит следующие цели обучения математике:
· овладение конкретными математическими знаниями, необходимыми для применения в практической деятельности, для изучения смежных дисциплин, для продолжения образования;
· интеллектуальное развитие учащихся, формирование качеств мышления, характерных для математической деятельности и необходимых для продуктивной жизни в обществе;
· формирование представлений об идеях и методах математики, о математике как форме описания и методе познания действительности;
· формирование представлений о математике как части общечеловеческой культуры, понимания значимости математики для общественного прогресса.
Требования к уровню подготовки учащихся 5 - х классов
Учащиеся должны знать/понимать:
- сущность понятия алгоритма, приводить примеры алгоритмов;
- как используются математические формулы и уравнения, примеры их применения для решения математических и практических задач;
- как потребности практики привели математическую науку к необходимости расширения понятия числа;
- понятия десятичной и обыкновенной дробей, правила выполнения действий с десятичными дробями, обыкновенными дробями с одинаковыми знаменателями, понятие процента;
- понятия «уравнение» и «решение уравнения»;
- смысл алгоритма округления десятичных дробей;
- переместительный, распределительный и сочетательный законы;
- понятие среднего арифметического;
- понятие натуральной степени числа;
- определение прямоугольного параллелепипеда и куба, формулы для вычисления длины окружности и площади круга;
Должны уметь:
- выполнять арифметические действия с десятичными дробями (в том числе устное сложение и вычитание десятичных дробей с двумя знаками);
- выполнять сложение и вычитание обыкновенных дробей, имеющих общий знаменатель;
- переходить от одной формы записи чисел к другой, представлять десятичную дробь в виде обыкновенной и в простейших случаях обыкновенную в виде десятичной, проценты в виде дроби и дробь в виде процентов, округлять целые числа и десятичные дроби;
- выполнять прикидку и оценку значений числовых выражений;
- выполнять действия с числами разного знака;
- пользоваться основными единицами длины, массы, времени, площади, выражать более крупные единицы через мелкие и наоборот;
- находить значения степеней с натуральными показателями;
- решать линейные уравнения;
- изображать числа точками на координатной прямой;
- решать текстовые задачи на дроби и проценты;
- вычислять объемы прямоугольного параллелепипеда и куба, находить длину окружности и площадь круга.
Приложение №1 «Запись и чтение обыкновенных и десятичных дробей»
А) Записать десятичной дробью:
; 
Контроль:
7,5; 0,45; 5,04; 0,9; 0,041; 7,352
Б) Записать числа в виде суммы разрядных слагаемых.
Образец: 2973=2000+900+70+3
4706=
5005=
5900=
20010=
Контроль:
4000+700+6
5000+5
5000+900
20000+10
В) Записать сумму как одно число:
8000 + 700 + 20+9=
6000+400+70+4=
7000+40+2=
Контроль:
8729; 6474; 7042
Приложение № 2 «Сложение и вычитание обыкновенных дробей»
Вариант №1
1. Вычислите:
А) 10
Б) 5
В) 7
Г) 12
Вариант №2
1. Вычислите:
А) 5
Б) 
В) 6
Г) 6
Приложение №3 «Сравнение десятичных дробей»
Вариант 1
1. Сравнить дроби:
18,625 и 5,784
15,200 и 15,200
3,0251 и 21,02
7,65 и 7,8
23,0521 и 0,0521
0,089 и 0,0081
2. Сравните числа, заменив звездочку знаком < или >:
А)1,601*1,599 Г) 10,6*10,599
Б) 3,02*3,019 Д) 4,62*4,5888
В) 8,698*9,001 Е) 0,099*0,81
Вариант 2
1. Сравнить дроби:
0,3 и 0,8
0,90 и 0,9
5,6 и 3,6
2,99 и 13,1
0,759 и 0,76
3,4208 и 3,4028
2. Сравните числа, заменив звездочку знаком < или >:
А) 2,701*2,698 Г) 4,629*4,63
Б) 10,71*10,7 Д) 4,398*4,401
В) 5,03*5,029 Е) 0,012*0,1
Приложение №4 «Сложение и вычитание десятичных дробей»
I Вариант
1. Вычислите устно
1)7,8 + 6,9 =
2) 129 + 9,72=
3) 24,2 + 0,867=
4) 5,8 + 22,1=
5) 2,7 + 1,35 + 0,8=
6) 13,75 + 8,2 +0,11=
Контроль:
1) 14,7 2) 138,72
3) 25,067 4) 27,991
5) 4,85 6) 22,065
2. Деревянную балку длиной 6,85м. разрезать на две части. Длина одной части 2,96м. найдите длину второй части.
II Вариант
Вычислите устно
1) 96,3 - 0,081=
2) 830 - 0, 0097=
3) 6,6 - 5,99=
4) 7,79 - 3,79=
5)9,83 - 1,76 - 3,28 =
6) 14,87 - 5,82 - 3,27=
Контроль :
1) 96,219 2) 829, 9903
3) 0,61 4) 4
5)4,79 6) 5,78
2. Из заготовки цилиндрической формы диаметром 53,6 см. нужно выточить деталь, диаметром 44,1 см. на сколько диаметр новой детали стал меньше диаметра заготовки?
Приложение №5 «Изображение обыкновенных дробей на координатном луче»
Вариант 1
1. Начертите координатный луч, за единичный отрезок примите 9 клеток тетради. Отметьте на координатном луче точки: А(
; В(
, С(1); D(
; Е(1
2. Начертите координатный луч, за единичный отрезок примите 10 клеток тетради. Отметьте на луче точки, которым соответствуют числа: 
1
.
3. Начертите координатный луч, за единичный отрезок примите 12 клеток тетради. Отметьте на координатном луче точку N(1
, отложите точки в обе стороны от точки N на расстоянии 
единичного отрезка. Обозначьте эти точки и укажите их координаты.
Вариант 2
1. Начертите координатный луч, за единичный отрезок примите 7 клеток тетради. Отметьте на координатном луче точки: М(
; В(
, С(2); D(
; Е(1
.
2. Начертите координатный луч, за единичный отрезок примите 6 клеток тетради. Отметьте на луче точки, которым соответствуют числа: 
1
.
3. Начертите координатный луч, за единичный отрезок примите 8 клеток тетради. Отметьте на координатном луче точку N(1
, отложите точки в обе стороны от точки N на расстоянии 
единичного отрезка. Обозначьте эти точки и укажите их координаты.
Приложение №6 «Умножение обыкновенных дробей»
Вариант 1
1. Вычислите:
А) 
Б) 4
В) 1
2. Заполните таблицу:
а
3
1
Вариант 2
1. Вычислите:
А) 
Б) 1
В) 
2. Решите уравнения:
б) 
в) 2
Приложение №7 «Деление обыкновенных дробей»
Вариант 1
1. Сократить дробь: 
;
;
; 
…
2. Обратить в неправильную дробь:
; 5
; 7
…
3. За 
кг конфет заплатили 1 тыс. рублей. Сколько стоят 1 кг таких конфет?
Вариант 2
1. Выполните деление:
А)7:9=
В)7 
2. Обратить в неправильную дробь: 3
3. Площадь прямоугольника 21
2. Его длина 6
Найдите ширину прямоугольника.
Приложение №8 «Умножение десятичных дробей»
Вариант 1
1. Выполните умножение:
4,3
=
8,02
2=
19,7 11=
2. Ребро куба 4,3 см. Найдите сумму длин всех ребер куба.
3. Вычислите:
Вариант 2
1. Выполните умножение:
21,3510=
4,963100=
0,71214=
2. Сторона квадрата 6,5 см. Найдите периметр квадрата.
3. Вычислите:
(1,8+6,24)(1-0,4)=
Приложение №9 «Деление десятичных дробей»
Вариант 1
1. Вычислите:
78,2:17=
45,09:15=
852,6:42=
2. Найдите значение выражений:
356,8:а+7003:в при а=10; в=100
Вариант 2
1. Вычислите:
42,56:38=
2802,8:14=
0,0336:21=
2. Найдите значения выражения:
724,2:а-423,6:в при а= 10; в=100.
Приложение №10 «Арифметические действия над обыкновенными дробями»
Вариант 1
1. Выберите неправильные дроби:
2. Представьте 0,12 в виде обыкновенной несократимой дроби.
3. Сколько килограммов в 2 
центнера?
А) 240 кг Б) 225 кг В) 2400 кг
4. Сравните дроби 
и 
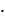
5. Найдите 75% от 60
А) 4500, 0,5 Б) 4,5 В) 45
6. Вычислите: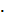 
2:
Приложение №11 «Арифметические действия над десятичными дробями»
Вариант 1
1. Решите уравнения и прочтите:
Х*0,7=49 х:70=1,4 10,5:х=3,5
9,6:х=0,8 1,8*х=7,2 х:1,8=50
Таблица ответов:
3
12
90
4
98
70
75
и
р
т
ф
а
г
к
(ответ: графит)
2. Игра «Знаешь ли ты?»
Великая Отечественная война началась 22 июня 1941 года. Узнать сколько дней продолжалась война поможет следующая цепочка:
5,9*36,1=∆ +0,01=∆:0,03=∆-6958,2=∆*10=∆
Вариант 2
1. На Земном шаре обитают птицы - безошибочные составители прогноза погоды на лето. Название этих птиц зашифровано примерами. Применяя прием последовательного деления, найдите частные: 450:1,8; 31,5:15, 42:28; 36:0,8; 21:0,015; 6:25; 42,5:25; 49:1,4.
Заменив частные буквами, вы прочтете название птиц - метеоритов (ответ: фламинго).
1,5
35
1,7
250
0,24
45
2,1
1400
а
о
г
ф
н
м
л
и
Фламинго из песка строят гнезда в форме усеченного конуса, в верхнем основании делают углубления, в котором откладывают яйца. Высота гнезда зависит от того, какое будет лето. Если лето ожидается дождливым, то гнезда строятся высокими, чтобы их не могла затопить вода; если засушливым - то более низкими.
2. Игра «Знаешь ли ты?»
Великая Отечественная война началась 22 июня 1941 года. Узнать сколько дней продолжалась война поможет следующая цепочка:
6,1*52,1=∆+0,19=∆:0,03=∆-10458,2=∆*10=∆
Использованная литература:
1. Математика 5 класс (Атамұра 2010);
2. Математика - рабочая тетрадь (Атамұра 2010);
3.
4.
18