Конспект урока по алгебре на тему Решение упражнений по теме Функции (7 класс)

7 класс

УРОК № 32. Глава 2. Функции (11 часов)

Тема. Решение упражнений по теме «Функции».

Цель. Обобщить и систематизировать знания учащихся по теме «Функции».

Ход урока.

1. Организационный момент.

2. Проверка домашнего задания.

3. Актуализация опорных знаний.

1. Сформулируйте определение прямой пропорциональности?

2. Что является графиком прямой пропорциональности?

3. Как построить график прямой пропорциональности?

4. В каких четвертях располагается график прямой пропорциональности если k > 0? k < 0?

5. Сформулируйте определение линейной функции.

6. Что является графиком линейной функции?

7. Как построить график линейной функции?

8. Каково может быть взаимное расположение графиков линейных

9. Что является графиком функции у = b?

4. Анализ самостоятельной работы по теме «Построение графиков линейной функции и прямой пропорциональности».

5. Решение упражнений.

1. Функция задана формулой .Определите:

а) значение у, если х = 0,4;

б) значение х, при котором у = 3;

в) проходит ли график функции через точку С(-6; -12).

Решение.

а) х = 0,4, то ;

б) у = 3, то ,

,

.

в) С (-6; -12), то ,

. Значит С (-6; -12) принадлежит графику.

2. а) Постройте график функции ;

б) Укажите с помощью графика, чему равно значение у при х = -1,5.

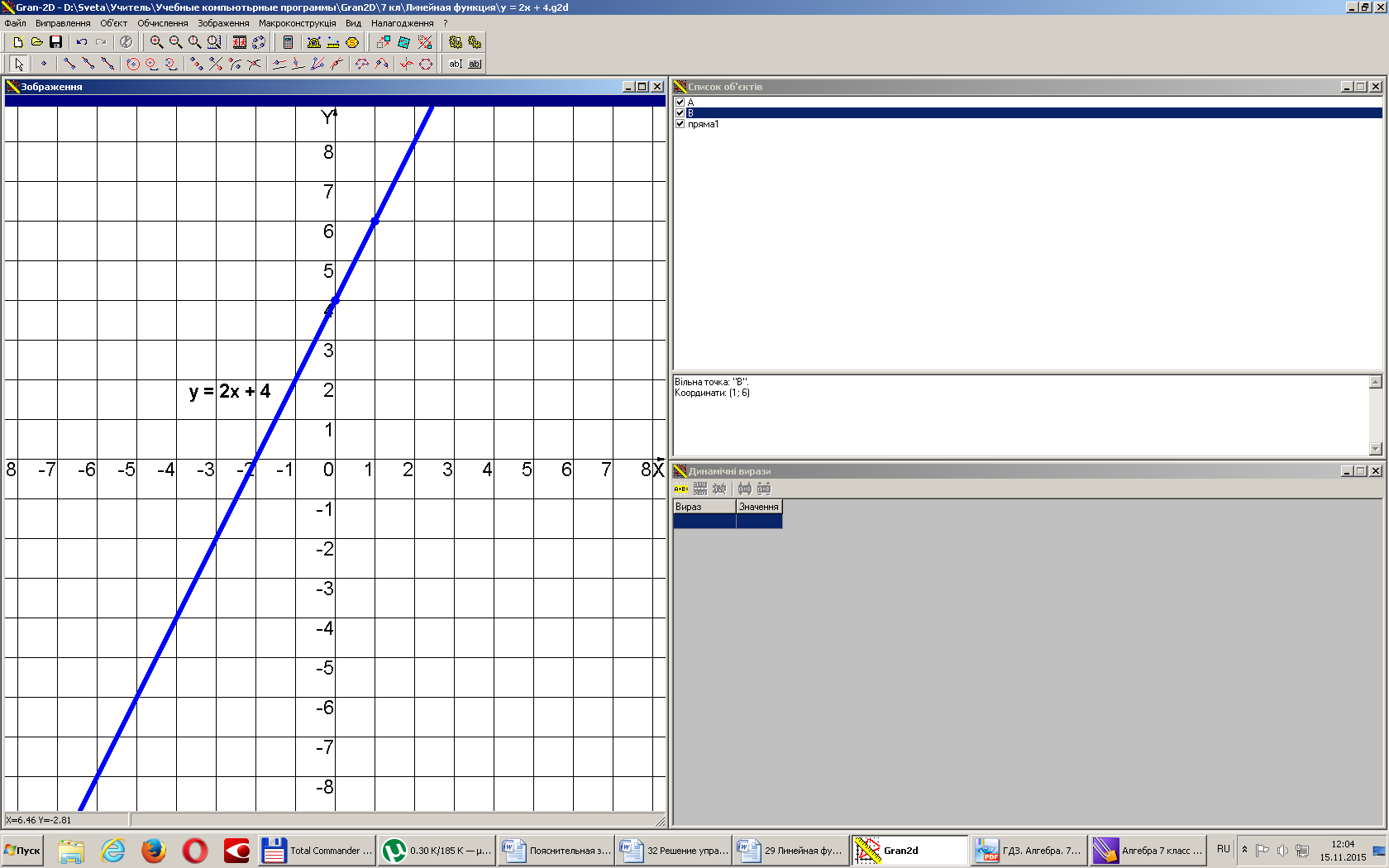
а) (лин. функ.,гр.-прямая).х

0

1

у

4

6

б) х = -1,5, то у = 1.

3. В одной и той же системе координат постройте графики функций:

а) ; б) .

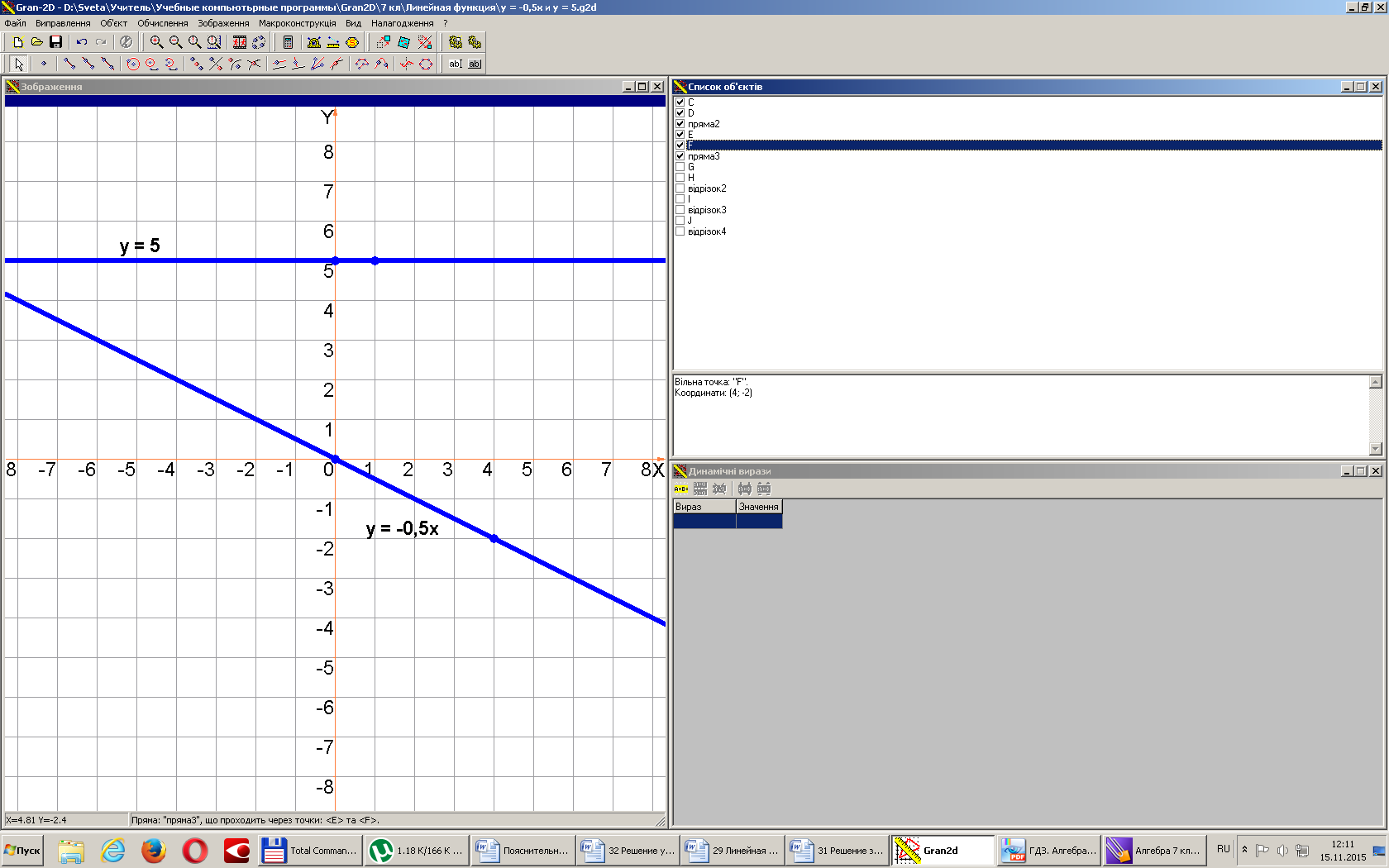
1) у = -0,5х (прям. пропор.,гр.-прямая, проходящ. через начало координат),

х

0

4

у

0

-2

2) у = 5 (лин. функ.,гр.-прямая, проходящая через точку (0; 5) и параллельная оси х).

4. Найдите координаты точки пересечения графиков функций и .

Решение.

Т.к. графики функций пересекаются, то координаты точки пересечения удовлетворяют каждому из уравнений (т.е. абсциссы и ординаты в этой точке равны).

Левые части наших уравнений равны, то и правые равны. Приравниваем.

,

,

.

.

(1; 18) - координаты точки пересечения графиков. Ответ: (1; 18).

5. Задайте формулой линейную функцию, график которой параллелен прямой и проходит через начало координат.

Решение.

График параллелен прямой , значит, угловые коэффициенты равны. Т.к. прямая проходит через начало координат, то это прямая пропорциональность. Значит, .

6*. При каком значении b график функции у = -5х + b проходит через точку В(4; -24)?

Т.к. график проходит через точку В(4; -24), то ее координаты удовлетворяют уравнению прямой.

-5 ∙ 4 + b = -24, -20+ b = -24, b = -4.

Ответ: -4.

6. Подведение итогов урока.

7. Домашнее задание. п. 12-16 (повторить теорию). Задание в тетради.

Домашняя контрольная работа № 3 по теме «Функции».

1. Функция задана формулой .Определите:

а) значение у, если х = -3,5;

б) значение х, при котором у = -5;

в) проходит ли график функции через точку К(10; -5).

Решение.

а) х = -3,5, то ;

б) у = -5, то ,

, .

в) К(10; -5), то ,

. Значит К(10; -5) не принадлежит графику.

2. а) Постройте график функции ;

б) Укажите с помощью графика, чему равно значение х при у = -6.

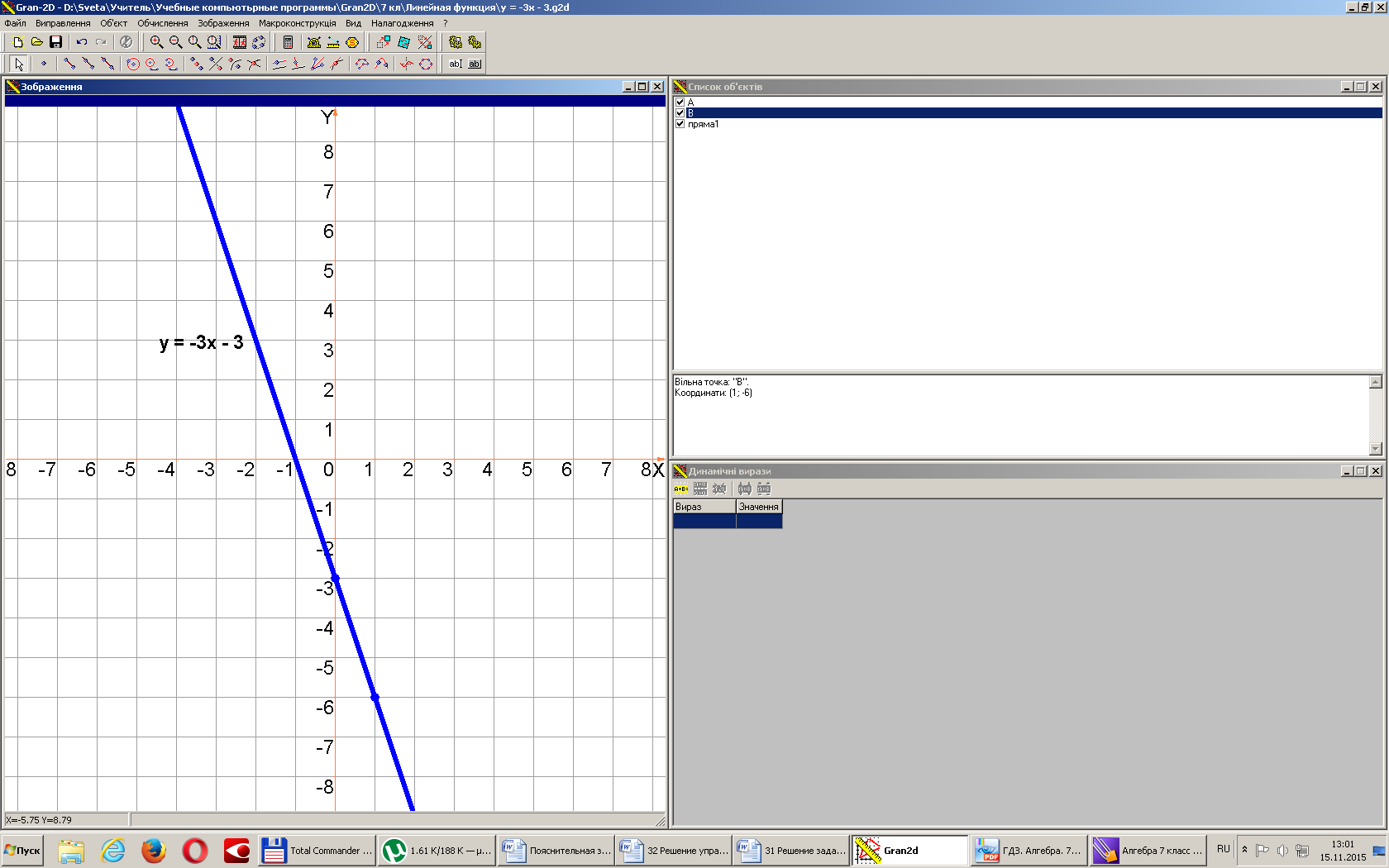
а) (лин. функ.,гр.-прямая).х

0

1

у

-3

-6

б) у = -6, то х = 1.

3. В одной и той же системе координат постройте графики функций:

а) ; б) .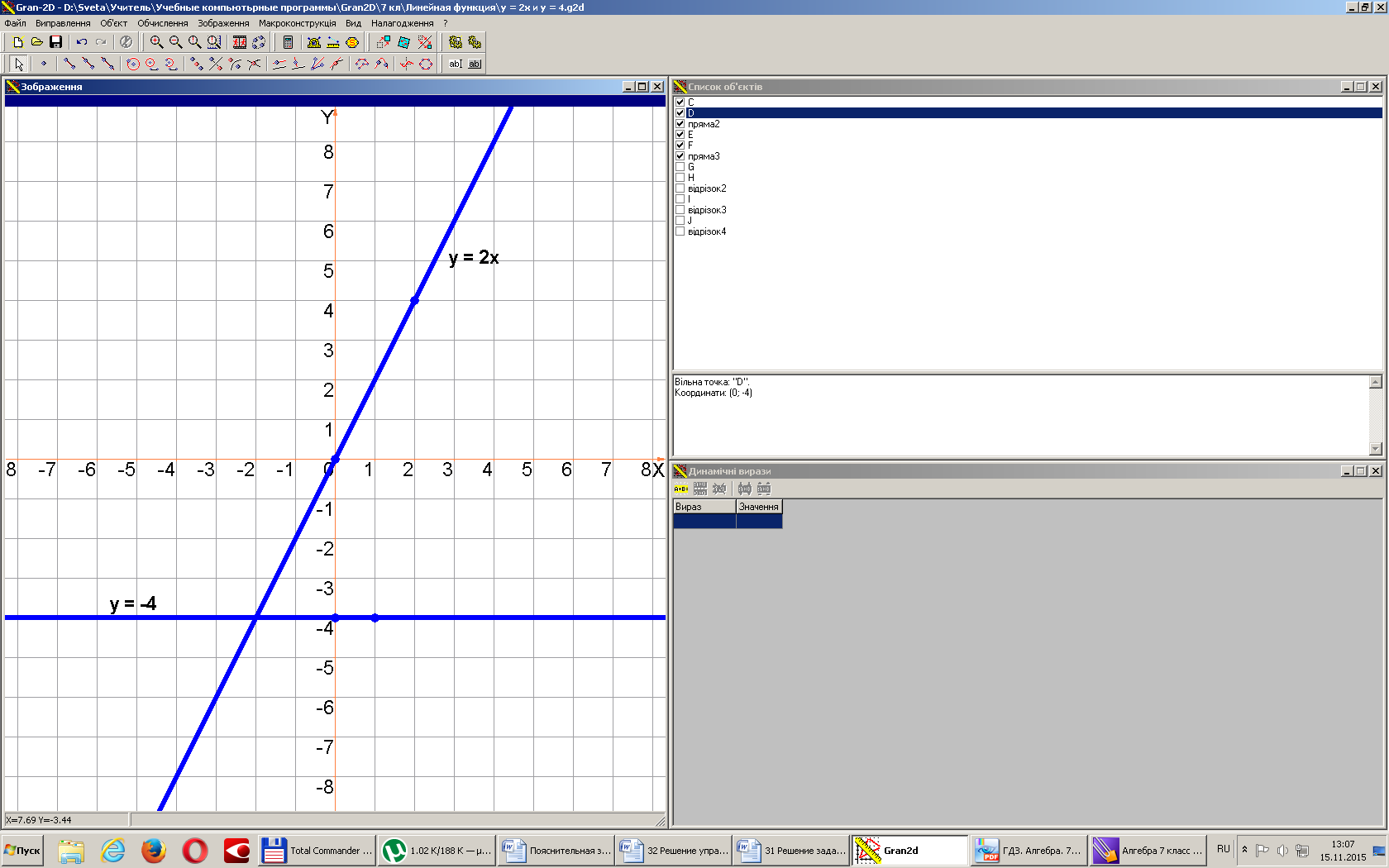

1) у = 2х (прям. пропор.,гр.-прямая, проходящ. через начало координат),

х

0

2

у

0

4

2) у = -4 (лин. функ.,гр.-прямая, проходящая через точку (0; -4) и параллельная оси х).

4. Найдите координаты точки пересечения графиков функций и .

Решение.

Т.к. графики функций пересекаются, то координаты точки пересечения удовлетворяют каждому из уравнений (т.е. абсциссы и ординаты в этой точке равны).

Левые части наших уравнений равны, то и правые равны. Приравниваем.

,

,

.

.

(2; -29) - координаты точки пересечения графиков. Ответ: (2; -29).

5. Задайте формулой линейную функцию, график которой параллелен прямой и проходит через начало координат.

Решение.

График параллелен прямой , значит, угловые коэффициенты равны. Т.к. прямая проходит через начало координат, то это прямая пропорциональность. Значит, .

7 класс

УРОК № 32. Глава 2. Функции (11 часов)

Тема. Решение упражнений по теме «Функции».

1. Функция задана формулой .Определите:

а) значение у, если х = 0,4;

б) значение х, при котором у = 3;

в) проходит ли график функции через точку С(-6; -12).

2. а) Постройте график функции ;

б) Укажите с помощью графика, чему равно значение у при х = -1,5.

3. В одной и той же системе координат постройте графики функций:

а) ; б) .

4. Найдите координаты точки пересечения графиков функций и .

5. Задайте формулой линейную функцию, график которой параллелен прямой и проходит через начало координат.

6*. При каком значении b график функции у = -5х + b проходит через точку В(4; -24)?

Домашняя контрольная работа № 3 по теме «Функции».

1. Функция задана формулой .Определите:

а) значение у, если х = -3,5;

б) значение х, при котором у = -5;

в) проходит ли график функции через точку К(10; -5).

2. а) Постройте график функции ;

б) Укажите с помощью графика, чему равно значение х при у = -6.

3. В одной и той же системе координат постройте графики функций:

а) ; б) .

4. Найдите координаты точки пересечения графиков функций и .

5. Задайте формулой линейную функцию, график которой параллелен прямой и проходит через начало координат.