- Учителю
- Конспект урока по алгебре в 9 классе по теме: «Формулы суммы n первых членов геометрической прогрессии».
Конспект урока по алгебре в 9 классе по теме: «Формулы суммы n первых членов геометрической прогрессии».
Конспект урока по алгебре в 9 классе по теме:
«Формулы суммы n первых членов
геометрической прогрессии».
Бархатова О.А.
учитель математики
МОУ СОШ №16
г.Усолье-Сибирское
Цели и задачи:
образовательные - познакомить учащихся с выводом формулы сумм n первых членов геометрической прогрессий; учить учащихся применять полученные формулы при решении задач.
развивающие - развивать творческую и мыслительную деятельность учащихся на уроке посредством анализа и сравнения арифметической и геометрической прогрессий, вывода формулы; с помощью решения задач исследовательского характера и самостоятельного вывода учащимися формулы развивать интеллектуальные качества личности школьников такие, как самостоятельность, гибкость, способность к оценочным действиям, обобщению, быстрому переключению; способствовать формированию навыков коллективной и самостоятельной работы; в целях развития эмоций учащихся обеспечить в ходе урока ситуации эмоциональных переживаний; формировать умения чётко и ясно излагать свои мысли.
воспитательные - прививать учащимся интерес к предмету посредствам решения исторических задач; формировать умения аккуратно и грамотно выполнять математические записи, составлять таблицы.
Ход урока.
Сегодня у нас в классе состоится совет - Совет мудрецов.
Мудрецы - ученики, сидящие в классе .
Учитель: Тема урока: «Формулы суммы n первых членов геометрической прогрессии». Вдумайтесь в формулировку темы, сформулируйте и назовите проблемы, которые на ваш взгляд мы должны решить по этой теме.
Учащиеся называют проблемы, а учитель кратко записывает их на доске и обещает, что на все вопросы мы постараемся узнать ответы на этом или последующих уроках. Учитель сообщает учащимся, какие ещё проблемы ему удалось выделить.
Проблемы:
-
Зачем нужно уметь вычислять сумму n первых членов геометрической прогрессии?
-
Как выглядит формула суммы n первых членов геометрической прогрессии?
-
Как вывести формулу суммы n первых членов геометрической прогрессии?
-
В чём сходства и различия в выводе формул суммы n первых членов арифметической и геометрической прогрессии?
-
Актуализация знаний.
1. Работа по карточкам( двое учащихся у доски), (двое на месте решают), (двое разгадывают кроссворд).
Учитель просит учащихся выполнить задания, решения которых поможет повторить ранее изученный материал и лучше усвоить новый. Ответы на поставленные вопросы выясняются в ходе беседы.
Задания классу:
-
Прослушаем историю о строительстве стены на даче нового русского
Новый русский решил отгородить бассейн на даче фигурной стеной. Позвав строителей,
начал объяснять.
-
В нижний ряд укладывается 19 блоков, на него кладётся 17 блоков, затем 15 и так далее. Всего 8 рядов.
5
7
11
17
9
13
15
19
Выпишем числа, соответствующие количеству блоков каждого ряда:
19, 17, 15, 13, 11, 9, 7, 5 (учитель записывает числа на доске). Получили последовательность чисел. Опишите её.
Ответ: Эта последовательность является примером конечной убывающей арифметической прогрессии, первый член которой а1= 19, а разность d = 2. Любой член этой прогрессии можно вычислить по формуле: аn = 2n + 21, где n натуральные числа от 1 до 8.
-
Сформулируйте определение арифметической прогрессии.
-
Рассмотрим бесконечно убывающую арифметическую прогрессию, первый член которой а1 = 19, а разность d = 2. Какие задания вы могли бы предложить классу, используя эти данные так, чтобы они могли бы выполнить их устно? Решите составленные задачи.
Варианты заданий:
-
Найдите 18-й член прогрессии.
-
Является ли число 1 (21; 8) членом последовательности?
-
Сколько положительных чисел являются членами этой прогрессии?
-
Чему равен первый отрицательный член этой прогрессии? и т. д.
Как быстрее вычислит
количество блоков в фигурной стене? По какой формуле можно найти количество блоков?
-
Опишите данные последовательности:
( последовательности чисел заранее записаны на доске):
а) 1; 2; 3;4; 5; 6; … ,
б) 5; 5; 5; 5; 5; … ,
в) 0; 0; 0; 0; 0;…
г) 1; 2; 22; 23; 24; 25;… 263;…
-
Рассмотрим последнюю последовательность: 1; 2; 22; 23; 24; 25;… 26;… Опишите её.
Ответ: Эта последовательность является примером бесконечной возрастающей геометрической прогрессии, первый член которой b1=1, а знаменатель q = 2. Любой член этой прогрессии можно вычислить по формуле: bn=2n-1, где n![]() N.
N.
Проверка решений по карточкам. Оценивание. .
-
Поиск новых знаний.
В виде игровой ситуации учащимся предлагается задача, которая содержит жизненные факты, но при решении которой возникает необходимость в выводе новой формулы.
ЗАДАЧА
Однажды незнакомец постучал в окно к богатому купцу и предложил сделку «Я буду ежедневно в течение 30 дней приносить тебе по 100 000 р. А ты мне в первый день за
100 000р. Дашь 1к., во второй день за 100 000р.-2к.и так каждый день будешь увеличивать предыдущее число денег в два раза. Если тебе выгодна сделка, то с завтрашнего дня начнём».
Купец обрадовался такой удаче. Он подсчитал, что за 30 дней он получит от незнакомца 3 000 000р. На следующий день они пошли к нотариусу и узаконили сделку.
Кто в этой сделке проиграл: купец или незнакомец? Учащиеся составляют последовательность чисел: 1;2;4;8;16;….Убеждаются , что эти числа составляют геометрическую прогрессию. Обращаются с вопросом: «Можно ли подсчитать по формуле сумму первых членов геометрической прогрессии?» Я даю утвердительный ответ при этом усиливаю проблемность, рассказывая легенду о шахматах.
Легенда о шахматной доске
Шахматы - одна из самых древних игр. Она существует уже многие века и неудивительно, что с нею связаны различные придания, правдивость которых, за давностью времени, невозможно проверить.
Чтобы понять ее, не нужно вовсе уметь играть в шахматы: достаточно точно знать, что игра происходит на доске, разделенной на 64 клетки (попеременно черные и белые).
Шахматная игра была придумана в Индии, и когда индусский царь Шерам познакомился с нею, он был восхищен ее остроумием и разнообразием возможных в ней положений.
Узнав, что она изобретена одним из его подданных, царь приказал его позвать, чтобы лично наградить за удачную выдумку.
Изобретатель, его звали Сета, явился к трону повелителя. Это был скромно одетый ученый, получавший средства к жизни от своих учеников.
- Я желаю достойно вознаградить тебя, Сета, за прекрасную игру, которую ты придумал, - сказал царь. Я достаточно богат, чтобы исполнить самое смелое твое пожелание - предложил царь.
- Назови награду, которая тебя удовлетворит, и ты получишь ее.
Сета молчал.
- Не робей, - ободрил его царь. - Выскажи свое пожелание. Я не пожалею ничего, чтобы исполнить его.
На что Сета сказал, что он обдумает ответ и завтра сообщит царю свою просьбу.
На другой день, когда Сета сообщил свою просьбу, царь удивился беспримерной скромности бедного Мудреца.
- Повелитель, - сказал Сета, - прикажи выдать мне за первую клетку шахматной доски одно пшеничное зерно.
- Простое пшеничное зерно? - изумился царь.
- Да, повелитель. За вторую клетку выдать 2 зерна, за третью - 4, за четвертую - 8, за пятую - 16, за шестую - 32…
- Довольно, - с раздражением прервал его царь. Ты получишь свои зерна за все 64 клетки доски, согласно твоему желанию. Но знай, что твоя просьба недостойна моей щедрости. Поистине, как учитель, ты мог бы показать лучший пример уважения к доброте своего государя. Слуги мои вынесут тебе твой мешок с пшеницей.
Царь смеялся.
Учитель: О, Мудрецы 9 класса, посоветуйтесь и скажите, стоит ли царю смеяться?
(запись на доске 1, 2,8, 16, 32, . . . S64 - ?)
Решение:
S = 1+ 2+22+ 23+ 24+ 25+… +263
2 S = 2+22+ 23+ 24+ 25+26… +264
2 S S = (2 + 22 + 23 + 24 + 25 + 26 +… + 264) ( 1 + 2 + 22 + 23 + 24 + 25 +… +263)S = 264 1=18446744073709551615
Учитель: Как велико это число?
Это «чудовищное» число звучит так: 18 квинтиллионов 446 квадриллионов 744 триллиона 73 миллиарда 709 миллионов 551 тысяча 615.
И все-таки, история о шахматах могла закончиться иначе.
Индусский царь не в состоянии был выдать подобной награды. Но он мог бы легко, будь он силен в математике, освободиться от столь обременительного долга. Для этого нужно было лишь предложить изобретателю самому отсчитать себе зерно за зерном всю причитавшуюся ему пшеницу.
Чтобы отсчитать миллион зерен, понадобилось бы не менее 10 суток неустанного счета. Чтобы отсчитать себе все зерно изобретателю потребовалось бы примерно
586 549 402 017 лет.
Проанализировав решение предыдущей задачи, выведите формулу суммы n первых членов геометрической прогрессии, если первый член этой прогрессии b1, n-й член прогрессии bn , Sn- сумма первых n членов, пользуясь учебником.(работаем в парах)
Учитель: Итак, мы получили формулу суммы n первых членов геометрической прогрессии: Sn=![]() при q
при q![]() 1 и Sn= nb1 при q = 1
1 и Sn= nb1 при q = 1
Вернёмся к задаче о купце и незнакомце. Подсчитайте по формуле и ответьте на вопрос «Кто проиграл в сделке?»
-
Оценивание учащихся.
-
Рефлексия. Подведение итогов.
Учащиеся дают ответ на вопрос: В чём сходства и различия в выводе формул суммы n первых членов арифметической и геометрической прогрессии?
Учитель просит учащихся оценить, как они справились с работой на уроке, что было удачным, а что нет; на все ли поставленные в начале урока вопросы были найдены ответы, а какие ещё предстоит решить.
V. Информация о домашнем задании.
Используя таблицу, сравнить арифметическую и геометрическую прогрессии
Основания для сравнения
Существенные признаки сходства или различия
Арифметическая прогрессия
Геометрическая прогрессия
С Х О Д С Т В А
1.
2.
3.
и т. д.
-
-
-
Р А З Л И Ч И Я
1.
2.
3.
и т. д.
-
-
-
-
-
-Результат сравнения оформить в виде таблицы.
О мудрецы времен!
Дружней вас не сыскать.
Совет сегодня завершен,
Но каждый должен знать:
Познание, упорство, труд
К прогрессу в жизни приведут.
Учитель: У каждого из вас на столе карточки (розовая, жёлтая). Уходя из класса, прикрепите на доску одну из них.
Карточка розового цвета обозначает: "Я удовлетворён уроком, урок был полезен для меня, я много, с пользой и хорошо работал на уроке, и получил заслуженную оценку, я понимал всё, о чём говорилось и что делалось на уроке".
Карточка желтого цвета обозначает: "Пользы от урока я получил мало, я не очень понимал, о чём идёт речь, мне это не очень нужно,
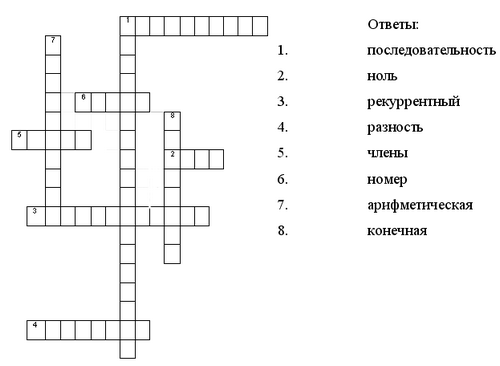
По горизонтали
1. Первый из двух стоящих рядом членов последовательности
2. Разность последовательно одинаковых членов
3. Способ задания последовательности
4. Число в арифметической прогрессии
5. Элементы, из которых состоит последовательность
6. Натуральное число, обозначающее место члена в последовательности
По вертикали
1. Функция, заданная на множестве натуральных чисел
7. Вид последовательности
8. Последовательность, содержащая конечное число членов.
8