Урок по алгебре и началам анализа 10 класс.

Тема: "Показательная функция, уравнения, неравенства"

УМК Алимов Ш.А

Бузина Галина Владимировна - учитель математики МКОУ «СОШ №13» с. Надежда Ставропольского края

Цель урока: обобщить и закрепить теоретические знания, методов решения показательных уравнений и неравенств на основе свойств показательной функции.

Оборудование:

• Компьютеры

• Презентация слайдов по теме

• Карточки

Структура урока:

(с точки зрения применения методов обучения)

1. Организационный момент.

2. Постановка цели урока.

3. Работа консультантов

1. Слайд: тема "Показательная функция , при , при ее графики и свойства". Актуализация опорных знаний. Блиц - опрос.

2. Слайд: анализ методов решения показательных уравнений. Диагностика уровня формирования практических навыков. Выбор и решение уравнений указанным методом.

3. Слайд: Решение показательных неравенств. Математический диктант.

4. Выполнение практической работы: Дальше, дальше.

5. Применение показательной функции в природе и технике.

6. Подведение итогов.

7. Домашнее задание.

1.Организационный момент. Через 1,5 года вы подойдете к важной черте вашей жизни к итоговой аттестации. С какими заданиями вы уже можете справиться. Что вы изучали на последних уроках. Сегодняшний урок -урок обобщения .По какой теме? Открыли тетради записали число ,классная работа. Сегодняшний урок я для себя назвала урок 20 задач, я надеюсь ,что все вместе вы сможете решить более20 задач. В классе работают консультанты:

Сейчас вы работаете с 1 консультантом по теме показательная функция

Слайд: тема "Показательная функция , при , при ее графики и свойства".

Актуализация опорных знаний. Блиц - опрос.

1. Какая функция называется показательной?

2. Какова область определения функции y=0,3^x?

3. Каково множество значения функции y=3^x?

4. Дайте определение возрастающей, убывающей функции.

5. При каком условии показательная функция является возрастающей?

6. При каком условии показательная функция является убывающей?

7. Возрастает или убывает показательная функция

8. Определить при каком значении a функция 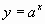проходит через точку А(1; 2);

9.график

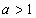
Сейчас вы работаете с 2 консультантом по теме показательные уравнения

Слайд: анализ методов решения показательных уравнений. Диагностика уровня формирования практических навыков. Выбор уравнений указанным методом.

Диагностика уровня формирования практических навыков.

Указать способы решения показательных уравнений.

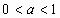
Результаты занесите в таблицу: Если все верно 1балл, если 1 ошибка-0.5 балла

Сейчас вы работаете с 3 консультантом по теме показательные неравенства

3. Слайд: Решение показательных неравенств. Математический диктант. Если ответ правильный то «+»; если неверный то «-» Если все верно 1балл, если 1 ошибка-0.5 балла

Функция - возрастающая

Функция - возрастающая

Решением неравенства - является X<5

Решением неравенства - является X<3

Решением неравенства - является

.Выполнение практической работы: Дальше, дальше

Практическая работа

1 уровень

1

(0,5 балл)

6

().5 балл)

2

(1 балл)

7

4^(х+1)> 16 (0,5 балл)

3

(1 балл)

8

(1 балл)

4

(1 балл)

9

. (1 балл)

5

3^2х-1 + 3^2х = 108 (1 балл)

10

. (1 балл)

2 уровень

11

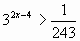(2 балл)

14

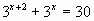(2 балл)

12

Найдите значение выражения 12,8xо +17, если xо - наименьший корень уравнения (2 балл)

15

(2 балл)

13

(2 балл)

3 уровень

16

Решите уравнение. В ответе укажите число его корней.

(3 балл)

18

Найдите область определения функции

(3 балл)

17

(3 балл)

19

(3 балл)

20

>16 (3 балл)

В это время консультанты работают у доски, решая выбранные ими задания 3 уровня.

ОТВЕТЫ

Практическая работа

1 уровень

1

-3

6

2

1

7

3

2

8

4

0

9

5

2

10

2 уровень

11

14

12

17

15

13

-81

3 уровень

16

3

18

17

3; -1

19

20

Закончили. .Посчитайте баллы, которые вы набрали. Оцените себя.

Консультанты объясняют как они решали задания 3 уровня.

Где применяется показательная функция? С этим нас познакомит 4 консультант.

Слайд «Применение показательной функции»

Понятие функции было ведено в 17 веке. Сейчас ваши знания находятся на уровне ученых того времени. Но сейчас 21 век. У вас есть большая перспектива развития. Учитесь и дерзайте.