- Учителю
- Разработка заключительного урока по теме 'Производная' (11 класс)
Разработка заключительного урока по теме 'Производная' (11 класс)
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
СРЕДНЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«ИСОВСКИЙ ГЕОЛОГОРАЗВЕДОЧНЫЙ ТЕХНИКУМ»
Методическая разработка
открытого урока по математике
« Производная и ее приложения»
для студентов специальности
0601 « Экономика и бухгалтерский учет (по отраслям)»
Автор: С.А.Иванова - преподаватель математики, информатики и вычислительной техники ИГРТ, высшей категории.
Нижняя Тура
2006
Открытый урок по математике
« Производная и ее приложения»
в группе БГР - I - 1 (03)
Дата 21 апреля 2006 год.
Преподаватель: Иванова Светлана Александровна.
Тип урока: систематизации и обобщения изученного материала.
Форма организации познавательной деятельности студентов: коллективная.
Цели урока:
-
обобщение и систематизация теоретических знаний по темам: «Производная функции», «Свойства функции», «Приложения производной»;
-
показать студентам практическое применение темы в повседневной жизни;
-
показать студентам межпредметные и внутрипредметные связи;
-
развитие у студентов логического мышления;
-
продолжить работу по закреплению у студентов навыков работы со справочной литературой;
-
развитие навыков коллективной работы;
-
воспитание товарищества и взаимовыручки.
Ход урока:
-
Организационный момент - 2 мин.
-
Подготовка учащихся к активному усвоению знаний - 3 мин.
-
Обобщение и систематизация изученного (в игровой форме) - 80 мин.
а) Визитка (название команды, девиз, эмблема) - 5 мин.
б) Конкурс библиографов - 20 мин.
в) Конкурс теоретиков - 5 мин.
г) « Найди пару» - 10 мин.
д) Конкурс « переводчиков» - 10 мин.
е) « Графопостроители» - 15 мин.
ж) Конкурс практиков - 15 мин.
з) « Смекалка» - 10 мин.
и) Конкурс кроссвордов - 10 мин.
-
Итог урока - 5 мин.
Литература:
1) Л.Э.Генденштейн и др. « Наглядный справочник по алгебре и началам анализа с примерами для 7-11 классов».
М.: « Илекса», 2001г.
2) Л.В.Горбачева. « Нестандартный урок по математике. Методические разработки. Часть II.»
Челябинск, 1994г.
3) Л.О.Денищева и др. « Учебно-тренировочные материалы для подготовки к единому государственному экзамену».
4) В.Г.Коваленко. « Дидактические игры на уроках математики».
М.: « Просвещение», 1990г.
5) Р.Д.Лукин и др. « Устные упражнения по алгебре и началам анализа. Книга для учителя».
М.: « Просвещение», 1989г.
6) Л.Н.Толстой. Полное собрание сочинений. Том 10.
М.: Государственное издательство художественной литературы, 1963г.
Конспект урока
Группа заранее разделилась на 3 части: 2 команды и болельщики. Команды сидят за отдельными столами, а болельщики сидят в конце кабинета за столами.
1 этап урока.
Преподаватель: Здравствуйте, присаживайтесь! Сегодня у нас с вами заключительный урок по теме «Производная». Мы должны обобщить теоретические знания по теме и показать практическое применение этих знаний в повседневной жизни.
2 этап урока.
Преподаватель: На предыдущих уроках мы с вами познакомились с определением производной, правилами дифференцирования, признаками возрастания и убывания функции, применением производной к построению графиков функций. Но проводить урок мы будем в игровой форме.
3 этап урока.
Преподаватель: Вам было предложено разделиться на две команды. Все на уроке получат оценки: и участники команд, и болельщики. Сейчас познакомимся с нашими командами.
Проходит конкурс «Визитка» (название команды, девиз, эмблема). Жюри в таблице итогов подсчитывают баллы (Приложение 1). Итоги объявляются жюри, по возможности, сразу после конкурса.
Преподаватель: С командами мы познакомились, а теперь, капитаны команды, для конкурса «Библиографов», необходимо от каждой команды по 1 человеку. Задача ваша состоит в том, чтобы в словарях (каждой команде предоставляются одинаковые словари) найти как можно больше понятий, относящихся к нашей теме. Записать их определения и выделить из них главные (Приложение 2).
Преподаватель: Проверим, как команды подкованы теоретически. Я буду задавать вопросы поочередно (по часовой стрелке). Вам необходимо за 3 мин. дать как можно больше правильных ответов. Конкурс «Теоретики» проходит в виде игры «Слабое звено». (Приложение 3)
Подводятся итоги 2 конкурсов («Визитка», «Теоретики»).
Преподаватель: Переходим к следующему конкурсу «Найди пару». В предложенных вам таблицах необходимо функции в каждой ячейке найти пару из предложенных в ячейках этой же таблицы. Если такого ответа не найдено в ячейках таблицы, то запишите правильный ответ.
Командам выдается вариант А, а болельщикам А и Б. (Приложение 4).
Преподаватель: Мы переходим к конкурсу «Переводчики». Вам необходимо выполнить задания, предложенные на карточках (Приложение 5).
Командам выдается вариант 1, а болельщикам 1 и 2.
Преподаватель: Пожалуйста, «библиографы» сдайте свои работы жюри и присоединяйтесь к своей команде.
По возможности, подводятся итоги конкурсов.
Преподаватель: Мы продолжаем нашу игру. Сейчас у нас состоится конкурс «Графопостороители». Командам необходимо провести исследование функции у=2*х4-8*х с помощью производной и построить ее график.
Болельщикам предлагается по вариантам: I вариант - у=3*х-х3;
II вариант - у=х3-3*х.
Преподаватель: Следующий наш конкурс под названием « Практики». Задание звучит как для команд, так и для болельщиков. Слушаем внимательно.
У Л.Н.Толстого есть рассказ « Много ли человеку земли надо». В нем речь идет о крестьянине Пахоме, который мечтал о собственной земле. Вот, наконец, собрал Пахом необходимую сумму и предстал перед требованием старшины. Старшина ему ответил: « Сколько за день земли обойдешь, вся твоя будет за 1000 руб. Но, если к заходу солнца не возвратишься на место, с которого вышел, пропали твои деньги». Выбежал утром Пахом, прибежал на место и упал без чувств, обежав прямоугольник, периметром 40 км. Наибольшую ли площадь земли получил Пахом?
Ваша задача решить сейчас: Каким должен быть прямоугольник, чтобы, пробежав по его периметру, Пахом получил наибольший по площади участок земли. Вспомните решение задач на max - min.
Пока команды и болельщики решают задачу, жюри подводит итоги предыдущих конкурсов.
Преподаватель: Подходит к концу наше занятие. У нас осталось два конкурса. Итак, конкурс « Смекалка».
Задание командам и болельщикам:
1. Найти производную функции: y=sin![]() *x2-cos
*x2-cos![]() *x (2*x).
*x (2*x).
2. Найти производную функции: y=2*tgx*ctgx*x2-![]() +sin
+sin![]() , где х
, где х![]() , n
, n![]() Z. (4*х-х2).
Z. (4*х-х2).
3. Почему функция y=x3+x+2 не имеет экстремумов? (y1=3*x2+1>0 ![]() x
x![]() R).
R).
Преподаватель: Домашним заданием командам было приготовить кроссворд по нашей теме. Команды обмениваются кроссвордами. И отгадывают кроссворд, приготовленный соперниками. А болельщики работают со мной.
С болельщиками идет игра на отгадывание ребусов, приготовленных ранее ребятами из группы к зачету. Ребусы только по теме «Производная».
Преподаватель: Вот, и подошло к концу наше занятие. Все, я думаю, хорошо усвоили эту тему. Работу команд через несколько минут оценит жюри, а у болельщиков я соберу их работы, проверю и результаты скажу на следующем занятии. Пока жюри подводит итоги игры, мы с вами еще поотгадываем ребусы, шарады, метаграммы (для примера Приложение 6).
Объявляются итоги игры, члены жюри высказывают свое мнение. Преподаватель благодарит за урок всех и награждает участников сладкими призами.
Приложение 1
Таблица итогов игры
Конкурс
« Максики»
«Стационарики»
1.Визитка
а) Название (1б)
б) Девиз (1б)
в) Эмблема (1б)
2. Библиографы (0,5б за каждое правильное понятие).
3. «Теоретики» (1б за каждый правильный ответ за 3 мин.)
4. «Найди пару» (0,5б за каждый правильный ответ)
5. «Переводчики»(5б за правильно выполненную карточку: 1з.-2б; 2з.-1б; 3з. - 2б).
6. «Графопостроители»( 3б за правильное исследование и построение графика функции)
7. «Практики» (3б за правильно решенную задачу)
8. Конкурс «Смекалистых» (2б за каждое верно выполненное задание)
9. Конкурс кроссвордов (2б за сам кроссворд + по 0,5 балла за каждый правильный ответ на вопрос кроссворда + 1б за корректную постановку вопросов в кроссворде)
ИТОГ ИГРЫ:
Приложение 2
По алфавитному указателю словарей найти и записать понятия, которые можно отнести к теме нашей игры. Выделить из них основные, записать их определения.
Предлагаются:
1) Учебник А.А.Дадаян «Математика»
2) «Энциклопедический словарь юного математика».
Этот материал только у жюри.
В них можно найти следующие понятия:
алгебра с.13-17(1)
асимптота с. 31(1)
возрастание и убывание функции с. 41(1)
геометрические задачи на экстремум с. 55-57(1)
график с. 80-83(1)
дифференцирование с. 100(1)
касательная с. 132-133(1)
максимум с. 55(1)
математика с. 172-178(1)
метод интервалов с. 215(1)
минимум с. 55(1)
непрерывная функция с. 209-211(1)
область определения функции с. 318(1)
область значения функции с. 318(1)
основные правила дифференцирования с. 342(1)
предел с. 245-248(1)
симметрия с. 61(1)
функция с. 315-322(1)
экстремумы функции с. 334-335(1)
элементарные функции с. 335-336(1)
мгновенная скорость изменения функции гл.V(2)
угловой коэффициент касательной к линии в данной точке гл. IX(2)
Приложение 3
Вопросы команде 1.
-
Отношение между элементами двух множеств, при котором каждому элементу первого множества соответствует один элемент второго множества, называется (функцией).
-
Производная константы равна (нулю).
-
Производная суммы двух непрерывных функций равна (сумме производных слагаемых).
-
Экстремумами функции называются точки (максимума и минимума).
-
Множество всех точек координатной плоскости, удовлетворяющих уравнению y=f(x), называется (графиком функции y=f(x)).
-
Производная функции (sin(k*x))1 равна (k*cos(k*x)).
-
Если при переходе через стационарную точку производная меняет свой знак с минуса на плюс, то эта точка (минимума).
-
Нули функции - это те значения х из области определения функции, для которых выполняется равенство (f(x)=0).
-
Если для любых двух значений из области определения функции большему значению аргумента соответствует меньшее значение функции, то функция называется (убывающей).
-
Если функция четная, то ее график (симметричен относительно оси Оу).
-
Функция вида y=f(x) называется нечетной, если (область определения симметрична относительно нуля и выполняется равенство f(-x)= -f(x) ).
-
Производная функции (k*x+b)1 равна (k).
-
Физический смысл производной (мгновенная скорость).
-
Производная функции (5*х4)1 равна (20*х3).
-
Производная функции (х-6)1 равна (-6*х-7).
-
Производная функции (
 )1 равна (
)1 равна ( ).
). -
Производная функции (
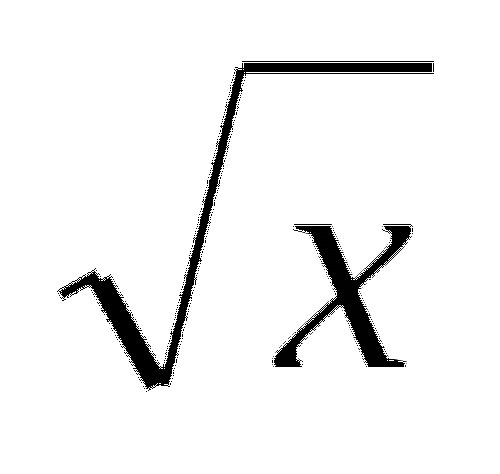 )1 равна ( -
)1 равна ( - 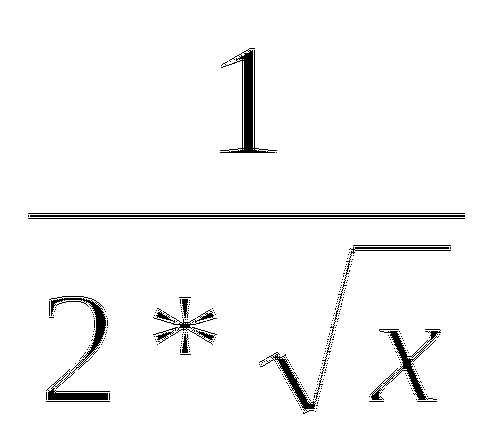 ).
). -
Если функция отрицательна, то график ее расположен (ниже оси Ох).
-
Назовите область определения функции у=
 (х
(х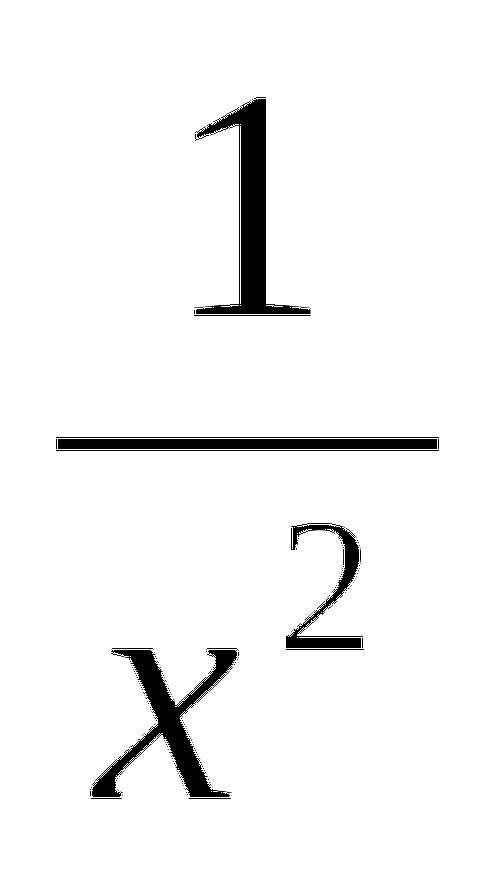 - 2).
- 2). -
Если область определения функции х
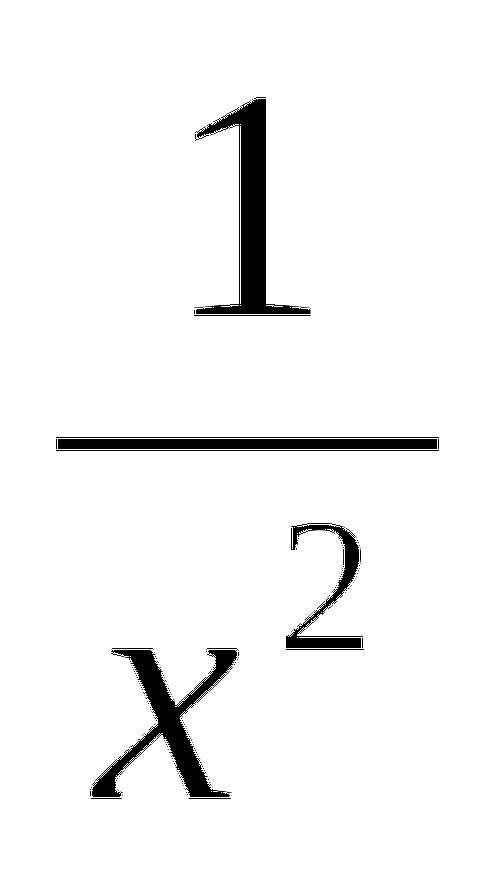 1, то х=1 - это (вертикальная асимптота графика функции).
1, то х=1 - это (вертикальная асимптота графика функции). -
Производная функции (2*x-3)1 равна (2).
-
Производная функции (
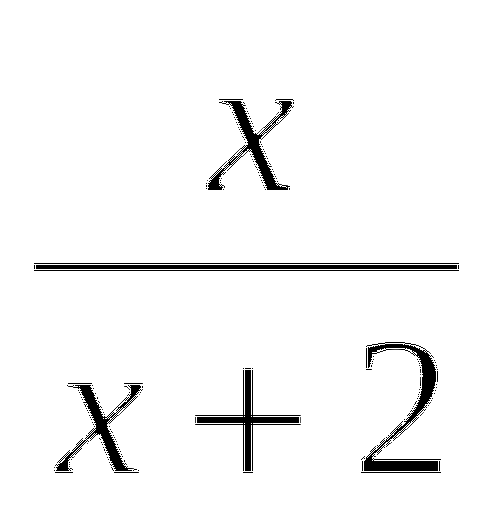 -а)1 равна (0).
-а)1 равна (0). -
Производная функции (u*v)1 равна (u1 *v+u *v1).
Вопросы команде 2.
-
Если для любых двух значений из области определения функции большему значению аргумента соответствует большее значение функции, то функция называется (возрастающей).
-
Производная функции (х)1 равна (1).
-
Производная степенной функции (хр)1 равна (р*хр-1).
-
Стационарные точки функции - это те значения аргумента, для которых выполняется равенство ( у1=0).
-
Нахождение производной функции называется (дифференцированием).
-
Предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю, называется (производной функции).
-
Производная функции (cos(k*x+b))1 равна (-k*sin(k*x+b)).
-
На графике нули функции - это (точки пересечения графика функции с осью Ох).
-
Если производная функции при переходе через стационарную точку меняет свой знак с плюса на минус, то эта точка (максимума).
-
Функция y=f(x) называется четной, если (область определения функции симметрична относительно нуля и выполняется равенство f(-x)=f(x)).
-
Если функция нечетная, то ее график (симметричен относительно начала координат).
-
Производная функции (х4)1 равна (4*х3).
-
Геометрический смысл производной - это (угловой коэффициент касательной, проведенной в данной точке к данной функции).
-
О четности - нечетности функции не говорим, если (ее область определения не симметрична относительно нуля).
-
Производная функции (х-3)1 равна (-3*х-4).
-
Производная функции (е2*х)1 равна (2*е2*х).
-
Если функция положительна, то ее график (расположен выше оси Ох).
-
Укажите область определения функции y=
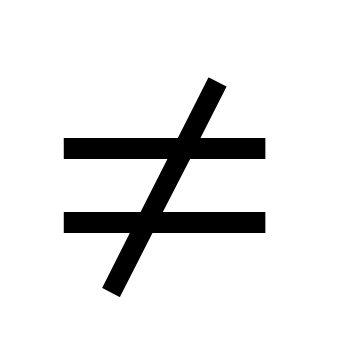 (x
(x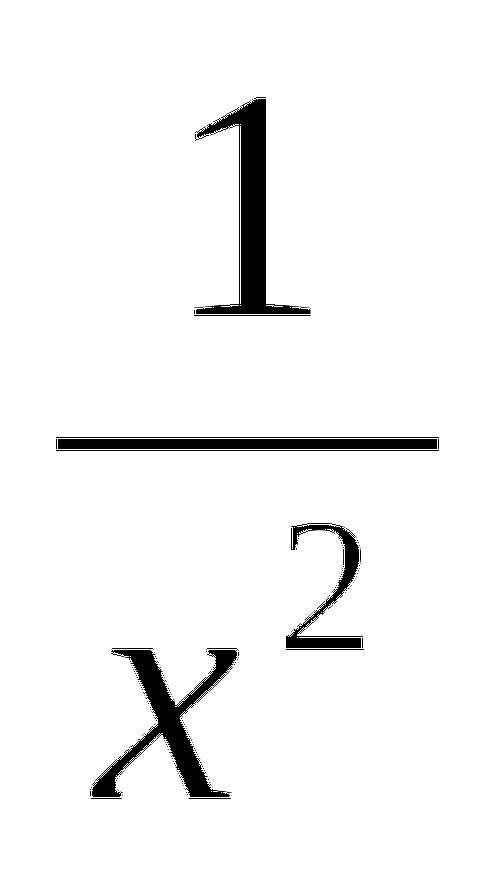 2).
2). -
Асимптота графика функции - это прямая, (которую график функции не пересекает).
-
Если при переходе через стационарную точку производная не меняет свой знак, то эта точка (не является экстремумом функции).
-
Производная функции (6*х-6)1 равна (6).
-
Производная функции (
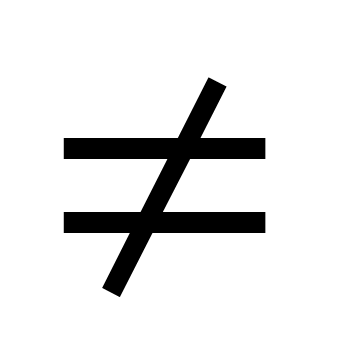 )1 равна (0).
)1 равна (0). -
Производная функции (
 )1 равна (
)1 равна (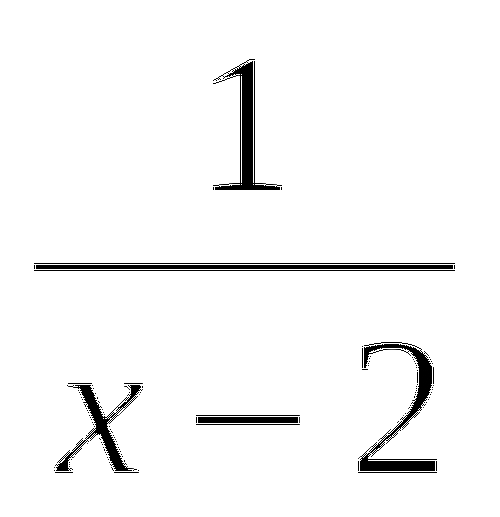 ).
).
Приложение 4
Найди пару
X5
1
Х
2
2*X
3
1
4
2
5
X-3
6
![]()
7
SIN X
8
5*X4
9
-3*X-4
10
![]()
11
-3
12
-SIN X
13
![]()
14
A*X
15
A
16
COS X
17
![]()
18
0
19
12*X-5
20ВАРИАНТ А
X7
1
7*Х6
2
-3
3
![]()
4
-4*x-5
5
0
6
2*SIN X
7
X
8
-3*X
9
2*COS X
10
![]()
11
42*X5
12
X-4
13
![]()
14
- 2*COS X
15
20*X-6
16
![]()
17
-2*SIN X
18
![]()
19
1
20ВАРИАНТ Б
Ключи к заданию.
Вариант А Вариант Б
1-9 1-2
2-4 2-12
3-5 3-6
4-19 4-17
5-19 5-16
6-10 6-6
7-18 7-10
8-17 8-20
9-нет, 20*х3 9-3
10-20 10-18
11-14 11-14
12-19 12-нет, 210*х4
13-нет, -cosx 13-5
14- нет, 6*х-4 14-нет, 2*х -3
15-16 15-7
16-19 16-нет, -120*х -7
17-13 17-нет, -![]() = -
= -![]() *х -
*х -![]()
18-нет, -![]() =-
=-![]() *х-
*х-![]() 18-15
18-15
19-19 19-6
20-нет, -![]() =-60*х-6 20-6
=-60*х-6 20-6
Приложение 5
Вариант 1
-
По графику производной функции y=f'(x) определите, на каких промежутках функция y=f(x) возрастает, а на каких - убывает?
у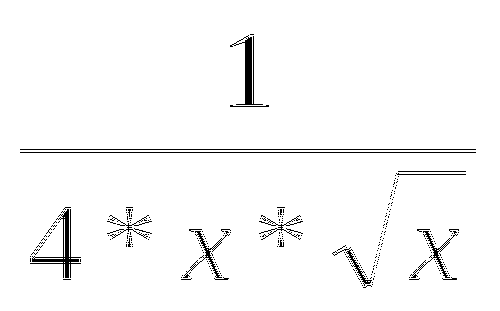
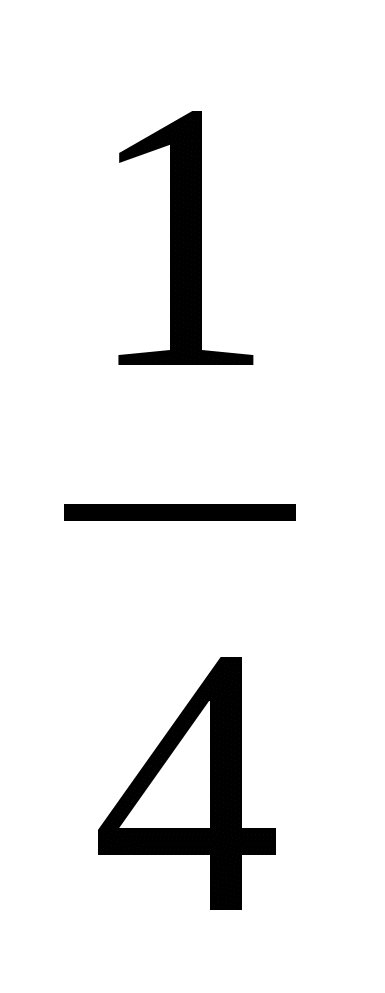 y=f1(x)
y=f1(x)
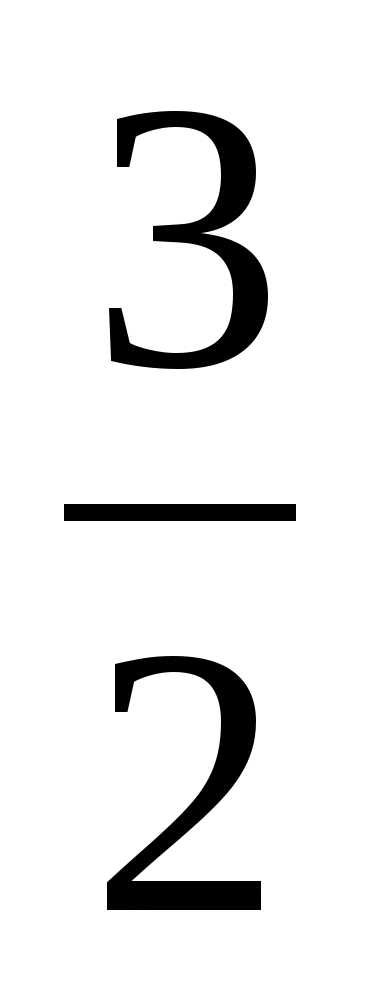 2
2
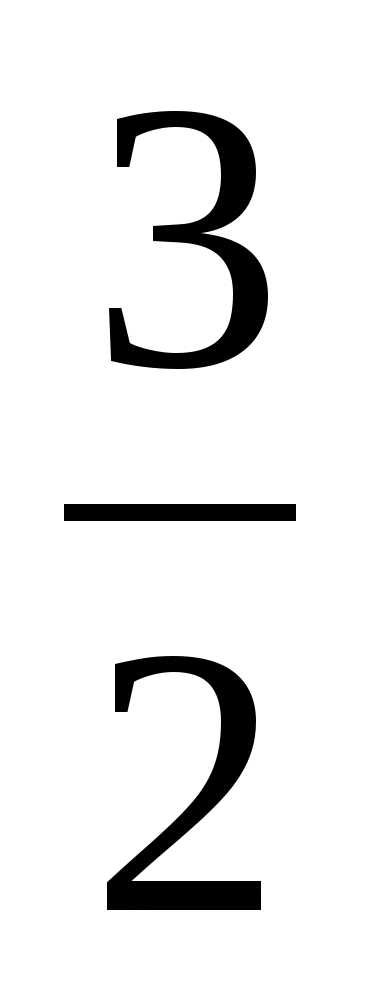 -4 -3 -1 1 4 х
-4 -3 -1 1 4 х
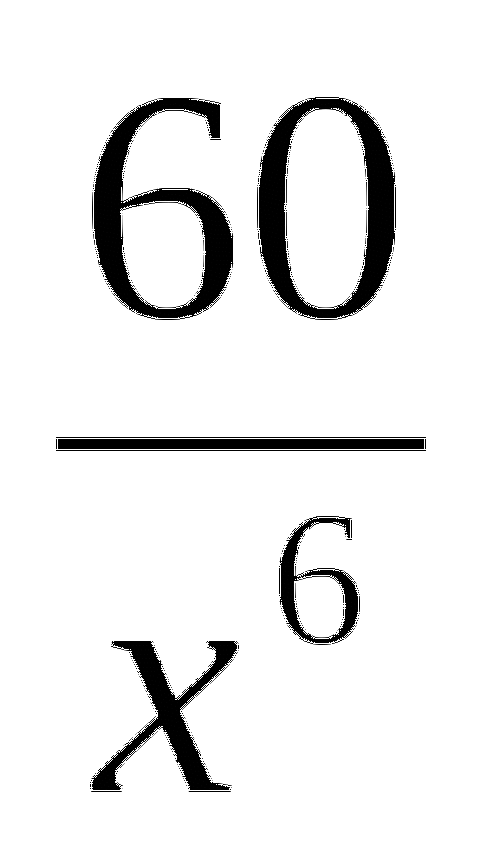






-
Схематично изобразите график функции y=g(x), исследование которой с помощью производной представлено в таблице:
x
(- ![]() ; -9)
; -9)
-9
( -9; 6 )
6
(6; + ![]() )
)
g'
+
0
-
0
+
g

5

-1

Вариант 2
-
По графику производной функции y=g'(x) определите, на каких промежутках функция y=g(x) возрастает, а на каких - убывает?
у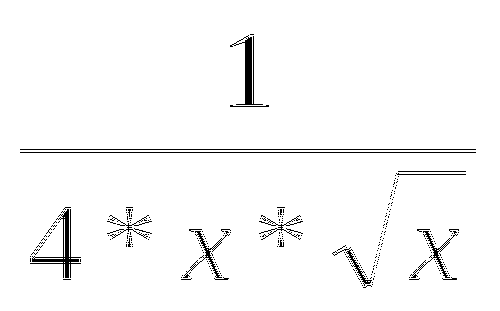

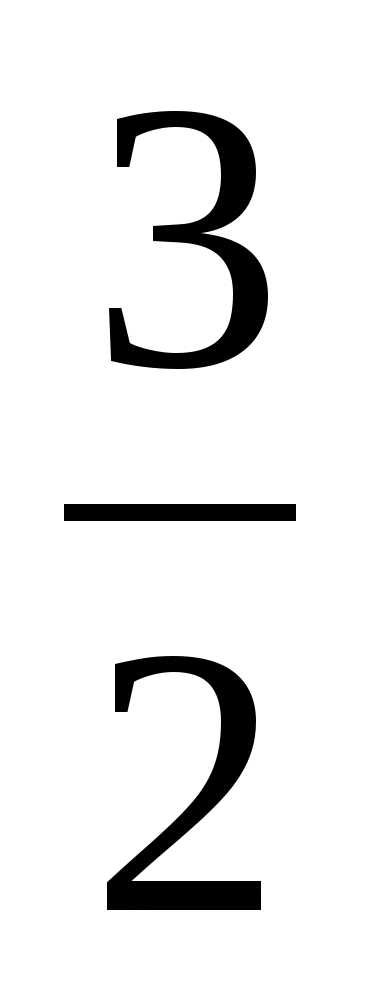 2 y=g1(x)
2 y=g1(x)
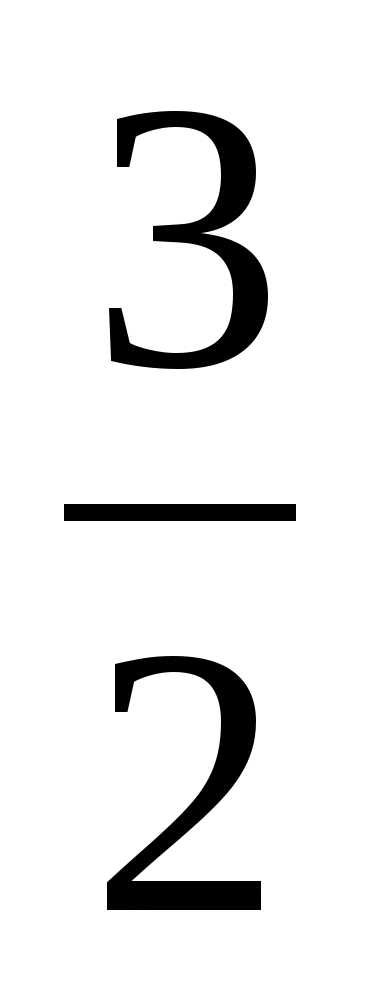 -4 -3 -1 1 4 х
-4 -3 -1 1 4 х
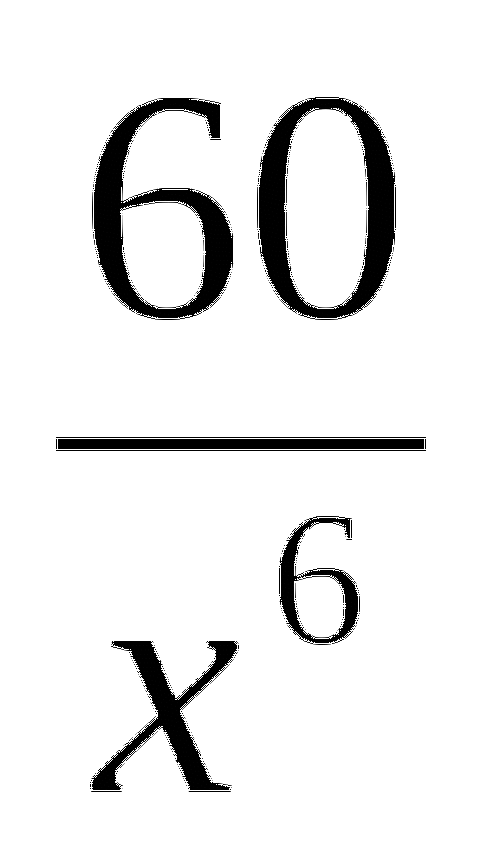






-
Схематично изобразите график функции y=f(x), исследование которой с помощью производной представлено в таблице:
x
(- ![]() ; -5)
; -5)
-5
( -5; 3 )
3
(3; + ![]() )
)
f'
-
0
+
0
-
f

-5

-1

Ключ к заданию.
Вариант 1
-
у=f(x) : возрастает при х<- 4; -2<x<4;
убывает при -4<x<-2; x>4.
2
 . у
. у
 5
5


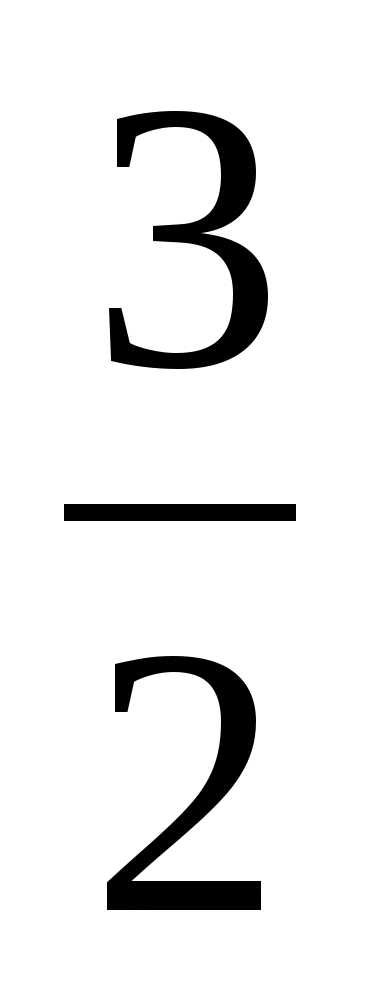 2
2



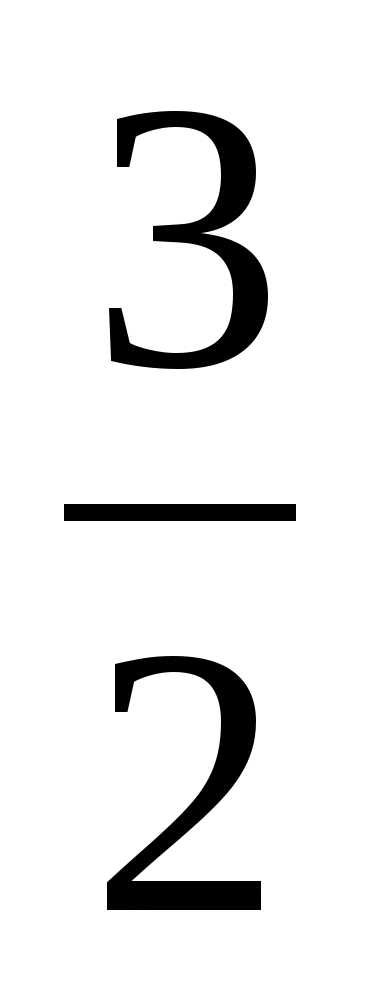



 -9 -4 -3 -1 1 4 х
-9 -4 -3 -1 1 4 х






Вариант 2
-
у=f(x) : возрастает при х>1,8 ; -5<x<-1;
убывает при -1<x<1,8; x<-5.

2. у
 5
5


 2
2






 -9 -4 -3 -1 1 4 х
-9 -4 -3 -1 1 4 х






Приложение 6
Шарада (в ней требуется отгадать определенное слово. Каждое слово отгадывается не все сразу, а по частям).
Предлоги малое число,
За ними букву скажем.
А в целом - ты найдешь его
Почти под домом каждым. (по-два-л)
Метаграмма( в ней зашифровано определенное слово. Его нужно отгадать. Затем, в расшифрованном слове следует одну из указанных букв заменить другой буквой, и значение слова изменится).
Я приношу с собою боль,
В лице большое искажение,
А «Ф» на «П» заменишь коль,
То превращаюсь в знак сложения. (флюс-плюс)
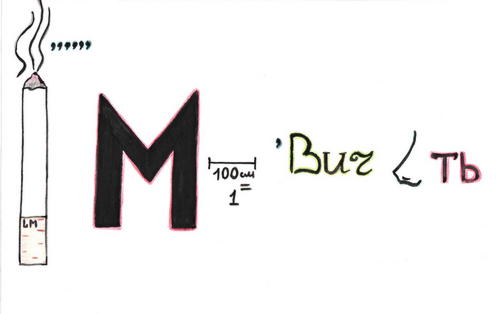 Ребусы
Ребусы
Ответ: Симметричность.
Ответ: Максимум.
Ответ: Экстремум.

Ответ: Аргумент.

Ответ: Производная.

Ответ: Аргумент.
 Ответ: Монотонность.
Ответ: Монотонность.

Ответ: График.
Ответ: Приращение.

Ответ: Первообразная.
Кроссворд № 1

Ответы: 1. Экстремумы. 2. Дифференциал. 3. Критические. 4. Предел. 5. Чётная.
6. Монотонность. 7. Приращение. 8. Производная. 9. Максимума. 10. Возрастание.
Кроссворд № 2
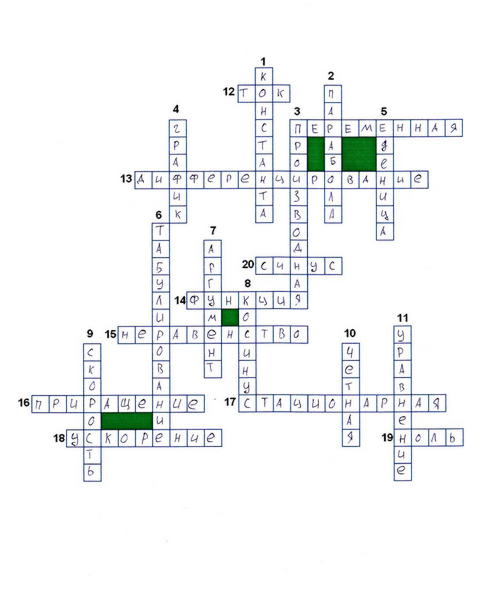

Кроссворд № 3
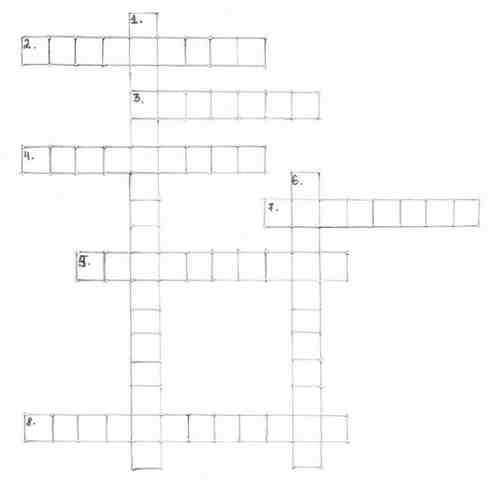


1. Дифференцирование. 2. …максимума. 3. Функция. 4. Экстремма (экстремум).
5. Приращение. 6. Производная. 7. Аргумент. 8. Стационарная.
Кроссворд № 4

Кроссворд № 5
Найдите зашифрованное слово.
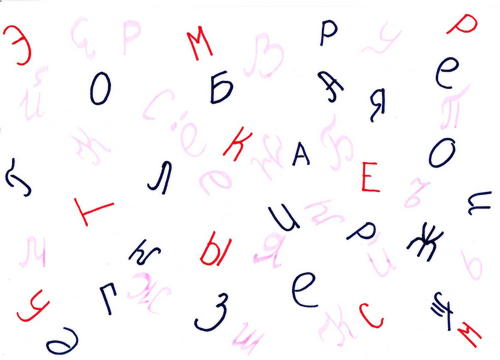
Ответ: Экстремумы.
Кроссворд № 6 (шифрограмма)
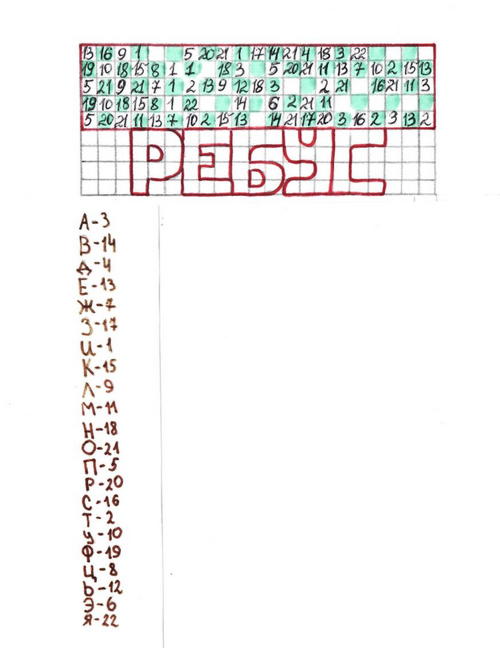
Ответ: Если производная функции на промежутке положительна, то сама функция на этом промежутке возрастает.